目錄
激活函數
1. Sigmoid
2. Tanh 函數(雙曲正切)
3. ReLU 函數
4. Leaky ReLU (LReLU)
5. Softmax
總結對比表
損失函數選擇
激活函數
激活函數是神經網絡中每個神經元(節點)的核心組成部分。它接收上一層所有輸入的加權和(加上偏置項),并產生該神經元的輸出。其主要作用是引入非線性,使得神經網絡能夠學習和逼近任意復雜的函數關系。如果沒有非線性激活函數,無論網絡有多少層,最終都等價于一個線性變換(單層感知機),能力極其有限。
1. Sigmoid
-
公式:
-
原理: 將輸入壓縮到
(0, 1)區間。輸出值可以被解釋為概率(尤其是在二分類問題的輸出層)。它平滑、易于求導。 -
特征:
-
輸出范圍: (0, 1)
-
單調遞增: 函數值隨輸入增大而增大。
-
S型曲線: 中間近似線性,兩端飽和(變化緩慢)。
-
導數:
????????最大值為0.25(當x=0時)。
-
-
缺點:
-
梯度消失: 當輸入
x的絕對值很大時(處于飽和區),導數σ'(x)趨近于0。在反向傳播過程中,梯度會逐層連乘這些接近0的小數,導致深層網絡的梯度變得非常小甚至消失,使得網絡難以訓練(權重更新緩慢或停滯)。 -
信息丟失:輸入100和輸入10000經過sigmoid的激活值幾乎都是等于 1 的,但是輸入的數據卻相差 100 倍。
-
輸出非零中心化: 輸出值始終大于0。這可能導致后續層的輸入全為正(或全為負),使得權重更新時梯度全部朝同一方向(正或負)移動,降低收斂效率(呈“之”字形下降路徑)。
-
計算相對較慢: 涉及指數運算。
-
-
函數繪制:
-
當
x -> -∞時,σ(x) -> 0(左水平漸近線 y=0)。 -
當
x = 0時,σ(0) = 0.5。 -
當
x -> +∞時,σ(x) -> 1(右水平漸近線 y=1)。 -
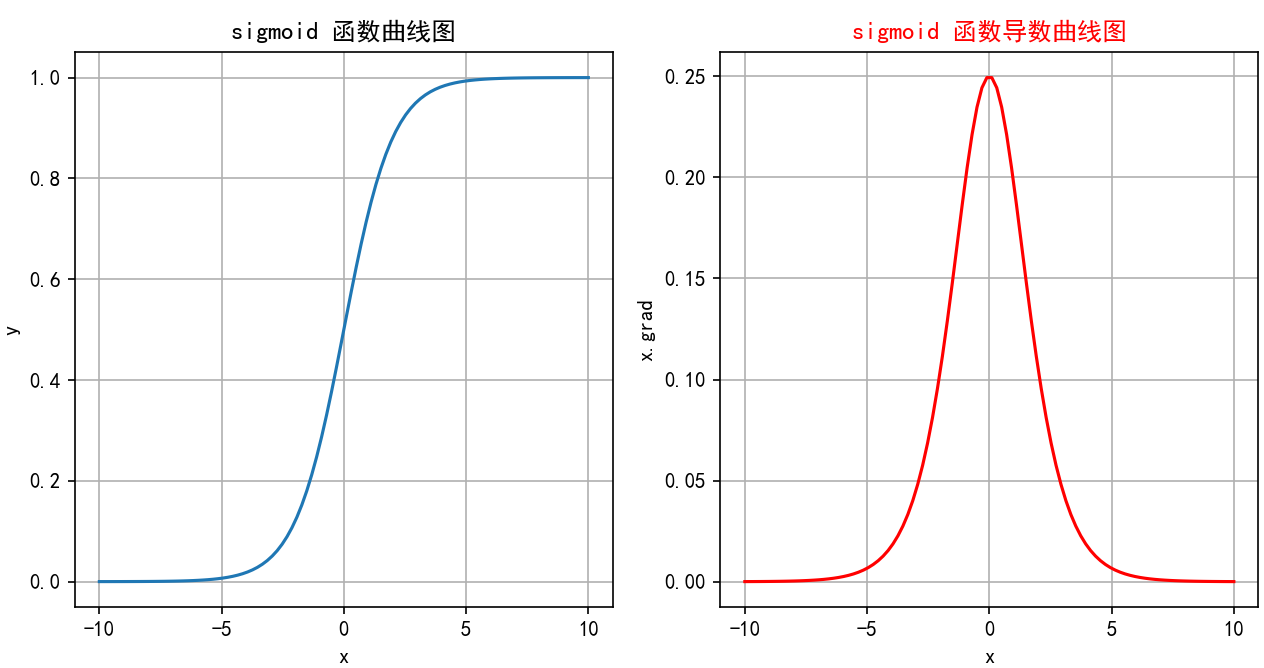
圖像是一條平滑的、從接近0上升到接近1的S形曲線,關于點(0, 0.5)中心對稱。導數曲線是一個鐘形曲線,在x=0處達到峰值0.25,向兩邊迅速衰減到0。
-
2. Tanh 函數(雙曲正切)
-
公式:
-
原理: 將輸入壓縮到
(-1, 1)區間。是Sigmoid函數的縮放和平移版本。解決了 Sigmoid 輸出均值非零的問題,更適合作為隱藏層激活函數。 -
特征:
-
輸出范圍: (-1, 1)
-
單調遞增: 函數值隨輸入增大而增大。
-
S型曲線: 中間近似線性,兩端飽和。
-
零中心化: 輸出關于原點對稱(
tanh(-x) = -tanh(x))。這是相比于Sigmoid的主要優勢,通常能使后續層的輸入具有更理想的均值,有助于加速收斂。 -
導數:
tanh'(x) = 1 - tanh2(x),最大值為1(當x=0時)。
-
-
缺點:
-
梯度消失: 和Sigmoid類似,當
|x|很大時,導數趨近于0,仍然存在梯度消失問題(雖然比Sigmoid稍好,因為其導數值更大)。 -
計算相對較慢: 同樣涉及指數運算。
-
-
函數繪制:
-
當
x -> -∞時,tanh(x) -> -1(左水平漸近線 y=-1)。 -
當
x = 0時,tanh(0) = 0。 -
當
x -> +∞時,tanh(x) -> 1(右水平漸近線 y=1)。 -
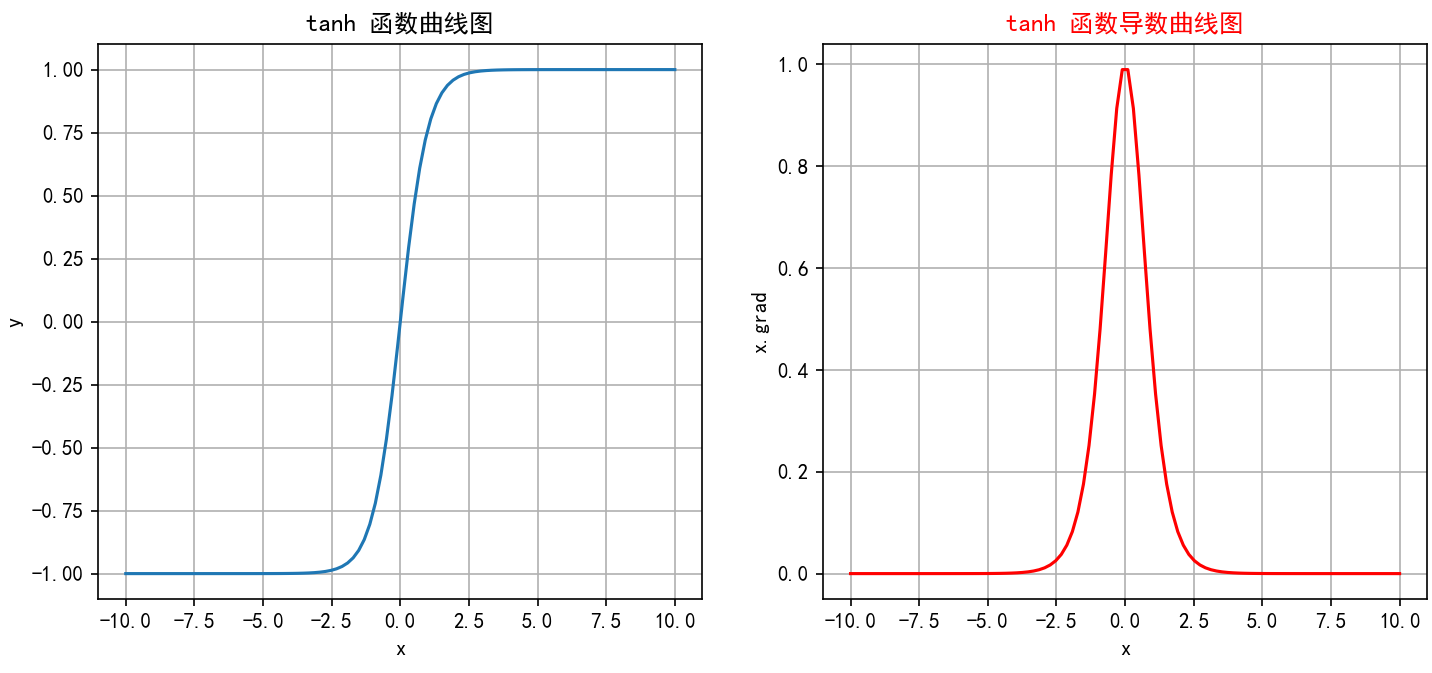
圖像是一條平滑的、從接近-1上升到接近1的S形曲線,關于原點(0,0)中心對稱。導數曲線是一個鐘形曲線,在x=0處達到峰值1,向兩邊衰減到0。整體形狀比Sigmoid更陡峭,飽和區變化更快。
-
3. ReLU 函數
-
公式:
-
原理: ReLU 是目前最常用的隱藏層激活函數之一,通過簡單的線性分段
-
特征:
-
輸出范圍: [0, +∞)
-
計算極其高效: 只需比較和取最大值操作,沒有指數等復雜運算。
-
緩解梯度消失: 在正區間 (
x > 0),導數為1,梯度可以無損地反向傳播,有效緩解了梯度消失問題,使得深層網絡訓練成為可能。這是其成功的關鍵。 -
ReLU 函數的導數是分段函數:
-
生物學合理性: 更接近生物神經元的稀疏激活特性(只有一部分神經元被激活)。
-
稀疏激活:
? 時輸出為 0,使網絡具有 “稀疏性”(僅部分神經元激活),模擬生物神經元的工作模式。
-
-
缺點:
-
死亡ReLU (Dying ReLU): 在負區間 (
x < 0),導數為0。如果一個神經元的加權和輸入在訓練過程中大部分時間都小于0(例如,學習率過高或負的偏置過大),那么它的梯度在反向傳播時始終為0,導致該神經元的權重無法再更新,永遠“死亡”(輸出恒為0,不再參與訓練)。 -
輸出非零中心化: 輸出始終 >= 0。
-
在
x=0處不可導: 實踐中通常將x=0處的導數設為0或1(通常設為0)。
-
-
函數繪制:
-
當
x < 0時,ReLU(x) = 0(沿x軸負半軸)。 -
當
x >= 0時,ReLU(x) = x(沿y=x直線在第一象限)。 -
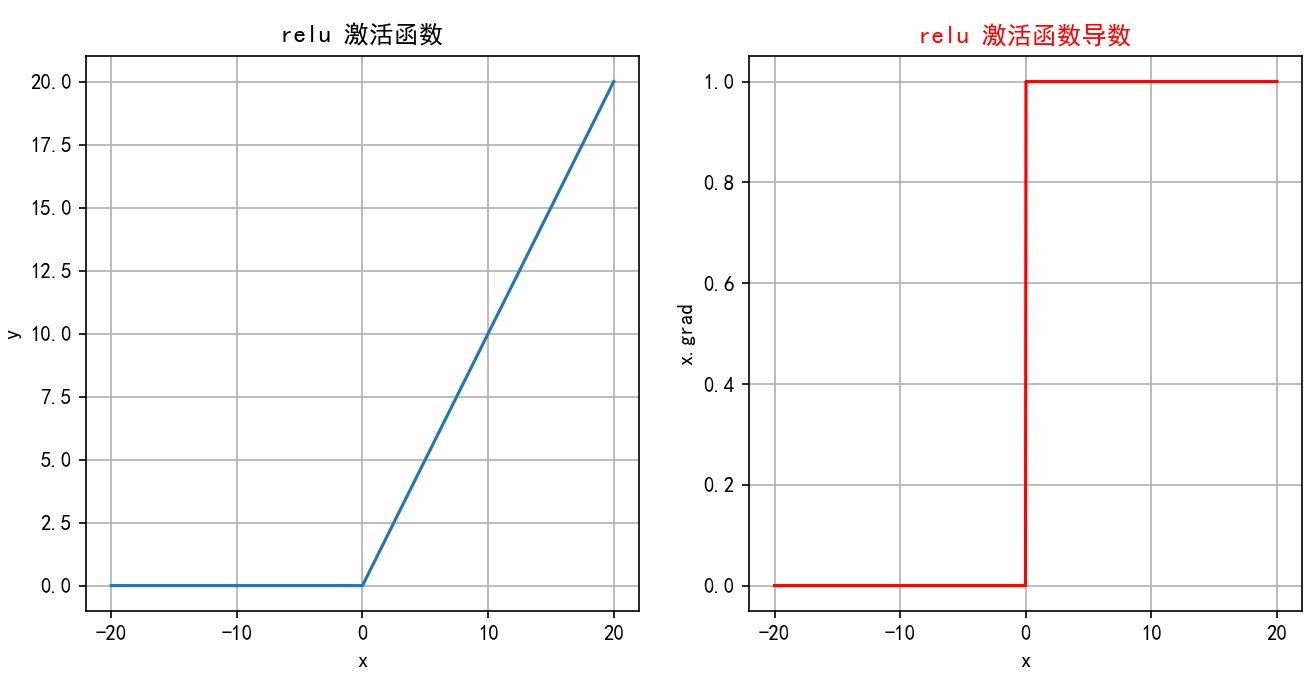
圖像是一個簡單的折線:在原點(0,0)左側是水平線(y=0),在原點右側是一條45度角的直線(y=x)。導數圖像:在x<0處是y=0的水平線;在x>0處是y=1的水平線;在x=0處不連續(通常畫一個空心點)。
-
4. Leaky ReLU (LReLU)
-
公式:
?(其中
α是一個很小的正數常數,如0.01) -
原理: 針對標準ReLU的“死亡”問題進行的改進。在負區間給予一個很小的非零斜率
α。 -
特征:
-
輸出范圍: (-∞, +∞) (理論上,但負值部分很小)
-
緩解死亡ReLU: 在負區間有小的梯度
α,(x<0)時輸出(\alpha x)(非零),即使輸入為負,神經元也有機會更新權重,避免了永久性“死亡”。 -
計算高效: 和ReLU一樣高效。
-
-
缺點:
-
效果依賴
α: 需要人工設定或嘗試α值。雖然通常設0.01有效,但并非最優。 -
在
x=0處不可導: 同樣的問題。 -
負區間表現可能不一致: 微小的負斜率可能不足以完全解決某些場景下的問題,或者引入不必要的復雜性。
-
-
函數繪制:
-
當
x >= 0時,LReLU(x) = x(沿y=x直線在第一象限)。 -
當
x < 0時,LReLU(x) = αx(一條斜率為α的直線,在第三象限,非常平緩)。 -
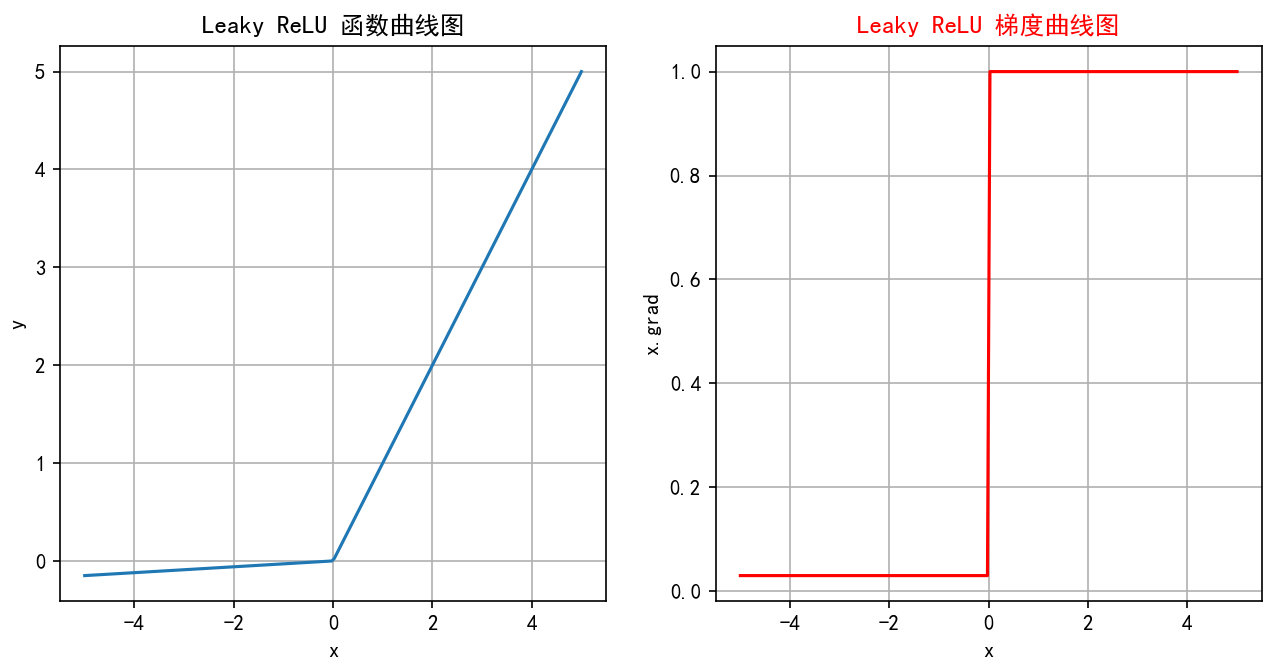
圖像在原點右側與ReLU相同(y=x),在原點左側是一條斜率很小(接近水平)的直線。導數圖像:在x>0處是y=1的水平線;在x<0處是y=α的水平線(非常接近0);在x=0處不連續。
-
5. Softmax
-
公式:??????????????
?(其中
是第i個神經元的輸入,K是輸出層神經元的個數/類別數)
給定輸入向量 z=[
,
,…,
]
1.指數變換:對每個?
?進行指數變換,得到
,使z的取值區間從
? 變為??
2.將所有指數變換后的值求和,得到
3.將t中每個
?除以歸一化因子s,得到概率分布:
?即:????????
? -
原理: 將多個神經元的輸入(通常是一個向量
z = [z1, z2, ..., zK])轉換為一個概率分布。每個輸出值在(0, 1)區間,且所有輸出值之和為1,適合作為多分類任務的輸出層。 -
特征:
-
輸出范圍: (0, 1)
-
歸一化: 輸出總和為1,非常適合表示K個互斥類別的概率分布(多分類問題)。
-
放大差異: 輸入值中最大的那個,其對應的輸出概率會被顯著放大(指數效應),較小的輸入對應的概率會被壓縮。
-
在實際應用中,Softmax常與交叉熵損失函數Cross-Entropy Loss結合使用,用于多分類問題。在反向傳播中,Softmax的導數計算是必需的。
-
-
缺點:
-
僅用于輸出層: 通常只在多分類網絡的最后一層使用。
-
梯度消失:當某個輸入遠大于其他時,其對應的輸出趨近于 1,其他趨近于 0,梯度接近 0。
-
API
torch.nn.functional.softmax
import torch
import torch.nn as nn
?
# 表示4分類,每個樣本全連接后得到4個得分,下面示例模擬的是兩個樣本的得分
input_tensor = torch.tensor([[-1.0, 2.0, -3.0, 4.0], [-2, 3, -3, 9]])
?
softmax = nn.Softmax()
output_tensor = softmax(input_tensor)
# 關閉科學計數法
torch.set_printoptions(sci_mode=False)
print("輸入張量:", input_tensor)
print("輸出張量:", output_tensor)?
輸出結果:
輸入張量: tensor([[-1., ?2., -3., ?4.],[-2., ?3., -3., ?9.]])
輸出張量: tensor([[ ? ?0.0059, ? ? 0.1184, ? ? 0.0008, ? ? 0.8749],[ ? ?0.0000, ? ? 0.0025, ? ? 0.0000, ? ? 0.9975]])總結對比表
| 激活函數 | 公式 | 輸出范圍 | 優點 | 缺點 | 適用場景 | 函數繪制描述 |
|---|---|---|---|---|---|---|
| Sigmoid | (0, 1) | 平滑,輸出可解釋為概率,導數易求 | 梯度消失嚴重,輸出非零中心,計算慢 | 二分類輸出層,早期隱藏層 | S形曲線,從(0,0)附近到(0,1)附近,關于(0,0.5)對稱 | |
| Tanh | (-1, 1) | 零中心化,梯度比Sigmoid稍大 | 仍有梯度消失,計算慢 | 隱藏層(比Sigmoid更常用) | S形曲線,從(0,-1)附近到(0,1)附近,關于(0,0)對稱 | |
| ReLU | max(0, x) | [0, +∞) | 計算極快,有效緩解梯度消失(正區間),生物學啟發,實踐效果好 | 死亡ReLU問題,輸出非零中心,x=0不可導 | 最常用隱藏層 (CNN, FNN) | x<0為水平線(y=0),x>=0為45度線(y=x),原點處轉折 |
| Leaky ReLU | | (-∞, +∞) | 緩解死亡ReLU,計算快 | 效果依賴α,x=0不可導,負斜率可能非最優 | 隱藏層 (ReLU的改進嘗試) | x>=0同ReLU(y=x),x<0為斜率很小的直線(y=αx) |
| Softmax | (0, 1), Σ=1 | 輸出歸一化為概率分布,適合多分類 | 僅用于輸出層,數值不穩定(需技巧) | 多分類輸出層 | 作用于向量,輸出概率向量。最大輸入對應最大概率(接近1) |
損失函數選擇
-
隱藏層:優先用ReLU,計算快、效果穩。若出現大量 “死神經元”(輸出恒為 0),換Leaky ReLU
-
輸出層:
-
二分類: Sigmoid (輸出單個概率)。
-
多分類: Softmax (輸出類別概率分布)。
-
回歸:
-
輸出非負(如銷量):ReLU
-
輸出可正可負(如溫度):線性激活(y=x) 或Tanh(配合縮放)
-
-
循環網絡(RNN/LSTM):門控用Sigmoid(控制開關),狀態用Tanh(限制范圍)。
-
-
避免使用: 在深度網絡的隱藏層中,通常避免使用Sigmoid(梯度消失問題嚴重),也較少使用原始Tanh(ReLU族通常更優)。

)












)




