前言
我發現在csdn寫完一篇文章越來越難了,有n篇寫了一半沒往下寫。原來我覺得補完203篇,湊到一千篇是個很簡單的事,沒想到還挺難的。
我回想了一下,過去一年大模型領域繼續發生這很劇烈的變化,這是一種新的模式 ,和原來慢慢寫一篇技術文章其實是沖突的。而我在過去一年里,半是因為工作的壓力,不得不去適應;另一半則是我也認同這種變化,正在適應和遷移。
寫文檔的本質是梳理自己的知識,并進行傳播。
但是大模型太強了,隨之產生的一系列生態使得再去慢慢寫文章顯得奢侈和過時。我覺得我還是會補完剩下的170篇的,但是進度可能會慢一些。而且更多的是關于算法領域的,這方面大模型還差很遠,我暫時不會和大模型協同。過去的什么工具部署、使用啥的,我覺得個人已經完全沒有必要那么詳細的去寫細節,而是去了解原理。
下面的文字部分全部手打,代碼部分逐行掃過,所以說起來是挺奢侈的。(現在一般是讓大模型寫,然后測一下,給個報告)
強化學習
介紹啥的也不想說了,反正大模型都懂。這是我覺得非常關鍵的一步,但遲遲不得門而入。
所以先從QLearning開始,QLearning又從gym開始。這個項目最初是openai做的,當時的確挺open的。
下面這段代碼是基于平衡車做的一個基準版本。env代表了環境,env的step方法會對每次的action作出評估:
- 1 next_state : 表示執行了 action 之后,環境當前的新狀態。
- 2 reward: agent 執行該動作之后,環境給予的即時獎勵。
- 3 terminated: 指示該回合是否自然結束(如達到目標、失敗等)
- 4 truncated: 指示該回合是否被人為打斷(如超過最大步數、時間限制等)。
- 5 info :包含調試信息或額外狀態(例如獎勵結構分解、中間結果、原始 observation)。
下面做了一個特別簡單(機械)的方法,如果桿子向右傾斜,小車向右移動,如果桿子向左傾斜,則車子向左移動。
import gym# 創建環境(這里使用經典的 CartPole 平衡問題)
env = gym.make('CartPole-v1', render_mode='human') # render_mode='human' 表示可視化# 初始化環境,返回初始狀態
state, _ = env.reset()
print("初始狀態:", state)# 第一次執行隨機動作獲取初始狀態
action = env.action_space.sample()
next_state, reward, terminated, truncated, info = env.step(action)
print(f"Step 0: 動作={action}, 獎勵={reward}, 新狀態={next_state}")# 基于狀態的控制策略
for t in range(1, 200): # 最多運行 200 步# env.render() # 渲染當前環境(可視化)# 基于桿子角度的簡單控制策略if next_state[2] > 0: # 桿子向右傾斜action = 1 # 向右移動else: # 桿子向左傾斜action = 0 # 向左移動# 執行動作,返回:新狀態、獎勵、是否終止、額外信息next_state, reward, terminated, truncated, info = env.step(action)print(f"Step {t}: 動作={action}, 獎勵={reward}, 新狀態={next_state}")if terminated or truncated:print("Episode 結束!原因:")if abs(next_state[2]) > 0.2095: # 約12度(0.2095弧度)print(f"- 桿子傾斜角度過大: {next_state[2]:.4f} 弧度(約{next_state[2]*180/3.14159:.1f}度)")if abs(next_state[0]) > 2.4:print(f"- 小車超出邊界: 位置={next_state[0]:.4f}")break# 關閉環境
env.close()這種方法大概過不了關
初始狀態: (array([ 0.04398132, -0.01324874, 0.01681901, 0.01633218], dtype=float32), {})
Step 0: 動作=0, 獎勵=1.0, 新狀態=[ 0.04371634 -0.20860781 0.01714565 0.3142739 ]
Step 1: 動作=1, 獎勵=1.0, 新狀態=[ 0.03954419 -0.01373424 0.02343113 0.02704708]
Step 2: 動作=1, 獎勵=1.0, 新狀態=[ 0.0392695 0.181044 0.02397207 -0.25815195]
Step 3: 動作=1, 獎勵=1.0, 新狀態=[ 0.04289038 0.37581566 0.01880903 -0.5431784 ]
Step 4: 動作=1, 獎勵=1.0, 新狀態=[ 0.05040669 0.5706683 0.00794546 -0.8298761 ]
Step 5: 動作=1, 獎勵=1.0, 新狀態=[ 0.06182006 0.76568073 -0.00865206 -1.1200496 ]
Step 6: 動作=0, 獎勵=1.0, 新狀態=[ 0.07713367 0.57067335 -0.03105305 -0.83009315]
Step 7: 動作=0, 獎勵=1.0, 新狀態=[ 0.08854714 0.3759893 -0.04765491 -0.547336 ]
Step 8: 動作=0, 獎勵=1.0, 新狀態=[ 0.09606693 0.18156812 -0.05860163 -0.27004054]
Step 9: 動作=0, 獎勵=1.0, 新狀態=[ 0.09969829 -0.01267074 -0.06400245 0.00359858]
Step 10: 動作=0, 獎勵=1.0, 新狀態=[ 0.09944487 -0.20681919 -0.06393047 0.2754211 ]
Step 11: 動作=0, 獎勵=1.0, 新狀態=[ 0.09530849 -0.40097353 -0.05842205 0.54727495]
Step 12: 動作=0, 獎勵=1.0, 新狀態=[ 0.08728902 -0.59522814 -0.04747655 0.82099336]
Step 13: 動作=0, 獎勵=1.0, 新狀態=[ 0.07538446 -0.7896694 -0.03105668 1.0983738 ]
Step 14: 動作=0, 獎勵=1.0, 新狀態=[ 0.05959107 -0.98436904 -0.00908921 1.3811532 ]
Step 15: 動作=0, 獎勵=1.0, 新狀態=[ 0.03990369 -1.1793764 0.01853386 1.67098 ]
Step 16: 動作=1, 獎勵=1.0, 新狀態=[ 0.01631616 -0.9844746 0.05195345 1.3841261 ]
Step 17: 動作=1, 獎勵=1.0, 新狀態=[-0.00337333 -0.7900377 0.07963598 1.1081318 ]
Step 18: 動作=1, 獎勵=1.0, 新狀態=[-0.01917408 -0.5960475 0.10179861 0.84145695]
Step 19: 動作=1, 獎勵=1.0, 新狀態=[-0.03109504 -0.40245155 0.11862775 0.5824435 ]
Step 20: 動作=1, 獎勵=1.0, 新狀態=[-0.03914407 -0.20917389 0.13027662 0.32935935]
Step 21: 動作=1, 獎勵=1.0, 新狀態=[-0.04332754 -0.01612387 0.13686381 0.08043125]
Step 22: 動作=1, 獎勵=1.0, 新狀態=[-0.04365002 0.17679776 0.13847244 -0.16613266]
Step 23: 動作=1, 獎勵=1.0, 新狀態=[-0.04011406 0.3696939 0.13514978 -0.41212636]
Step 24: 動作=1, 獎勵=1.0, 新狀態=[-0.03272019 0.56266713 0.12690726 -0.65933347]
Step 25: 動作=1, 獎勵=1.0, 新狀態=[-0.02146685 0.7558158 0.11372058 -0.90951586]
Step 26: 動作=1, 獎勵=1.0, 新狀態=[-0.00635053 0.9492302 0.09553026 -1.1644017 ]
Step 27: 動作=1, 獎勵=1.0, 新狀態=[ 0.01263408 1.1429876 0.07224223 -1.4256694 ]
Step 28: 動作=1, 獎勵=1.0, 新狀態=[ 0.03549383 1.3371462 0.04372884 -1.694927 ]
Step 29: 動作=1, 獎勵=1.0, 新狀態=[ 0.06223675 1.5317371 0.0098303 -1.9736822 ]
Step 30: 動作=1, 獎勵=1.0, 新狀態=[ 0.09287149 1.7267541 -0.02964334 -2.2633033 ]
Step 31: 動作=0, 獎勵=1.0, 新狀態=[ 0.12740658 1.5319214 -0.0749094 -1.9798967 ]
Step 32: 動作=0, 獎勵=1.0, 新狀態=[ 0.15804501 1.3376632 -0.11450734 -1.7113292 ]
Step 33: 動作=0, 獎勵=1.0, 新狀態=[ 0.18479827 1.1440276 -0.14873391 -1.4563696 ]
Step 34: 動作=0, 獎勵=1.0, 新狀態=[ 0.20767882 0.9510109 -0.17786132 -1.2136078 ]
Step 35: 動作=0, 獎勵=1.0, 新狀態=[ 0.22669904 0.7585728 -0.20213346 -0.98152035]
Step 36: 動作=0, 獎勵=1.0, 新狀態=[ 0.2418705 0.5666487 -0.22176388 -0.7585189 ]
Episode 結束!原因:
- 桿子傾斜角度過大: -0.2218 弧度(約-12.7度)
| 條件 | 是否成功 |
|---|---|
| 支撐 500 步未失敗 | ? 是 |
| 中途桿倒或越界 | ? 否 |
使用QLearning 解決問題
結果:
...
Episode 19800: Total Reward = 366.0
Episode 19900: Total Reward = 1754.0
Episode 20000: Total Reward = 447.0
...
Step 480:
狀態: 位置=-0.19, 速度=-0.03, 角度=-4.9度, 角速度=-0.03
動作: 左
----------------------------
Step 490:
狀態: 位置=-0.21, 速度=-0.41, 角度=-4.9度, 角速度=0.29
動作: 左
----------------------------
Step 500:
狀態: 位置=-0.31, 速度=-0.40, 角度=-0.9度, 角速度=0.13
動作: 右
----------------------------
最終結果: 平衡了 500 步
成功達到500步最大限制!
對代碼進行一些剖析:
- 1 QLearning是一種離散化方法,而當前的狀態數據是連續的(比如速度、角度)
用minmax方法以及指定的格子,將連續值分為若干離散狀態。這種方法效率比較低,最后我會試圖用矩陣計算方法改進一下。
# 離散化連續狀態空間
def discretize_state(state, bins):discretized = []for i in range(len(state)):scale = (state[i] + abs(low[i])) / (high[i] - low[i])discretized.append(int(np.clip(scale * bins[i], 0, bins[i]-1)))return tuple(discretized)
環境中的狀態可以這樣獲取(另外,數據規整化的第一步的確是映射為數值)
env = gym.make('CartPole-v1')
state = env.reset()[0]'''
獲取到當前的環境的向量
array([-0.01736587, -0.04907 , -0.00341747, -0.01198332], dtype=float32)
'''
- 2 qtable的建立
QLearning的核心是QTable, QTable記錄了狀態 ~ 行動 ~ 價值的關聯。因為名字叫Table,我也就老是想著普通的table格式。邏輯上當然沒問題,
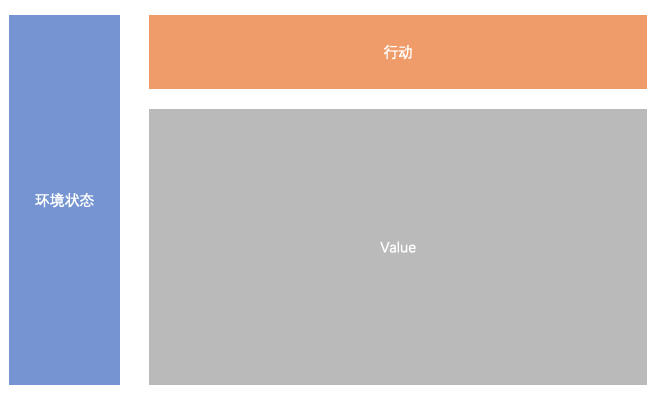
但實際上在這次探索時,我發現用tensor來記錄這個表的方式更科學。
上面的表可以按下面的方式定義,其中bins列表是每個維度的離散化箱體。
# 初始化Q表
bins = [2, 2, 2, 2] # 切少一點一點,可以觀察q表
q_table = np.zeros(bins + [env.action_space.n])
此時,qtable可以想象為一個高維空間,容納了每一種可能性。這個高維空間的構造方式,則是按照每個維度的箱體數量,構造一個嚴格MECE的高維表,每個空間都有一個值。
所以上面環境狀態和行動被歸一化為了「維度」,這些維度都對應了一個「值」。這對于進一步走向底層研究還是比較好的,比如QKV,這些都采用Tensor的方式。雖然很早就知道了Tensor的概念,但是我一直用高維矩陣的方式去理解,在業務意義上立即還是不夠。
下面的訓練過程中,也就是在不斷迭代qtable的過程。
# Q-learning訓練
for episode in range(episodes):state = env.reset()[0]discretized_state = discretize_state(state, bins)done = Falsetotal_reward = 0while not done:# ε-greedy策略if np.random.random() < epsilon:action = env.action_space.sample()else:action = np.argmax(q_table[discretized_state])next_state, reward, done, _, _ = env.step(action)total_reward += rewarddiscretized_next_state = discretize_state(next_state, bins)# Q-learning更新current_q = q_table[discretized_state + (action,)]max_next_q = np.max(q_table[discretized_next_state])new_q = (1 - alpha) * current_q + alpha * (reward + gamma * max_next_q)q_table[discretized_state + (action,)] = new_q# 狀態更新discretized_state = discretized_next_state# 打印每個回合的訓練信息if (episode + 1) % 100 == 0:log_str = f"Episode {episode+1}: Total Reward = {total_reward}\n"print(log_str, end="")log_file.write(log_str)
原理上說:
- 1 每個回合,通過隨機,或者歷史經驗,獲取當前狀態下將要采取的行動
- 2 采取改行動,獲取下一步的狀態,獎勵,同時也要觀察是否出現出現終止信號
- 3 根據貝爾曼方程,更新當前q值
- 4 將下一個狀態離散化,然后開始下一次循環
技術細節上,
- 1 找最好的行動
action = np.argmax(q_table[discretized_state]) 這個是把前面的維度都鎖住,只留下"行動"的column,然后通過argmax方法找出最大使得值最大的動作。如果動作不止是一列,也是一組值呢?按照目前的框架,恐怕也是要映射到一列上才行。
- 2 檢索當前的Q值
current_q = q_table[discretized_state + (action,)]
- 3 更新Q值
new_q = (1 - alpha) * current_q + alpha * (reward + gamma * max_next_q)
- 4 狀態更新
discretized_state = discretized_next_state
對離散化方法進行一些改進
import numpy as npdef discretize_state_batch(states: np.ndarray, bins: List[int], low: np.ndarray, high: np.ndarray) -> np.ndarray:"""將一個批量的狀態數組進行向量化離散化。參數:states: np.ndarray of shape (N, D),N 個狀態,每個狀態 D 維。bins: List[int],每一維要分多少個桶。low, high: 分別是每個維度的最小值和最大值(用于縮放)。返回:np.ndarray of shape (N, D),每一行是離散化后的狀態。"""states = np.array(states, dtype=np.float32) # (N, D)bins = np.array(bins)low = np.array(low)high = np.array(high)# 歸一化到 [0, 1]scale = (states - low) / (high - low + 1e-8)scale = np.clip(scale, 0, 1)# 縮放到 [0, bins[i]-1],并轉 intdiscretized = (scale * bins).astype(int)discretized = np.clip(discretized, 0, bins - 1)return discretizedstate = np.array([[-0.017, -0.049, -0.003, -0.011]]) # shape (1, 4)
low = np.array([-2.4, -2.0, -0.21, -2.0])
high = np.array([2.4, 2.0, 0.21, 2.0])
bins = [6, 6, 12, 6]discrete = discretize_state_batch(state, bins, low, high)
print(discrete) # [[2 2 5 2]]總結
到這里,基本上把QLearning的路鋪好了,接下來就是開始結合實際的場景開始用熟。






--字符分類函數,字符轉換函數,strlen,strcpy,strcat函數的使用和模擬實現)
質數時間)


![[Windows]Postman-app官方歷史版本下載方法](http://pic.xiahunao.cn/[Windows]Postman-app官方歷史版本下載方法)








