DoRA詳解：從LoRA到權重分解的進化

DoRA??是一種用于??大語言模型（LLM）微調??的技術，全稱為 ??"Weight-Decomposed Low-Rank Adaptation"??（權重分解的低秩自適應）。它是對現有微調方法（如 ??LoRA??）的改進，旨在更高效地調整模型參數，同時減少計算資源消耗。

論文鏈接：https://arxiv.org/pdf/2402.09353

??1. 概括??

核心思想??：DoRA 通過??分解預訓練模型的權重矩陣??，將其拆分為??幅度（magnitude）??和??方向（direction）??兩部分，分別進行低秩（low-rank）調整。這種分解方式能更精細地控制參數更新，提升微調效果。
??與 LoRA 的關系??：
- ??LoRA（Low-Rank Adaptation）??：通過在原始權重旁添加低秩矩陣（而非直接修改權重）來微調模型，減少參數量。
- ??DoRA??：在 LoRA 基礎上引入??權重分解??，進一步優化參數更新的方向和幅度，提高訓練穩定性。

??2. 詳解

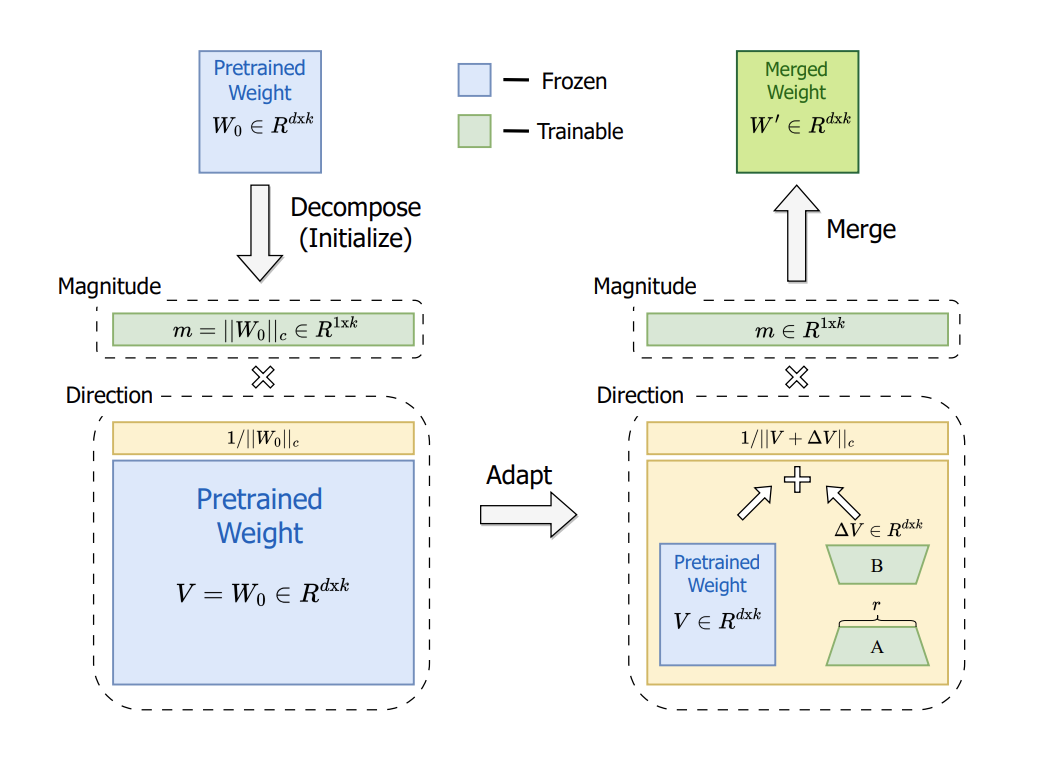
1. 權重矩陣分解

輸入與目標??

??輸入??：預訓練權重矩陣? $W_0\in \mathbb{R}^{d\times d}$ （藍色矩形）。
目標??：將 $W_0$ 分解為??幅度(Magnitude)? $m$ ?和??方向(Direction)? $V$ 。

?分解操作

1.1 計算幅度 $m$

$m=\left \| W_0 \right \|_c\in \mathbb{R}^{d\times d}$

$\left \| \cdot \right \|_c$ ?表示矩陣的 ??C范數??（具體可能是列范數或Frobenius范數，需根據上下文確定）。
幅度? $m$ ?是標量或對角矩陣（圖中淺綠色矩形），表示權重的整體縮放因子。

1.2?計算方向 $V$

$V=\frac{W_0}{\left \| W_0 \right \|_c}\in \mathbb{R}^{d\times d}$

方向（淺黃色矩形）是歸一化后的權重矩陣，保留原始權重的“方向”信息。

1.3?驗證分解??

重構公式：
說明：分解后可通過幅度和方向重新組合得到原始權重，確保數學等價性。
$V$ 的范數 $\left \| V \right \|_c=1$ （單位范數）。

2. 微調訓練

2.1 方向矩陣 $V$ 的低秩適應（LoRA）

低秩分解??
- 對方向矩陣應用標準 LoRA：
  - $\bigtriangleup V=BA\in \mathbb{R}^{d\times d}$
  - 其中 $A\in \mathbb{R}^{d \times r},B\in \mathbb{R}^{r\times d}, r\ll d$
- A和?B是??可訓練的低秩矩陣??（綠色矩形），r為秩（超參數）。
??更新方向矩陣??
- 微調后的方向矩陣：
  - $V'=V+\bigtriangleup V=V+BA$

?2.2 幅度 $m$ 的訓練?

幅度 $m$ 直接作為??可訓練參數??（綠色矩形），通過梯度下降調整。
- $W'=m\cdot \frac{V}{\left \| V \right \|_c}=m\cdot \frac{V+BA}{\left \| V+BA \right \|_c}$
- 通過歸一化確保方向矩陣的單位性。

??可訓練參數??：

低秩矩陣?A、B（方向調整）。

幅度?m（全局縮放調整）。

??凍結參數??：

原始方向?V（僅用于初始化，不更新）。

3. 代碼

偽代碼如下

import torch
import torch.nn as nnclass DoRALayer(nn.Module):def __init__(self, d, r):super().__init__()# 初始化預訓練權重 W0self.W0 = nn.Parameter(torch.randn(d, d))# 分解為幅度和方向self.m = nn.Parameter(torch.norm(self.W0, dim=0))  # 幅度（可訓練）self.V = self.W0 / torch.norm(self.W0, dim=0)      # 方向（凍結）# LoRA 參數self.A = nn.Parameter(torch.randn(d, r))self.B = nn.Parameter(torch.zeros(r, d))def forward(self, x):V_prime = self.V + torch.matmul(self.B, self.A)  # V + BAV_prime_norm = torch.norm(V_prime, dim=0)W_prime = self.m * (V_prime / V_prime_norm)       # 合并權重return torch.matmul(x, W_prime.T)

4. 總結?

DoRA 的核心是通過??權重分解 + 低秩適應??，實現對預訓練模型更精細的微調。其操作流程清晰分為兩步：

??分解??：提取權重的幅度和方向。
??微調??：用 LoRA 調整方向，獨立訓練幅度。

這種方法在保持參數效率的同時，提升了模型微調的靈活性和性能。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/pingmian/91316.shtml
繁體地址，請注明出處：http://hk.pswp.cn/pingmian/91316.shtml
英文地址，請注明出處：http://en.pswp.cn/pingmian/91316.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！