題目：最長回文子串

給你一個字符串 s，找到 s 中最長的 回文 子串。

示例 1：

輸入：s = “babad”
輸出：“bab”
解釋：“aba” 同樣是符合題意的答案。
示例 2：

輸入：s = “cbbd”
輸出：“bb”

提示：

1 <= s.length <= 1000
s 僅由數字和英文字母組成

思路：

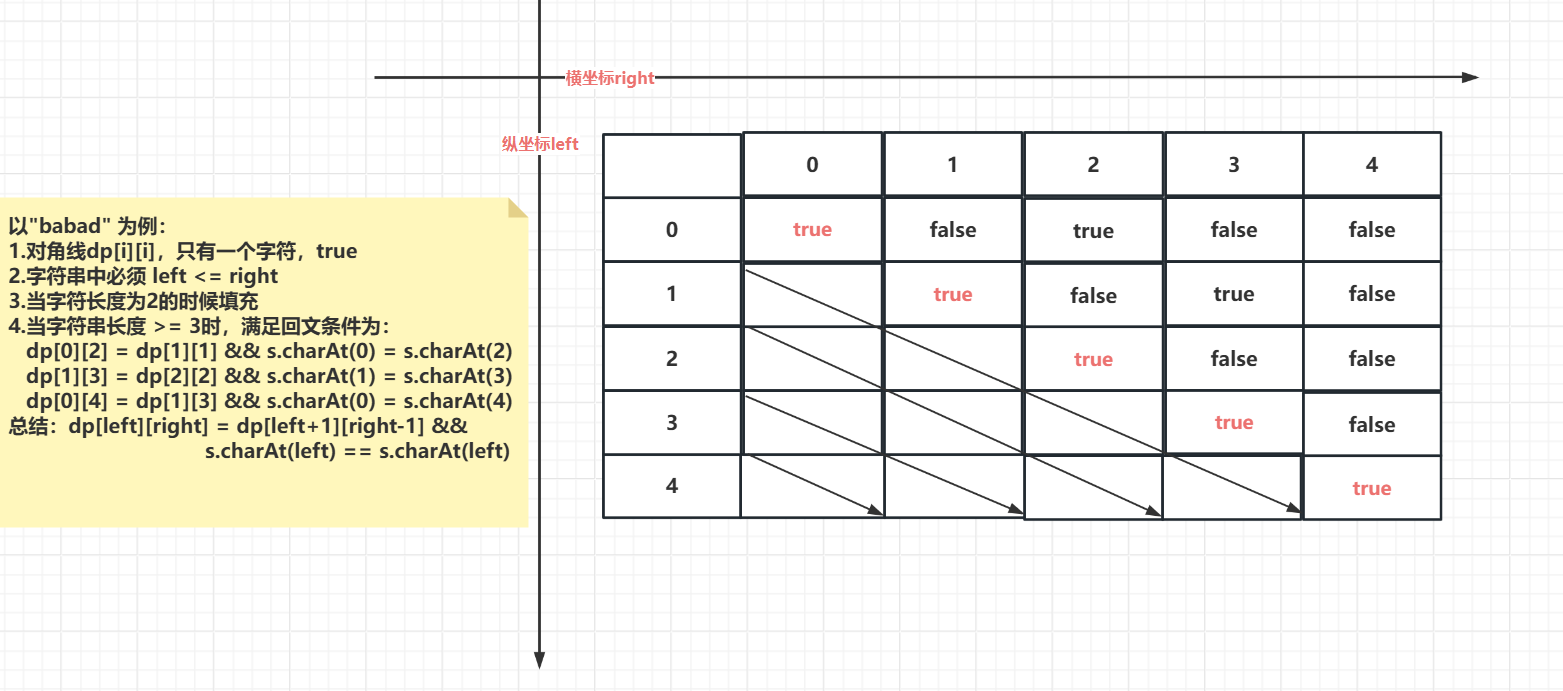
• 定義狀態：dp[i][j]表示字符串s從索引i到j的子串是否是回文
• 狀態轉移方程：
  如果s.charAt(i) == s.charAt(j)，那么dp[i][j] = dp[i+1][j-1]
  否則dp[i][j] = false
• 邊界條件：
  單個字符總是回文：dp[i][i] = true
  兩個相同字符也是回文：dp[i][i+1] = (s.charAt(i) == s.charAt(i+1))

題解：

1.普通遞歸實現（會超時）

//遞歸方式實現public static String longestPalindromic(String s){if(s == null || s.length() <= 1){return s;}int len = s.length();//判斷整個字符串是不是回文串if(isPalindrome(s, 0, len - 1)){return s;}// 遞歸檢查左子串和右子串String a = longestPalindromic(s.substring(1, len));String b = longestPalindromic(s.substring(0, len - 1));// 返回較長的那個子串return a.length() >= b.length() ? a : b;}// 輔助函數：檢查子串是否是回文public static Boolean isPalindrome(String s, int left, int right){if(left >= right){return true;}if(s.charAt(left) != s.charAt(right)){return false;}return isPalindrome(s, left + 1, right - 1);}

2.動態規劃實現

//動態規劃實現public static String dpLongestPalindromic(String s){if(s == null || s.length() <= 1){return s;}int len = s.length();//存儲下標范圍內的子串是否是回文boolean[][] dp = new boolean[len][len];//記錄最長子串的開始位置和最大長度int start = 0;int maxLen = 1;// 每個單獨的字符都是回文for (int i = 0; i < len; i++) {dp[i][i] = true;}//先對長度為2的字符串進行邏輯判斷，是否滿足回文for (int i = 0; i < len - 1; i++) {if(s.charAt(i) == s.charAt(i+1)){dp[i][i+1] = true;start = i;maxLen = 2;}}//當字符串長度 >= 3時for (int length = 3; length <= len; length++) {for (int i = 0; i <= len-length; i++) {int j = i + length - 1;if(s.charAt(i) == s.charAt(j) && dp[i+1][j-1]){dp[i][j] = true;if(length > maxLen){start = i;maxLen = length;}}}}return s.substring(start, start+maxLen);}

總結：先寫普通遞歸，通過普通遞歸推演動態規劃