????????貪心算法第二篇博客!感覺這篇博客中的算法都很巧妙,需要動動腦筋
122.買賣股票的最佳時機II
????????(這道題可以遍歷數組,如果不能遍歷的話,就不能做了,需要注意的是:
- 只有一只股票!
- 當前只有買股票或者賣股票的操作
????????所以想獲得利潤至少要兩天為一個交易單元。
????????如果想到其實最終利潤是可以分解的,那么本題就很容易了!——如何分解呢?
- 假如第 0 天買入,第 3 天賣出,那么利潤為:prices[3] - prices[0]。
- 相當于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。
- 此時就是把利潤分解為每天為單位的維度,而不是從 0 天到第 3 天整體去考慮!
- 那么根據 prices 可以得到每天的利潤序列:(prices[i] - prices[i - 1]).....(prices[1] - prices[0])。
????????可以發現,其實我們需要收集每天的正利潤就可以,收集正利潤的區間,就是股票買賣的區間,而我們只需要關注最終利潤,不需要記錄區間。那么只收集正利潤就是貪心所貪的地方!
????????局部最優:收集每天的正利潤,全局最優:求得最大利潤。
class Solution:def maxProfit(self, prices: List[int]) -> int:result = 0for i in range(1, len(prices)):# 左閉右開result += max(prices[i] - prices[i - 1], 0)# 取大于0的利潤累加進結果中return result55. 跳躍游戲
????????我想的方法:判斷0的個數及0之前的可走長度,如果能跨過則可以通過(太麻煩了)
????????貪心算法:局部最優解:每次取最大跳躍步數(取最大覆蓋范圍),整體最優解:最后得到整體最大覆蓋范圍,看是否能到終點。
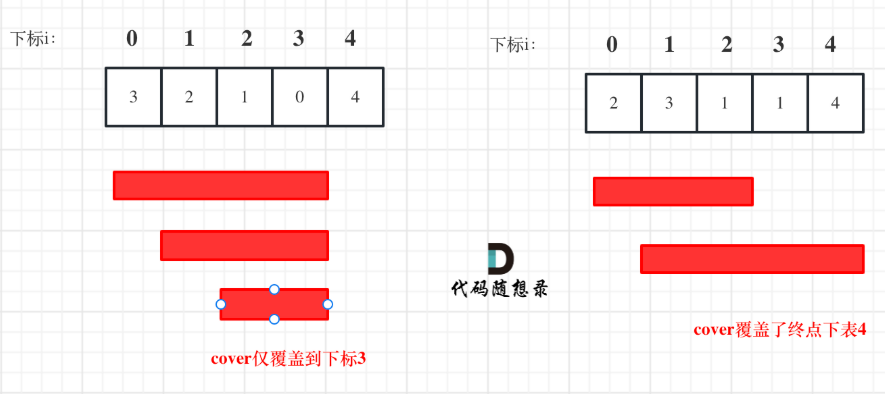
注釋:引用自《代碼隨想錄》
- i 每次移動只能在 cover 的范圍內移動,每移動一個元素,cover 得到該元素數值(新的覆蓋范圍)的補充,讓 i 繼續移動下去。
- 而 cover 每次只取 max(該元素數值補充后的范圍, cover 本身范圍)。
- 如果 cover 大于等于了終點下標,直接 return true 就可以了。
????????不用拘泥于每次究竟跳幾步,而是看覆蓋范圍,覆蓋范圍內一定是可以跳過來的,不用管是怎么跳的。
class Solution:def canJump(self, nums: List[int]) -> bool:cover = 0if len(nums) == 1:return Truei = 0while i <= cover:cover = max(i + nums[i], cover)if cover >= len(nums) - 1:return Truei += 1return False
45.跳躍游戲II?
????????這里需要統計兩個覆蓋范圍,當前這一步的最大覆蓋和下一步最大覆蓋。
? ? ? ? 核心就是這一步的最遠距離沒到終點,才需要加1,繼續下一步的最遠距離……(不斷重復),同時以這一步的最遠距離是否到達終點為判斷條件,來進行加1
? ? ? ? 如何劃分“步”的區間,下一步的區間由上一步區間每個元素統計出的最遠距離而定,區間起點緊鄰上一步
class Solution:def jump(self, nums: List[int]) -> int:if len(nums) == 1:return 0cur_distance = 0 # 當前最遠距離ans = 0 # 記錄步數next_distance = 0 # 下一步覆蓋最遠距離下標for i in range(len(nums)):next_distance = max(nums[i] + i, next_distance)if i == cur_distance:ans += 1 # 需要走下一步cur_distance = next_distance # 規定區間if next_distance >= len(nums) - 1:breakreturn ans1005.K次取反后最大化的數組和
????????第一眼的想法是:排序,統計負數個數
- 如果負數個數l 大于等于k,那么將最小的k個數取反
- 如果負數個數l 小于k,將所有負數取反,同時最小的負數重復取反
bingo!
????????貪心的思路,局部最優:讓絕對值大的負數變為正數,當前數值達到最大,整體最優:整個數組和達到最大。
????????如果將負數都轉變為正數了,K依然大于0,此時的問題是一個有序正整數序列,如何轉變K次正負,讓 數組和 達到最大。
????????那么又是一個貪心:局部最優:只找數值最小的正整數進行反轉,當前數值和可以達到最大(例如正整數數組{5, 3, 1},反轉1 得到-1 比 反轉5得到的-5 大多了),全局最優:整個 數組和 達到最大。
class Solution:def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:nums.sort(key = lambda x: abs(x), reverse = True)# key是排序函數 如 sorted()、list.sort()的參數, 用于指定每個元素在排序前的轉換規則# lambda x: abs(x) 是一個匿名函數, 它接受參數 x 并返回其絕對值 abs(x)# 作用:排序時將根據元素的絕對值大小進行比較,而非元素本身。# 指定排序結果為降序。若省略該參數,默認升序。# lambda 函數: add = lambda a, b: a + bfor i in range(len(nums)):if nums[i] < 0 and k > 0:nums[i] *= -1k -= 1if k % 2 == 1:nums[-1] *= -1result = sum(nums)return result





-狀態欄)

)




實現方式詳解)

:線程封裝)


)
