前言

本篇博客主要介紹卷積基本概念，卷積神經網絡的參數量計算、參數量優化的一些方法（VGG思想，1×1卷積核的應用）、輸出圖像尺寸的計算，同時也介紹了轉置卷積（反卷積）中該如何計算輸出圖像的尺寸大小。

1.卷積

在深度學習的世界里，卷積操作如同一位默默耕耘的幕后英雄，支撐起圖像識別、自然語言處理等眾多領域的技術突破。無論是識別交通標志的自動駕駛系統，還是能理解人類語言的智能助手，背后都離不開卷積操作的強大力量。那么，卷積操作究竟是什么？
從數學角度來看，卷積是一種數學運算，用于描述兩個函數如何通過某種方式相互作用，產生一個新的函數。在離散的數字信號處理場景下，卷積可以簡單理解為兩個序列通過特定的乘法和累加運算，得到一個新的序列，具體計算方式可以總結為8個字：翻褶、移位、相乘、相加，具體可見我之前博客的介紹卷積演示系統
而在計算機視覺領域，卷積與之類似，不同的是，處理的數據維度略有不同。
以3×3卷積核為例，其計算公式可以表示為;
$$g(x,y)=\sum _{i=?1}^1\sum _{j=?1}^{1}f(x?i)(x?j)?w(i,j)$$
其中w(i,j)表示卷積核，f(x,y)輸入圖像，g(x,y)為輸出圖像。
由于在訓練過程中，學習的參數是w(i,j)，因此加不加入翻褶區別并不大，因此在視覺領域一般不對卷積和進行翻褶操作。計算公式為：
$$g(x,y)=\sum _{i=?1}^1\sum _{j=?1}^{1}f(x+i)(x+j)?w(i,j)$$
這一操作準確來說應該稱之為相關操作，但視覺領域一般并不區分這兩種操作，統一稱之為卷積操作。

2.參數量的計算

在計算機視覺領域，卷積核不僅具有寬和高，還具有深度，常寫成寬度×高度×深度的形式。
卷積核的參數不僅包括核中存儲的權值，還包括一個偏置值。

2.1案例一

下面通過一個簡單的例子介紹如何計算卷積和的參數量，這里定義如下網絡：

import torch.nn as nn
class Net1(nn.Module):def __init__(self):super(Net1, self).__init__()self.conv1 = nn.Conv2d(1, 32, 5, padding=1)def forward(self, x):x = self.conv1(x)return x

該網絡包括一個卷積層，輸入通道數為1，輸出通道數為32，卷積核大小為5×5，計算該層的參數量。
解釋：因為輸入通道數為1，因此卷積核大小可以表示為5×5×1，輸出通道數為32，表明該層使用32個卷積核，同時每個卷積核有一個偏置值，因此參數量為：5×5×1×32+32=832。
通過代碼驗證可得：

from ptflops import get_model_complexity_infomodel = Net1()
ops, params = get_model_complexity_info(model, (1, 512, 512), as_strings=True,print_per_layer_stat=False, verbose=True)
params,5*5*1*32+32

運行結果：

這時可以看到，卷積操作的參數量核輸入圖像的尺寸大小無關，上述輸入圖像尺寸為1×512×512，如果使用全連接網絡的話，那么此時輸入層的結點個數為512×512=262144，如果隱含層結點個數為8，那么此時全連接網絡的參數量為262144×8+8，之所以加8，是因為隱含層每個神經元都有一個偏置。
這是可以看到，卷積神經網絡相對于全連接網絡的優勢，權值共享，參數量小。
為什么稱權值共享呢？因為每個特征圖的計算依賴于同一個卷積核。

2.2案例二

為了避免你還未理清如何計算參數量這里再舉一個例子，網絡結構如下：

class Net2(nn.Module):def __init__(self):super(Net2, self).__init__()self.conv1 = nn.Conv2d(8, 32, 3, padding=1)def forward(self, x):x = self.conv1(x)return x

該網絡包括一個卷積層，輸入通道數為8，輸出通道數為32，卷積核大小為3×3，計算該層的參數量。
解釋：因為輸入通道數為8，因此卷積核大小可以表示為3×3×8，輸出通道數為32，表明該層使用32個卷積核，同時每個卷積核有一個偏置值，因此參數量為：3×3×8×32+32=2336。
代碼驗證：

model = Net2()
ops2, params2 = get_model_complexity_info(model, (8, 256, 256), as_strings=True,print_per_layer_stat=False, verbose=True)
params2,3*3*8*32+32

運行結果：

3.奇怪的優化思想

在卷積這一塊，有很多優化思想，來所謂的減少參數量，這里主要介紹兩種主流思想。

3.1使用小核卷積替換大核卷積

該思想來源于VGG網絡的設計思想，論文地址：VGG網絡模型，眾所周知，之所以使用大核卷積，是為了獲得更大的感受野，捕獲更大的局部依賴關系。
前提知識：使用兩個3×3的卷積核的感受野和一個5×5的卷積核的感受野大小一致。
這里我們定義兩個網絡，一個使用小核卷積，另一個使用大核卷積，假設每個卷積操作前后圖像的深度保持不變。
大核卷積網絡結構：

import torch.nn as nn
class Net1(nn.Module):def __init__(self):super(Net1, self).__init__()self.conv1 = nn.Conv2d(32, 32, 5, padding=2)def forward(self, x):x = self.conv1(x)return x

參數量：

小核卷積網絡結構：

class Net3(nn.Module):def __init__(self):super(Net3, self).__init__()self.conv1 = nn.Conv2d(32, 32, 3, padding=1)self.conv2 = nn.Conv2d(32, 32, 3, padding=1)self.relu = nn.ReLU()def forward(self, x):x = self.conv1(x)x = self.relu(x)x = self.conv2(x)x = self.relu(x)return x

參數量：

從結果來看，小核卷積參數量更小，但能夠和大核卷積達到相同的感受野。這就是為什么越來越多的網絡結構使用小核卷積替換大核卷積。

3.2卷積核1×1的應用

這里直接舉兩個例子來介紹：
未使用1×1的卷積核：

class Net4(nn.Module):def __init__(self):super(Net4, self).__init__()self.conv1 = nn.Conv2d(256, 512, 3, padding=1)def forward(self, x):x = self.conv1(x)return x

參數量：

使用1×1卷積核：

class Net5(nn.Module):def __init__(self):super(Net5, self).__init__()self.conv1 = nn.Conv2d(256, 32, 1)self.conv2 = nn.Conv2d(32, 512, 3, padding=1)def forward(self, x):x = self.conv1(x)x = self.conv2(x)return x

參數量：

從結果來看，使用1×1的卷積核減少通道數，能夠在一定程度上減少參數量，但在減少參數量的同時，輸入的信息量也隨之減少，如果輸入的信息是一個稀疏矩陣的話，那么該方法確實適合減少參數量。

4.輸出圖像尺寸的計算

前面所說，都是考慮的是卷積的參數量，接著討論輸出圖像尺寸如何計算。
卷積主要分為三種，Full convolution、Same convolution、valid convolution，這里主要介紹用處較多的一種，即Same convolution

4.1Same convolution

主要是設置padding參數的值
網絡結構：

class Net6(nn.Module):def __init__(self):super(Net6, self).__init__()self.conv2 = nn.Conv2d(32, 512, 3, padding='same')def forward(self, x):x = self.conv2(x)return x

運行測試：

import torch
model = Net6()
I=torch.randn(32,128,128)
model(I).shape

運行結果：

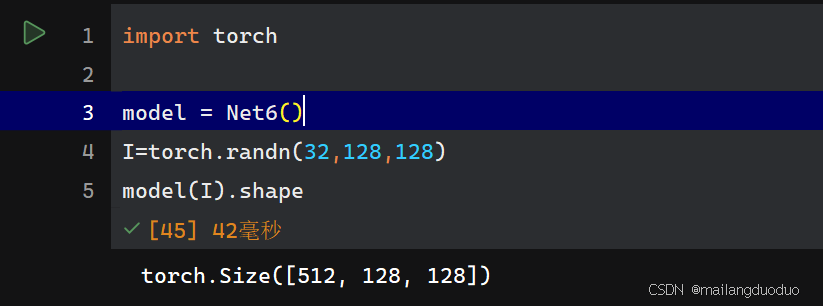
解釋：輸入圖像的尺寸為32×128×128，通過網絡結構可以看出，該層使用512個卷積核，因此輸出通道數為512，因為padding參數設置的是same，輸出會保持圖像的尺寸大小。
有時并不將其設置為same，而是設置一個具體的值，這里只是因為設置了same，其自動計算了一個具體的值代入進去了而已。

4.2具體計算規則

輸出圖像的尺寸，不僅和填充列數有關，還和卷積核大小以及卷積步長有關。具體計算公式如下：
$$W_2=\frac{(W_1?F+2P)}{S}+1$$
$$H_2=\frac{(H_1?F+2P)}{S}+1$$
其中，$W_1、H_1$表示輸入圖像的尺寸大小，$W_2、H_2$表示輸出圖像的尺寸大小，F為卷積核尺寸，S為卷積步長，P為零填充數量。
下面舉一個詳細的例子說明。
網絡結構為：

class Net7(nn.Module):def __init__(self):super(Net7, self).__init__()self.conv2 = nn.Conv2d(32, 512, 5, padding=1,stride=2)def forward(self, x):x = self.conv2(x)return x

輸出結果：

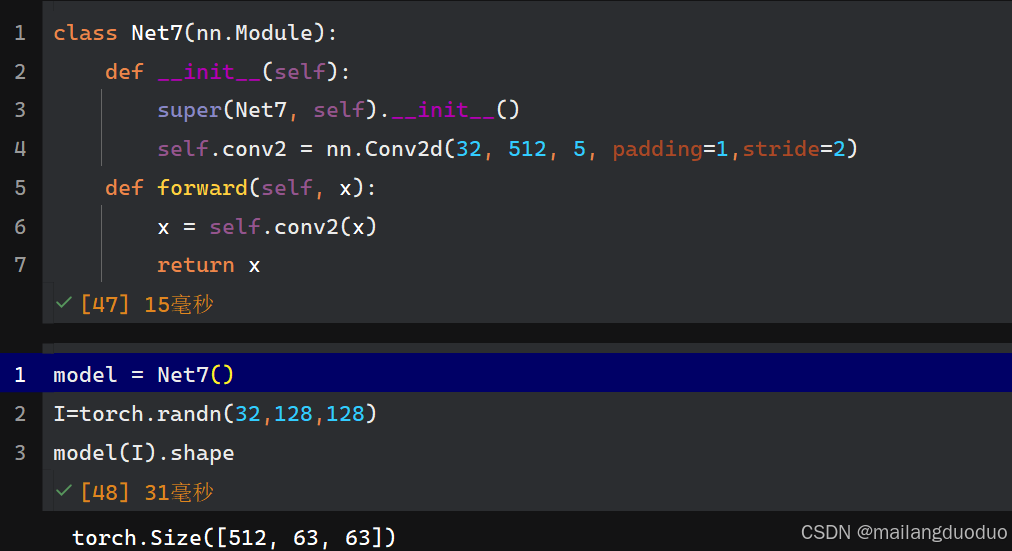
解釋：根據公式計算即可，(128-5+2*1)/2+1=63，除法運算一律向下取整。輸出通道數和卷積核個數512保持一致，因此輸出形狀為512×63×63。

4.3轉置卷積

轉置卷積（Transposed Convolution），又稱反卷積（Deconvolution），具體計算方式也是卷積的逆運算。
由卷積計算公式為：
$$W_2=\frac{(W_1?F+2P)}{S}+1$$
$$H_2=\frac{(H_1?F+2P)}{S}+1$$
轉置卷積，與其計算方式相反，相當于反函數的關系。
$$W_1=S\times (W_2?1)?2P+F$$
$$H_1=S\times (H_2?1)?2P+F$$
其中，$W_1、H_1$表示輸出圖像的尺寸大小，$W_2、H_2$表示輸入圖像的尺寸大小，F為卷積核尺寸，S為卷積步長，P為零填充數量。
下面舉一個詳細的例子說明。

class Net8(nn.Module):def __init__(self):super(Net8, self).__init__()# 轉置卷積self.conv_transpose = nn.ConvTranspose2d(in_channels=32, out_channels=16, kernel_size=3, stride=2, padding=1)def forward(self, x):x = self.conv_transpose(x)return x

輸出結果：

解釋：根據公式計算即可，2*(128-1)-2*1+3，輸出通道數和卷積核個數16保持一致，因此輸出形狀為16×255×255。

小結

通過本篇博客，相比你也能夠計算卷積神經網絡中圖像尺寸如何變化的，快去找一個深層的網絡試試看吧，看它的尺寸變化是否和你想的一樣呢？可以試試本篇博客設計的網絡模型——Unet語義分割模型