【論文閱讀筆記】ICLR 2025 | 解析Ref-Gaussian如何實現高質量可交互反射渲染

Reflective Gaussian Splatting

Info

會議【ICLR 2025】

作者復旦大學，薩里大學；復旦·張力教授團隊

Github地址 https://github.com/fudan-zvg/ref-gaussian.git

Project地址 https://fudan-zvg.github.io/ref-gaussian/

Abstract

新視圖合成得益于越來越強大的NeRF和3DGS方法，經歷了顯著的進展。然而，反射物體的重構仍然具有挑戰性，缺乏在實現實時高質量渲染的同時處理相互反射的適當解決方案。為填補這一空白，我們提出了一種反射高斯重構（Ref-Gaussian）框架，其特點在于兩個組成部分：（I）基于物理的延遲渲染，通過公式化分裂和近似，使渲染方程能夠利用像素級的材料屬性；（II）基于高斯的相互反射，首次在高斯重構范式中實現所需的相互反射函數。為了增強幾何建模，我們進一步引入了材料感知的法線傳播和初始的每個高斯陰影階段，以及二維高斯原語。在標準數據集上進行的大量實驗表明，Ref-Gaussian在定量指標、視覺質量和計算效率方面均優于現有方法。此外，我們展示了我們的方法作為反射和非反射場景的統一解決方案，超越了之前僅關注反射場景的替代方案。同時，我們還說明了Ref-Gaussian支持更多應用，如重光照和編輯。

Introduction

圖1：我們的Ref-Gaussian在新視圖合成中實現了優越的渲染質量，同時享有快速的最優化（訓練時間）和實時渲染（幀率），并支持多種下游應用，如重光照和編輯。

近年來，在多視圖圖像中進行3D物體重構和新視角合成方面取得了巨大的進展。神經輻射場（NeRF）（Mildenhall等，2021）通過神經隱式場表示3D場景，利用體積渲染技術實現高質量、逼真的圖像合成。然而，NeRF在最優化和渲染方面計算開銷較大，限制了其在實時應用中的使用。為了解決這個問題，Kerbl等人（2023）提出的3D高斯點云（3DGS）通過一組3D高斯來表示場景。它結合了光柵化和α混合，實現了實時和高質量渲染。

然而，大多數NeRF和3DGS在建模反射表面方面面臨困難，因為它們固有地無法捕捉高頻鏡面成分。為了解決這個問題，Ref-NeRF（Verbin等，2022）利用集成方向編碼來平滑反射輻射的插值。但是，這種方法未能分解環境照明，使其在重光照方面的應用受到限制。幾種NeRF方法（Verbin等，2022；Liang等，2023）面臨計算成本和靈活性有限的挑戰。在每個高斯上使用簡化的陰影函數可以實現快速收斂，但在幾何、材料和照明建模中卻遭受了大量噪聲（GSShader）。為避免此問題，在像素級別執行陰影函數（即延遲陰影），并通過阿爾法混合來平滑梯度是有幫助的（3DGS-DR）。然而，限制使用簡化的陰影函數使其在建模具有復雜結構和表面的復雜反射物體及其相互反射現象時效果不佳。為了解決后者，RelightableGaussian（Gao等，2023）通過高斯追蹤射線以推斷可見性，但代價是產生大量噪聲和增加了來自蒙特卡羅采樣的計算開銷。

為了綜合解決上述問題，我們提出了一種反射高斯噴濺（RefGaussian）框架，該框架能夠實時高質量地渲染反射物體，同時考慮復雜的相互反射效應。這得益于兩個關鍵組件：（I）基于物理的延遲渲染，我們通過像素級的材料屬性（例如雙向反射分布函數，簡稱BRDF）增強了渲染方程，并采用分裂和近似來避免使用蒙特卡羅采樣時的高計算量；（II）基于高斯的相互反射，我們首次利用高斯噴濺實現了復雜的相互反射函數，盡管提取網格的準確性面臨挑戰。為了增強幾何建模，我們選擇了二維高斯原件作為場景表示，同時引入了初始的每個高斯陰影階段（在高斯級別進行陰影處理以提供良好的幾何初始化），以及一種關注材料的法線傳播過程（擴大具有高金屬度和低粗糙度的高斯的尺度）。

我們做出了以下貢獻：(I) 我們努力實現具有相互反射的反射物體的實時高質量渲染，適用于三維空間。(II) 我們創新了一種通用的三維重構框架——反射高斯濺射（Ref-Gaussian），其特點是基于物理的延遲渲染和高斯基礎的相互反射。該方法通過幾何聚焦的最優化進一步增強，包括采用二維高斯基元、考慮材料的法線傳播和逐高斯的陰影初始化。(III) 大量實驗表明，Ref-Gaussian在反射和非反射場景中，在定量指標、視覺質量和計算效率方面優于之前的方法，同時支持下游應用，如重光照和編輯。

Related Work

在本文中，受到3DGS-DR的啟發，我們采用了像素級的延遲陰影技術，但使用BRDF特性來執行渲染函數，以處理復雜場景。此外，我們建議對提取的網格進行光線追蹤，以計算我們渲染方程中高光成分的可見性。結合渲染方程的分裂和近似，我們在保持快速渲染速度的同時，建模了相互反射效應。

Method

關于 3DGS 和 2DGS 的預備知識就不在這里重復了。

圖2：Ref-Gaussian框架概述：首先，我們應用點濺射過程生成特征圖，并對提取的網格進行光線追蹤，以計算渲染方程中鏡面項的可見性。接下來，我們使用像素級特征圖應用帶分割和求和近似的渲染方程，從而獲得最終的基于物理的渲染結果。

基于物理的延遲渲染

我們基于物理的延遲渲染采用了簡化版的迪士尼BRDF模型（Burley和Studios，2012）。具體而言，每個高斯都與一組與材料相關的屬性相關聯，包括反射率 $λ ∈ [0, 1]^3$ 、金屬度 $m \in [0, 1]$ 和粗糙度 $r \in [0, 1]$ 。法向量 $n ∈ [0, 1]^3$ 可以通過每個二維高斯的切向量推導得出，計算公式為 $n = t_u × t_v$ 。我們在通過alpha混合獲得的像素級特征圖上部署渲染方程：

$\boldsymbol{X}=\sum_{i=1}^{N} \boldsymbol{x}_{i} \alpha_{i} \prod_{j=1}^{i-1}\left(1-\alpha_{j}\right), \quad \text { where } \quad \boldsymbol{X}=\left[\begin{array}{c} \boldsymbol{\Lambda} \\ M \\ R \\ \boldsymbol{N} \end{array}\right], \quad \boldsymbol{x}_{i}=\left[\begin{array}{c} \lambda_{i} \\ m_{i} \\ r_{i} \\ \boldsymbol{n}_{i} \end{array}\right]$

請注意，與在進行 alpha 混合之前直接對高斯進行陰影處理（GSshader）不同，我們的延遲著色將 alpha blending 視為一種平滑濾波器。這使得特征的最優化得以穩定，并最終產生更具一致性的渲染結果。

通過聚合材料圖，包括反射率 $Λ$ 、金屬度 $M$ 、粗糙度 $R$ 和法線 $N$ ，隨后應用渲染方程。渲染方程表示在方向 $ω_o$ 上發出的輻射亮度 $L(ω_o)$ 為：

$L\left(\omega_{o}\right)=\int_{\Omega} L_{i}\left(\omega_{i}\right) f\left(\omega_{i}, \omega_{o}\right)\left(\omega_{i} \cdot \boldsymbol{N}\right) d \omega_{i}$

其中 $f (ω_i, ω_o)$ 表示雙向反射分布函數（BRDF）。它表示在半球上反射入射光的積分。由于 BRDF 包含漫反射和鏡面反射兩個部分，因此積分也可以分為兩個部分。漫反射項通過查詢預積分環境圖并使用法向量 N 進行計算，再與材質項相乘，而鏡面反射項則需要更復雜的反射計算來考慮表面反射。在這里，我們關注鏡面成分，BRDF 的鏡面項為：

$f_{s}\left(\omega_{i}, \omega_{o}\right)=\frac{D G F}{4\left(\omega_{o} \cdot \boldsymbol{N}\right)\left(\omega_{i} \cdot \boldsymbol{N}\right)},$

其中 D、F 和 G 分別表示 GGX 正態分布函數、菲涅爾項和陰影遮蔽項。

為了計算上述積分項，典型的方法是如(Gao et al., 2023)所示的蒙特卡羅采樣。然而，這在實時渲染中計算成本很高。相反，我們采用分裂和近似方法(Munkberg et al., 2022)：

$L_{s}\left(\omega_{o}\right) \approx \int_{\Omega} f_{s}\left(\omega_{i}, \omega_{o}\right)\left(\omega_{i} \cdot \boldsymbol{N}\right) d \omega_{i} \cdot \int_{\Omega} L_{i}\left(\omega_{i}\right) D\left(\omega_{i}, \omega_{o}\right)\left(\omega_{i} \cdot \boldsymbol{N}\right) d \omega_{i} \tag 8$

第一個項僅依賴于 (ωi · N) 和粗糙度 R，這使得結果可以預先計算并存儲在 2D 查找紋理圖中。第二個項表示入射輻射在鏡面光斑上的積分，可以在每次訓練迭代開始時以不同的粗糙度水平進行預積分。這使得可以有效地使用一系列立方圖來表示環境光照，通過使用反射方向和粗糙度作為參數進行三線性插值。

GAUSSIAN GROUNDED 互反射

互反射在渲染反射物體中起著關鍵作用。為此，我們通過分別建模直接光 $L_{dir}$ （方程 8 中的第二項）和間接光 $L_{ind}$ 來進一步增強鏡面光成分。直接光 $L_{dir}$ 是指沒有被任何場景元素阻擋的反射光，其余部分定義為間接光 $L_{ind}$ 。

具體來說，我們根據入射光是否在反射方向 $R = 2(w_o · N )N ? w_o$ 上自遮擋來近似可見度V ∈ {0, 1}。我們將來自遮擋部分的間接光表示為 $L_{ind}$ ：

$L_{s}^{\prime}\left(\omega_{o}\right) \approx\left(\int_{\Omega} f_{s}\left(\omega_{i}, \omega_{o}\right)\left(\omega_{i} \cdot \boldsymbol{N}\right) d \omega_{i}\right) \cdot\left[L_{\mathrm{dir}} \cdot V+L_{\mathrm{ind}} \cdot(1-V)\right] \tag 9$

直觀上，這里引入的間接光成分 $L_{ind}$ 旨在有效建模環境光照估計中由于遮擋引起的擾動。沿著高斯基元的光線計算可見性并非易事。在此，我們提出在提取的網格上動態進行光線追蹤。在優化過程中，我們定期使用截斷帶符號距離函數（TSDF）融合提取物體的表面網格。一旦構建了網格，我們就使用光線追蹤計算光線與表面之間的交點，從而確定每個像素是否被遮擋。為了提高效率，我們采用邊界體積層次（BVH）來加速可見性檢查的光線追蹤過程。至于直接光照Ldir，它僅對應于公式8中的第二項，按照前一部分的描述進行處理。

對于間接光照成分，每個高斯被分配一個額外的視圖依賴顏色 $l_{ind}$ ，該顏色由球面諧波建模。在渲染過程中， $l_{ind}$ 在高斯級別的反射方向上進行評估，并應用 alpha 混合以匯總間接光照圖，如下所示:

$L_{\mathrm{ind}}=\sum_{i=1}^{N} l_{\mathrm{ind}} \alpha_{i} \prod_{j=1}^{i-1}\left(1-\alpha_{j}\right)$

GEOMETRY FOCUSED MODEL OPTIMIZATION

為了促進我們的物理基礎渲染，我們在最優化過程中通過以下設計進一步增強潛在幾何體。

初始階段采用每個高斯著色。由于平滑梯度帶來的代價，像素級陰影在初始階段面臨收斂挑戰，因為陰影函數干擾了幾何體的梯度方向。為了解決這個問題，我們提出了一個專門的初始階段，在該階段渲染方程直接應用于每個高斯基元，利用與之相關的材料和幾何屬性來計算出射輻射。然后，在光柵化過程中對出射輻射進行α混合，以生成最終的PBR渲染。這種高斯級陰影設計可以更有效地將梯度傳遞回高斯基元，并最終促進最優化過程。

材料感知的法線傳播 在法線不準確的位置，往往難以捕捉到顯著的鏡面成分，因為其對反射方向的內在敏感性。我們觀察到，在Ref-Gaussian中，法線準確性與高金屬、低粗糙度特性之間存在強正相關（這是一個鏡面成分顯著的典型情況）。在這一見解的基礎上，我們建議定期增加具有高金屬度和低粗糙度的二維高斯的尺度，以便其法線信息能夠傳播到相鄰的高斯，從而捕捉更精確的幾何形狀。

我們設計了一個以幾何為重點的目標函數： $L = L_c + λ_nL_n + λ_{smooth}L_{smooth}$ ，其中 $Lc = (1 ? λ)L_1 + λL_{D-SSIM}$ 是RGB重構損失，我們設置平衡權重λ = 0.2（Kerbl等，2023）。

第二項 $L_{n}=1-\tilde{\boldsymbol{N}}^{\mathrm{T}} \boldsymbol{N}$ 是Normal一致性損失。它通過最小化渲染法線 N（通過 alpha 混合獲得）與來自深度圖的表面法線 $\tilde N$ 之間的余弦差異，鼓勵高斯與表面對齊。第三項 $L_{smooth} = ∥?N ∥ exp(?∥?Cgt∥) $是一種邊緣感知的法線平滑損失。它旨在正則化低紋理區域的法線變化。

Experiments

為了評估Ref-Gaussian在新視角合成、幾何體、材料和光照重構及下游應用中的性能，我們進行了系列定量和定性實驗。此外，我們在補充材料中提供了一段演示視頻，展示了Ref-Gaussian在兩個合成數據集上的動態渲染，并進行了比較分析。我們選擇了兩個合成數據集，分別是Shiny Blender（Verbin等，2022）和Glossy Synthetic（Liu等，2023），用于反射物體的新視角合成，同時選擇Ref-Real數據集（Verbin等，2022）用于真實世界的開放場景。我們比較了反射3D重構領域中的幾個代表性模型，包括Ref-NeRF（Verbin等，2022）、ENVIDR（Liang等，2023）、3DGS（Kerbl等，2023）、GaussianShader（Jiang等，2024）、可重光照高斯（RelightableGaussian，R3DG）（Gao等，2023）和3DGSDR（Ye等，2024）。我們還與更多基于NeRF的模型進行了比較，如NeRO（Liu等，2023）、NeuS（Wang等，2021）和NDE（Wu等，2024），詳見附錄中的表5和表6。評估指標方面，我們使用了三個標準指標：PSNR、SSIM（Wang等，2004）和LPIPS（Zhang等，2018）。

實現細節 我們的訓練程序分為兩個階段。我們在初始階段使用高斯渲染進行了18,000步的訓練，隨后進入延遲渲染階段，訓練約40,000步。在第二階段之前，我們重置所有顏色和材質屬性，僅保留高斯的幾何形狀。可訓練材質屬性（金屬度、粗糙度和反照率）的學習率均設置為0.005，而環境貼圖的學習率設置為0.01。其他基本可訓練屬性，如位置和協方差，與2DGS（Huang等人，2024）一致。然后，我們對金屬度不低于0.02且粗糙度不高于0.1的高斯進行材質感知法線傳播。此外，我們采用來自3DGS-DR（Ye等人，2024）的金屬初始值，并將初始粗糙度值設置為0.1。在物理基礎渲染的實現過程中，我們發現球諧函數的擬合能力優于集成漫反射光，因此我們使用球諧函數進行替代。對于損失函數， $λ_n$ 設置為0.05， $λ_{smooth}$ 設置為1.0。此外，我們定期以3000步的間隔提取對象的表面網格。所有實驗均在單個NVIDIA A6000圖形處理器上進行。

Comparisons

表 1 每個場景的圖像質量比較在合成的測試視圖上。紅色的強度表示更好的結果。

新視角合成 在表1中，我們展示了多個競爭者以及Ref-Gaussian在多個數據集上的新視圖合成任務的定量結果。Ref-Gaussian在大多數場景中達到了最先進的性能，尤其是在光滑合成數據集上有顯著的改善，這些數據集以反射表面為主。

如圖3所示，3DGS（Kerbl等，2023）在處理高頻的視角依賴效應時遇到困難，導致在多視角場景中（如Bell）反射表面出現明顯的模糊。GShader（Jiang等，2024）引入了顯著的噪聲，導致失真。3DGS-DR（Ye等，2024）采用簡化的陰影函數，但在準確建模復雜的反射場景方面面臨挑戰，如在Luyu和頭盔上的粗糙有色面罩所觀察到的。相比之下，Ref-Gaussian有效地克服了這些挑戰，提供了精準的環境光建模和對復雜幾何體和材料的穩健處理。

此外，在圖4中，我們展示了現實場景的定性比較（Verbin等，2022）。Ref-Gaussian提供了更準確的法線圖和光照，捕捉到了反射表面上的微妙細節。具體而言，花園球體上的反射現象和轎車窗戶上的反射尤為明顯。我們在圖4中展示了Ref-Gaussian更具物理準確性的反射細節捕捉能力。

材料、法線和光照估計 在表2中，我們對競爭者在法線貼圖、環境貼圖和效率方面進行了定量比較。Ref-Gaussian 展示了優越的幾何重構如高質量的法線圖所示。這一改進主要歸因于第3.3節討論的精心設計的幾何優化策略。

如圖5所示，我們的法線圖平滑，其他分解的材質圖也是如此。此外，我們的可見性圖清晰，準確突出反射方向上被遮擋的區域。Ref-Gaussian在估計環境光照方面也在競爭者中取得了最佳結果，這一評估是在縮放后進行的，以消除分歧。

圖6展示了估計環境圖的定性比較。與之前的方法相比，我們的結果在細節和整體色調上與真實值更為接近，同時噪聲量最少。這一改進可歸因于Ref-Gaussian中采用的精確幾何和全面建模。

消融實驗

我們提供了Ref-Gaussian的定量消融研究。

基于物理的渲染 將BRDF屬性分配給高斯函數極大增強了它們表示復雜場景的能力。與3DGS-DR（Ye等，2024）中僅使用一個反射方向向量來查詢環境地圖的簡化陰影函數相比，Ref-Gaussian在學習具有材料變化的場景時表現出顯著更好的性能，例如球體上的粗糙帶（圖7）和頭盔上的面罩（圖3）。

此外，基于物理的渲染有助于幾何重構，這一點在表3的結果中得到了驗證。

基于高斯的相互反射 如圖9所示，我們的相互反射組件對Tbell和Bell的頭部部分影響尤為明顯。通過光線追蹤可見性，我們成功地重構了新視圖合成的間接光照。需要注意的是，相互反射在光澤合成數據集中是少數，其效果在表4中無法完全觀察到。

延遲渲染 我們在每個高斯層級進行基于物理的渲染，并觀察到反射細節的建模明顯變得模糊。如表4所示，未進行延遲渲染時，渲染輸出的所有質量指標顯著下降。

2D高斯原語 如附錄中的圖8、表3和表7所示，強調了2D高斯原語在更精確的幾何表示方面相對于3D替代品的優越性。這是因為3D高斯在體積輻射表示上與表面的薄特性相沖突。值得注意的是，將2D高斯替換為3D高斯，并保持其他組件不變時，Ref-Gaussian在Shiny Blender（Verbin et al., 2022）和Glossy Synthetic（Liu et al., 2023）數據集上的表現依然出色，如附錄中的表7所示。

逐高斯的著色初始化 在初始階段使用基于物理的渲染提供了在幾何收斂的速度和準確率方面顯著的優勢。當我們用相同數量的步驟替換初始階段為基于物理的延遲渲染時，最終結果在各項指標上顯示了渲染質量和法線重構質量的下降。材料感知法線傳播加速了光滑表面的收斂。

表3和表4中呈現的定量比較展示了其在幾何重構中的有效性。如圖10所示，光滑表面容易發生幾何崩潰，但我們的材料感知法線傳播有效解決了這個問題。

材料感知法線傳播 材料感知法線傳播加速了光滑表面的收斂。表3和表4中提供的定量比較展示了其在幾何重構中的有效性。如圖10所示，光滑表面容易發生幾何崩潰，但我們的材料感知法線傳播有效地解決了這個問題。

總結

在本文中，我們介紹了一種新穎的高斯濺射框架——Ref-Gaussian，該框架旨在實時高質量地重構反射物體/場景。這是通過構建兩個集成組件實現的：基于物理的延遲渲染和高斯基礎的相互反射，以及聚焦幾何的模型優化。我們還展示了選擇基礎表示模型的重要性，其中2DGS優于3D替代方案。在多個數據集上的廣泛實驗表明，Ref-Gaussian在定量指標、視覺質量和效率方面優于現有方法。此外，我們還展示了Ref-Gaussian在重新照明和編輯等其他應用中的效果。

Appendix

Limitations

由于Ref-Gaussian是專門為重建反射場景而設計的，因此在處理非鏡面場景時可能表現不佳。在建模相互反射時，我們僅考慮反射方向上的可見性，以近似整個鏡面葉片的總體可見性。雖然這種方法顯著降低了渲染的計算復雜性，但由于近似的固有不準確性，它可能會在材料估計中引入一些噪聲。

重新照明和編輯的定性結果

在非鏡面數據集上的進一步定量比較

根據設計，Ref-Gaussian 在反射和非反射場景中均表現出色，使其成為建模各種具有不同反射特性的場景的統一解決方案。這是因為，如公式9所述,內部反射僅作為一個附加元素納入鏡面成分中。因此，在反射較弱的場景中，內部反射的影響自然減弱，并隨著金屬屬性的降低而相應減小。在這種情況下，漫反射成分取而代之，包含任何（通常相對微弱的）內部反射效應的捕捉，以實現最佳性能。

這種行為在附錄中的圖5和圖14所提供的分解結果中顯而易見。相比之下，以前專注于反射的替代方案，如 3DGS-DR（Ye et al., 2024），專門設計用于反射場景，這導致了應用范圍的縮小。

為了支持這一說法，我們在附錄中包含了表8，展示了在主要由非反射場景組成的 NeRF-Synthetic 數據集（Mildenhall et al., 2020）上，Ref-Gaussian、3DGS-DR（Ye et al., 2024）和 3DGS（Kerbl et al., 2023）之間的逐場定量比較，以進行新視圖合成。結果表明，我們的 Ref-Gaussian 仍然優于這兩種替代方案，驗證了其通用和統一的優勢。

基于Nerf方法的額外基線

間接成分對REF-REAL數據集的定性結果

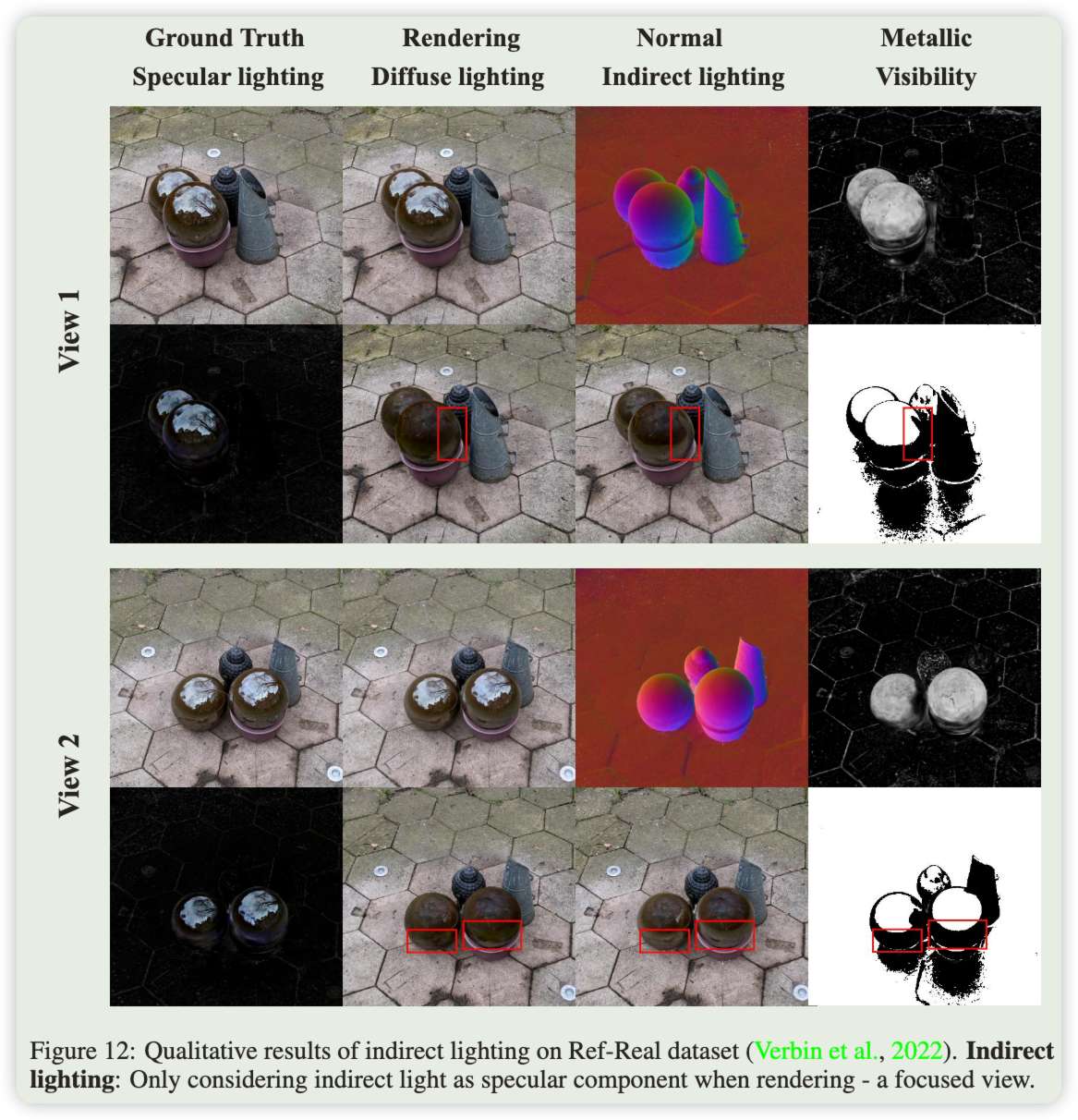
我們在圖12中提供了更豐富的定性結果，其中多個物體提供了豐富的相互反射。可以觀察到，在新視圖合成的任務中，三個組件——漫反射、鏡面反射和間接光——有效地互為補充，共同產生了出色的最終渲染結果。具體而言，基于金屬屬性，漫反射組件主要對石球外部的非反射物體和地面細節進行建模。鏡面反射組件則關注石球上那些反射光未被地面或其他物體遮擋的部分，捕捉細致的反射細節，而間接光組件有效捕捉地面和鄰近物體的投影。這些分解結果強烈表明，Ref-Gaussian即使在復雜的現實場景中，也能通過其精心設計的渲染方法和精確的幾何重構，準確捕捉各種細節。

綜合2DGS消融研究的定量結果

為了明確展示2DGS表示的效果，并更公平、全面地證明Ref-Gaussian相對于其他技術的優越性，我們將Ref-Gaussian的2DGS表示替換為3DGS，同時保持其他部分不變以進行比較，如表7所示。2DGS的引入顯著增強了模型的性能。值得強調的是，基于3DGS構建的Ref-Gaussian在Shiny Blender（Verbin等，2022）和Glossy Synthetic（Liu等，2023）數據集的大多數場景中也表現出色，進一步突顯了該渲染模型的內在優越性。