地球重力場有兩種表達方法：

1、拉普拉斯（Laplace）方法，將重力場展開為球諧級數。

2、斯托克斯（Stokes）方法，根據地球的總質量和旋轉角速度計算。

本篇主要說第一種方法，該方法將地球表面觀測的重力值f(θ,φ)展開成球諧函數Y的級數：

?

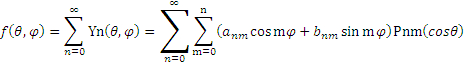
其中，θ為余緯，φ經度，Y為拉普拉斯方程的解，為球諧函數。

Pnm是締合（連帶）勒讓德多項式，勒讓德多項式的m階導數。

水平實在有限，只能理解到這種程度。

球諧函數Y只與θ，φ有關，與球諧函數Y的大小r無關，如果用球面的顏色表示球諧函數的值，則l=5,m=2時，圖像如下：

r的計算公式如下：

因此，球諧函數及其它們的和的圖形表示如下：

上圖中n即是l，k即是m。負階導數的概念如下：

對于函數f(x)，如果它的一階導數存在，那么f(x)的倒數1/f(x)的導數就是負一階導數。

GRACE重力衛星通過GPS和K波段測距儀以1cm的精度精確測量兩顆子衛星的間距，從而獲得地球重力場的信息，經過濾波處理后可以得到地球靜態的重力場模型。再通過球諧函數的線性疊加即可得到大地水準面的形態，其大地水準面表達式如下：

由于大地水準面接近旋轉橢球面，而旋轉橢球面又是大地測量的基準面，如果采用實際地球的長半徑、扁率，引力場參數及旋轉角速度作為橢球參數，就能得到一個與大地水準面幾何形狀和外部重力場都很符合的水準橢球。大地水準面扣除參考橢球面（一般為WGS84橢球體）就可以推算出大地水準面的起伏和重力異常。

ICGEM網站上有很多地球靜態重力場模型，見下圖。

圖中Degree就是階，gfz文件就是球諧函數的系數文件。根據系數文件就可以計算地球任一點的重力場值，網絡上有相關計算過程。如果不會（博主也不會），ICGEM提供了在線計算過程。

下圖是選擇第一行的WHU-SWPU-GOGR2022的300階系數文件。

計算重力異常格網如下圖。

參考文獻

https://blog.csdn.net/xiaokcehui/article/details/145836165?spm=1001.2014.3001.5501

https://qingping-liu.github.io/%E7%90%83%E8%B0%90%E5%87%BD%E6%95%B0%E5%8F%AF%E8%A7%86%E5%8C%96.html

https://blog.csdn.net/absll/article/details/124941810

https://icgem.gfz-potsdam.de/calcgrid

基于球諧函數的重力異常和垂線偏差誤差匹配關系_萬曉云2017

https://blog.csdn.net/u010087338/article/details/118438788

https://zhuanlan.zhihu.com/p/430163791