【算法學習】遞歸、搜索與回溯算法（二）

算法學習：

https://blog.csdn.net/2301_80220607/category_12922080.html?spm=1001.2014.3001.5482

前言：

在（一）中我們挑了幾個經典例題，已經對遞歸、搜索與回溯算法進行了初步講解，今天我們來進一步講解這幾個算法知識點，主要是進行了一些拔高，比如引入了剪枝的操作，來看今天的例題吧

目錄

1. 經典例題

1.1 全排列 ||

1.2 組合總和

1.3 N皇后

1.4 有效的數獨

1.5 單詞搜索

1.6 不同路徑 |||

2. 總結

1. 經典例題

1.1 全排列 ||

47. 全排列 II

給定一個可包含重復數字的序列?nums?，按任意順序?返回所有不重復的全排列。

示例 1：

輸入：nums = [1,1,2]
輸出：
[[1,1,2],[1,2,1],[2,1,1]]

示例 2：

輸入：nums = [1,2,3]
輸出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

  • 1 <= nums.length <= 8
  • -10 <= nums[i] <= 10

算法原理：

這道題與(一)中的全排列|解法上區別不大，唯一不同的是這里需要有剪枝操作，因為全排列一中序列中的數字都不相同，這里序列中的數字是可以相同的

我們看上面這個示例，觀察這個策略樹發現有些分支上面畫著x，這些就是錯誤分支，需要我們剪掉，其中橙紅色的x代表的是同一個數被再次使用的錯誤分支，綠色的x代表的是同一層節點中相同元素被多次使用的錯誤分支
基于上面的剪掉錯誤分支的原理，我們的代碼可以從兩個角度切入，一個是:只關心不合法的分支;一個是:只關心合法的分支

代碼實現：

class Solution {vector<vector<int>> ret;vector<int> path;bool check[10];
public:vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(),nums.end());dfs(nums);return ret;}void dfs(vector<int>& nums){if(path.size()==nums.size()){ret.push_back(path);return;}for(int i=0;i<nums.size();i++){//只關注不合法的分支，當是不合法的分支時，需要剪掉，所以不進入遞歸if(check[i]==true||(i!=0&&nums[i]==nums[i-1]&&check[i-1]==false))continue;//只關注合法的分支的做法就是將上面if中的條件相反，然后把下面的內容包在函數體內path.push_back(nums[i]);check[i]=true;dfs(nums);path.pop_back();check[i]=false;}}
};

1.2 組合總和

LCR 081. 組合總和

給定一個無重復元素的正整數數組?candidates?和一個正整數?target?，找出?candidates?中所有可以使數字和為目標數?target?的唯一組合。

candidates?中的數字可以無限制重復被選取。如果至少一個所選數字數量不同，則兩種組合是不同的。?

對于給定的輸入，保證和為?target?的唯一組合數少于?150?個。

示例 1：

輸入: candidates = [2,3,6,7], target = 7<
輸出: [[7],[2,2,3]]

示例 2：

輸入: candidates = [2,3,5], target = 8
輸出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

輸入: candidates = [2], target = 1
輸出: []

示例 4：

輸入: candidates = [1], target = 1
輸出: [[1]]

示例 5：

輸入: candidates = [1], target = 2
輸出: [[1,1]]

提示：

  • 1 <= candidates.length <= 30
  • 1 <= candidates[i] <= 200
  • candidate?中的每個元素都是獨一無二的。
  • 1 <= target <= 500

算法原理：

代碼實現：

class Solution {vector<vector<int>> ret;vector<int> path;int sum;
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {dfs(candidates,target,0);return ret;}void dfs(vector<int>& candidates,int target,int pos){if(sum>=target){if(sum==target) ret.push_back(path);return;}for(int i=pos;i<candidates.size();i++){sum+=candidates[i];path.push_back(candidates[i]);dfs(candidates,target,i);path.pop_back();sum-=candidates[i];}}
};

1.3 N皇后

51. N 皇后

按照國際象棋的規則，皇后可以攻擊與之處在同一行或同一列或同一斜線上的棋子。

n?皇后問題?研究的是如何將?n?個皇后放置在?n×n?的棋盤上，并且使皇后彼此之間不能相互攻擊。

給你一個整數?n?，返回所有不同的?n?皇后問題?的解決方案。

每一種解法包含一個不同的?n 皇后問題?的棋子放置方案，該方案中?'Q'?和?'.'?分別代表了皇后和空位。

示例 1：

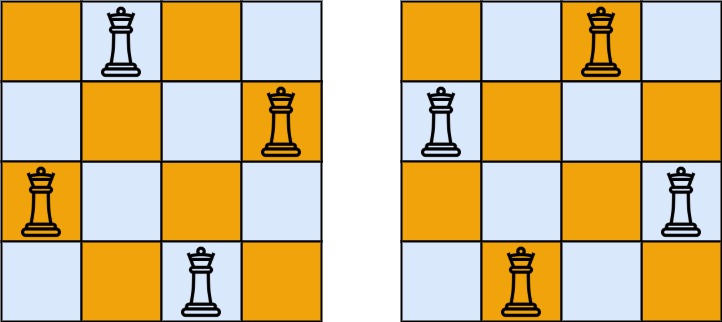
輸入：n = 4
輸出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解釋：如上圖所示，4 皇后問題存在兩個不同的解法。

示例 2：

輸入：n = 1
輸出：[["Q"]]

提示：

  • 1 <= n <= 9

算法原理：

解釋:

這道題最關鍵的就是我們上面的剪枝操作，根據題意我們知道在一個nxn棋盤中，一個列中只能存在一個元素，所以我們可以創建一個bool數組col來標記列的元素情況我們把棋盤抽象到坐標系上，因為對角線上也只能有一個元素，對角線可以有如圖的兩種，這兩種它們x+y都是一個定值，所以也可以創建bool數組來對它們進行標記

y-x可能為負數，負數不能作為bool數組的下標，所以可以加上一個n的偏移量

代碼實現：

class Solution {bool checkCol[10],checkDigal1[20],checkDigal2[20];vector<vector<string>> ret;vector<string> path;int n;
public:vector<vector<string>> solveNQueens(int _n) {n=_n;path.resize(n);for(int i=0;i<n;i++)path[i].append(n,'.');dfs(0);return ret;}void dfs(int row){if(row==n){ret.push_back(path);return;}for(int col=0;col<n;col++)    //嘗試在這一行放置皇后{//剪枝if(!checkCol[col]&&!checkDigal1[row-col+n]&&!checkDigal2[row+col]){path[row][col]='Q';checkCol[col]=checkDigal1[row-col+n]=checkDigal2[row+col]=true;dfs(row+1);//恢復現場path[row][col]='.';checkCol[col]=checkDigal1[row-col+n]=checkDigal2[row+col]=false;}}}
};

1.4 有效的數獨

36. 有效的數獨

請你判斷一個?9 x 9?的數獨是否有效。只需要?根據以下規則?，驗證已經填入的數字是否有效即可。

  1. 數字?1-9?在每一行只能出現一次。
  2. 數字?1-9?在每一列只能出現一次。
  3. 數字?1-9?在每一個以粗實線分隔的?3x3?宮內只能出現一次。（請參考示例圖）

注意：

  • 一個有效的數獨（部分已被填充）不一定是可解的。
  • 只需要根據以上規則，驗證已經填入的數字是否有效即可。
  • 空白格用?'.'?表示。

示例 1：

輸入：board = 
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
輸出：true

示例 2：

輸入：board = 
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
輸出：false
解釋：除了第一行的第一個數字從 5 改為 8 以外，空格內其他數字均與 示例1 相同。 但由于位于左上角的 3x3 宮內有兩個 8 存在, 因此這個數獨是無效的

提示：

  • board.length == 9
  • board[i].length == 9
  • board[i][j]?是一位數字（1-9）或者?'.'

算法原理：

解釋:

這題不是回溯類的題，但是通過這題我們可以更好的理解N皇后那道題，這道題也是要保證數據在一定位置上不能重復出現，所以都可以采取哈希的方式(這里的數組模擬的就是哈希)進行標記，這道題要求同一行、同一列和同一個九宮格中都不能出現相同的方式所以我們就可以用三個bool數組來進行標記，我們拿第一個row[9][10]來舉例，這表示的就是第i行0~9每個數字的存在情況，需要注意的是第三個數組，它用來標記每個九宮格里數字的出現情況，所以我們把整個大表格分為3x3九份，同時后面的【10】是用來記錄各個數字出現情況，而且grid數組對應的下標其實就是【x/3】【y/3】

代碼實現：

class Solution {bool col[9][10];bool row[9][10];bool grid[3][3][10];
public:bool isValidSudoku(vector<vector<char>>& board) {for(int i=0;i<9;i++){for(int j=0;j<9;j++){if(board[i][j]>='0'&&board[i][j]<='9'){int num=board[i][j]-'0';if(row[i][num] ||col[j][num]||grid[i/3][j/3][num]) return false;row[i][num]=col[j][num]=grid[i/3][j/3][num]=true;}}}return true;}
};

1.5 單詞搜索

79. 單詞搜索

給定一個?m x n?二維字符網格?board?和一個字符串單詞?word?。如果?word?存在于網格中，返回?true?；否則，返回?false?。

單詞必須按照字母順序，通過相鄰的單元格內的字母構成，其中“相鄰”單元格是那些水平相鄰或垂直相鄰的單元格。同一個單元格內的字母不允許被重復使用。

示例 1：

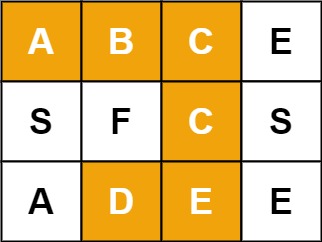
輸入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
輸出：true

示例 2：

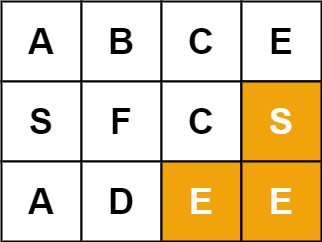
輸入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
輸出：true

示例 3：

輸入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
輸出：false

提示：

  • m == board.length
  • n = board[i].length
  • 1 <= m, n <= 6
  • 1 <= word.length <= 15
  • board?和?word?僅由大小寫英文字母組成

算法原理：

代碼實現：

class Solution {bool vis[7][7];int m,n;
public:bool exist(vector<vector<char>>& board, string word) {m=board.size(),n=board[0].size();for(int i=0;i<m;i++)for(int j=0;j<n;j++){if(board[i][j]==word[0]){vis[i][j]=true;if(dfs(board,i,j,word,1)) return true;vis[i][j]=false;}}return false;}int dx[4]={0,0,1,-1},dy[4]={1,-1,0,0};bool dfs(vector<vector<char>>& board,int i,int j,string& word,int pos){if(pos==word.size()) return true;for(int k=0;k<4;k++){int x=i+dx[k], y=j+dy[k];if(x>=0 && x<m &&y>=0 &&y<n &&board[x][y]==word[pos] &&vis[x][y]==false){vis[x][y]=true;if(dfs(board,x,y,word,pos+1)) return true;vis[x][y]=false;}}return false;}
};

1.6 不同路徑 |||

980. 不同路徑 III

在二維網格?grid?上，有 4 種類型的方格：

  • 1?表示起始方格。且只有一個起始方格。
  • 2?表示結束方格，且只有一個結束方格。
  • 0?表示我們可以走過的空方格。
  • -1?表示我們無法跨越的障礙。

返回在四個方向（上、下、左、右）上行走時，從起始方格到結束方格的不同路徑的數目。

每一個無障礙方格都要通過一次，但是一條路徑中不能重復通過同一個方格。

示例 1：

輸入：[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
輸出：2
解釋：我們有以下兩條路徑：
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)

示例 2：

輸入：[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
輸出：4
解釋：我們有以下四條路徑： 
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)

示例 3：

輸入：[[0,1],[2,0]]
輸出：0
解釋：
沒有一條路能完全穿過每一個空的方格一次。
請注意，起始和結束方格可以位于網格中的任意位置。

提示：

  • 1 <= grid.length * grid[0].length <= 20

這道題可以用動歸來解決，但是難度比較大，用爆搜簡單一點

這道題原理之類與前面幾題很相似，我們把思路搞明白就很容易上手，根據題意，我們要做的是從1出發，遍歷所有的0，然后到達2
我們可以把所有能夠到達2的路徑都嘗試一遍，其中許多路徑肯定是沒有把0全部遍歷的，這種的就需要被剪掉，我們可以采取一種更簡單的方式，我們可以定義一個常量count用來記錄我們所走過的0的個數，然后當我們走到終點時判斷一下我們所走的0的個數與整個表格中0的個數是否一樣，一樣就代表我們把所有的0都遍歷過了

代碼實現：

class Solution {int dx[4]={1,-1,0,0};int dy[4]={0,0,-1,1};int step=0;int m,n;int ret=0;bool vis[20][20];
public:int uniquePathsIII(vector<vector<int>>& grid) {m=grid.size(),n=grid[0].size();int bx=0,by=0;for(int i=0;i<m;i++)for(int j=0;j<n;j++){if(grid[i][j]==0) step++;else if(grid[i][j]==1) bx=i,by=j;}step+=2;vis[bx][by]=true;dfs(grid,bx,by,1);return ret;}void dfs(vector<vector<int>>& grid,int i,int j,int path){if(grid[i][j]==2){if(step==path)ret++;return;}for(int k=0;k<4;k++){int x=i+dx[k],y=j+dy[k];if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]!=-1&&vis[x][y]==false){vis[x][y]=true;dfs(grid,x,y,path+1);vis[x][y]=false;}}}
};

2. 總結

上一篇主要講解的是遞歸、搜索與回溯算法的一些基本知識和簡單例題，本篇的一些題型結合深搜和寬搜的知識，還要用到一些剪枝的操作，總體來說難度大了很多，需要花費更多的時間在上面

本篇筆記：

感謝各位大佬觀看，創作不易，還望各位大佬點贊支持！！

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/pingmian/79972.shtml
繁體地址，請注明出處：http://hk.pswp.cn/pingmian/79972.shtml
英文地址，請注明出處：http://en.pswp.cn/pingmian/79972.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

HTTP請求與緩存、頁面渲染全流程

HTTP請求與緩存、頁面渲染全流程

文章目錄 前言**1. HTTP請求與緩存處理****緩存機制**? 強緩存&#xff08;Cache-Control / Expires&#xff09;? 協商緩存&#xff08;Last-Modified / ETag&#xff09; **2. 服務器響應與數據解析****3. HTML DOM 構建****4. CSSOM 構建****5. 渲染樹&#xff08;Render …
閱讀更多...
限流算法學習筆記（一）Go Rate Limiter

限流算法學習筆記（一）Go Rate Limiter

文章目錄 1. 背景與概述1.1 什么是速率限制1.2 Go Rate Limiter 的定義與價值 2. 核心思想與設計理念2.1 令牌桶算法的基本原理2.2 惰性評估設計2.3 多種處理策略的平衡2.4 簡單易用的偶發控制 3. 架構設計與組件3.1 整體架構3.2 Limiter 組件3.3 Reservation 組件3.4 Limit 類…
閱讀更多...
n8n工作流自動化平臺的實操：生成統計圖的兩種方式

n8n工作流自動化平臺的實操：生成統計圖的兩種方式

1.成果展示 1.1n8n的工作流 牽涉節點&#xff1a;Postgres、Code、QuickChart、Edit Fields、HTTP Request 12.顯示效果 2.實操過程 2.1節點說明 2.1.1Postgres節點&#xff1a; 注&#xff1a;將明細數據進行匯總。 2.1.2code節點&#xff1a; 注&#xff1a;將 查詢的數…
閱讀更多...
JavaScript中數組和對象不同遍歷方法的順序規則

JavaScript中數組和對象不同遍歷方法的順序規則

在JavaScript中&#xff0c;不同遍歷方法的順序規則和適用場景存在顯著差異。以下是主要方法的遍歷順序總結&#xff1a; 一、數組遍歷方法 for循環 ? 嚴格按數組索引順序遍歷&#xff08;0 → length-1&#xff09; ? 支持break和continue中斷循環 ? 性能最優&#xff0c;…
閱讀更多...
緩存（1）：三級緩存

緩存（1）：三級緩存

三級緩存是指什么 我們常說的三級緩存如下&#xff1a; CPU三級緩存Spring三級緩存應用架構&#xff08;JVM、分布式緩存、db&#xff09;三級緩存 CPU 基本概念 CPU 的訪問速度每 18 個月就會翻 倍&#xff0c;相當于每年增? 60% 左右&#xff0c;內存的速度當然也會不斷…
閱讀更多...
Android setContentView()源碼分析

Android setContentView()源碼分析

文章目錄 Android setContentView()源碼分析前提setContentView() 源碼分析總結 Android setContentView()源碼分析 前提 Activity 的生命周期與 ActivityThread 相關&#xff0c;調用 startActivity() 時&#xff0c;會調用 ActivityThread#performLaunchActivity()&#xf…
閱讀更多...
uniapp自定義步驟條(可二開進行調試)

uniapp自定義步驟條(可二開進行調試)

前言 有一個業務需求是需要一個步驟條&#xff0c;但是發現開源的都不太合適&#xff0c;所以就自己寫了一個。 開始 test.vue <template><view class"authenticateRecordDetails_container"><!-- 進度 --><view class"authenticateSte…
閱讀更多...
22、近端策略優化算法（PPO）論文筆記

22、近端策略優化算法（PPO）論文筆記

近端策略優化算法&#xff08;PPO&#xff09;論文筆記 一、研究背景與目標二、**方法****3.1 策略梯度基礎****3.2 信任區域方法&#xff08;TRPO&#xff09;****3.3 剪切代理目標函數&#xff08;LCLIP&#xff09;****3.4 自適應KL懲罰系數****3.5 算法實現** 三、 L CLIP…
閱讀更多...
web 自動化之 Selenium 元素定位和瀏覽器操作

web 自動化之 Selenium 元素定位和瀏覽器操作

文章目錄 一、元素定位的八大方法1、基于 id/name/class/tag_name 定位2、基于 a 標簽元素的鏈接文本定位3、基于xpath定位4、css定位 二、瀏覽器操作1、信息獲取2、 瀏覽器關閉3、 瀏覽器控制 一、元素定位的八大方法 web 自動化測試就是通過代碼對網頁進行測試&#xff0c;在…
閱讀更多...
前端面經 作用域和作用域鏈

前端面經 作用域和作用域鏈

含義&#xff1a;JS中變量生效的區域 分類&#xff1a;全局作用域 或者 局部作用域 局部作用域&#xff1a;函數作用域 和 塊級作用域ES6 全局作用域:在代碼中任何地方都生效 函數中定義函數中生效&#xff0c;函數結束失效 塊級作用域 使用let或const 聲明 作用域鏈:JS查…
閱讀更多...
【C/C++】RPC與線程間通信：高效設計的關鍵選擇

【C/C++】RPC與線程間通信：高效設計的關鍵選擇

文章目錄 RPC與線程間通信&#xff1a;高效設計的關鍵選擇1 RPC 的核心用途2 線程間通信的常規方法3 RPC 用于線程間通信的潛在意義4 主要缺點與限制4.1 缺點列表4.2 展開 5 替代方案6 結論 RPC與線程間通信&#xff1a;高效設計的關鍵選擇 在C或分布式系統設計中&#xff0c;…
閱讀更多...
兩種方法求解最長公共子序列問題并輸出所有解

兩種方法求解最長公共子序列問題并輸出所有解

最長公共子序列&#xff08;Longest Common Subsequence, LCS&#xff09;是動態規劃領域的經典問題&#xff0c;廣泛應用于生物信息學&#xff08;如DNA序列比對&#xff09;、文本差異比對&#xff08;如Git版本控制&#xff09;等領域。本文將通過??自頂向下遞歸記憶化??…
閱讀更多...
SpringBoot應急知識學習系統開發實現

SpringBoot應急知識學習系統開發實現

概述 一個基于SpringBoot開發的應急知識學習系統&#xff0c;該系統提供了完整的用戶注冊、登錄、知識學習與測評功能。對于開發者而言&#xff0c;這是一個值得參考的免費Java源碼項目&#xff0c;可以幫助您快速構建類似的教育平臺。 主要內容 5.2 注冊模塊的實現 系統采…
閱讀更多...
【Python 字符串】

【Python 字符串】

Python 中的字符串&#xff08;str&#xff09;是用于處理文本數據的基礎類型&#xff0c;具有不可變性、豐富的內置方法和靈活的操作方式。以下是 Python 字符串的核心知識點&#xff1a; 一、基礎特性 定義方式&#xff1a; s1 單引號字符串 s2 "雙引號字符串" s…
閱讀更多...
第十六屆藍橋杯大賽軟件賽C/C++大學B組部分題解

第十六屆藍橋杯大賽軟件賽C/C++大學B組部分題解

第十六屆藍橋杯大賽軟件賽C/C大學B組題解 試題A: 移動距離 問題描述 小明初始在二維平面的原點&#xff0c;他想前往坐標(233,666)。在移動過程中&#xff0c;他只能采用以下兩種移動方式&#xff0c;并且這兩種移動方式可以交替、不限次數地使用&#xff1a; 水平向右移動…
閱讀更多...
如何使用極狐GitLab 軟件包倉庫功能托管 npm？

如何使用極狐GitLab 軟件包倉庫功能托管 npm？

極狐GitLab 是 GitLab 在中國的發行版&#xff0c;關于中文參考文檔和資料有&#xff1a; 極狐GitLab 中文文檔極狐GitLab 中文論壇極狐GitLab 官網 軟件包庫中的 npm 包 (BASIC ALL) npm 是 JavaScript 和 Node.js 的默認包管理器。開發者使用 npm 共享和重用代碼&#xff…
閱讀更多...
Matlab 基于Hough變換的人眼虹膜定位方法

Matlab 基于Hough變換的人眼虹膜定位方法

1、內容簡介 Matlab220-基于Hough變換的人眼虹膜定位方法 可以交流、咨詢、答疑 2、內容說明 略 3、仿真分析 略 4、參考論文 略
閱讀更多...
chili調試筆記14 畫線 頁面布置 線條導出dxf

chili調試筆記14 畫線 頁面布置 線條導出dxf

2025-05-08 09-05-06 llm畫線 頁面布置 expand有自己的格式 刪了就會按照子元素格式 不加px無效 沒有指定尺寸設置100%無效 怎么把線條導出dxf command({name: "file.export",display: "command.export",icon: "icon-export", }) export class…
閱讀更多...
藍綠發布與金絲雀發布

藍綠發布與金絲雀發布

藍綠發布與金絲雀發布 一、藍綠發布&#xff1a;像「搬家」一樣安全上線1. 生活化故事2. 技術步驟拆解步驟①&#xff1a;初始狀態步驟②&#xff1a;部署新版本到綠環境步驟③&#xff1a;內部驗證綠環境步驟④&#xff1a;一鍵切換流量步驟⑤&#xff1a;監控與回滾 3. 藍綠發…
閱讀更多...
【2025五一數學建模競賽B題】 礦山數據處理問題｜建模過程+完整代碼論文全解全析

【2025五一數學建模競賽B題】 礦山數據處理問題｜建模過程+完整代碼論文全解全析

你是否在尋找數學建模比賽的突破點&#xff1f;數學建模進階思路&#xff01; 作為經驗豐富的美賽O獎、國賽國一的數學建模團隊&#xff0c;我們將為你帶來本次數學建模競賽的全面解析。這個解決方案包不僅包括完整的代碼實現&#xff0c;還有詳盡的建模過程和解析&#xff0c…
閱讀更多...
最新文章

Copyright @ 2022~2023