第6章:阻力
目錄
- 引言
- 寄生阻力
- 誘導阻力
- 減少誘導阻力的方法
- 升力對寄生阻力的影響
- 飛機總阻力
- 飛機總重量對總阻力的影響
- 高度對總阻力的影響
- 構型對總阻力的影響
- 速度穩定性
- 所需功率(簡介)
- 總結
- 問題
- 附件A
- 附件B
- 附件C
- 答案
引言
阻力是阻礙飛機前進運動的力。阻力與相對氣流平行且方向相同(與飛行路徑方向相反)。請記住,在考慮氣流速度時,飛機在空氣中移動還是空氣流過飛機并不會對氣流模式產生任何差異:相對速度才是重要因素。
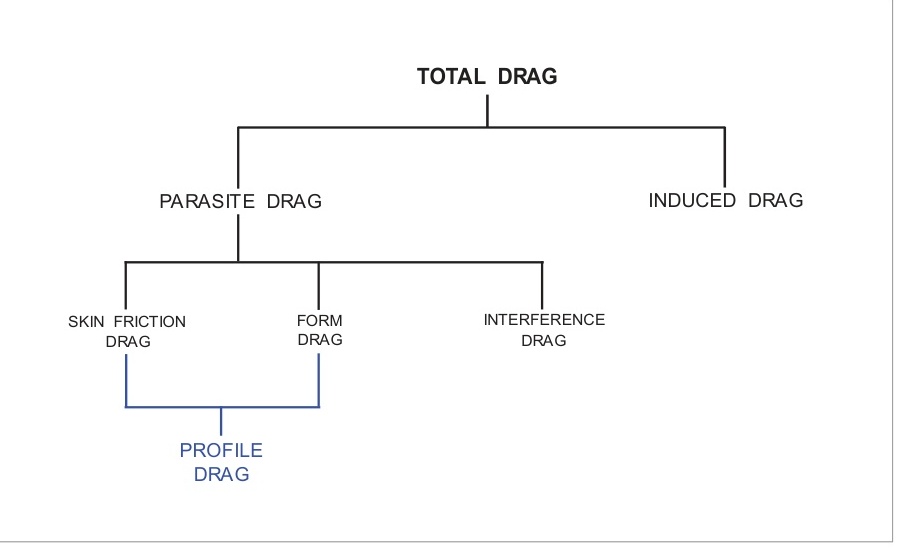
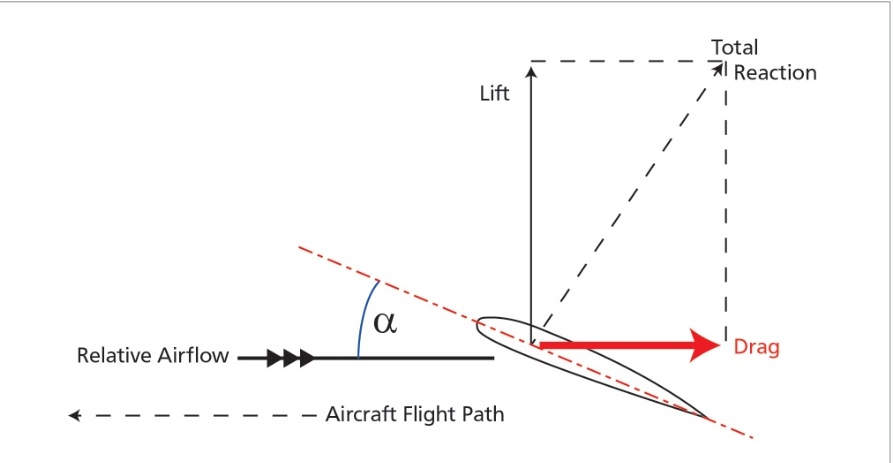
飛機暴露在氣流中的每個部分都會產生不同類型的前進阻力,這些阻力共同構成總阻力。總阻力分為兩種主要類型:
寄生阻力——與升力產生無關,以及
誘導阻力——升力產生的結果。
寄生阻力進一步細分為:
-
表面摩擦阻力
-
形狀(壓力)阻力,以及
-
干擾阻力
注意:表面摩擦阻力和形狀阻力合稱為型阻力。
誘導阻力將在后面討論。我們首先考慮寄生阻力的各個要素。
寄生阻力
如果飛機以零升力攻角飛行,存在的唯一阻力將是寄生阻力。寄生阻力由"表面摩擦"、"形狀"和"干擾"阻力組成。
表面摩擦阻力
與表面直接接觸的空氣粒子被加速到飛機的速度并隨之移動。相鄰的粒子將通過與下層粒子接觸而加速,但由于空氣粘度較低,它們的速度將略低于飛機。隨著與表面距離的增加,空氣層的加速越來越小。因此,在整個表面上將存在一層空氣,其相對速度從表面的零到受飛機存在影響的空氣邊界處的最大值。從表面延伸到無法檢測到粘性效應的點的空氣層被稱為邊界層。在飛行中,邊界層的性質將決定最大升力系數、失速特性、形狀阻力值,以及在某種程度上決定飛機的高速特性。
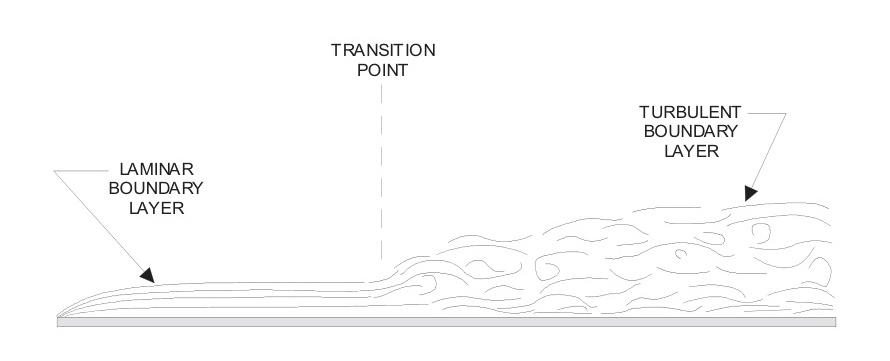
考慮如圖6.3所示的空氣流過平面表面的情況。邊界層將以兩種形式存在,即層流或湍流。通常,前部的流動是層流,在一定距離后變為湍流,這個點稱為轉捩點。湍流中表面速度變化率的增加將產生比層流更大的表面摩擦。湍流邊界層也比層流層具有更高的動能水平。
轉捩點向前移動將增加表面摩擦,因為湍流區域將更大。轉捩點的位置取決于:
-
表面狀況 - 薄層流層對表面不規則性極為敏感。飛機前部任何表面粗糙度都會在該點引起向湍流的轉捩,并且增厚的湍流邊界層將向下游扇形擴散,導致表面摩擦阻力顯著增加。
-
不利壓力梯度(圖6.4)- 當壓力在流動方向上升高時,層流層無法存在。在曲面上,如翼型,轉捩點通常位于或接近最大厚度點。由于曲面上存在不利壓力梯度,轉捩點將比平面表面更靠前。
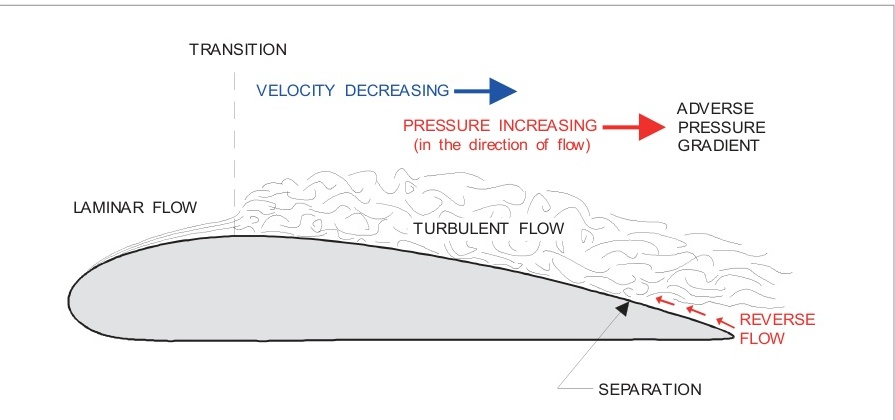
注意:上述草圖中邊界層的垂直比例被大大夸大。通常,邊界層厚度從前緣的2毫米增加到后緣約20毫米。
形狀(壓力)阻力
形狀(壓力)阻力是由物體前緣的壓力大于后緣壓力而產生的。總體而言,表面摩擦導致邊界層動能隨著流動沿表面向后移動而持續減少。轉捩點后的不利壓力梯度將導致邊界層動能進一步減少。如果邊界層在不利壓力梯度存在的情況下沒有足夠的動能,邊界層的下層將停止移動(停滯)。邊界層的上層將在此點(分離點)超越,邊界層將在分離點與表面分離。見圖6.4。此外,分離點后的表面流動將向前,朝向分離點——流動反轉。由于分離,后緣的壓力將低于前緣。空氣動力學力將朝著較低壓力的方向作用——形狀阻力。
當邊界層在給定的不利壓力梯度存在的情況下沒有足夠的動能時,將發生分離。
邊界層動能的損失可能由各種因素引起。
-
隨著攻角增加,轉捩點移向前緣,不利壓力梯度變得更強。這導致分離點向前移動。最終,邊界層分離將發生在非常接近前緣的位置,以至于沒有足夠的機翼面積提供所需的升力, C L C_{L} CL?將減小,發生失速。
-
當激波在上表面形成時,通過激波的靜壓增加將產生極端不利的壓力梯度。如果激波足夠強,分離將立即發生在激波后面。這將在第13章-高速飛行中詳細解釋。
層流和湍流分離
已經表明,分離是由氣流遇到不利壓力梯度引起的,但發現湍流邊界層在遇到相同壓力梯度時比層流邊界層更能抵抗分離。在這方面,湍流邊界層比層流邊界層更可取,但從阻力角度看,層流更可取。
流線型設計
飛機的每個部分都會受到形狀(壓力)阻力的影響。為了減少形狀阻力,有必要將分離點延遲到盡可能接近后緣的位置。流線型設計增加了物體長度與深度之間的比例,減少了表面的曲率,從而減少了不利壓力梯度。細長比是衡量流線型程度的指標。已經發現理想的細長比是3:1,如圖6.5所示。
注意:在暴露于氣流的組件連接處添加整流罩和填角(見第10頁術語表)也被稱為"流線型設計"。
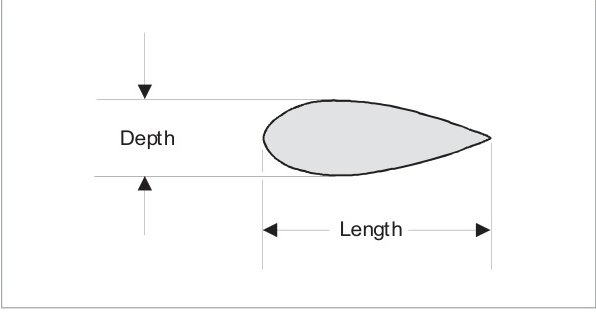
型阻力
表面摩擦阻力和形狀阻力的組合被稱為型阻力。可以認為這些阻力是由飛機呈現給相對氣流的"型面"(或橫截面積)產生的。
干擾阻力
當考慮完整的飛機時,寄生阻力將大于各部分的總和。額外的阻力來自于機翼/機身、機翼/發動機短艙等連接處的邊界層"干擾"。需要填角來最小化干擾阻力。
影響寄生阻力的因素
-
指示空速
-
寄生阻力與指示空速(IAS)的平方成正比。
-
如果IAS加倍,寄生阻力將增加四倍;如果IAS減半,寄生阻力將是原來的四分之一。
-
構型
寄生阻力與呈現給氣流的正面面積成正比;這被稱為"寄生面積"。如果展開襟翼、放下起落架、選擇減速板或操作滾轉控制擾流板,"寄生面積"將增加,寄生阻力也將增加。
-
機身污染
冰、霜、雪、泥或雪泥的污染將增加寄生阻力系數,在嚴重的機身結冰情況下,還會增加寄生面積。
寄生阻力公式
D p = 1 / 2 ρ V 2 C D p S D_{p}=1/2ρV^{2}C_{Dp}S Dp?=1/2ρV2CDp?S
其中,
| 符號 | 描述 |
|---|---|
| D P D_{P} DP? | 寄生阻力 |
| 1/2 V2 | 動壓 (Q) |
| C D p \mathrm{C}_{\mathrm{Dp}} CDp? | 寄生阻力系數 |
| S | 面積(寄生面積) |
誘導阻力
誘導阻力是升力的不良副產品。翼尖渦流修改了機翼附近的上洗和下洗,產生了升力矢量的后向分量,稱為誘導阻力。
IAS越低,攻角越高——渦流越強。
渦流越強——誘導阻力越大。
翼尖渦流
機翼上表面的氣流壓力低于下表面。后緣和翼尖是氣流相互作用的地方,圖6.6。壓力差異改變了流動方向,在上表面誘導出朝向根部的展向矢量,在下表面誘導出朝向尖端的展向矢量。“常規地”,從后方觀察飛機。右翼尖將產生逆時針渦流,左翼尖將產生順時針渦流,圖6.7。在較高的攻角(較低的IAS),減小的弦向矢量將增加合成的展向流動,使渦流更強。
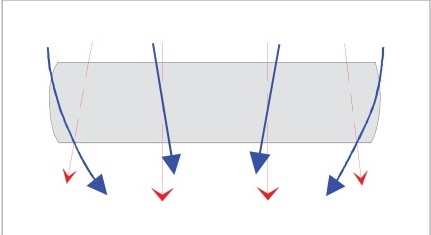
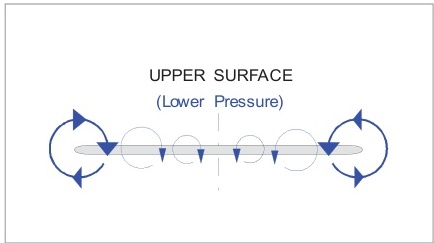
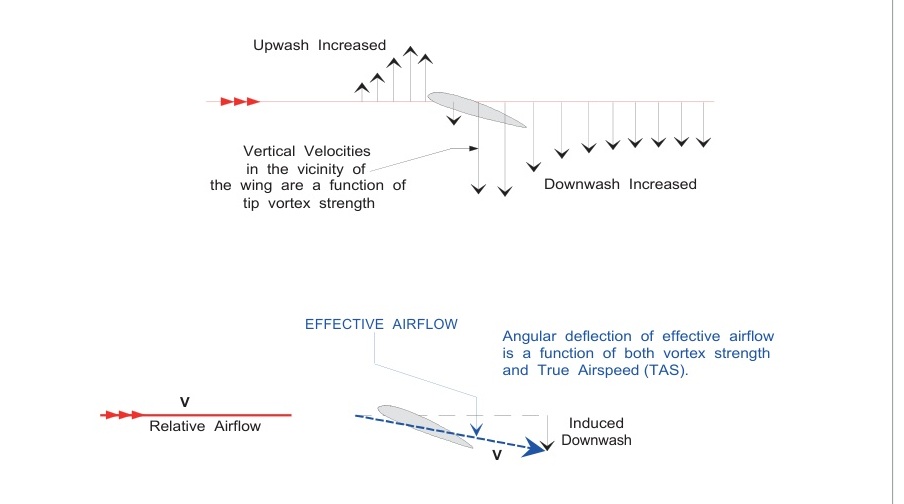
誘導下洗
翼尖渦流在機翼附近的氣流中產生某些垂直速度分量,包括機翼前方和后方,圖6.9。這些垂直速度增強了上洗和下洗,減小了有效攻角。渦流越強,有效攻角的減小越大。
由于有效攻角的局部減小,機翼產生的總升力將低于在沒有展向壓力差的情況下產生的值。升力的產生本身減少了所產生的升力大小。
為了替代因增加的上洗和下洗而損失的升力,機翼必須以比原本必要的更高的攻角飛行。這增加了阻力。這種額外的阻力被稱為誘導阻力,圖6.10。
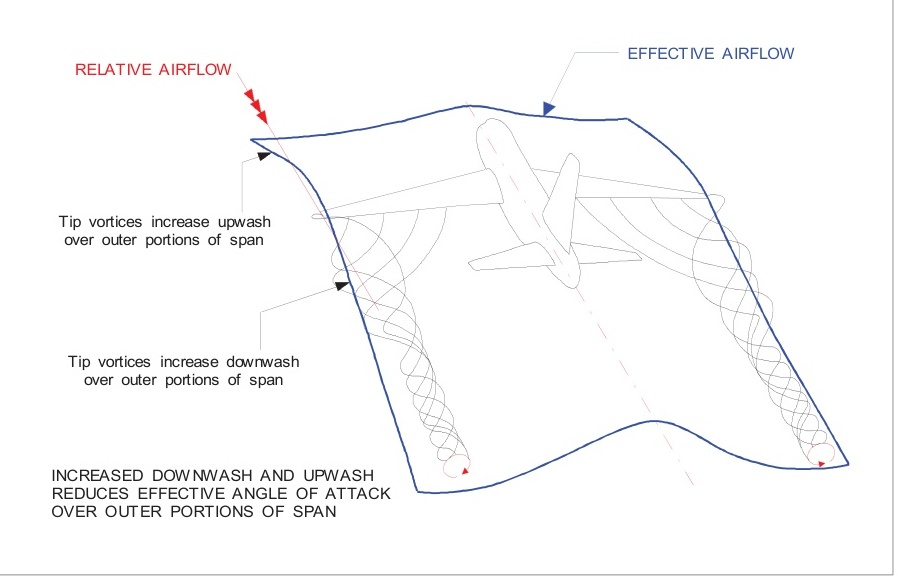
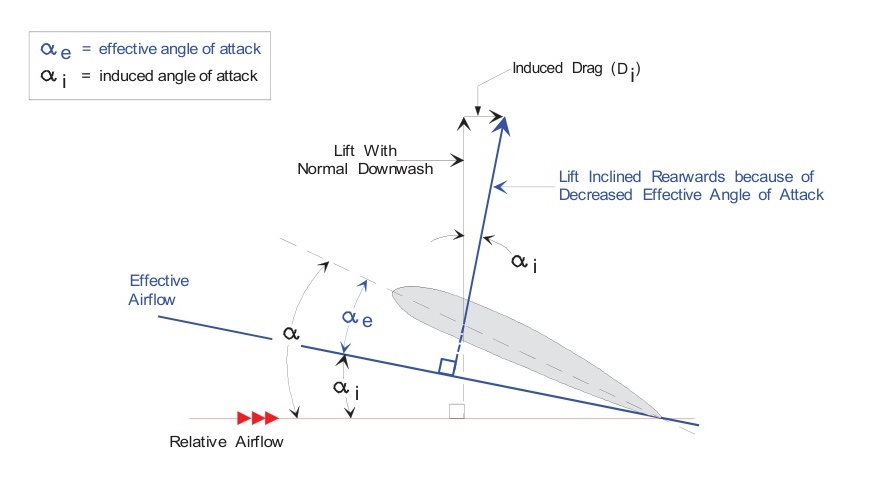
影響誘導阻力的因素:
升力大小 - 因為誘導阻力是升力的一個分量,升力越大,誘導阻力就越大。在平飛時升力必須等于重量,所以誘導阻力將取決于飛機的重量。飛機重量越大,誘導阻力越大。某些機動需要升力大于飛機重量。升力與重量的關系被稱為"載荷系數"(或"g")。例如,在穩定轉彎期間,升力大于重量,所以在穩定轉彎期間的誘導阻力將高于直線平飛時的誘導阻力。因此,隨著載荷系數的增加,誘導阻力也會增加。誘導阻力將與升力的平方成正比增加。
飛機的速度 - 誘導阻力隨著速度的增加而減小(對于恒定的升力)。這是因為,隨著速度增加,由翼尖渦流引起的下洗變得不那么顯著,升力的后向傾斜較小,因此誘導阻力較小。誘導阻力與速度的平方成反比變化。(參見第121頁詳細解釋)。
機翼的展弦比 - 高展弦比機翼的翼尖渦流影響的展向比例較小,因此下洗的整體變化將較小,給升力力量的后向傾斜也較小。因此,隨著展弦比的增加,誘導阻力減小(對于給定的升力)。誘導阻力系數與展弦比成反比。
從前面三個因素可以推導出以下方程:
C D i = C L 2 A R \mathrm {C}_{\mathrm {Di}}=\frac {\mathrm {C}_{\mathrm {L}}^{2}}{\mathrm {AR}} CDi?=ARCL2??
可以看出,誘導阻力系數 ( C D i ) \left(C_{Di}\right) (CDi?)的關系強調了對于設計用于在飛行大部分時間內以較高升力系數運行的飛機構型(即傳統高速噴氣式運輸機)需要高展弦比機翼。
展弦比對升力和阻力特性的影響如圖6.11和圖6.12所示。這些圖上顯示了基本翼型剖面特性,這些特性僅適用于極高(無限)展弦比的機翼平面形狀。當用這種基本剖面構建某個有限展弦比的機翼時,主要差異將在升力和阻力特性上——力矩特性基本保持不變。
增加展弦比對升力曲線的影響,如圖6.11所示,是減小產生給定升力系數所需的機翼攻角。較高展弦比的機翼對攻角變化更敏感,但需要較小的攻角才能達到最大升力。
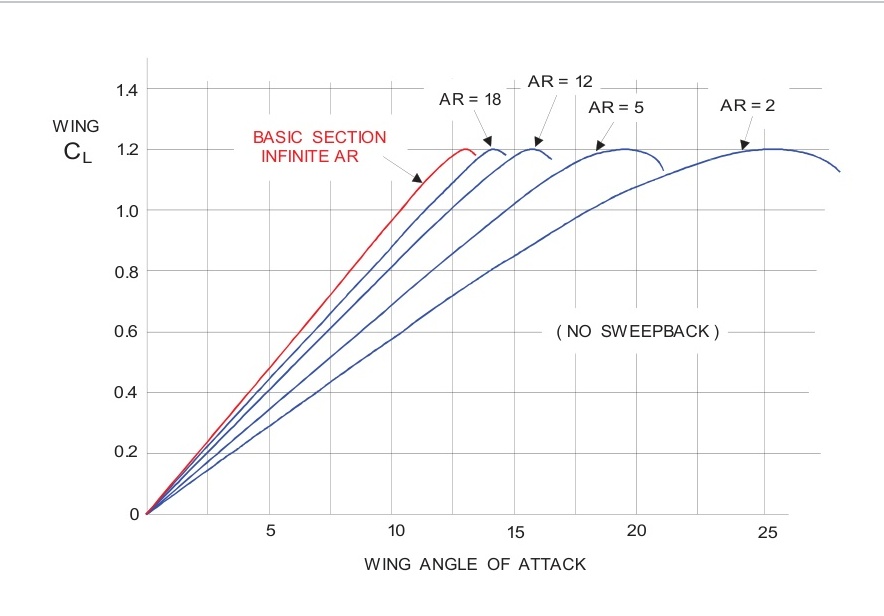
從圖6.12可以看出,在任何升力系數下,較高的展弦比會給出較低的機翼阻力系數,因為誘導阻力系數與展弦比成反比。當展弦比高時,誘導阻力隨升力的變化很小。在高升力系數(低IAS)下,誘導阻力非常高,并且隨著升力系數的增加而迅速增加。
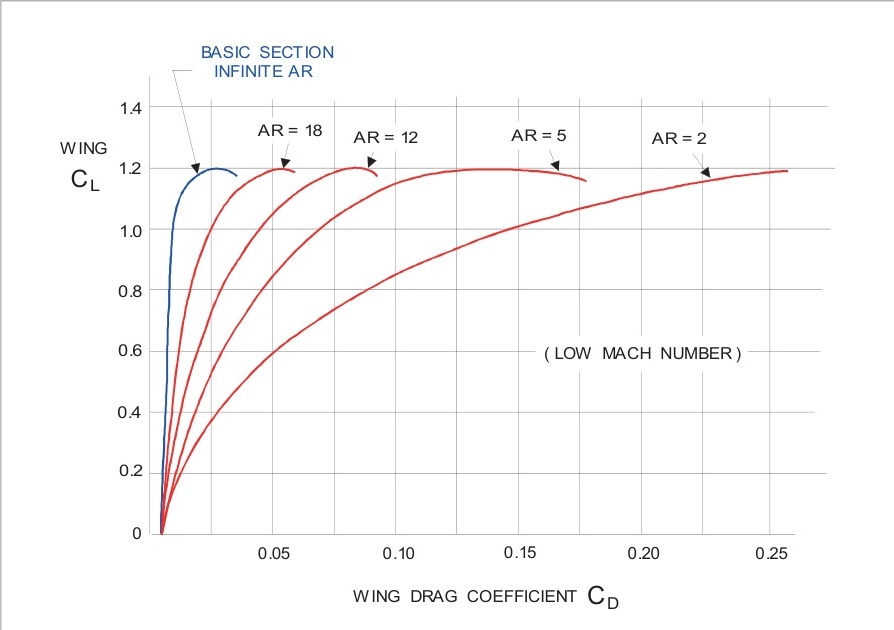
高展弦比機翼的升力和阻力曲線,圖6.11和圖6.12,顯示 C L \mathrm {C}_{\mathrm {L}} CL?隨 a a a持續強烈增加直至失速,而 C D C_{D} CD?僅在失速點有較大變化。
繼續增加展弦比受到以下考慮的限制。
非常高展弦比的機翼將經歷以下情況:
-
過大的機翼彎曲力矩:可以通過在機翼中攜帶燃油并將發動機安裝在機翼下方的吊艙中來減輕。
-
降低滾轉速率(特別是在低空速時):這是由于下降的機翼(僅在實際下降時)經歷增加的有效攻角。增加的有效攻角是由于機翼的前向真空速和尖端的角真空速的合成。展弦比越高,對于給定的滾轉速率,尖端的垂直真空速越大,導致有效攻角增加越多。尖端處的有效攻角越高,對滾轉的阻力越大。這種現象被稱為空氣動力阻尼,將在后面的章節中更詳細地介紹。
-
在起飛和著陸期間滾轉時地面間隙減少。
誘導阻力系數 ( C D i ) (C_{Di}) (CDi?)
D i = 1 / 2 ρ V 2 C D i S D_{i}=1/2ρ\mathbf {V}^{2}\mathrm {C}_{\mathrm {Di}} S Di?=1/2ρV2CDi?S
這個方程似乎暗示誘導阻力 ( D , ) (D,) (D,)隨速度增加而增加,但誘導阻力系數 ( C D i ) \left(C_{Di}\right) (CDi?)與 C L 2 \mathrm {C}_{\mathrm {L}}^{2} CL2?成正比,與機翼展弦比成反比。隨著速度增加,為了保持恒定的升力, C L C_{L} CL?必須減小。因此,隨著速度增加, C D i \mathrm {C}_{\mathrm {Di}} CDi?減小:
C D i = C L 2 A R \mathrm {C}_{\mathrm {Di}}=\frac {\mathrm {C}_{\mathrm {L}}^{2}}{\mathrm {AR}} CDi?=ARCL2??
以下例子說明了 C D i \mathrm {C}_{\mathrm {Di}} CDi?隨速度變化的情況,這導致了 D i D_{i} Di?的變化。
如果飛機的速度從80節 ( 41 m / s ) (41m/s) (41m/s)增加到 160 節 ( 82 m / s ) 160節(82m/s) 160節(82m/s),動壓將增加四倍。(在例子中使用了海平面ISA密度,但任何恒定密度都會給出相同的結果)。
Q = 1 / 2 ρ ~ V 2 \mathrm {Q}=1/2ρ\mathrm {\sim V}^{2} Q=1/2ρ~V2
Q = 0.5 × 1.225 × 41 × 41 = 1029.6 Q=0.5\times 1.225\times 41\times 41=1029.6 Q=0.5×1.225×41×41=1029.6
Q = 0.5 x 1.225 x 82 x 82 = 4118.4 Q=0.5x1.225x82x82=4118.4 Q=0.5x1.225x82x82=4118.4
參考升力公式: L = Q C L S S L = Q C_L SS L=QCL?SS
如果由于速度加倍而動壓增加四倍, C L C_{L} CL?必須減少到原來的四分之一才能保持恒定的升力。
將原來 C L C_{L} CL?的 1 / 4 1/4 1/4應用到 C D i \mathrm {C}_{\mathrm {Di}} CDi?公式:
C D i = C L 2 A R \mathrm {C}_{\mathrm {Di}}=\frac {\mathrm {C}_{\mathrm {L}}^{2}}{\mathrm {AR}} CDi?=ARCL2??
C D i = ( 1 / 4 ) 2 A R \mathrm {C}_{\mathrm {Di}}=\frac {(1/4)^{2}}{\mathrm {AR}} CDi?=AR(1/4)2? 因為AR是常數 C D i = ( 1 / 4 ) 2 = 1 16 C_{Di}=(1/4)^{2}= \frac{1}{16} CDi?=(1/4)2=161?
如果將原來 C D i \mathrm {C}_{\mathrm {Di}} CDi?的 1 / 16 1/16 1/16應用到誘導阻力公式:
D i = ( Q × 4 ) × 1 / 16 = 1 / 4 D_{i}=(Q\times 4)\times 1/16=1/4 Di?=(Q×4)×1/16=1/4
結論:如果在平飛中速度加倍:動壓將增加四倍, C L C_{L} CL?必須減少到原來的 1 / 4 1/4 1/4, C D i \mathrm {C}_{\mathrm {Di}} CDi? w i wi wi是原來的 1 / 16 1/16 1/16,而 D i D_{i} Di?將減少到原來的 1 / 4 1/4 1/4。
如果在平飛中速度減半:動壓將是原來的 1 / 4 1/4 1/4, C L \mathrm {C}_{\mathrm {L}} CL?需要增加到原來的四倍, C D i \mathrm {C}_{\mathrm {Di}} CDi?將是原來的16倍,產生四倍的 D i D_{i} Di?。
減少誘導阻力的方法
誘導阻力在高速時較低,但在低速時它占總阻力的一半以上。誘導阻力取決于尾渦的強度,已經表明高展弦比機翼可以減少給定升力下渦流的強度。然而,非常高的展弦比會增加機翼根部彎曲力矩,降低滾轉速率,并在起飛和著陸期間滾轉時減少地面間隙;因此,展弦比必須保持在實際限制內。以下列表列出了通過減弱翼尖渦流來最小化誘導阻力的其他方法。
-
機翼端板:放置在翼尖的平板將限制翼尖渦流,并具有類似于增加展弦比的效果,但沒有額外的彎曲載荷。然而,板本身會產生寄生阻力,在較高速度下可能不會有總體阻力節省。
-
翼尖油箱:放置在翼尖的燃油箱將具有類似于端板的有益效果,將減少誘導阻力,并且還將減少機翼根部彎曲力矩。
-
翼尖小翼:這些是形成翼尖一部分的小型垂直翼型(圖6.13)。根據誘導氣流的形狀和角度,它們產生一個小的前向力(即"負阻力"或推力)。翼尖小翼部分阻擋了從底部流向機翼上表面的空氣,減少了翼尖渦流的強度。此外,翼尖小翼產生的小渦流與主翼尖渦流相互作用,進一步減少了主翼尖渦流的強度。
-
翼尖形狀:翼尖的形狀可以影響翼尖渦流的強度,向下或向上翻轉的翼尖等設計已被用來減少誘導阻力。
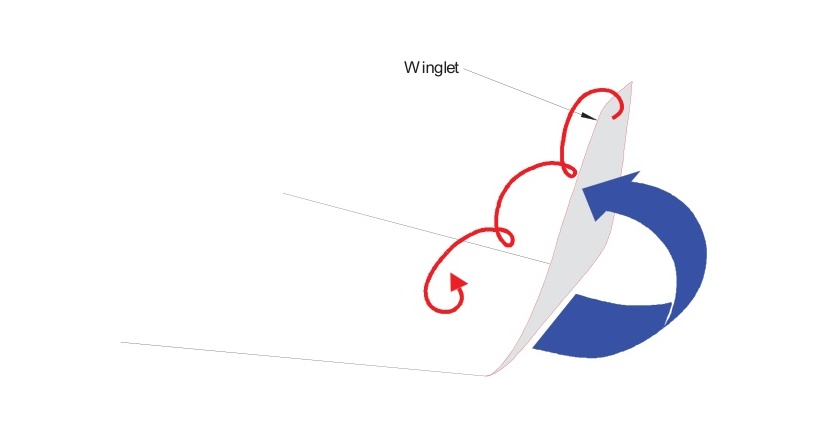
升力對寄生阻力的影響
形狀、摩擦和干擾引起的阻力總和被稱為"寄生"阻力,因為它與升力的產生沒有直接關系。雖然寄生阻力與升力的產生沒有直接關系,但實際上它確實隨升力而變化。圖6.14顯示了典型飛機的寄生阻力系數 C D p \mathrm {C}_{\mathrm {Dp}} CDp?隨升力系數 C L C_{L} CL?的變化。
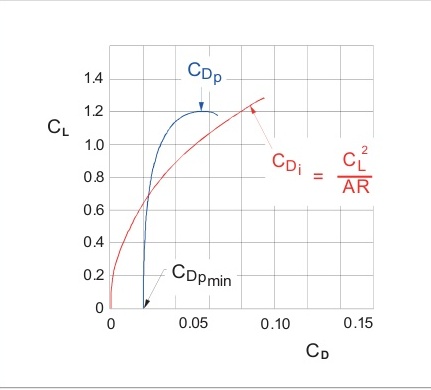
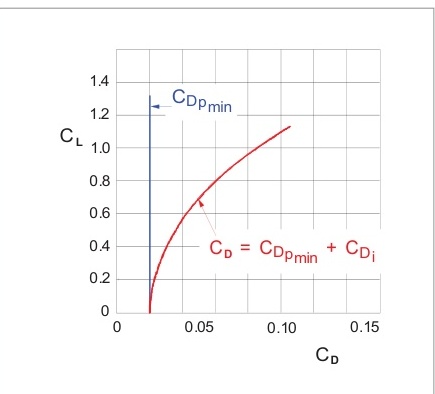
然而,零升力以上的寄生阻力部分被包含在誘導阻力系數中。圖6.15。
構型的影響
寄生阻力 D p D_{p} Dp?不受升力影響,但隨動壓和面積變化。如果所有其他因素保持不變,寄生阻力隨正面面積顯著變化。例如,放下起落架和襟翼可能會使寄生面積增加多達 80 % 80\% 80%。在任何給定的IAS下,這架飛機將經歷 80 % 80\% 80%的寄生阻力增加。
高度的影響
在大多數飛行階段,飛機將以恒定的IAS飛行,動壓和寄生阻力不會變化。在高空提供相同的IAS時,真空速會更高。
速度的影響
單獨速度對寄生阻力的影響是最重要的。如果所有其他因素保持不變,速度加倍將使動壓增加四倍,因此寄生阻力增加四倍(或者在原始速度的一半時寄生阻力為原來的四分之一)。寄生阻力隨速度的這種變化表明,寄生阻力在高IAS時最為重要,而在低動壓時則不那么重要。為了說明這一點,一架在失速速度略高處飛行的飛機可能有的寄生阻力僅占總阻力的 25 % 25\% 25%。然而,這同一架飛機在最大水平飛行速度下的寄生阻力幾乎是總阻力的 100 % 100\% 100%。寄生阻力在高飛行速度下的主導地位強調了獲得高速性能需要極高的空氣動力學清潔度(流線型)。
飛機總阻力
飛行中飛機的總阻力是誘導阻力和寄生阻力的總和。圖6.16說明了特定重量和構型下飛機在平飛時總阻力隨IAS的變化。
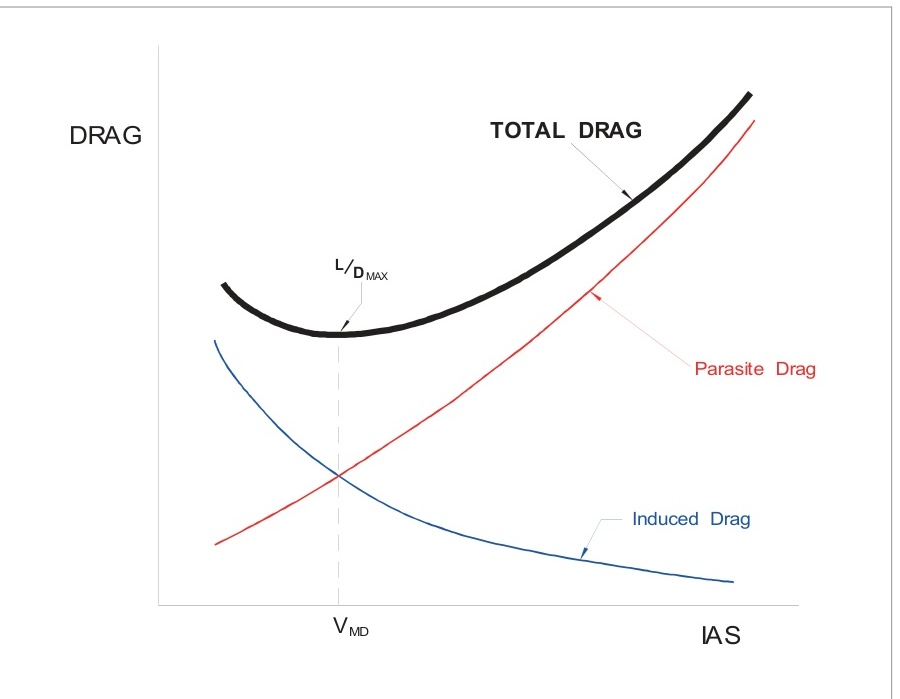
圖6.16顯示了低速時誘導阻力的主導地位和高速時寄生阻力的主導地位。由于寄生阻力和誘導阻力隨速度變化的特殊方式,總阻力最小的速度( V M D V_{MD} VMD?)出現在誘導阻力和寄生阻力相等時。最小阻力速度是飛機性能許多方面的重要參考。航程、續航時間、爬升、滑翔、機動、著陸和起飛性能都基于與飛機總阻力曲線相關的某種關系。由于在 V M D V_{MD} VMD?飛行時產生的總阻力最小(在升力等于重量的情況下),飛機也將處于 L / D M A X \mathrm {L}/\mathrm {D}_{\mathrm {MAX}} L/DMAX?迎角(約 4 ° 4^{\circ} 4°)。
重要的是要記住, L / D M A X \mathrm {L}/\mathrm {D}_{\mathrm {MAX}} L/DMAX?是在特定迎角獲得的,并且最大升阻比是衡量空氣動力學效率的指標。
注意:如果飛機在 L / D MAX L/D_{\text {MAX}} L/DMAX?迎角下運行,在產生所需升力的同時阻力將最小。任何低于或高于 L / D M A X L/D_{MAX} L/DMAX?的迎角都會增加給定升力下的阻力;更大的阻力需要更多的推力,這將是低效且昂貴的。還必須注意,如果IAS變化,L/D也會變化。
圖5.7展示了L/D比與迎角的關系圖。L/D的另一種表示方法是極坐標圖,其中 C L C_{L} CL?對 C D C_{D} CD?作圖,如圖6.17所示。
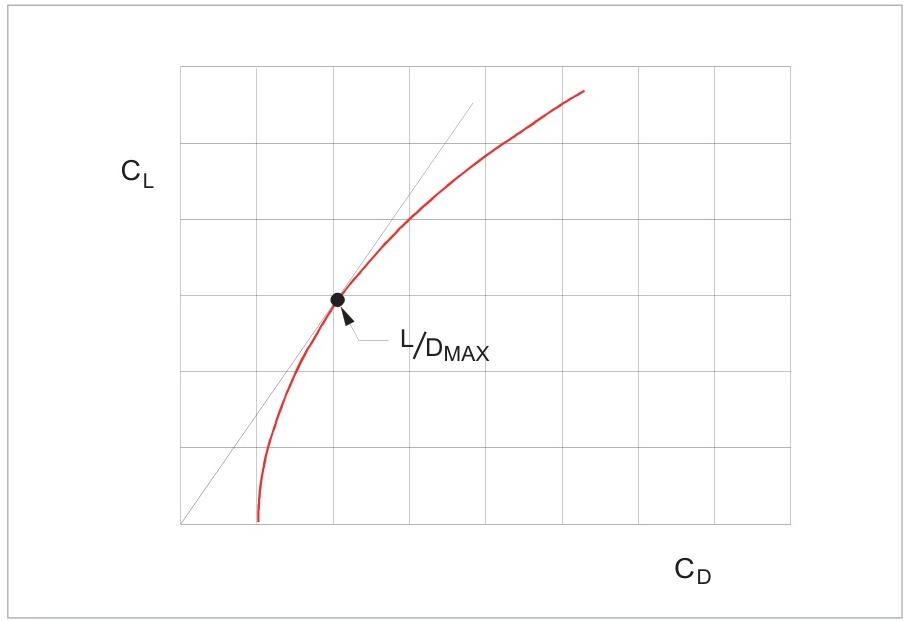
圖6.17中的 C L / C D \mathrm {C}_{\mathrm {L}}/\mathrm {C}_{\mathrm {D}} CL?/CD?整機極坐標圖顯示 C L C_{L} CL?最初增長速度遠快于 C D C_{D} CD?,但最終 C D C_{D} CD?增長更快。最大升阻比的條件可以通過從原點畫一條切線到曲線上來確定。
注意:這是顯示L/D比的非常常見的方法,因此圖6.17中的顯示應該被熟知。
飛機總重量對總阻力的影響
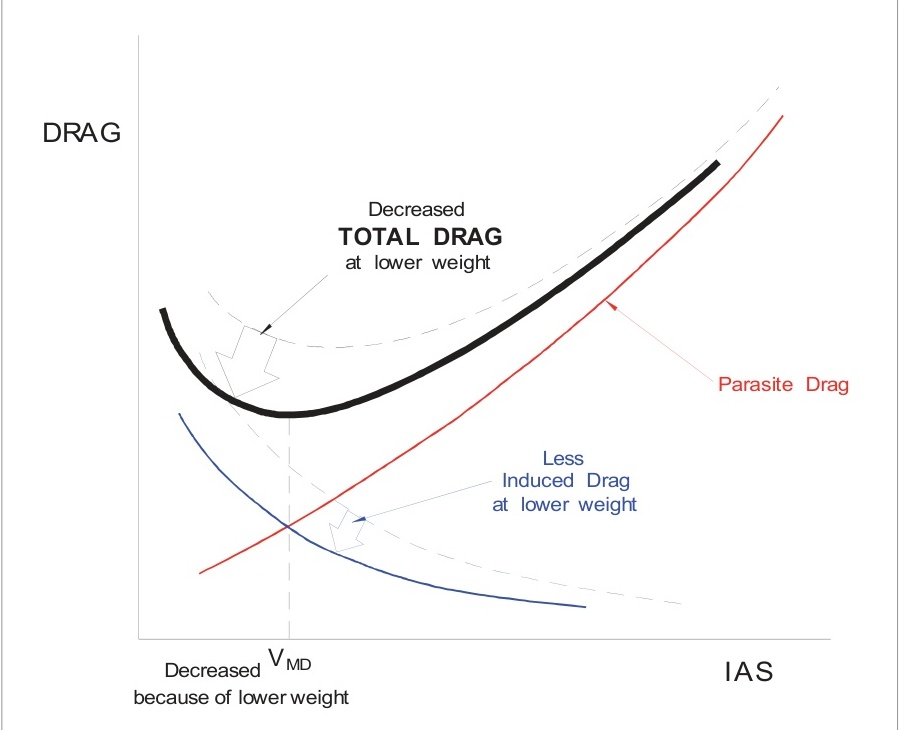
飛機總重量變化對總阻力的影響可以從圖6.18看出。隨著燃油消耗,總重量將減少。隨著飛機重量減輕,所需升力減少(較低的 C L C_L CL?),這將減少誘導阻力。總阻力將減少, V M D V_{MD} VMD?將出現在較低的IAS。
如果飛機以較高的總重量運行,將需要更多的升力。如果產生更多的升力,誘導阻力將更高,總阻力將更大, V M D V_{MD} VMD?將出現在較高的IAS。如果飛機機動使得載荷系數增加,結果將類似于總重量增加所造成的影響,即誘導阻力將增加。
高度對總阻力的影響
飛機通常在指示空速(IAS)限制范圍內運行,因此考慮阻力隨IAS的變化是有意義的。如果飛機以恒定IAS飛行,動壓將保持恒定。隨著密度隨高度增加而減小,必須增加真空速(TAS)以保持恒定的IAS( Q = 1 / 2 ρ ~ V 2 \mathrm {Q}=1/2ρ\mathrm {\sim V}^{2} Q=1/2ρ~V2)。如果飛機以恒定IAS飛行,阻力不會隨高度變化。
構型對總阻力的影響
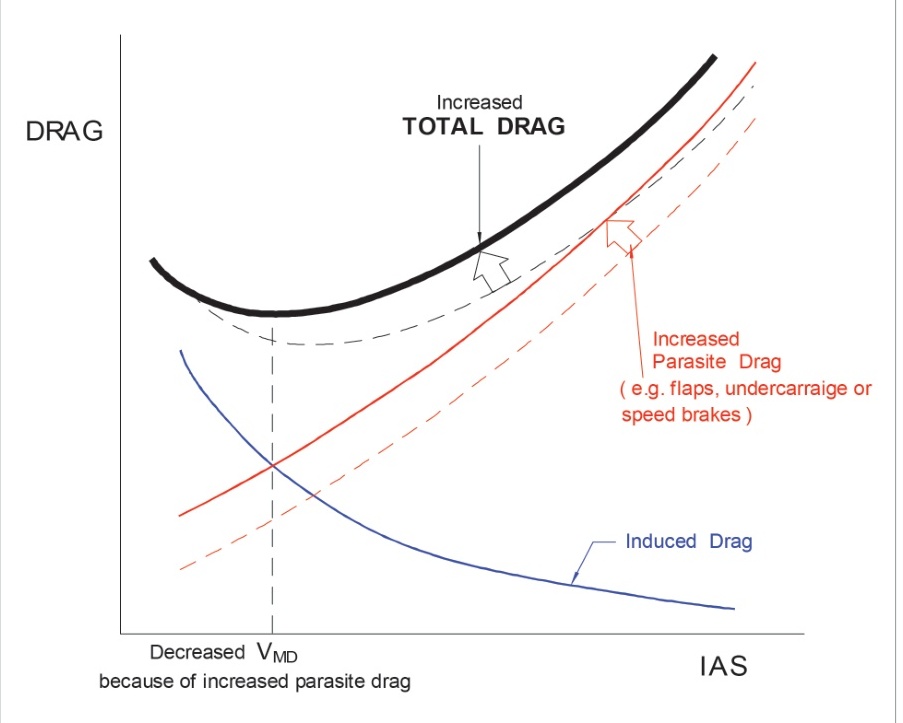
放下起落架、空氣剎車或襟翼將增加寄生阻力,但不會實質性地影響誘導阻力。增加寄生阻力的效果是增加任何IAS下的總阻力,但與干凈構型相比,減小速度 V M D V_{MD} VMD?(圖6.19)。
速度穩定性
為了使飛機處于穩定飛行狀態,飛機必須處于平衡狀態——不能有不平衡的力或力矩。當飛機調整為以穩定速度飛行時,推力和阻力相等。因此,當飛機處于穩定飛行狀態時,可以說"阻力"和"所需推力"這兩個術語具有相同的含義。
因此,作為考慮圖6.16中阻力與IAS關系的替代方法,可以用"所需推力"替代阻力。
對于處于穩定飛行狀態的飛機,如果速度發生變化而油門設置不變(稱為"可用推力"),根據調整速度,可用推力將出現過剩或不足。這種現象如圖6.20所示。
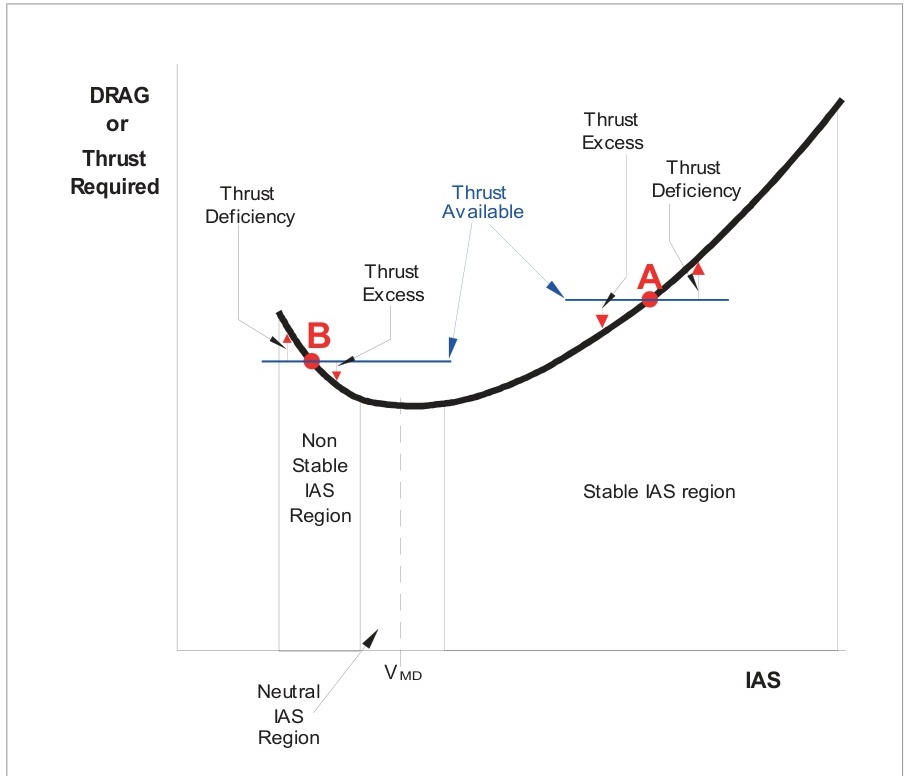
如果飛機在圖6.20中的點"A"建立穩定飛行,升力等于重量,可用推力設置為匹配所需推力。如果飛機受到干擾而速度略高于點"A",將存在推力不足;如果飛機受到干擾而速度略低于點"A",將存在推力過剩。這種關系使飛機傾向于回到點"A"的平衡狀態并恢復原始調整速度。在高于 V M D V_{MD} VMD?的速度下的穩定飛行特點是飛機自然地保持調整速度的傾向相對較強;飛機具有速度穩定性。
速度穩定性是一個重要的考慮因素,特別是在 V M D V_{MD} VMD?及以下的速度下,這在著陸進近階段最常遇到。
如果飛機在圖6.20中的點"B"建立穩定飛行,升力等于重量,可用推力設置為匹配所需推力。如果飛機受到干擾而速度高于調整速度,阻力將減小,產生推力過剩,導致飛機加速。如果干擾使飛機速度低于調整速度,阻力將增加,產生推力不足,導致飛機進一步減速。這種關系基本上是不穩定的,因為點"B"兩側的推力過剩變化傾向于放大任何原始干擾。在低于 V M D V_{MD} VMD?的速度下的穩定飛行特點是飛機傾向于偏離調整速度,飛機速度不穩定。如果干擾減小速度,它自然會繼續減小。如果干擾增加速度,它將繼續加速直到推力和阻力再次平衡。因此,飛行員必須在進近階段密切監控IAS。飛機減速的任何趨勢必須立即通過"慷慨"地使用推力來迅速回到所需的調整速度。
考慮圖6.19。如果飛機在速度不穩定區域保持恒定IAS,通過選擇放下起落架或展開襟翼增加寄生阻力的好處是減小 V M D V_{MD} VMD?,這可以通過將速度穩定區域向左移動來改善速度穩定性。
在非常接近 V M D V_{MD} VMD?的速度下,飛機通常既不表現出速度穩定性也不表現出速度不穩定性——這是中性IAS區域。
所需功率(簡介)
現在我們將考慮推力、阻力和功率之間的關系。這些聽起來像是發動機方面的考慮,可能更適合在第4冊中學習,但已經表明阻力也可以稱為"所需推力",現在你將看到與"所需功率"存在類似的關系——它們都是重要的機體考慮因素。
-
推力是一種力(推或拉),用于抵抗阻力,
但功率是做功的速率,或 功率 = 功 時間 \text {功率}=\frac {\text {功}}{\text {時間}} 功率=時間功?
且 功 = 力 × 距離 \text {功}=\text {力}×\text {距離} 功=力×距離
所以功率必須是 力 × 距離 時間 \frac {\text {力}×\text {距離}}{\text {時間}} 時間力×距離?
對于所需功率:
哪種力?
阻力。
距離除以時間是速度。
哪種速度?
唯一的速度——飛機穿過空氣的速度,真空速(TAS)。
因此:所需功率 = 阻力 × TAS
-
如果飛機以恒定IAS爬升,阻力將保持恒定,但TAS必須增加——所以所需功率將增加。
在學習飛行原理時有必要考慮所需功率,因為必須對飛機做功才能在爬升時將其"提升"到更高的高度。邏輯上,當發動機提供的可用功率最大且機體所需功率最小時,可以在最短時間內對飛機做最大功。
為便于參考,將"功率"一詞與"速率"一詞聯系起來。例如,在穩定滑翔中,當飛機以最小所需功率速度( V M P V_{MP} VMP?)飛行時,可以達到最小下降率。
這些和其他考慮因素將在第6冊的飛機性能研究和本冊第12章的飛行力學中更全面地檢查。
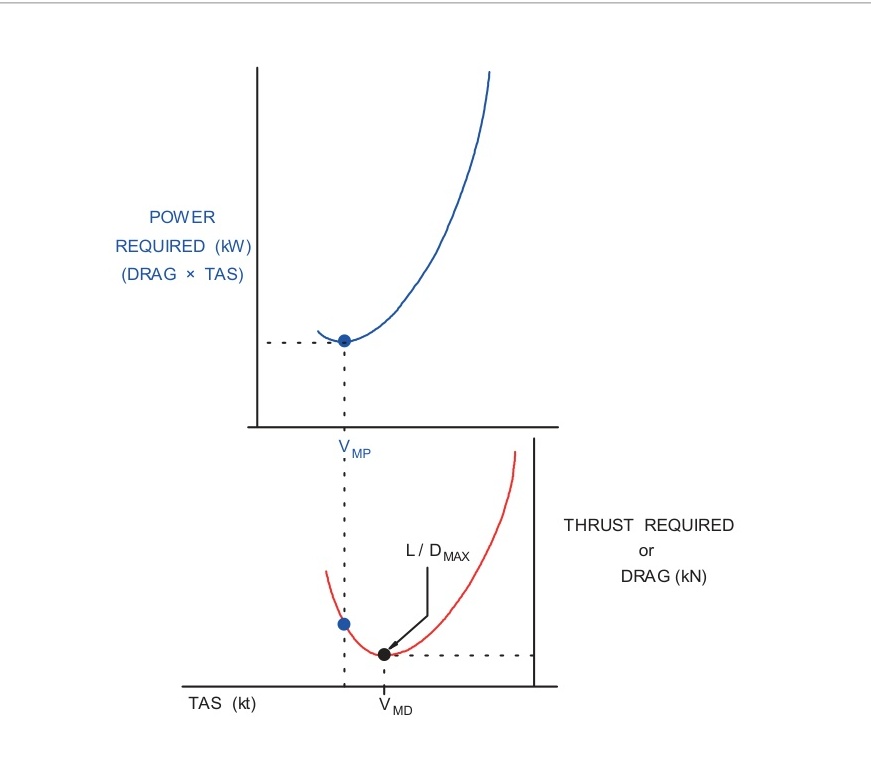
圖6.21是為海平面條件繪制的,其中 TAS=IAS \text {TAS=IAS} TAS=IAS,僅適用于一種特定飛機,一種重量,僅在平飛中,顯示了如何通過將每個阻力值乘以相應的TAS并將其轉換為千瓦來構建TAS與"所需功率"的圖表。
最小所需功率的速度稱為 V M P V_{MP} VMP?,是一個指示空速(IAS)。
注意,對應于最小所需功率的速度( V M P V_{MP} VMP?)比最小阻力速度( V M D V_{MD} VMD?)慢。
高度的影響
以 V M D V_{MD} VMD?飛行的飛機在任何高度都將經歷恒定的阻力,因為 V M D V_{MD} VMD?是一個IAS。在高空,給定IAS的TAS更高,但所需功率也增加,因為所需功率 = 阻力 × TAS。因此,TAS與所需功率的比率不受影響, V M P V_{\mathrm {MP}} VMP?將保持比 V M D V_{MD} VMD?慢。
這些信息主要涉及飛機性能,但最小所需功率速度( V M P V_{MP} VMP?)和最小阻力速度( V M D V_{MD} VMD?)的關系對于研究穩定滑翔中的下降率和下降角很重要,這在第12章中概述。
總結
寄生阻力由以下組成:
表面摩擦阻力。
形狀(壓力)阻力。
(表面摩擦阻力加形狀阻力稱為型阻。)
干擾阻力。
寄生阻力直接隨指示空速(IAS)的平方變化——速度加倍,寄生阻力增加四倍。速度減半,寄生阻力減少到四分之一。
設計師可以通過以下方式最小化寄生阻力:
流線型設計。
倒圓角。
使用層流機翼剖面。
機組人員必須確保機體,特別是機翼,不被冰、雪、泥或雪泥污染。
誘導阻力
展向氣流產生翼尖渦流。
C L \mathrm {C}_{\mathrm {L}} CL?越高(IAS越低),翼尖渦流越強。
翼尖渦流增強下洗。
增強的下洗使機翼升力向后傾斜。
機翼升力向后傾斜越大,誘導阻力越大。
誘導阻力與指示空速(IAS)的平方成反比——速度減半,誘導阻力系數( C D i C_{Di} CDi?)增加16倍,誘導阻力(D)增加4倍。速度加倍, C D i \mathrm {C}_{\mathrm {Di}} CDi?減少到十六分之一, D i D_{i} Di?減少到四分之一。
設計師可以通過以下方式最小化誘導阻力:
使用高展弦比機翼平面形狀。
使用帶有機翼扭轉和/或展向彎度變化的錐形機翼平面形狀,或者加入機翼端板、翼尖油箱、翼尖小翼或各種翼尖形狀。
總阻力
總阻力是寄生阻力和誘導阻力的總和。
當寄生阻力和誘導阻力相等時,總阻力最小。
在低IAS時,誘導阻力占主導地位。
在高IAS時,寄生阻力占主導地位。
寄生阻力和誘導阻力相等的IAS稱為最小阻力速度( V M D V_{MD} VMD?)
隨著飛行中總重量減少,誘導阻力減少,總阻力減少, V M D V_{MD} VMD?減少。
在恒定IAS下,高度對總阻力沒有影響,但隨著密度隨高度增加而減小,TAS將增加。
增加"寄生面積"的構型變化,如起落架、襟翼或減速板,會增加寄生阻力,增加總阻力并減小 V M D V_{MD} VMD?。
速度穩定性
以高于 V M D V_{MD} VMD?的穩定IAS飛行且油門設置固定的飛機將具有速度穩定性。
以 V M D V_{MD} VMD?或更慢的穩定IAS飛行且油門設置固定的飛機通常不具有速度穩定性。
如果以穩定IAS和固定油門設置在非穩定IAS區域飛行的飛機遇到使飛機減速的干擾,飛機將傾向于進一步減速;IAS將傾向于繼續減小,總阻力增加。
所需功率
V M P V_{MP} VMP?,最小"所需功率"的指示空速比最小阻力速度 V M D V_{MD} VMD?慢。
最大TAS/功率比( 1.32 V M P 1.32V_{\mathrm {MP}} 1.32VMP?)出現在 V M D V_{\mathrm {MD}} VMD?。
問題
-
如果飛機在平飛中的空速降低到最大L/D速度以下,對總阻力有什么影響?
a. 由于誘導阻力增加,阻力增加。
b. 由于誘導阻力降低,阻力減少。
c. 由于寄生阻力增加,阻力增加。
d. 由于寄生阻力降低,阻力減少。
-
通過改變機翼的迎角,飛行員可以控制飛機的:
a. 升力和空速,但不能控制阻力。
b. 升力、總重量和阻力。
c. 升力、空速和阻力。
d. 升力和阻力,但不能控制空速。
-
當總重量增加時,誘導阻力和寄生阻力之間的關系是什么?
a. 寄生阻力增加比誘導阻力多。
b. 誘導阻力增加比寄生阻力多。
c. 寄生阻力和誘導阻力同等增加。
d. 寄生阻力和誘導阻力同等減少。
-
理論上,如果飛機在平飛中的空速加倍,寄生阻力將變為:
a. 兩倍大。
b. 一半大。
c. 四倍大。
d. 四分之一大。
-
當飛機在平飛中的空速降低到最大升阻比速度以下時,飛機的總阻力:
a. 由于寄生阻力降低而減少。
b. 由于寄生阻力增加而增加。
c. 由于誘導阻力增加而增加。
d. 由于誘導阻力降低而減少。
-
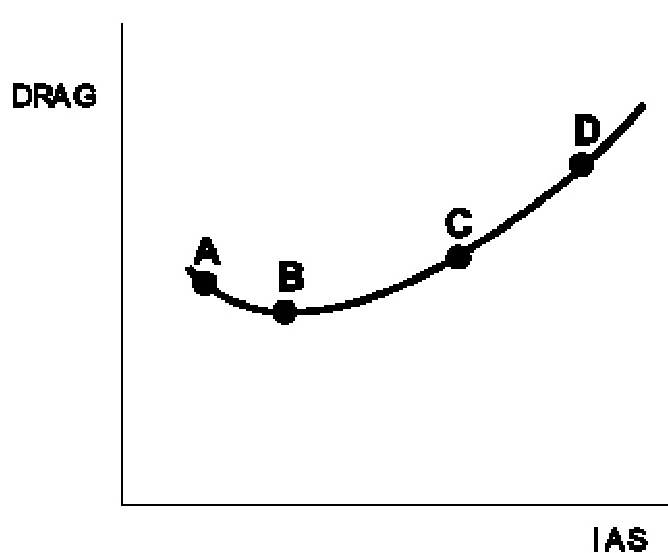
(參考附件’A’)在點B所代表的空速下,在穩定飛行中,飛機將:
a. 具有最大L/D比。
b. 具有最小L/D比。
c. 產生最大升力系數。
d. 產生最小阻力系數。
-
關于改變迎角,哪個陳述是正確的?
a. 迎角減小將增加機翼下方的壓力,并減少阻力。
b. 迎角增加將減少機翼下方的壓力,并增加阻力。
c. 迎角增加將增加阻力。
d. 迎角減小將減少機翼下方的壓力,并增加阻力。
-
在機翼上,升力作用垂直于,阻力作用平行于:
a. 飛行路徑。
b. 縱軸。
c. 弦線。
d. 縱向基準線。
-
飛機總阻力中由升力產生引起的部分稱為:
a. 誘導阻力,受空速變化的極大影響。
b. 誘導阻力,不受空速變化的影響。
c. 寄生阻力,受空速變化的極大影響。
d. 寄生阻力,與空速的平方成反比。
-
飛機的最佳L/D比出現在寄生阻力:
a. 最小時。
b. 小于誘導阻力時。
c. 大于誘導阻力時。
d. 等于誘導阻力時。
-
一架飛機在靜止空氣中以50節速度時的L/D比為15:1。在25節的正面頂風中,L/D比會是多少?
a. 30:1
b. 15:1
c. 25:1
d. 7.5:1
-
關于空氣動力學阻力,哪一項是正確的?
a. 誘導阻力是升力的副產品,受空速變化的極大影響。
b. 所有空氣動力學阻力完全由升力的產生創造。
c. 誘導阻力完全由空氣阻力創造。
d. 寄生阻力是升力的副產品。
-
在給定真空速下,增加空氣密度對飛機的升力和阻力有什么影響?
a. 升力將增加但阻力將減少。
b. 升力和阻力將增加。
c. 升力和阻力將減少。
d. 升力和阻力將保持不變。
-
如果飛機的指示空速從50節增加到100節,寄生阻力將是:
a. 四倍大。
b. 六倍大。
c. 兩倍大。
d. 四分之一大。
-
如果飛機的指示空速從100節減少到50節,誘導阻力將是:
a. 兩倍大。
b. 四倍大。
c. 一半大。
d. 四分之一大。
-
飛機在給定構型下的最佳L/D比是一個:
a. 隨指示空速變化的值。
b. 根據所攜帶的重量而變化的值。
c. 隨空氣密度變化的值。
d. 無論指示空速如何變化都保持恒定的值。
-
飛機從穩定飛行狀態被干擾時,產生使其恢復到原始狀態的力的傾向,稱為:
a. 機動性。
b. 可控性。
c. 穩定性。
d. 不穩定性。
-
隨著指示空速在平飛中增加,飛機的總阻力變得大于最大升阻比速度下產生的總阻力,這是因為:
a. 僅誘導阻力減少。
b. 誘導阻力增加。
c. 寄生阻力增加。
d. 僅寄生阻力減少。
-
空氣粘性導致的阻力或表面摩擦,當空氣沿機翼表面流過時,是一種:
a. 誘導阻力。
b. 形狀阻力。
c. 寄生阻力。
d. 干擾阻力。
-
比較阻力和空速時,哪種關系是正確的?
a. 寄生阻力與空速的平方成反比。
b. 誘導阻力隨空速的平方增加。
c. 寄生阻力隨升力系數的平方除以展弦比增加。
d. 誘導阻力與空速的平方成反比。
-
如果在地面效應中保持與地面效應外相同的迎角,升力將:
a. 減少,寄生阻力將減少。
b. 增加,誘導阻力將減少。
c. 減少,寄生阻力將增加。
d. 增加,誘導阻力將增加。
-
關于飛機在L/Dmax下的飛行,哪個陳述是正確的?
a. 任何不是L/Dmax的迎角都會增加寄生阻力。
b. 任何不是L/Dmax的迎角都會增加升阻比。
c. 任何不是L/Dmax的迎角都會增加給定飛機升力的總阻力。
d. 任何不是L/Dmax的迎角都會增加升力并減少阻力。
-
機翼的展弦比定義為:
a. 弦長的平方與翼展的比率。
b. 翼展與翼根的比率。
c. 面積的平方與弦長的比率。
d. 翼展與平均弦長的比率。
-
一個非常高展弦比的機翼(與低展弦比機翼相比)將有:
a. 在低空速下的控制品質差。
b. 在高迎角下的阻力增加。
c. 較低的失速速度。
d. 在其連接點上的彎曲力矩減少。
-
在恒定氣流速度下,高展弦比機翼(與低展弦比機翼相比)將有:
a. 增加的阻力,特別是在低迎角下。
b. 減少的阻力,特別是在高迎角下。
c. 增加的阻力,特別是在高迎角下。
d. 減少的阻力,特別是在低迎角下。
-
(參考附件’B’)哪架飛機具有最高展弦比?
a. 3。
b. 4。
c. 2。
d. 1。
-
(參考附件’B’)哪架飛機具有最低展弦比?
a. 4。
b. 2。
c. 3。
d. 1。
-
(參考附件’B’)僅考慮展弦比(其他因素保持不變)。哪架飛機將產生最大升力?
a. 1。
b. 2。
c. 3。
d. 4。
-
(參考附件’B’)僅考慮展弦比(其他因素保持不變)。哪架飛機將產生最大阻力?
a. 1。
b. 4。
c. 3。
d. 2。
-
從 C LMAX \mathbf {C}_{\text {LMAX}} CLMAX?加速到最大速度時,總阻力會發生什么變化?
a. 增加。
b. 先增加后減少。
c. 減少。
d. 先減少后增加。
-
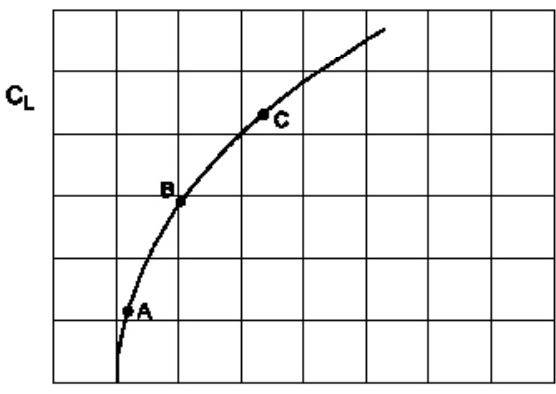
(參考附件 ′ C ′ {}^{\prime }C^{\prime } ′C′),整機 C L C_{L} CL?對 C D C_{D} CD?極坐標圖。點’B’代表:
1.最佳升阻比。
2.臨界迎角。
3.推薦進近速度。
4.永不超越速度 ( V N E ) \left(V_{NE}\right) (VNE?)
a. 1和2。
b. 僅1。
c. 2和3。
d. 僅4。
-
如果飛機在平飛中的指示空速從 100 k t 100kt 100kt增加到 200 k t 200kt 200kt,(i) TAS (ii) C D i \mathrm {C}_{\mathrm {Di}} CDi? (iii) D i D_{i} Di?將變化多少倍?
| (i) | (ii) | (iii) | |
|---|---|---|---|
| a. | 2 | 1/4 | 1/16 |
| b. | 0 | 4 | 16 |
| c. | 4 | 1/16 | 1/4 |
| d. | 2 | 1/16 | 1/4 |
附件 A
附件 B
飛機1. 翼展 22.5 米 弦長 4 米
飛機2. 機翼面積 90 平方米 翼展 45 米
飛機3. 翼展 30 米 弦長 3 米
飛機4. 機翼面積 90 平方米 翼展 40 米
附件 C
答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | c | b | c | c | a | c | a | a | d | b | a |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| b | a | b | d | c | c | c | d | b | c | d | c |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
|---|---|---|---|---|---|---|---|
| b | c | d | b | a | d | b | d |


微調技術總結)

)


)

實現)








用websocket顯示大模型的流式輸出)
