機器學習實戰，天貓雙十一銷量與中國人壽保費預測，使用多項式回歸，梯度下降，EDA數據探索，彈性網絡等技術

前言

很多同學學機器學習時總感覺：“公式推導我會，代碼也能看懂，但自己從頭做項目就懵”。

這次我們選了兩個小數據集，降低復雜度，帶大家從頭開始進行分析，建模，預測，可視化等，體驗完整流程。把多項式回歸、梯度下降、正則化等技術真正用起來，而不是只做數學題。

所有代碼用Python實現（sklearn+pandas+matplotlib），可直接在Jupyter筆記本上跑通，適合練手。

數據集較舊，學習完后可尋找最新數據集等自行訓練模型。

關注我，學習技術，一起進步！

天貓雙十一銷量預測

天貓雙十一，從2009年開始舉辦，第一屆成交額僅僅0.5億，后面呈現了爆發式的增長，那么這些增長是否有規律呢？是怎么樣的規律，該如何分析呢？我們使用多項式回歸一探究竟！

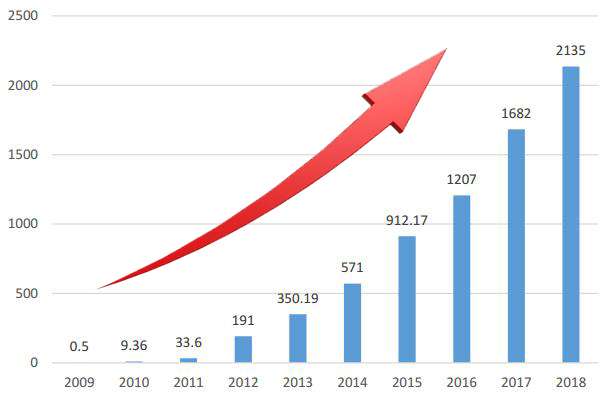
數據可視化，歷年天貓雙十一銷量數據：

import numpy as np
from sklearn.linear_model import SGDRegressor
import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 18
plt.figure(figsize=(9,6))# 創建數據，年份數據2009 ~ 2019
X = np.arange(2009,2020)
y = np.array([0.5,9.36,52,191,350,571,912,1207,1682,2135,2684])
plt.bar(X,y,width = 0.5,color = 'green')
plt.plot(X,y,color = 'red')
_ = plt.xticks(ticks = X)

有圖可知，在一定時間內，隨著經濟的發展，天貓雙十一銷量與年份的關系是多項式關系！假定，銷量和年份之間關系是三次冪關系：

import numpy as np
from sklearn.linear_model import SGDRegressor
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
plt.figure(figsize=(12,9))# 1、創建數據，年份數據2009 ~ 2019
X = np.arange(2009,2020)
y = np.array([0.5,9.36,52,191,350,571,912,1207,1682,2135,2684])# 2、年份數據，均值移除，防止某一個特征列數據天然的數值太大而影響結果
X = X - X.mean()
X = X.reshape(-1,1)# 3、構建多項式特征，3次冪
poly = PolynomialFeatures(degree=3)
X = poly.fit_transform(X)
s = StandardScaler()
X_norm = s.fit_transform(X)# 4、創建模型
model = SGDRegressor(penalty='l2',eta0 = 0.5,max_iter = 5000)
model.fit(X_norm,y)# 5、數據預測
X_test = np.linspace(-5,6,100).reshape(-1,1)
X_test = poly.transform(X_test)
X_test_norm = s.transform(X_test)
y_test = model.predict(X_test_norm)# 6、數據可視化
plt.plot(X_test[:,1],y_test,color = 'green')
plt.bar(X[:,1],y)
plt.bar(6,y_test[-1],color = 'red')
plt.ylim(0,4096)
plt.text(6,y_test[-1] + 100,round(y_test[-1],1),ha = 'center')
_ = plt.xticks(np.arange(-5,7),np.arange(2009,2021))

結論：

數據預處理，均值移除。如果特征基準值和分散度不同在某些算法（例如回歸算法，KNN等）上可能會大大影響了模型的預測能力。通過均值移除，大大增強數據的離散化程度。
多項式升維，需要對數據進行Z-score歸一化處理，效果更佳出色
SGD隨機梯度下降需要調整參數，以使模型適應多項式數據
從2020年開始，天貓雙十一統計的成交額改變了規則為11.1日~11.11日的成交數據（之前的數據為雙十一當天的數據），2020年成交額為4980億元
可以，經濟發展有其客觀規律，前11年高速發展（曲線基本可以反應銷售規律），到2020年是一個轉折點。

中國人壽保費預測

1、數據加載與介紹

import numpy as np
import pandas as pd
data = pd.read_excel('./中國人壽.xlsx')
print(data.shape)
data.head()

注意可能需要安裝庫：openpyxl

pip install openpyxl

數據介紹：

共計1338條保險數據，每條數據7個屬性
最后一列charges是保費
前面6列是特征，分別為：年齡、性別、體重指數、小孩數量、是否抽煙、所在地區

2、EDA數據探索

EDA（Exploratory Data Analysis），即探索性數據分析，是數據分析中的一個重要環節，旨在對數據進行初步的探索和分析，以發現數據的內在結構、特征、關系以及潛在的問題，為后續的數據分析和建模提供基礎。

通過 EDA，可以幫助數據分析師和機器學習工程師更好地理解數據，發現數據中的問題和規律，為制定合適的數據分析策略、選擇合適的模型以及進行有效的特征工程提供依據，從而提高數據分析和建模的準確性和可靠性。

import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt# 解決中文顯示問題
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑體字體
plt.rcParams['axes.unicode_minus'] = False  # 解決負號顯示問題# 定義一個函數來繪制不同特征對保費的影響
def plot_kde_by_feature(data, feature, ax):# 將數據轉換為長格式melted_data = pd.melt(data, id_vars=['charges'], value_vars=[feature])# 繪制核密度估計圖sns.kdeplot(data=melted_data, x='charges', fill=True, hue='value', ax=ax)ax.set_title(f'{feature}對保費的影響')# 創建一個 2x2 的子圖布局
fig, axes = plt.subplots(2, 2, figsize=(12, 10))# 性別對保費影響
plot_kde_by_feature(data, 'sex', axes[0, 0])# 地區對保費影響
plot_kde_by_feature(data, 'region', axes[0, 1])# 吸煙對保費影響
plot_kde_by_feature(data, 'smoker', axes[1, 0])# 孩子數量對保費影響
plot_kde_by_feature(data, 'children', axes[1, 1])# 調整子圖之間的間距
plt.tight_layout()
plt.show()

總結：

不同性別對保費影響不大，不同性別的保費的概率分布曲線基本重合，因此這個特征無足輕重，可以刪除
地區同理
吸煙與否對保費的概率分布曲線差別很大，整體來說不吸煙更加健康，那么保費就低，這個特征很重要
家庭孩子數量對保費有一定影響

3、特征工程

特征工程是指從原始數據中提取、轉換和選擇特征，以提高機器學習模型性能的過程。

它是數據科學和機器學習領域中至關重要的一個環節，直接影響模型的效果和效率。

特征工程的目的是為了讓數據更好地表達問題的本質，使模型能夠更準確地學習到數據中的模式和規律，從而提高模型的性能和泛化能力。

一個好的特征工程可以顯著提升模型的效果，甚至比選擇更復雜的模型更有效。

data = data.drop(['region', 'sex'], axis=1)
data.head() # 刪除不重要特征# 體重指數，離散化轉換，體重兩種情況：標準、肥胖
def convert(df,bmi):df['bmi'] = 'fat' if df['bmi'] >= bmi else 'standard'return df
data = data.apply(convert, axis = 1, args=(30,))
data.head()# 特征提取，離散型數據轉換為數值型數據
data = pd.get_dummies(data)
data.head()# 特征和目標值抽取
X = data.drop('charges', axis=1) # 訓練數據
y = data['charges'] # 目標值
X.head()

4、特征升維

特征升維是一種數據預處理技術，其核心目的是通過對原始特征進行組合、變換等操作，創造出更多的特征，從而增加數據的維度。

這有助于機器學習模型捕捉到數據中更復雜的模式和關系，尤其適用于處理線性模型難以擬合的非線性數據。

為什么需要特征升維？

在很多實際問題中，數據的特征和目標變量之間可能存在非線性關系。

然而，像線性回歸這類基礎的線性模型，只能學習到特征和目標變量之間的線性關聯。

通過特征升維，能夠讓線性模型也具備一定捕捉非線性關系的能力，進而提升模型的擬合效果和預測能力。

from sklearn.linear_model import LinearRegression
from sklearn.linear_model import ElasticNet
from sklearn.metrics import mean_squared_error,mean_squared_log_error# 數據拆分
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)# 特征升維
poly = PolynomialFeatures(degree= 2, include_bias = False)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.fit_transform(X_test)

5、模型訓練與評估

普通線性回歸：

model_1 = LinearRegression()
model_1.fit(X_train_poly, y_train)
print('測試數據得分：',model_1.score(X_train_poly,y_train))
print('預測數據得分：',model_1.score(X_test_poly,y_test))
print('訓練數據均方誤差：',np.sqrt(mean_squared_error(y_train,model_1.predict(X_train_poly))))
print('測試數據均方誤差：',np.sqrt(mean_squared_error(y_test,model_1.predict(X_test_poly))))print('訓練數據對數誤差：',np.sqrt(mean_squared_log_error(y_train,model_1.predict(X_train_poly))))
print('測試數據對數誤差：',np.sqrt(mean_squared_log_error(y_test,model_1.predict(X_test_poly))))

彈性網絡回歸：

model_2 = ElasticNet(alpha = 0.3,l1_ratio = 0.5,max_iter = 50000)
model_2.fit(X_train_poly,y_train)
print('測試數據得分：',model_2.score(X_train_poly,y_train))
print('預測數據得分：',model_2.score(X_test_poly,y_test))print('訓練數據均方誤差為：',np.sqrt(mean_squared_error(y_train,model_2.predict(X_train_poly))))
print('測試數據均方誤差為：',np.sqrt(mean_squared_error(y_test,model_2.predict(X_test_poly))))print('訓練數據對數誤差為：',np.sqrt(mean_squared_log_error(y_train,model_2.predict(X_train_poly))))
print('測試數據對數誤差為：',np.sqrt(mean_squared_log_error(y_test,model_2.predict(X_test_poly))))