參考鏈接:
范數(Norm)——定義、原理、分類、作用與應用 - 知乎
帶你秒懂向量與矩陣的范數(Norm)_矩陣norm-CSDN博客
什么是范數(norm)?以及L1,L2范數的簡單介紹_l1 norm-CSDN博客
?范數(Norm)是線性代數中的一個基本概念,用來度量一個向量的“長度”或“大小”。
(簡單來說,范數告訴我們一個向量離原點有多遠。)
- 向量范數 表征 向量空間中向量的大小,
- 矩陣范數 表征 矩陣引起變化的大小。?
在機器學習中,范數常用于:
- 衡量預測誤差(損失函數)
- 控制模型參數(正則化)
- 比較向量之間的相似度(歸一化)
不同范數對應不同的學習目標:
- L1 控稀疏;
- L2 控幅度;
- L∞ 控最大值。
引入范數的原因?
我們都知道,函數與幾何圖形往往是有對應的關系,這個很好想象,特別是在三維以下的空間內,函數是幾何圖像的數學概括,而幾何圖像是函數的高度形象化。
但當函數與幾何超出三維空間時,就難以獲得較好的想象,于是就有了映射的概念,進而引入范數的概念。當有了范數的概念,就可以引出兩個向量的距離的定義,這個向量可以是任意維數的。
通過距離的定義,進而我們可以討論逼近程度,從而討論收斂性、求極限。
- 范數在計算機領域多用于:迭代過程中收斂性質的判斷。
- 一般迭代前后步驟的差值的范數表示其大小,常用的是二范數,差值越小表示越逼近實際值,可以認為達到要求的精度,收斂。
總的來說,范數存在的意義是為了實現比較距離。
比如,在一維實數集合中,我們隨便取兩個點4和9,我們知道9比4大。
但是到了二維實數空間中,取兩個點(1,0)和(3,4),這個時候就沒法比較它們之間的大小,因為它們不是可以比較的實數。
于是引入范數這個概念,把(1,0)和(3,4)通過范數分別映射到實數1 和 5 (兩個點分別到原點的距離),這樣我們就比較這兩個點了。
所以可以看到,范數其實是一個函數,它把不能比較的向量轉換成可以比較的實數。
數學原理

向量的范數
在數學上,對于向量范數的定義,就是只要滿足以下三條性質的函數,我們就可以稱為它為范數。

(條件1的??的意思就是當且僅當的意思)
所以,范數的是一個寬泛的概念,有很多種,但是一般只會用到常用的范數。
線性代數中最有用的一些運算符是范數(norm)。 非正式地說,向量的范數是表示一個向量有多大。 這里考慮的大小(size)概念不涉及維度,而是分量的大小。
在線性代數中,向量范數是將向量映射到標量的函數?
?。 給定任意向量x,向量范數要滿足一些屬性。
性質3&4即正定,性質1即齊次,性質2即三角不等性。
向量的?L0范數
意義:非0元素個數

評價:L0范數表示向量中非零元素的個數。
L0范數的這個屬性,使其非常適用于機器學習中的稀疏編碼。
在特征選擇中,通過最小化L0范數來尋找最少最優的稀疏特征項。
但是,L0范數的最小化問題是NP難問題。而L1范數是L0范數的最優凸近似,它比L0范數要更容易求解。
因此,優化過程將會被轉換為更高維的范數(例如L1范數)問題。
向量的?L1范數 (曼哈頓范數、、最小絕對誤差)
意義:各個元素的絕對值之和(向量x中非零元素的絕對值之和)
幾何意義:實際走的 “橫+豎” 的 “城市街道” 距離。

使用?L1范數可以度量兩個向量間的差異,如絕對誤差和(Sum of Absolute Difference):

由于L1范數的天然性質,對L1優化的解是一個稀疏解,
因此L1范數也被叫做?“Lasso regularization”(稀疏規則算子)。
通過L1可以實現特征的稀疏,去掉一些沒有信息的特征,例如在對用戶的電影愛好做分類的時候,用戶有100個特征,可能只有十幾個特征是對分類有用的,大部分特征如身高體重等可能都是無用的,利用L1范數就可以過濾掉。
向量的?L2范數 (歐幾里得范數)
意義:每個元素平方和再平方根
 ?即?
?即?
像L1范數一樣,L2也可以度量兩個向量間的差異,如平方差和(Sum of Squared Difference):

評價:L2范數是最常用的范數,比如用的最多的度量距離歐氏距離就是一種L2范數。
在回歸里面,有人把加了L2范數項的回歸c稱為“嶺回歸”(Ridge Regression),有人也叫它“權值衰減(weight decay)”。
它被廣泛的應用在解決機器學習里面的過擬合問題:
- 通常被用來做優化目標函數的正則化項,防止模型為了迎合訓練集而過于復雜造成過擬合的情況,從而提高模型的泛化能力。
為什么L2范數可以防止過擬合?回答這個問題之前,我們得先看看L2范數實際上是什么。
L2范數是指向量各元素的平方和然后求平方根。我們讓L2范數的規則項最小,可以使得的每個元素都很小,都接近于0(L1范數會讓它等于0,而L2范數是接近于0),這是有很大的區別的。而越小的參數說明模型越簡單,越簡單的模型則越不容易產生過擬合現象。為什么越小的參數說明模型越簡單?
因為當限制了參數很小,實際上就限制了多項式某些分量的影響很小,即 相當于減少參數個數。
向量的?Lp范數 (一般形式)
意義:每個元素p次方和再p次方根
- L0、L1、L2 都是Lp范數的特例,分別對應P=0、1、2的情況;
- 可調節p控制范數行為(越大越趨近于L∞,即最大范數)
 ?即?
?即?
向量的 ∞范數 (最大范數)
意義:向量的 Lp范數的 p取無限大,即為向量的無窮范數,主要被用來度量向量元素的最大值。
- 取向量中最大絕對值作為長度。
- 有時用于魯棒性分析。
![]()
PS
L2范數其實就是向量的標準內積,向量的長度一定是范數,長度是范數的充分條件,但不是必要條件,也就是說,范數不一定就是向量的長度。由
長度定義的性質可知,滿足長度的定義要符合平行四邊形。
舉一個反例就可以證明非必要性:向量L1范數不滿足平行四邊形法則(A=(0,1)、B=(1,0))。
由內積決定的長度具有更豐富的幾何結構。
總結
簡單總結一下就是:
- L1范數: 為x向量各個元素絕對值之和,也叫“稀疏規則算”(Lasso regularization)。
- 比如 向量A=[1,-1,3], 那么A的L1范數為 |1|+|-1|+|3|.
- L2范數: 為x向量各個元素平方和的1/2次方(即 元素平方和的開根號)。
- L2范數又稱Euclidean范數或者Frobenius范數
- Lp范數: 為x向量各個元素絕對值p次方和的1/p次方。
使用機器學習方法解決實際問題時,通常用L1或L2范數做正則化(regularization),從而限制權值大小,減少過擬合風險。特別是在使用梯度下降來做目標函數優化時。
?L1正則化產生稀疏的權值,L2正則化產生平滑的權值為什么會這樣?
在支持向量機學習過程中,L1范數實際是一種對于成本函數求解最優的過程,因此,L1范數正則化通過向成本函數中添加L1范數,使得學習得到的結果滿足稀疏化,從而方便提取特征。
- L1范數可以使權值稀疏,方便特征提取。
- L2范數可以防止過擬合,提升模型的泛化能力。
L1和L2正則先驗分別服從什么分布
- L1是拉普拉斯分布。
- L2是高斯分布。
矩陣的范數
跟向量的范數定義類似,只不過矩陣的范數的性質比向量的范數性質多了一條相容性。
我們直接引出矩陣的范數定義:

矩陣范數的第三條性質也稱為加法相容性,第四條是乘法相容性,前提都是矩陣之間可以進行加法或乘法的運算。
矩陣的 1-范數(列模)
意義:矩陣的 列向量的和 的最大值,即?A的每列元素絕對值之和 的最大值,也稱為A的列范數。

矩陣的 2-范數(譜模)
意義:?矩陣的最大特征值的開平方,也稱譜范數。
- 特征值相當于是兩個維度的壓縮,相當于是從矩陣的維度里面找到最大的。

矩陣的 ∞范數(行模)
意義:矩陣的 行向量的和 的最大值,即?A的每行元素絕對值之和 的最大值,也稱為A的行范數。

矩陣的 F-范數
意義:Frobenius范數,即矩陣元素絕對值的平方和再開平方。類似于向量的L2范數。
 ?即?
?即?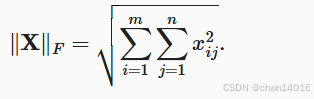
也可以描述為:

總結
簡單總結一下就是:
- L1范數: 列范數,矩陣的 列向量的和 的最大值,即?A的每列元素絕對值之和 的最大值。
- L2范數:
?矩陣的最大特征值的開平方,也稱譜范數。
- 特征值相當于是兩個維度的壓縮,相當于是從矩陣的維度里面找到最大的。
- L∞范數: 行范數,矩陣的 行向量的和 的最大值,即?A的每行元素絕對值之和 的最大值。
- Lf范數: Frobenius范數,類似于向量的L2范數,矩陣元素平方和再開平方。
范數的作用
| 作用領域 | 用途 | 說明 |
|---|---|---|
| 向量距離 | 度量兩個點或向量之間的“距離” | 用于損失函數、相似度計算 |
| 模型正則化 | 控制模型復雜度,防止過擬合 | 通過懲罰大參數避免學習噪聲 |
| 向量歸一化 | 把向量縮放到單位長度 | 常用于余弦相似度比較 |
| 稀疏表示 | 用最少的非零值表達信息 | L1 正則可自動“篩選特征” |
在機器學習中的實際應用
? 1. 損失函數中的誤差度量
| 類型 | 范數 | 說明 |
|---|---|---|
| MAE(平均絕對誤差) | L1 | 魯棒,對異常值不敏感 |
| MSE(均方誤差) | L2 | 常用,懲罰大誤差更重 |
? 2. 模型正則化(Regularization)
| 類型 | 正則項 | 功能 |
|---|---|---|
| L1 正則(Lasso) | (\lambda \sum | \theta_i |
| L2 正則(Ridge) | λ∑θi2\lambda \sum \theta_i^2 | 緩和過擬合,不會讓參數變0,但壓小 |
? 3. 向量歸一化(Normalization)

? 4. 稀疏建模(Sparse Modeling)
- 在某些應用中,希望模型只依賴少數幾個特征(稀疏性):
- 如文本分類、基因數據分析;
使用 L1 正則可以“自動讓不重要的參數變成 0”;
- L1 是稀疏性建模的核心工具。
面試范數相關常見提問匯總 + 答題思路
? 一、基礎概念類問題(定義 + 原理)
?Q1:解釋一下什么是范數嗎?
答題思路:
范數是一種用來衡量向量“大小”或“長度”的函數,它在機器學習中用于表示誤差、距離、向量歸一化或正則化。常見的范數有 L1 范數、L2 范數等,分別對應不同的應用需求。
?Q2:L1 范數和 L2 范數的區別是什么?你更偏向哪一個?
答題思路:
- L1 范數是所有元素的絕對值之和,鼓勵模型稀疏;
- L2 范數是所有元素平方和的平方根,鼓勵整體平滑;
- 如果任務要求模型可解釋性強、特征選擇重要,我會選擇 L1;
- 如果任務對穩定性更敏感,比如圖像處理,我傾向 L2。
? 二、應用場景類問題(結合模型/正則)
?Q3:在損失函數中為什么有時使用 L1 有時使用 L2?
答題思路:
- L1(如 MAE)更穩健,適合對異常值敏感的任務;
- L2(如 MSE)更常見,對大誤差懲罰更重;
- 如果數據中有 outlier,建議使用 L1;
- 如果更關注整體誤差穩定性,可以使用 L2。
?Q4:正則化中 L1 和 L2 分別起什么作用?
答題思路:
- L1 正則通過絕對值懲罰,會使某些參數收縮為 0,實現特征選擇;
- L2 正則通過平方懲罰,防止參數過大,減少過擬合;
- L1 更適合用于高維稀疏建模(如文本分類),L2 更適合神經網絡等連續模型。
? 三、原理理解類問題(深入推導)
?Q5:為什么 L2 正則不產生稀疏性,但 L1 會?
答題思路:
- 從幾何角度講,L1 范數的等值線是菱形,容易與損失函數的最優點交于坐標軸;
- 而 L2 范數的等值線是圓形,更傾向于“均勻縮小所有參數”而不是讓某些為 0;
- 所以 L1 更容易“壓掉”不重要的特征,讓參數變為0。
?Q6:你知道范數與梯度下降優化的關系嗎?
答題思路:
- 在添加正則化的損失函數中,比如 L2,會影響梯度更新方向;
- L2 會加上 λθ\lambda \theta 項,等于對參數有一個“縮小”的趨勢;
- L1 的梯度是非連續的(不可導點),所以常用次梯度或特殊優化方法處理。
? 四、項目/實踐類問題(結合實際應用)
?Q7:在項目中有沒有用到范數?怎么選的 L1 / L2?
答題思路(舉例):
- “在我做房價預測項目中,我使用了 L1 正則化進行特征選擇,發現有多個冗余特征被自動歸零,提升了模型解釋性。”
- “而在另一個圖像復原項目中,我使用了 L2 損失函數和 L2 正則,因為目標是盡可能還原每個像素值,不允許過大偏差。”
?Q8:若模型過擬合了,會怎么用范數應對?
答題思路:
- 我會通過添加正則化項(L1/L2)來約束模型參數的規模;
- 如果模型很復雜,特征維度很高,我會嘗試 L1 來讓模型自動做特征選擇;
- 如果我關注模型的穩定性和泛化性能,我會使用 L2 控制參數幅度。
? 五、開放性問題(考察綜合素質)
?Q9:如果我說 L2 正則是控制模型復雜度的“軟剪枝”,你怎么理解?
答題思路:
- 軟剪枝指的是“不強制為0,而是控制其變小”;
- L2 不會像 L1 一樣使參數歸零,但會持續壓縮大的權重;
- 這有助于模型在保持全部特征的情況下減少過擬合。
快速知識卡片(可打印記憶)
| 項 | L1 范數 | L2 范數 |
|---|---|---|
| 公式 | (\sum | x_i |
| 名稱 | 曼哈頓距離 | 歐幾里得距離 |
| 特點 | 稀疏、魯棒 | 平滑、常用 |
| 正則化應用 | Lasso(特征選擇) | Ridge(穩定優化) |
| 適用場景 | 高維稀疏建模 | 連續模型控制復雜度 |
| 損失函數 | MAE | MSE |
| 面試關鍵詞 | 特征選擇、正則稀疏性 | 權重控制、余弦相似度歸一化 |




















