注:本文為 “線性代數 | 知識點整理” 相關文章合輯。
因 csdn 篇幅合并超限分篇連載,本篇為 Ref 1。
略作重排,未整理去重。
圖片清晰度限于引文原狀。
如有內容異常,請看原文。
線性代數知識匯總
Arrow 于 2016-11-27 16:27:57 發布
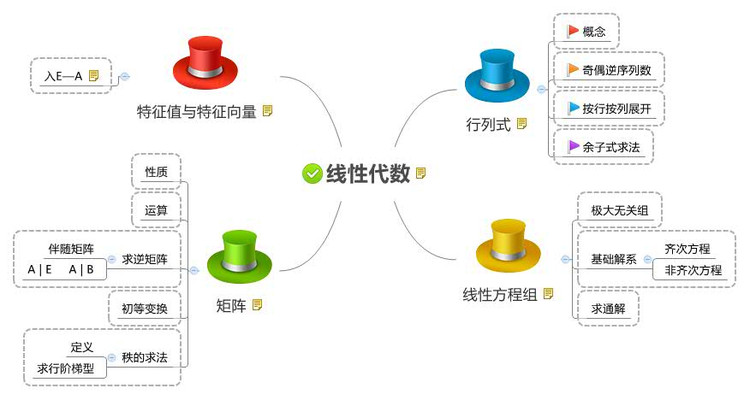
1. 線性代數知識圖譜
線性代數是 代數學 的一個分支,主要處理線性關系問題。線性關系即數學對象之間的關系是以一次形式來表達的。例如,在解析幾何里,平面上直線的方程是二元一次方程;空間平面的方程是三元一次方程,而空間直線視為兩個平面相交,由兩個三元一次方程所組成的方程組來表示。含有 n n n 個未知量的一次方程稱為線性方程。變量的一次函數稱為線性函數。線性關系問題簡稱線性問題。解線性方程組的問題是最簡單的線性問題。
線性(linear)指量與量之間按比例、成直線的關系,在數學上可以理解為一階導數為常數的函數。
非線性(non-linear)則指不按比例、不成直線的關系,一階導數 不為常數。
行列式非零 ? \Leftrightarrow ? 矩陣可逆 ? \Leftrightarrow ? 方陣滿秩 ? \Leftrightarrow ? 向量組滿秩(向量個數等于維數)。
2. 行列式
2.1 定義
矩陣的行列式,determinate(簡稱 det),是基于矩陣所包含的行列數據計算得到的一個標量。是為求解線性方程組而引入的。
2.2 二階行列式
計算方式:對角線法則
2.3 三階行列式
計算方式:對角線法則
2.4 n 階行列式
2.4.1 計算排列的逆序數
2.4.2 計算 n 階行列式
2.4.3 簡化計算總結
2.4.4 行列式的 3 種表示方法
2.5 行列式的性質
性質 1:行列式與它的轉置行列式相等。
注:行列式中行與列具有同等的地位,行列式的性質凡是對行成立的對列也同樣成立。
性質 2:互換行列式的兩行(列),行列式變號。
推論:如果行列式有兩行(列)完全相同,則此行列式為零。
性質 3:行列式的某一行(列)中所有的元素都乘以同一個倍數 k,等于用數 k 乘以此行列式。
推論:行列式的某一行(列)中所有元素的公因子可以提到行列式符號的外面。
性質 4:行列式中如果有兩行(列)元素成比例,則此行列式為零。
性質 5:若行列式的某一列(行)的元素都是兩數之和,則等于對應的兩個行列式之和。
性質 6:把行列式的某一列(行)的各元素乘以同一個倍數然后加到另一列(行)對應的元素上去,行列式不變。
2.6 計算行列式的方法
-
利用定義
-
利用性質把行列式化為上三角形行列式,從而算得行列式的值
定理中包含著三個結論:
-
方程組有解(解的存在性)。
-
解是唯一的(解的唯一性)。
-
解可以由公式 (2 =700x) 給出。
定理 4:如果線性方程組 (1 =700x) 的系數行列式不等于零,則該線性方程組一定有解,而且解是唯一的。
定理 4′:如果線性方程組無解或有兩個不同的解,則它的系數行列式必為零。
齊次線性方程組的相關定理
定理 5:如果齊次線性方程組的系數行列式 D 不等于 0,則齊次線性方程組只有零解,沒有非零解。
定理 5′:如果齊次線性方程組有非零解,則它的系數行列式必為零。
- 用克拉默法則解線性方程組的兩個條件
1 =700x) 方程個數等于未知量個數。
2 =700x) 系數行列式不等于零。
- 克拉默法則的意義主要在于建立了線性方程組的解和已知的系數以及常數項之間的關系。它主要適用于理論推導。
2.8 行列式按行(列)展開
對角線法則只適用于二階與三階行列式。
本節主要考慮如何用低階行列式來表示高階行列式。
3. 矩陣
3.1 矩陣的定義
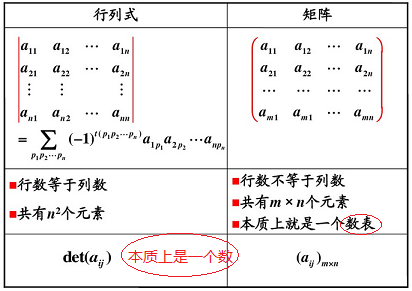
3.1.1 矩陣與行列式的區別
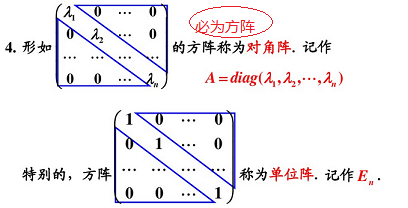
3.2 特殊矩陣
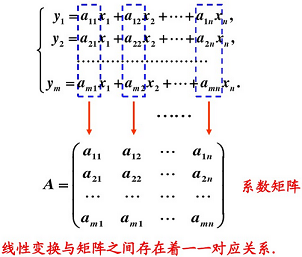
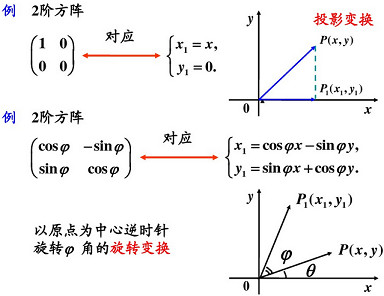
3.3 矩陣與線性變換
3.4 矩陣的運算
3.4.1 矩陣的加法
行列式與矩陣加法的比較:
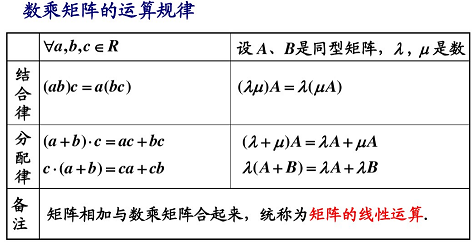
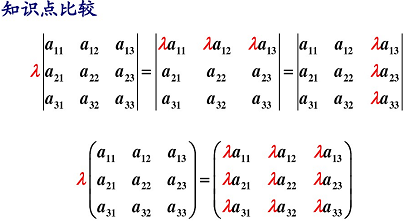
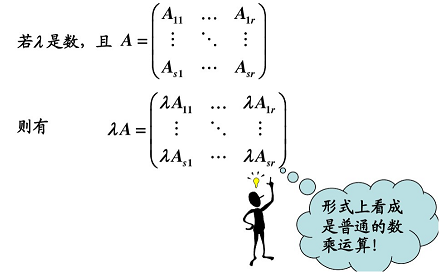
3.4.2 數乘矩陣
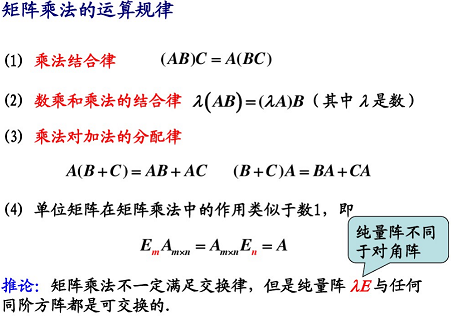
3.4.3 矩陣與矩陣相乘
3.4.4 矩陣的轉置
反對稱矩陣(skew symmetric matrix)
3.4.5 方陣的行列式
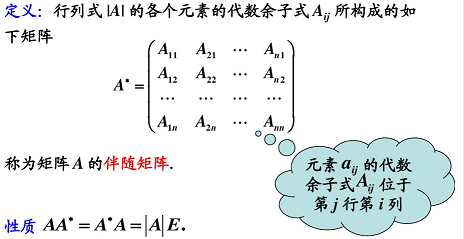
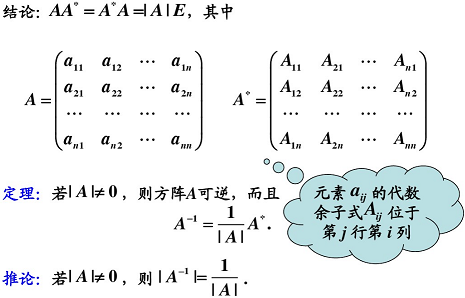
3.4.6 伴隨矩陣
3.4.7 共軛矩陣
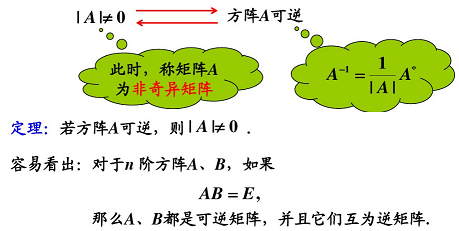
3.5 可逆矩陣(或稱非奇異矩陣)
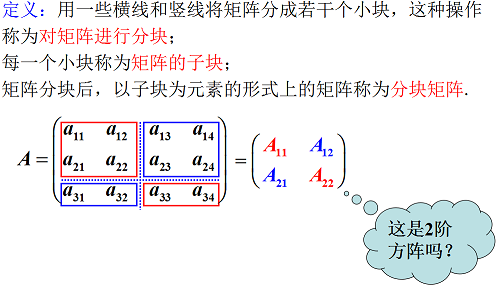
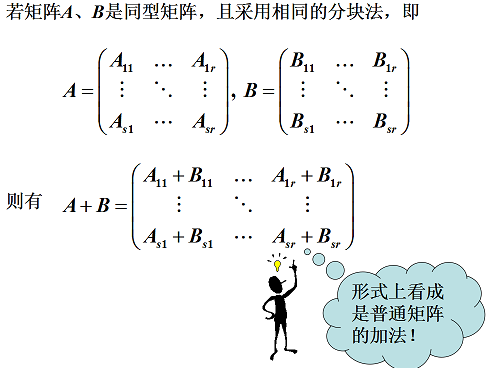
3.6 矩陣分塊法
分塊矩陣不僅形式上進行轉置,而且每一個子塊也進行轉置。
4. 矩陣的初等變換與線性方程組
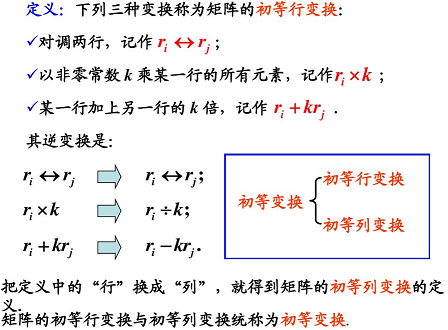
4.1 矩陣的初等變換
4.2 矩陣之間的等價關系
4.3 初等變換與矩陣乘法的關系
4.4 矩陣的秩
4.5 線性方程組的多解
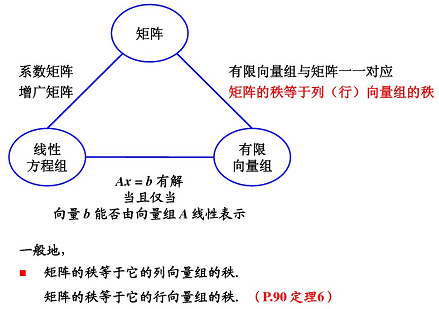
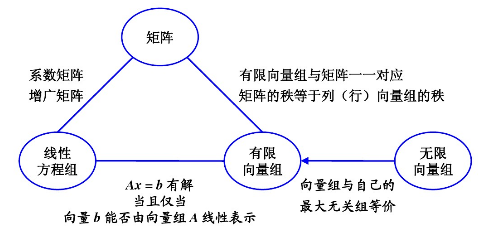
4. 向量組的線性相關性
4.1 向量組及其線性組合
4.2 向量組的線性相關性
4.3 向量組的秩
結論:矩陣的最高階非零子式一般不是唯一的,但矩陣的秩是唯一的。
4.4 線性方程組的解的結構
問題:什么是線性方程組的解的結構?
答:所謂線性方程組的解的結構,就是當線性方程組有無限多個解時,解與解之間的相互關系。
備注:
-
當方程組存在唯一解時,無須討論解的結構。
-
下面的討論都是假設線性方程組有解。
4.5 向量空間
4.5.1 封閉的概念
定義:所謂封閉,是指集合中任意兩個元素作某一運算得到的結果仍屬于該集合。
4.5.2 向量空間的概念
定義:設 V V V 是 n n n 維向量的集合,如果
① 集合 V V V 非空,
② 集合 V V V 對于向量的加法和乘數兩種運算封閉,
具體地說,就是:
若 a ∈ V a \in V a∈V, b ∈ V b \in V b∈V,則 a + b ∈ V a + b \in V a+b∈V。(對加法封閉)
若 a ∈ V a \in V a∈V, l ∈ R l \in R l∈R,則 l a ∈ V l a \in V la∈V。(對乘數封閉)
那么就稱集合 V V V 為向量空間。
4.5.3 子空間的概念
定義:如果向量空間 V V V 的非空子集合 V 1 V1 V1 對于 V V V 中所定義的加法及乘數兩種運算是封閉的,則稱 V 1 V1 V1 是 V V V 的子空間。
4.5.4 向量空間的基的概念
5. 相似矩陣及二次型
5.1 向量的內積、長度及正交性
5.1.1 向量的內積
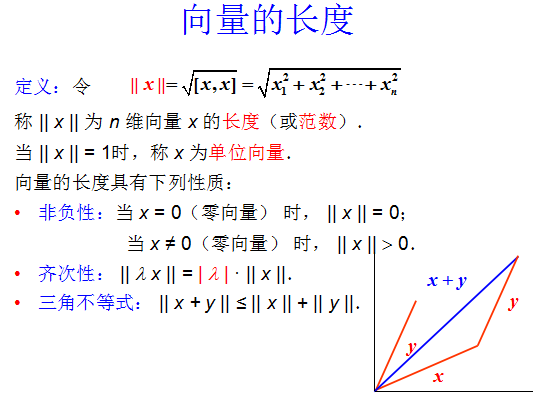
5.1.2 向量的長度或范數
單位向量:長度為 1 的向量。
5.1.3 向量的正交性
向量正交:向量內積為 0。
5.1.4 正交矩陣或正交陣
5.1.5 正交矩陣的性質
5.2 方陣的特征值與特征向量
5.2.1 正定矩陣 / 半正定矩陣
-
矩陣半 正定 當且僅當它的每個 特征值 大于等于零(>=0)。
-
矩陣正定當且僅當它的每個特征值都大于零(>0)。
5.3 相似矩陣
5.4 對稱矩陣的對角化
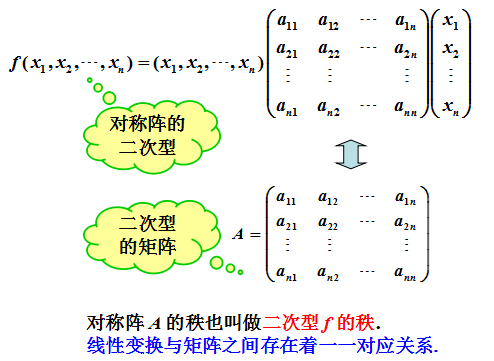
5.5 二次型及其它標準型
線性代數知識點整理
圓氣鹿醬 于 2020-10-04 23:51:23 發布
矩陣等價與矩陣相似
等價:A 經過一系列初等變換等到 B,稱 A 與 B 等價,也就是存在可逆陣 P、Q 使 B = P A Q B=PAQ B=PAQ,那么 A、B 秩相等。
相似:在線性代數中,相似矩陣是指存在相似關系的矩陣。設 A,B 為 n 階矩陣,如果有 n 階可逆矩陣 P 存在,使得 P ? 1 A P = B P^{-1} AP=B P?1AP=B,則稱矩陣 A 與 B 相似,記為 A ~ B A \sim B A~B。
相似矩陣的特點:
- 兩者的秩相等。
- 兩者的行列式值相等。
- 兩者擁有同樣的特征值,盡管相應的特征向量一般不同。
- 兩者擁有同樣的特征多項式。
行列式計算技巧
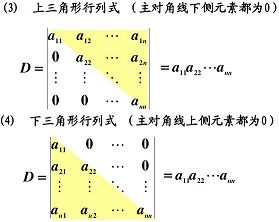
- 上三角行列式的值為主對角線數字乘積。
矩陣的初等變換與行列式值的關系
第一類初等變換(換行換列)使行列式變號,第二類初等變換(某行或某列乘 k 倍)使行列式變 k 倍,第三類初等變換(某行(列)乘 k 倍加到另一行(列))使行列式不變。
矩陣的特征值(特征根)和特征向量
-
A 必須是方陣。
-
A α = λ α A\alpha = \lambda\alpha Aα=λα( λ \lambda λ 可以為 0,特征向量 α \alpha α 是非 0 列向量)。
-
一個特征值可以對應多個特征向量,一個特征向量只能對應一個特征值。
-
特征多項式: ∣ A ? λ E ∣ |A - \lambda E| ∣A?λE∣。
-
特征方程: ∣ A ? λ E ∣ = 0 |A - \lambda E| = 0 ∣A?λE∣=0。
-
λ \lambda λ 是 A 的特征值, α \alpha α 是對應的特征向量,則 c α c\alpha cα 也是對應的特征向量( c ≠ 0 c \ne 0 c=0)。
-
α 1 , α 2 \alpha_1, \alpha_2 α1?,α2? 是 λ \lambda λ 的特征向量,則 c 1 α 1 + c 2 α 2 c_1\alpha_1 + c_2\alpha_2 c1?α1?+c2?α2? 也是特征向量(前提是同一個特征值)。
-
在解特征方程的時候若出現 ( λ ? 2 ) ( λ ? 1 ) ( λ ? 1 ) = 0 (\lambda - 2)(\lambda - 1)(\lambda - 1) = 0 (λ?2)(λ?1)(λ?1)=0,結論寫成 A 的特征值為 λ 1 = 2 , λ 2 = λ 3 = 2 \lambda_1 = 2, \lambda_2 = \lambda_3 = 2 λ1?=2,λ2?=λ3?=2(重根要寫出來)。
-
不同特征根的特征向量是線性無關的。
-
若 n 階方陣 A 可以相似于一個 n 階對角矩陣,則稱 A 可對角化,n 階方陣 A 相似于對角矩陣的充要條件是 A 有 n 個線性無關的特征向量。
-
特征值為 0,則行列式的值為 0。
-
特征值正是使得 ∣ λ E ? A ∣ = 0 | \lambda E - A| = 0 ∣λE?A∣=0 的那些根(可以用來一眼看出特征值)。
-
特征向量的求法: ( A ? λ E ) α = 0 (A - \lambda E)\alpha = 0 (A?λE)α=0。
-
特征值的積為行列式的值。
-
特征值的和為矩陣的跡。
-
特征值和特征向量的性質:
-
轉置后特征值不變。
-
設 λ \lambda λ 是 A 的特征值, λ k \lambda^k λk 是 A k A^k Ak 的特征值。
-
f ( λ ) = a 0 + a 1 λ + ? + a m λ m f(\lambda) = a_0 + a_1\lambda + \cdots + a_m\lambda^m f(λ)=a0?+a1?λ+?+am?λm 是 f ( A ) = a 0 E + a 1 A + ? + a m A m f(A) = a_0E + a_1A + \cdots + a_mA^m f(A)=a0?E+a1?A+?+am?Am 的特征值。
-
λ \lambda λ 是可逆方陣 A 的特征值, 1 λ \frac{1}{\lambda} λ1? 是 A ? 1 A^{-1} A?1 的特征值。
-
逆矩陣與伴隨矩陣與原來的矩陣有相同的特征向量。
-
矩陣和的特征值等于特征值的和。
方陣的行列式
-
∣ k A ∣ = k n ∣ A ∣ |kA| = k^n|A| ∣kA∣=kn∣A∣(因為 k A kA kA 是用 k k k 乘 A A A 里面的所有數)。
-
∣ A B C ∣ = ∣ A ∣ ∣ B ∣ ∣ C ∣ |ABC| = |A||B||C| ∣ABC∣=∣A∣∣B∣∣C∣(A、B、C 同階方陣)。
伴隨矩陣與逆矩陣
-
求伴隨矩陣(任意方陣都有伴隨矩陣):
-
求出所有元素的代數余子式。
-
按行求的代數余子式按列放構成矩陣 A ? A^* A?。
-
-
一個方陣與其伴隨矩陣的秩的關系:
-
若 R ( A ) = n R(A) = n R(A)=n, R ( A ? ) = n R(A^*) = n R(A?)=n。
-
若 R ( A ) = n ? 1 R(A) = n - 1 R(A)=n?1, R ( A ? ) = 1 R(A^*) = 1 R(A?)=1。
-
若 R ( A ) < n ? 1 R(A) < n - 1 R(A)<n?1, R ( A ? ) = 0 R(A^*) = 0 R(A?)=0(即伴隨矩陣為零矩陣)。
-
-
逆矩陣:
-
對角矩陣的逆矩陣為各元素的倒數。
-
A B = A C AB = AC AB=AC, B = C B = C B=C 的條件是 A A A 為可逆矩陣,因為左乘 A A A 的逆即可。
-
逆矩陣的行列式為原矩陣的倒數。
-
逆矩陣的特征值也為原矩陣的倒數。
-
-
A A ? = A ? A = ∣ A ∣ E AA^* = A^*A = |A|E AA?=A?A=∣A∣E。
- 當 ∣ A ∣ ≠ 0 |A| \ne 0 ∣A∣=0, ∣ A ? ∣ = ∣ A ∣ n ? 1 |A^*| = |A|^{n - 1} ∣A?∣=∣A∣n?1。
-
( A ? ) ? 1 = A ∣ A ∣ (A^*)^{-1} = \frac{A}{|A|} (A?)?1=∣A∣A?。
- ( λ A ) ? 1 = 1 λ A ? 1 (\lambda A)^{-1} = \frac{1}{\lambda} A^{-1} (λA)?1=λ1?A?1。
向量間的線性關系
-
零向量可被任一向量組表示, k k k 全取 0。
-
含零向量的任意向量組必線性相關。
-
一個零向量必相關,一個非零向量必無關。
-
一個向量組中,部分線性相關則整體線性相關。整體組線性無關,則部分線性無關。
-
線性無關的向量組,其接長向量組也無關。
-
線性相關的向量組,其截短向量組也相關。
-
n n n 個 n n n 維向量, D ≠ 0 D \ne 0 D=0,則線性無關。
-
D = 0 D = 0 D=0,線性相關。(都是充要條件)
-
若向量組 A A A: a 1 , a 2 , … , a m a_1, a_2, \ldots, a_m a1?,a2?,…,am? 線性無關,向量組 B B B: a 1 , a 2 , a 3 , … , a m , b a_1, a_2, a_3, \ldots, a_m, b a1?,a2?,a3?,…,am?,b 線性相關,則向量 b b b 必能由向量組 A A A 線性表示,且表示法唯一。
-
向量 B B B 能由向量組 A A A 線性表示,則 A A A 的秩大于等于 B B B 的秩。
向量組的秩(非 0 子式的最高階數)
-
極大線性無關組 A 0 A_0 A0? 定義:
-
向量組 A 0 A_0 A0?: a 1 , a 2 , … , a r a_1, a_2, \ldots, a_r a1?,a2?,…,ar? 線性無關。
-
A A A 中的任何向量均可由向量組 A 0 A_0 A0?: a 1 , a 2 , a 3 , … , a r a_1, a_2, a_3, \ldots, a_r a1?,a2?,a3?,…,ar? 線性表示。
-
-
極大線性無關組:
-
一個線性無關的向量組其極大線性無關組是本身。
-
任何一個向量組和它的極大線性無關組等價。
-
極大線性無關組中所含向量個數為矩陣的秩。
-
-
零向量的秩為 0。
-
KaTeX parse error: Can't use function '\)' in math mode at position 16: r(A) \leq \min(\?)?向量的個數,向量的維數)$。
-
r ( A B ) ≤ min ? ( r ( A ) , r ( B ) ) r(AB) \leq \min(r(A), r(B)) r(AB)≤min(r(A),r(B))。
-
max ? ( R ( A ) , R ( B ) ) ≤ R ( A , B ) ≤ R ( A ) + R ( B ) \max(R(A), R(B)) \leq R(A, B) \leq R(A) + R(B) max(R(A),R(B))≤R(A,B)≤R(A)+R(B)。
-
R ( A + B ) ≤ R ( A ) + R ( B ) R(A + B) \leq R(A) + R(B) R(A+B)≤R(A)+R(B)。
-
初等行變換不改變列向量的線性關系。
-
一個向量乘可逆矩陣,秩不變。
非齊次和齊次線性方程組有解判定
-
線性方程組的向量表示形式
x 1 α 1 + x 2 α 2 + x 3 α 3 + ? = β x_1\alpha_1 + x_2\alpha_2 + x_3\alpha_3 + \cdots = \beta x1?α1?+x2?α2?+x3?α3?+?=β
-
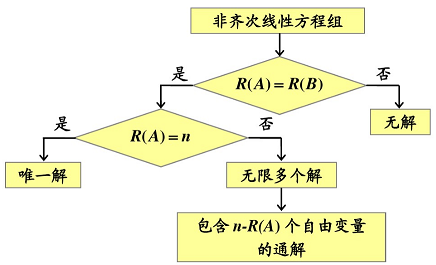
線性方程組有解判定( n n n 是未知量的個數)(不齊次的情況,即 A x = b Ax = b Ax=b( b ≠ 0 b \ne 0 b=0))
r ( a ˉ ) = r ( a ) r(\bar{a}) = r(a) r(aˉ)=r(a) 時,方程組有解,等于 n n n 有一個解;小于 n n n 有無窮多解; r ( a ˉ ) ≠ r ( a ) r(\bar{a}) \ne r(a) r(aˉ)=r(a),無解。
-
A x = 0 Ax = 0 Ax=0 有解判定( m m m 為方程個數)
r ( A ) ≤ min ? ( n , m ) r(A) \leq \min(n, m) r(A)≤min(n,m)。
當 m < n m < n m<n 時,一定有無窮多解,即有非零解。
-
基礎解系一定是線性無關的,并且是解向量的極大線性無關組,即每一個解向量都可以由基礎解系表示。
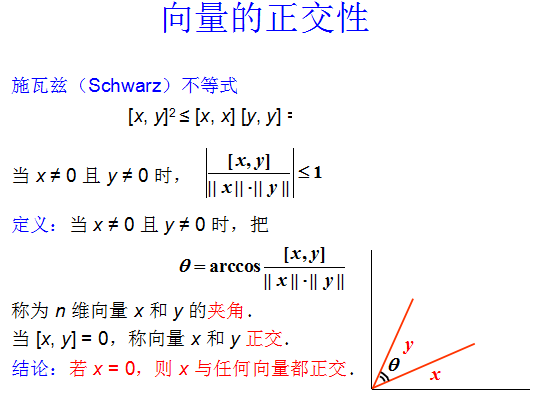
正交向量
-
x x x, y y y 內積為 0 時稱為正交(或垂直)。
-
若一個向量組中任意兩個向量都正交,則稱此向量組為正交向量組,若一個向量組中每一個向量都是單位向量,則稱此向量組為正交規范向量組或標準正交向量組。
-
實矩陣是指矩陣中每個數都是實數的矩陣。
-
A A T = E A A^T = E AAT=E 或 A T A = E A^T A = E ATA=E,則 n n n 階實矩陣 A A A 稱為正交矩陣。 A A A 為正交矩陣的充要條件是 A A A 的行(列)向量組為正交規范向量組。
-
正交矩陣的性質:
-
∣ A ∣ ∣ A T ∣ = 1 |A| |A^T| = 1 ∣A∣∣AT∣=1,所以 ∣ A ∣ = 1 |A| = 1 ∣A∣=1 或 -1。
-
若 n n n 階方陣滿足 A A T = E AA^T = E AAT=E(即 A ? 1 = A T A^{-1} = A^T A?1=AT),稱 A A A 為正交矩陣。
-
其次線性方程組解的結構
-
基礎解系解的個數是 n ? r n - r n?r 個。
-
A x = 0 Ax = 0 Ax=0
A = ( α 1 , α 2 , α 3 ) A = (\alpha_1, \alpha_2, \alpha_3) A=(α1?,α2?,α3?)
x = ( 1 , 2 , 3 ) T x = (1, 2, 3)^T x=(1,2,3)T 的實質是 α 1 + 2 α 2 + 3 α 3 = 0 \alpha_1 + 2\alpha_2 + 3\alpha_3 = 0 α1?+2α2?+3α3?=0。
非齊次線性方程組解的結構
-
若 α 1 , α 2 \alpha_1, \alpha_2 α1?,α2? 均為 A x = b Ax = b Ax=b 的解,則 α 1 ? α 2 \alpha_1 - \alpha_2 α1??α2? 為 A x = 0 Ax = 0 Ax=0 的解。
-
α 0 \alpha_0 α0? 是 A x = b Ax = b Ax=b 的解, η \eta η 是 A x = 0 Ax = 0 Ax=0 的解,則 α 0 + η \alpha_0 + \eta α0?+η 是 A x = b Ax = b Ax=b 的解。
-
A X = b AX = b AX=b 的通解是 A X = b AX = b AX=b 的特解加上 A X = 0 AX = 0 AX=0 的基礎解系的線性組合。
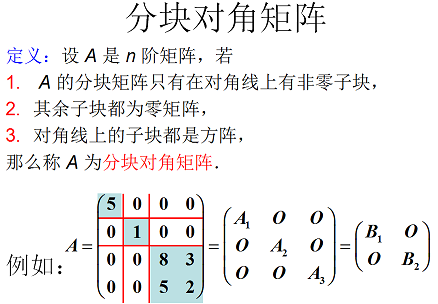
分塊矩陣
-
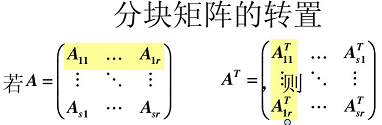
分塊矩陣的轉置:
-
將塊看作元素求矩陣的轉置。
-
每個子塊求轉置。
-
-
分塊矩陣求行列式
H = ( A C 0 B ) H = \begin{pmatrix} A & C \\ 0 & B \\ \end{pmatrix} H=(A0?CB?)
∣ H ∣ = ∣ A ∣ ∣ B ∣ |H| = |A||B| ∣H∣=∣A∣∣B∣
H = ( 0 A B C ) H = \begin{pmatrix} 0 & A \\ B & C \\ \end{pmatrix} H=(0B?AC?)
∣ H ∣ = ( ? 1 ) m n ∣ A ∣ ∣ B ∣ |H| = (-1)^{mn}|A||B| ∣H∣=(?1)mn∣A∣∣B∣(可由 Laplace 定理證明)
-
分塊矩陣求逆矩陣
( A 0 0 B ) ? 1 = ( A ? 1 0 0 B ? 1 ) \begin{pmatrix} A & 0 \\ 0 & B \\ \end{pmatrix}^{-1} = \begin{pmatrix} A^{-1} & 0 \\ 0 & B^{-1} \\ \end{pmatrix} (A0?0B?)?1=(A?10?0B?1?)
( 0 A B 0 ) ? 1 = ( 0 B ? 1 A ? 1 0 ) \begin{pmatrix} 0 & A \\ B & 0 \\ \end{pmatrix}^{-1} = \begin{pmatrix} 0 & B^{-1} \\ A^{-1} & 0 \\ \end{pmatrix} (0B?A0?)?1=(0A?1?B?10?)
實對稱矩陣的對角化
-
α \alpha α 的長度表示為 ∣ ∣ α ∣ ∣ ||\alpha|| ∣∣α∣∣,
( α , α ) = ∣ ∣ α ∣ ∣ 2 (\alpha, \alpha) = ||\alpha||^2 (α,α)=∣∣α∣∣2
-
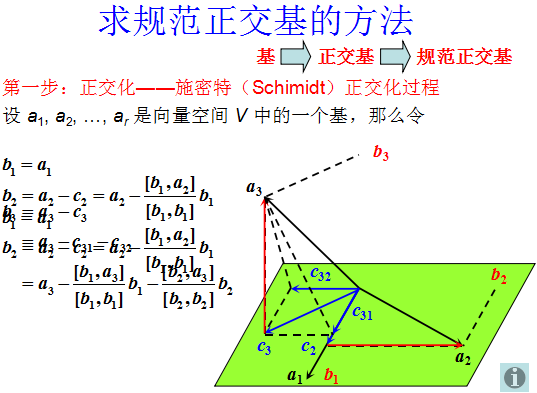
施密特正交化
將一組線性無關的向量組 α 1 , α 2 , … , α r \alpha_1, \alpha_2, \ldots, \alpha_r α1?,α2?,…,αr? 轉化為與之等價的正交向量組 β 1 , β 2 , … , β r \beta_1, \beta_2, \ldots, \beta_r β1?,β2?,…,βr?
β 1 = α 1 \beta_1 = \alpha_1 β1?=α1?
β 2 = α 2 ? ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 \beta_2 = \alpha_2 - \frac{(\alpha_2, \beta_1)}{(\beta_1, \beta_1)}\beta_1 β2?=α2??(β1?,β1?)(α2?,β1?)?β1?
β 3 = α 3 ? ( α 3 , β 1 ) ( β 1 , β 1 ) β 1 ? ( α 3 , β 2 ) ( β 2 , β 2 ) β 2 \beta_3 = \alpha_3 - \frac{(\alpha_3, \beta_1)}{(\beta_1, \beta_1)}\beta_1 - \frac{(\alpha_3, \beta_2)}{(\beta_2, \beta_2)}\beta_2 β3?=α3??(β1?,β1?)(α3?,β1?)?β1??(β2?,β2?)(α3?,β2?)?β2?
β r = α r ? ( α r , β 1 ) ( β 1 , β 1 ) β 1 ? ( α r , β 2 ) ( β 2 , β 2 ) β 2 ? ? ? ( α r , β r ? 1 ) ( β r ? 1 , β r ? 1 ) β r ? 1 \beta_r = \alpha_r - \frac{(\alpha_r, \beta_1)}{(\beta_1, \beta_1)}\beta_1 - \frac{(\alpha_r, \beta_2)}{(\beta_2, \beta_2)}\beta_2 - \cdots - \frac{(\alpha_r, \beta_{r-1})}{(\beta_{r-1}, \beta_{r-1})}\beta_{r-1} βr?=αr??(β1?,β1?)(αr?,β1?)?β1??(β2?,β2?)(αr?,β2?)?β2????(βr?1?,βr?1?)(αr?,βr?1?)?βr?1?
-
實對稱矩陣的相似理論
-
設 A A A 為 n n n 階實對稱矩陣,則存在正交矩陣,使得 P T A P = Λ P^TAP = \Lambda PTAP=Λ( Λ \Lambda Λ 是對角矩陣)。
-
n n n 階方陣相似于對角矩陣的充要條件是由 n n n 個線性無關的特征向量。
-
實對稱矩陣 A A A 的屬于不同特征值的特征向量相互正交。
-
注意事項:
-
奇異矩陣的秩不是滿秩,也叫降秩矩陣, ∣ A ∣ = 0 |A| = 0 ∣A∣=0。非奇異矩陣為滿秩矩陣,行列式不為 0, ∣ A ∣ ≠ 0 |A| \ne 0 ∣A∣=0。
-
矩陣乘法一般不滿足交換律,滿足結合律。
-
初等矩陣定義:單位矩陣經過一次初等變換得到的矩陣(初等矩陣一定可逆)。
-
( A T ) ? 1 = ( A ? 1 ) T (A^T)^{-1} = (A^{-1})^{T} (AT)?1=(A?1)T
-
矩陣左乘行變換,右乘列變換。
-
反對稱矩陣必有 a i j = ? a j i a_{ij} = -a_{ji} aij?=?aji?,所以對角線上的元素都是 0。
-
n n n 階子式的定義:在 m × n m \times n m×n 矩陣 A A A 中,任取 k k k 行與 k k k 列( k ≤ m k \leq m k≤m, k ≤ n k \leq n k≤n),位于這些行列式交叉處的 k 2 k^2 k2 個元素,不改變它們在 A A A 中所處的位置次序而的 k k k 階行列式,稱為矩陣 A A A 的 k k k 階子式。
線性代數知識點整理
cuguanren 于 2022-07-06 15:15:46 發布
前言
為了更好地學習深度學習的相關內容,筆者重新整理了線性代數的主要內容,并以知識點摘要的形式對各部分進行了總結,留待之后進行相關概念的快速復習。
一 行列式
1. 行列式求值
參考 行列式求值(鏈接已沉寂)
2. 七大性質

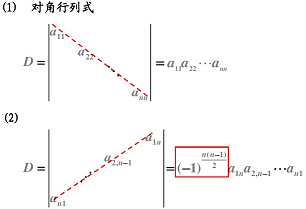
3. 特殊行列式的值

二 矩陣及其運算
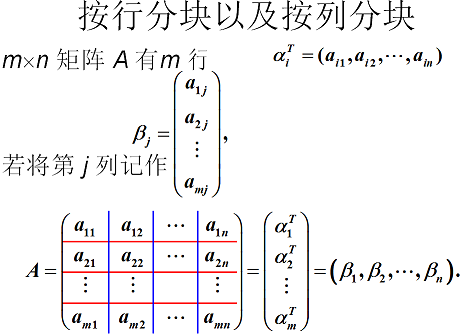
1. 行列向量:
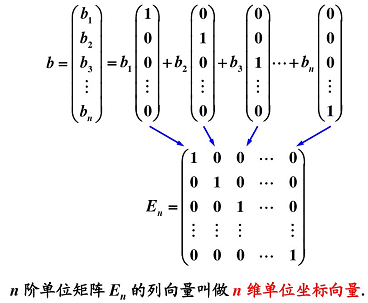
在線性代數中,列向量是一個 n × 1 n \times 1 n×1 的矩陣,即矩陣由一個含有 n n n 個元素的列所組成:列向量的轉置是一個行向量,反之亦然。
2. 可逆矩陣:
矩陣 A A A 為 n n n 階方陣,若存在 n n n 階矩陣 B B B,使得矩陣 A A A、 B B B 的乘積為單位陣,則稱 A A A 為可逆陣, B B B 為 A A A 的逆矩陣。若方陣的逆陣存在,則稱為可逆矩陣或非奇異矩陣,且其逆矩陣唯一。 A A A 是可逆矩陣的充分必要條件是 ∣ A ∣ ≠ 0 |A| \ne 0 ∣A∣=0(方陣 A A A 的行列式不等于 0)。 A A A 的秩等于 n n n( A A A 滿秩)。
3. 常用性質:

4. 伴隨矩陣:

三 矩陣的初等變換和線性方程組
1. 初等變換:
單位矩陣通過三種變換形式得到的矩陣叫做初等矩陣
① 行間或列間互換
② 行或列乘 k k k 倍
③ 某行加上另一行的 k k k 倍(列也如此)


2. 矩陣的秩:定義,特性,求秩
細致內容參考 矩陣的秩,重點強調:可逆矩陣是滿秩矩陣

3. 齊次與非齊次線性方程組
① 兩者區別
齊次線性方程組的常數項全部為零,非齊次方程組的常數項不全為零。
② 表達式不同:
齊次線性方程組表達式: A x = 0 Ax = 0 Ax=0;非齊次方程組常數項不全為零: A x = b Ax = b Ax=b。 A A A 稱為系數矩陣,等號右邊是常數項。
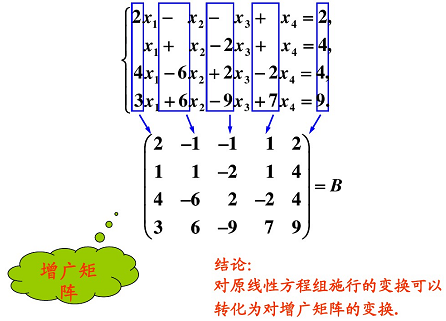
③ 增廣矩陣
又稱 廣置矩陣 ,是在 線性代數中系數矩陣 A A A 的右邊添上線性方程組等號右邊的常數列得到的矩陣,用矩陣( A ∣ B A|B A∣B)表示

④ 兩種方程組的解

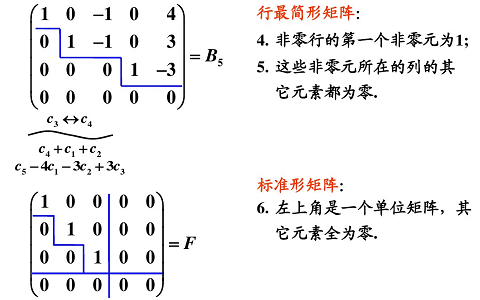
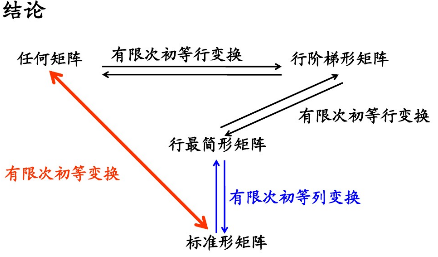
⑤ 最簡行 / 列階梯矩陣:
-
只能行變換。
-
化簡時,從左上角第一個非零元素開始,其下元素需全部化為零,再找階梯下一個元素,其下元素化為零。
-
行階梯接著可化為行最簡,階梯每行左起第一個元素為 1。
-
行變換只能化為行最簡,列一樣。
因此,不能交叉使用兩種變換得到一種最簡矩陣。
4. 等價矩陣:
在線性代數和矩陣論中,有兩個 m × n m \times n m×n 階矩陣 A A A 和 B B B,如果這兩個矩陣滿足 B = Q A P B = QAP B=QAP( P P P 是 n × n n \times n n×n 階可逆矩陣, Q Q Q 是 m × m m \times m m×m 階可逆矩陣),那么這兩個矩陣之間是等價關系。也就是說,存在可逆矩陣( P P P、 Q Q Q),使得 A A A 經過有限次的初等變換得到 B B B。
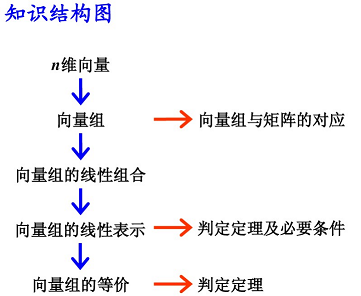
四 向量組的線性相關性
1. 線性表示:
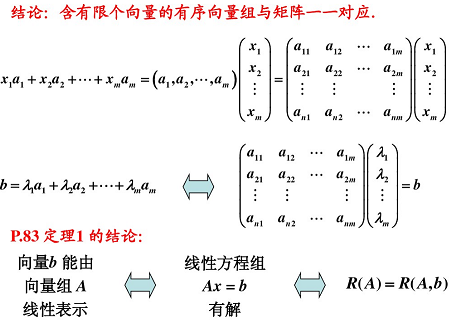
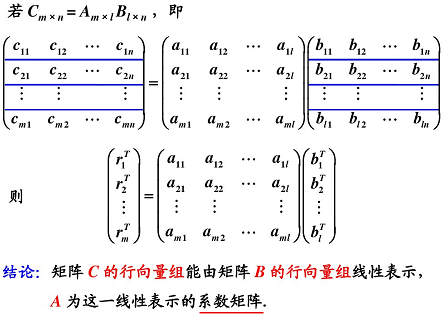
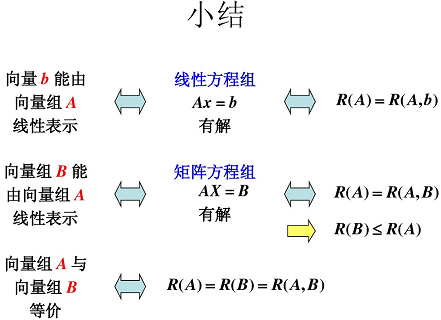
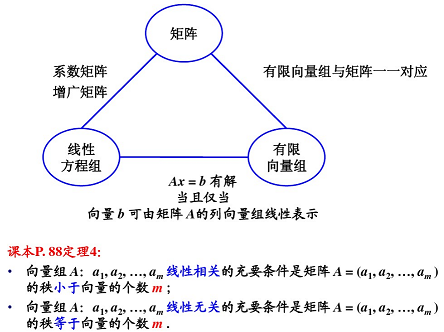
對于兩個向量組:兩個向量組 A A A、 B B B,若 A A A 組中每一個向量都可以由向量組 B B B 線性表示,則稱向量組 A A A 可由向量組 B B B 線性表示。(向量 b b b 能由向量組 X X X 線性表示的充要條件是: R ( A ) = R ( A , B ) R(A) = R(A, B) R(A)=R(A,B))
系數矩陣在左邊時可以認為是對行進行線性變換,在右邊時可以認為對列進行線性變換。
2. 線性相關性判斷:
定義由第一種方法給出, A A A 向量組的構成元素 a i a_i ai? 都是向量
初等行變換不改變列向量的線性相關性,也不改變行向量的線性相關性。

3. 解的情況

五 相似矩陣以及二次型
只有方陣具有特征值與特征向量,不同特征值所對應的特征向量之間線性無關
形象的例子:如果把矩陣看作運動的話,那么
-
特征值就是運動的速度
-
特征向量是運動的方向
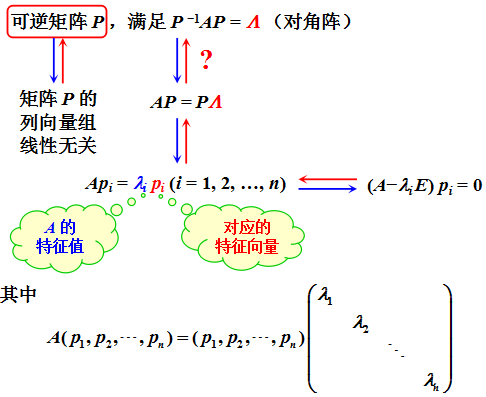
1. 特征值和特征向量的定義
實數 λ \lambda λ 為特征值,向量 p p p 為特征向量

2. 特征值和特征向量的求解

3. 特征值和特征向量的性質

4. 矩陣的相似對角化
存在可逆矩陣 P P P 使得矩陣 A A A 滿足 P ? 1 A P = A P^{-1} A P = A P?1AP=A 的對角矩陣(尖符號),則 A A A 稱為可以相似對角化

5. 特征分解和對角矩陣

6. 二次化標準型
考慮到對于深度學習來說,此部分不太重要,暫時進行了略過,留待后日補充。

線性代數知識點總結,基礎概念和計算整理(手寫版)
李問號 已于 2022-11-08 22:18:59 修改
線性代數中一定必須要掌握的基礎概念和計算的整理,簡單易懂,適合入門和復習。









Ref 2 / 3
-
線性代數 | 知識點整理 Ref 2-CSDN博客
https://blog.csdn.net/u013669912/article/details/147263760 -
線性代數 | 知識點整理 Ref 3-CSDN博客
https://blog.csdn.net/u013669912/article/details/147253667
via:
-
線性代數精要-CSDN博客
https://blog.csdn.net/myarrow/article/details/53365048 -
線性代數知識點整理(自用)-CSDN博客
https://blog.csdn.net/m0_46882548/article/details/108198329 -
線性代數知識點整理_總結-CSDN博客
https://blog.csdn.net/cuguanren/article/details/125640237 -
線性代數知識點總結,基礎概念和計算整理(手寫版)-CSDN博客
https://blog.csdn.net/Bluebro/article/details/127630205




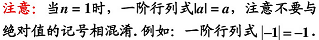
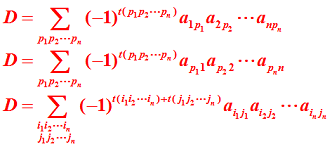
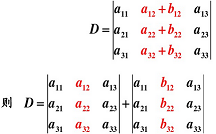
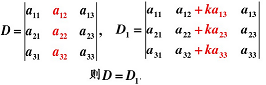












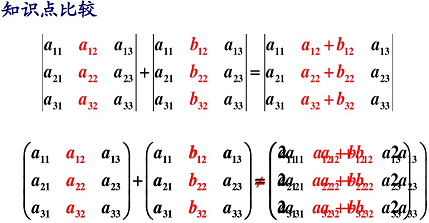




















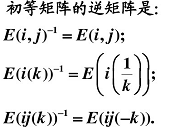






















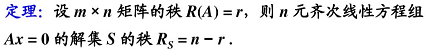













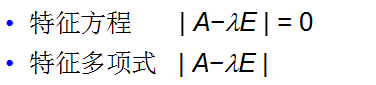









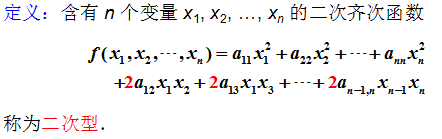







)



)


![[BUG]Cursor C++擴展不支持](http://pic.xiahunao.cn/[BUG]Cursor C++擴展不支持)











:Rust 內存安全基石詳解)