數據結構

前言：這個是針對于藍橋杯競賽常考的數據結構內容，基礎算法比如高精度這些會在下期給大家總結

數據結構

競賽中，時間復雜度不能超過10的7次方（1秒）到10的8次方（2秒）
空間限制：int類型數組總大小不能超過3*10的7次方，二維數組不能超過5000*5000

順序表就是一個數組加上標記數組中有多少元素的數(n)
eg:尾刪就是n--
注意事項：在實行插入和刪除操作時，記得檢查數組中有無位置可以進行

vector容器創建變量常用的方法：<>中的類型可以換
vector<int>a;//搭建一個可變長的數組
vector<int>a;//指定好了一個空間，大小為N
vector<int>a[N];//創建N個vector,vector里存放的是int類型的數據
N個vector用時要eg:a[2].resize(3)

存在迭代器的容器才可以用范圍for去遍歷

程序超時，一般不考慮是容器的問題

鏈表的靜態實現：單鏈表：要頭指針，下一個元素的分配的位置，指針域和數據域  然后下標0位置是哨兵位
注意：在進行操作時，一直讓h為頭指針前提：h是頭指針，id是下一個元素分配的位置，e[n]是數據域，ne[n]是指針域頭插一個數據x：
將x放在e[++id]中 x的右指針指向哨兵位的后繼 哨兵位的右指針指向x所在位置遍歷鏈表：
for(int i = ne[h];i;i = ne[i])按值查找：
1.遍歷鏈表
2.多次查詢并且鏈表中沒有重復數的話，可以用哈希表優化在任意位置之后插入元素：
(在存儲位置p后插入一個元素x)
x放在e[++id]里面，把x位置指向p后面的位置，把p位置指向x刪除任意元素之后的元素：
(刪除存儲位置為p后面的元素)
先判斷p是不是最后一個元素，讓p指向下一個元素的下一個元素雙向鏈表：
比單鏈表加了一個前指針域pre[n]頭插：
x所在位置id左指向哨兵位，右指向哨兵位的下一個位置
之后先修改頭結點的指針，再修改哨兵位的在任意位置之后插入元素：
先讓x的左指針指向p，右指針指向p的后繼
先讓p的后繼的左指針指向id,再讓p的右指針指向id在任意位置之前插入元素：
先讓x的左指針指向p的前驅，右指針指向p
先p的前驅的右指針指向x，再讓p的左指針指向id刪除任意位置(q)的元素：
將q位置的左右指針那兩端縫合在一起就可以了循環列表的話，就是讓單鏈表的最后一個位置的右指針指向頭結點就可以了

棧：只允許在棧頂進行數據插入和刪除
STL中是stack
進棧和出棧時記得檢查空間還有沒有

有時寫一行會好看些
eg：
int b = st.top();st.pop();

隊列：

特性：先進先出

只允許在表尾進行插入操作，在表頭進行刪除操作

樹：
孩子表示法：(用于在無根樹中，即父子關系不明確，因為把與該結點相連的點全部保存下來)
實現方法：
1.用vector數組實現：
假如樹有n個結點的話
創建一個n+1大小的vector數組edge[n+1]
vector<int>edge[n+1];
edge[i]中儲存著i號結點所連接的結點
對于i的孩子，直接edge[i].push_back()進去即可2.用鏈式前向星(其本質是用數組來模擬鏈表)實現
用的是雙向鏈表
鏈式前向星具體怎么實現的自己要知道

樹的遍歷：
1.DFS(深度優先遍歷)：
一條路走到黑    具體流程：
1.從根節點出發，依次遍歷每一棵子樹 2.遍歷子樹的時候,重復第一步
時間復雜度O（N）2.BFS（寬度優先搜索）
一層搜索完了再去下一層搞   具體流程：(借助隊列)：
1.初始化一個隊列 2.根節點入隊，同時標記該節點已經入隊
3.當隊列不為空時，拿出隊頭元素訪問，然后將隊頭元素的孩子入隊，同時打上標記
4.重復3過程，直到隊列為空
這里標記其實是為了跟圖結構那里統一，好記這兩種方式的時間復雜度都是O(N)
像這種有英文簡寫的，在設置自定義函數時，直接寫eg:bfs就很不錯

二叉樹：

分類：滿二叉樹、完全二叉樹等

一般用順序存儲和鏈式存儲

1.順序存儲(一般只用于接近滿的二叉樹或者滿二叉樹)：

其實就是用數組去存儲

規則：針對與結點i來說：

如果父存在，父結點的下標為i/2;

如果左孩子存在，其結點下標為i*2;

如果右孩子存在，其結點下標位為i*2+1；

?

2.鏈式存儲:

也是用數組模擬

創建兩個數組l[N],r[N];

l[i]表示結點i的左孩子，r[i]表示結點i的右孩子

二叉樹的遍歷：
1.DFS:（分為三種）
先序遍歷的順序；根 左 右
中序遍歷的順序：左 根 右
后序遍歷的順序：左 右 根
先中后其實就是看根被插在哪(一直是左右)
eg：自定義命名可以先序遍歷dfs1
自己手動模擬的話：
先序遍歷就是經過一次就行
中序遍歷的話就是經過兩次才那啥
后序遍歷的話就是經過三次2.BFS
跟常規樹的方法差不多，借助隊列

堆：

1.是完全二叉樹

2.要么是大根堆，要么是小根堆

存儲方式的話一般用順序儲存

優先級隊列(即堆)：priority_queue
當優先級隊列中存儲結構體時，要重載<運算符才行
eg：
struct node 
{int a,b,c;
//以b為基準，定義大根堆
bool operator<(const node&x)const
{
return b < x.b;}//以b為基準定義小根堆
bool operator<(const node&x)const
{
return b > x.b;//第一個b是調用<的那個數}
當然，這里只能要一個}
結構體在里面的使用方法
eg:
priority_queue<node>heap;
heap.push({2,3,4})

二叉搜索樹的性質：(BST的性質)

1.左子樹的結點值<根結點<右子樹的結點值

2.左子樹和右子樹也分別是一顆二叉搜索樹

AVL和常規的二叉搜索樹很少用，一般用STL里面的紅黑樹

紅黑樹簡稱BST：其規則：

1.左根右

2.根葉黑（這里的根節點指最上面那一個{一般都是指這個}，葉子結點指的是補為滿二叉樹時的空結點）("最后"的葉子結點下面要補上空節點，這個建議看一下圖)

3.不紅紅

4.黑路同

5.為二叉搜索樹

其的兩個性質：

1.從根結點到葉結點的最長路徑不大于最短路徑的兩倍(理解)

2.有n個結點的紅黑樹，高度h<=2log2(n+1)

排序的話一般都是用的sort 
像插入排序 選擇排序 冒泡排序 堆排序 快速排序 歸并排序這些沒有sort快
sort是綜合了三種排序的

C++中的隨機函數：
#include<ctime>
srand(time(0));//種下一個隨機數種子
b = rand();//會生成一個隨機值給b
c = （b%m+1）+n//獲得的是在[n,m+n]的隨機數

??

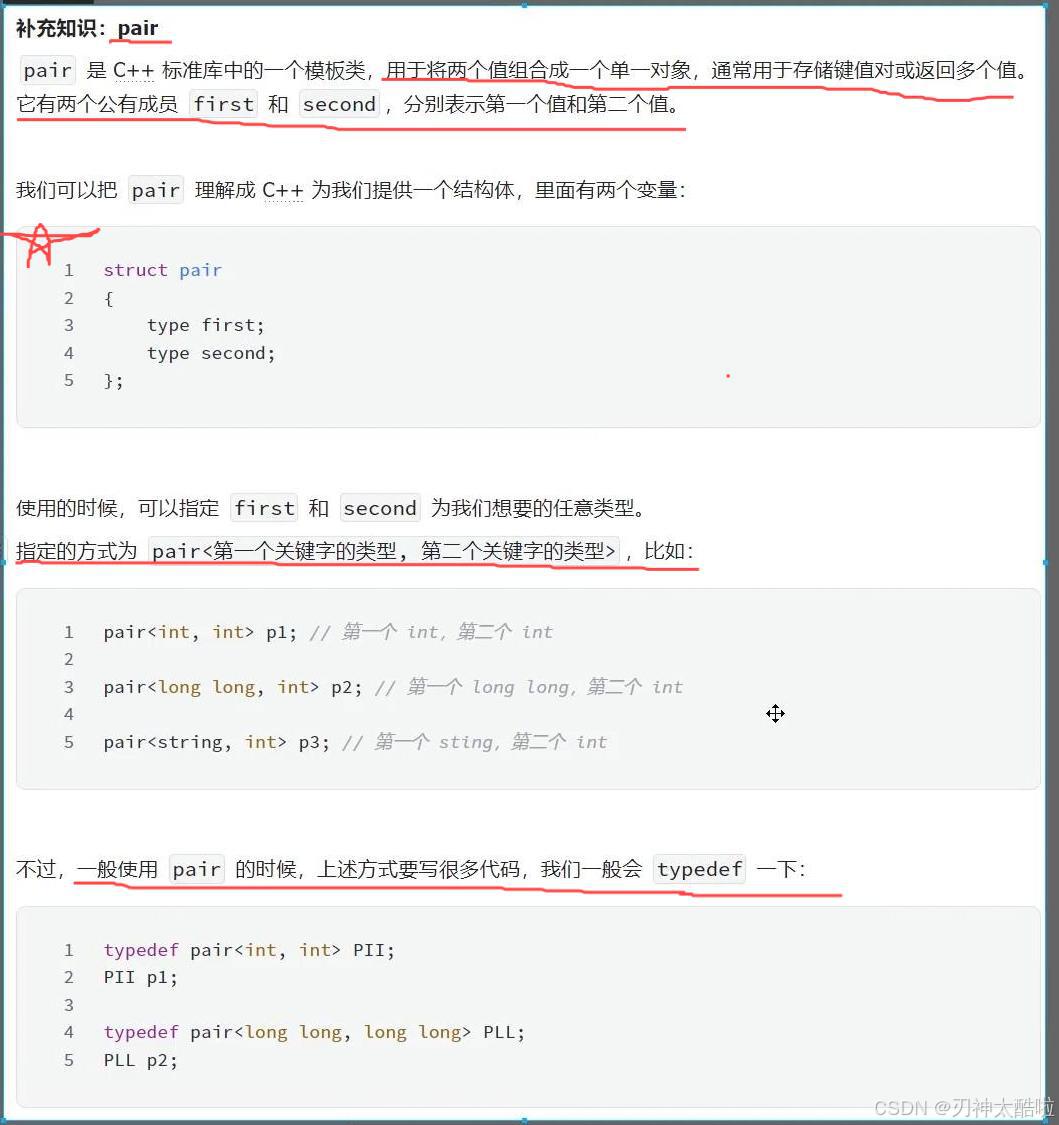pair類型的的重命名方式一般是采用eg:兩個都是int類型的話就是PII,（I為int的首字母的大寫）

vector<int> a[10];  
在C++中聲明了一個數組，這個數組有10個元素，每個元素都是一個 vector<int> 。
每個vector<int>里可以存很多個數，但是要擴容才行
這種數據結構在需要固定數量的動態數組時非常有用
例如，當你有一個固定數量的學生，但每個學生的成績數量不固定時。

常見的算法知識

前面的數據先不驗，從某個相鄰(有多少搞多少)開始才逐個向外驗
這種題通常要用棧
eg:題目：有效的括號(leetcode里面有)、后綴表達式(洛谷里面有)

還原字符串中整數的方法：
eg:ch = '9';t = '9'-'0';

常用bool st[N]來表示i這個元素是否已經在了
用此可以解決快速查找i是不是已經在了或者有無被訪問過
(在第一次錄入時，改成true)

先進先出'數組'問題一般用隊列去解決
eg:海港(洛谷)

處理一個地方不同種人進出時，種類個數:
int cnt[N];//cnt[i]表示這個地方第i個種類的有多少個
int kinds;//統計種類個數
cnt[i]從1變成0時，kinds--;從0變成1時，kinds++；
例題:海港(洛谷)

樹的問題一般都要用到遞歸
堆適合用于每次取出最大或者最小，(再將最大或最小衍生的給放進去)

想把一組數變成堆的話，有兩種方法：
1.用數組存下這組數，然后把數組調整成一個堆
2.創建一個堆，然后將這組數依次插入到堆中

topK問題：
用堆解決
如果是求第k小，就用大根堆
1.維護一個大小為k的大根堆
2.對于每次來的元素，先進堆，再刪除堆頂元素，此時堆頂元素就是第k小(每個元素都要放進來過)
如果是求第k大，就用小根堆，...

像這種可以用單調性簡化問題的題的做法：
1.先存認為小的數(怎么寫方便怎么來，就算跟后面的比又不是特別小了)
2.堆中一般還要存關系量(3要用)
3.將堆頂彈出后，搞入與堆頂關系量相近的

有時要設置左右護法，防止越界訪問
eg:做++--時  特別是紅黑樹那里找小于等于x的最大值

模加模：
解決取模之后的模變成負數的問題(讓他變為正數):
(key%N+N)%N

哈希表常用來解決一個東西有沒有重復出現或者重復出現了幾次的問題

算法題中的經典操作:用空間代替時間

模擬得到浮點數的小數部分p
double d = 6.5;
int q = (int)d;
double p = d - q;小數四舍五入成整數的方法
假設a是四舍五入之后的，b是四舍五入之前的
有a = (int)(b+0.5);

?

數據結構這里常用的頭文件和容器以及其接口

這個點的話是C++比C語言在解題時優越的地方，可以用容器來省略很多過程
而且使用容器的話，一般比賽是不會無聊到用容器去卡你的時間，也就是說，如果超時了，大概率不是容器的問題

#include<vector>
size-返回實際元素個數
empty-返回順序表是否為空，空則返回true，非空則返回false
begin-返回起始位置的迭代器
end-返回終點位置的下一個位置的迭代器
push_back-尾部插入一個元素
pop_back-尾部刪除一個元素
front-返回首元素
back-返回尾元素
resize-修改vector的大小
clear-清空vector(把大小搞為1)

stack容器（棧）
頭文件：#include<stack>
創建:stack<T>st;//st是變量名，可以改；T是任意類型的數據
size empty 
push:進棧
pop:出棧
top:返回棧頂元素，但是不會刪除棧頂元素

queue(隊列)：
頭文件:#include<queue>
創建:queue<T>q;//q是變量名，T是任意類型的數據
size empty push pop
front:返回隊頭元素，但不會刪除
back:返回隊尾元素，但不會刪除
不可以用clear來直接清除隊列

deque(雙端隊列):
頭文件#include<deque>
創建-和queue方式一樣
size empty front back
push_front－頭插
push_back－尾插
pop_front－頭刪
pop_back－尾刪
clear－清除隊列

priority_queue(優先級隊列)
頭文件：#include<queue>
size empty 
push－往優先級隊列里面添加一個元素(自動排序了)
pop－刪除優先級最高的元素(也會自動排序)
top－獲取優先級最高的元素
創建:
priority_queue<數據類型,存數據的結構，數據之間的比較方式>
存數據的結構沒寫時，默認是vector
數據之間比較方式沒寫時，默認是大根堆
如果想改成小根堆，數據之間的比較方式這里就要寫greater<數據類型>

紅黑樹：
set和multiset的區別:set不能存相同元素，multiset可以存相同元素
(其余使用方式完全一致)，下面以set舉例
頭文件:#include<set>//multiset也為此
創建：set<T>q//T為任意數據類型，q為變量名
size empty begin end
可以用范圍for遍歷整個紅黑樹(遍歷是按照中序遍歷的順序，因此是有序的序列)
insert:向紅黑樹中插入一個元素(時間復雜度logN)
erase:刪除一個元素(時間復雜度:logN)
find:查找一個元素，返回的是迭代器(時間復雜度:logN)
count：查詢元素出現的次數，一般用來判斷元素是否在紅黑樹中(時間復雜度:logN)
如果想查找元素是否在set中，我們一般使用count（count不是返回的迭代器）
lower_bound(x):大于等于x的最小元素，返回的是迭代器(時間復雜度：logN)
upper_bound(x):大于x的最小元素，返回的是迭代器(時間復雜度：logN)
如果嘗試向 set 中插入相同的元素， set 會忽略后續的插入操作，因為 set 中已經存在該元素。

紅黑樹：
map和multimap的區別：map不能存相同元素，multimap可以，其余使用方法一樣
和set的區別：set里面存的一個關鍵字，map里面是一個關鍵字key 一個與關鍵字綁定的值value
頭文件:#include<map>//multimap也為此
創建：map<key,value>mp1
eg：map<int,vector<int>>mp2;
size empty begin end erase find count lower_bound upper_bound//跟set使用方法差不多
用范圍for遍歷時，也為中序遍歷，得到有序的序列
insert:向紅黑樹中插入一個pair類型的，要用{}形式
eg:mp.insert({1,2})
此外map 和multimap重載了[],使其能夠像數組一樣使用
eg:mp[2]=......//...這里的值是value的
但是注意：如果用[]插入的時候，[]里面的內容不存在于map里，會先插入，然后再拿值
插入的時候，第一個關鍵字就是[]里面的內容，第二個關鍵字是一個默認值
所以一般要eg:
if(mp.count('趙六')&&mp['趙六']==4)....如果單單后面那個，就會插入一個趙六了
找小于等于x的最大值的話要lower_bound的迭代器--即可

哈希表：
unordered_set 和unordered_multiset
和set的區別：set有序，unordered_set無序
頭文件:#include<unordered_set>//unordered_multiset也為此
創建：unordered_set<T>q;
size empty begin end insert erase find count
也可以用范圍for遍歷，但是遍歷出來的結果是無序的

哈希表:
unordered_map和unordered_multimap
和map的區別以及和map的共同點都和上面一樣
除了范圍for遍歷出來是無序的以外，其他都和map的接口用途一樣

查詢庫函數和容器用法的網站

查詢具體用法：https://legacy.cplusplus.com/reference/
如果對用法還是不會的話，可以點擊這個鏈接去查詢具體用法