---

前言

webrtc中的高通濾波器可以大幅抑制 100 Hz 以下的頻率成分（如 50 Hz 電源噪聲、低頻雜音等），其核心使用一個二階IIR高通濾波器過濾低頻分量。

本篇文章中，將先對于HighPassFilter的創建和使用配置以及整體的使用流程做一個梳理，然后再深入介紹算法實現，并且會使用matlab畫出對應的通帶、阻帶、以及過渡帶方便直觀理解。

|版本聲明：山河君，未經博主允許，禁止轉載

---

一、導讀

在 WebRTC 的語音處理鏈路中，高通濾波器（High Pass Filter，HPF）幾乎是必備的一環。它的作用很直接：削弱 100Hz 以下的低頻成分，比如電源嗡聲、桌面震動、風扇噪聲等，從而保證后續 AGC、NS、AEC 模塊處理的信號更干凈。

• 觸發方式：
  可以手動配置開啟，也可能因為啟用 AEC 等模塊而被自動啟用。
• 算法原理：
  HPF 基于二階 IIR 濾波器實現，每個通道/子帶獨立濾波。核心公式：
  $$y[n]=b_{0}x[n]+b_{1}x[n?1]+b_{2}x[n?2]?a_{1}y[n?1]?a_{2}y[n?2]$$
• 濾波器系數：
  根據采樣率（16k/32k/48k）選擇不同的 Butterworth 濾波器參數，保證截止頻率在 ~100Hz。
• 實現特點：
  • 使用 CascadedBiQuadFilter 串聯二階濾波器
  • 支持全頻帶或子帶處理
  • 性能開銷低，適合實時語音處理

二、高通濾波過程

1.HighPassFilter的創建

1）HighPassFilter的作用

HighPassFilter是用于去除音頻輸入中的低頻噪聲（如風聲、風扇、桌面震動等）。例如：在會議中，麥克風經常會錄到桌子震動的‘嗡嗡聲’，WebRTC 的高通濾波器就是專門干掉這種低頻噪聲的。

這個配置常用于語音增強處理鏈（如 AGC、NS、AEC）之前。

2）開啟條件

在 WebRTC 中，主動使用配置項 config.high_pass_filter.enabled = true 可以開啟高通濾波器（High Pass Filter，HPF）。但如果不主動配置，同樣有可能會默認打開高通濾波，如下代碼：

void AudioProcessingImpl::InitializeHighPassFilter(bool forced_reset) {bool high_pass_filter_needed_by_aec =config_.echo_canceller.enabled &&config_.echo_canceller.enforce_high_pass_filtering &&!config_.echo_canceller.mobile_mode;if (submodule_states_.HighPassFilteringRequired() ||high_pass_filter_needed_by_aec) {bool use_full_band = config_.high_pass_filter.apply_in_full_band &&!constants_.enforce_split_band_hpf;int rate = use_full_band ? proc_fullband_sample_rate_hz(): proc_split_sample_rate_hz();size_t num_channels =use_full_band ? num_output_channels() : num_proc_channels();if (!submodules_.high_pass_filter ||rate != submodules_.high_pass_filter->sample_rate_hz() ||forced_reset ||num_channels != submodules_.high_pass_filter->num_channels()) {submodules_.high_pass_filter.reset(new HighPassFilter(rate, num_channels));}} else {submodules_.high_pass_filter.reset();}
}

例如在開啟AEC時，會默認打開高通濾波，這只會影響高通濾波在3A處理時的順序。

3）開啟配置

HighPassFilter創建時受到采樣率和通道數的影響，具體代碼如下：

HighPassFilter::HighPassFilter(int sample_rate_hz, size_t num_channels): sample_rate_hz_(sample_rate_hz) {filters_.resize(num_channels);const auto& coefficients = ChooseCoefficients(sample_rate_hz_);for (size_t k = 0; k < filters_.size(); ++k) {filters_[k].reset(new CascadedBiQuadFilter(coefficients, kNumberOfHighPassBiQuads));}
}

• ChooseCoefficients(sample_rate_hz_)：根據采樣率確定濾波器系數
• new CascadedBiQuadFilter：根據通道數確定創建濾波器個數，同時濾波器獲得系數

在本文中，將以采樣率為16k，單通道為例進行介紹

2.高通濾波整體過程

1）觸發時機

上文中已經說過，在不同條件下創建的HighPassFilter將會在不同時機進行高通濾波，以在處理近端采集信號做增益之前觸發高通濾波舉例：

if (submodules_.high_pass_filter &&(!config_.high_pass_filter.apply_in_full_band ||constants_.enforce_split_band_hpf)) {submodules_.high_pass_filter->Process(capture_buffer,/*use_split_band_data=*/true);}

其中滿足以下兩個條件時會進行高通濾波器

• submodules_.high_pass_filter 不為空（即高通濾波器模塊已經初始化）
• 滿足以下任意一個：
  • !config_.high_pass_filter.apply_in_full_band ：表示不在 full-band 上應用 HPF
  • constants_.enforce_split_band_hpf 為真：強制在 split-band 上應用 HPF。

對于條件二，是判斷是否進行了頻帶分割對于全頻帶或者各個子頻道分別做高通濾波，而默認是對于各個子帶做高通濾波的

2）濾波器創建

HPF濾波器真正創建構造函數有兩種方式：

CascadedBiQuadFilter::CascadedBiQuadFilter(const CascadedBiQuadFilter::BiQuadCoefficients& coefficients,size_t num_biquads): biquads_(num_biquads, BiQuad(coefficients)) {}CascadedBiQuadFilter::CascadedBiQuadFilter(const std::vector<CascadedBiQuadFilter::BiQuadParam>& biquad_params) {for (const auto& param : biquad_params) {biquads_.push_back(BiQuad(param));}
}

前者是根據給定濾波器系數創建，后者是根據給定零極點計算出濾波器系數，具體的參數下文中會詳細介紹。

3）高通濾波過程

在webrtc之子帶分割下——SplittingFilter源碼分析文章中，對于頻帶分割規則有過詳細介紹：

• 對于32k采樣率應該劃分為兩個子帶
• 對于48k采樣率應該分為三個自帶
• 對于16k采樣率不劃分子帶

而在使用HPF過程中，會默認對于每個通道的每個子帶進行高通濾波，如以下代碼

void HighPassFilter::Process(AudioBuffer* audio, bool use_split_band_data) {RTC_DCHECK(audio);RTC_DCHECK_EQ(filters_.size(), audio->num_channels());if (use_split_band_data) {for (size_t k = 0; k < audio->num_channels(); ++k) {rtc::ArrayView<float> channel_data = rtc::ArrayView<float>(audio->split_bands(k)[0], audio->num_frames_per_band());filters_[k]->Process(channel_data);}} else {for (size_t k = 0; k < audio->num_channels(); ++k) {rtc::ArrayView<float> channel_data =rtc::ArrayView<float>(&audio->channels()[k][0], audio->num_frames());filters_[k]->Process(channel_data);}}
}

而對于16k，單通道的音頻信號，只需要進行一次濾波即可，具體的算法進行下文會詳細介紹。

三、算法實現

1.原理

1）濾波器種類

CascadedBiQuadFilter是一種二階的IIR濾波器，并且會根據創建時的參數來指定是否進行串聯，如下文參數中：

• 根據給定濾波器系數創建：num_biquads參數指定串聯個數
• 根據給定零極點計算創建：std::vector<CascadedBiQuadFilter::BiQuadParam>個數決定串聯個數

在本文中，創建時傳入的是給定的濾波器系數，并且指定濾波器個數為：

constexpr size_t kNumberOfHighPassBiQuads = 1;

根據二階IIR濾波器差分方程，見文章語音信號處理六——遞歸/非遞歸離散時間系統與差分方程：
$$y[n]=b_{0}x[n]+b_{1}x[n?1]+b_{2}x[n?2]?a_{1}y[n?1]?a_{2}y[n?2]$$
而結構體BiQuadCoefficients 保存濾波器系數

struct BiQuadCoefficients {float b[3];float a[2];};

2）給定系數創建濾波器

根據采樣率確定：

const CascadedBiQuadFilter::BiQuadCoefficients& ChooseCoefficients(int sample_rate_hz) {switch (sample_rate_hz) {case 16000:return kHighPassFilterCoefficients16kHz;case 32000:return kHighPassFilterCoefficients32kHz;case 48000:return kHighPassFilterCoefficients48kHz;default:RTC_NOTREACHED();}RTC_NOTREACHED();return kHighPassFilterCoefficients16kHz;
}

其中根據奎納斯采樣定理：

• 16k采樣率過濾保留：100Hz~8kHz頻率分量
• 32k采樣率過濾保留：100Hz~16kHz頻率分量
• 48k采樣率過濾保留：100Hz~24kHz頻率分量

濾波器系數如下：

// [B,A] = butter(2,100/8000,'high')
constexpr CascadedBiQuadFilter::BiQuadCoefficientskHighPassFilterCoefficients16kHz = {{0.97261f, -1.94523f, 0.97261f},{-1.94448f, 0.94598f}};// [B,A] = butter(2,100/16000,'high')
constexpr CascadedBiQuadFilter::BiQuadCoefficientskHighPassFilterCoefficients32kHz = {{0.98621f, -1.97242f, 0.98621f},{-1.97223f, 0.97261f}};// [B,A] = butter(2,100/24000,'high')
constexpr CascadedBiQuadFilter::BiQuadCoefficientskHighPassFilterCoefficients48kHz = {{0.99079f, -1.98157f, 0.99079f},{-1.98149f, 0.98166f}};

3）給定零極點創建濾波器

值得注意的是，創建高通濾波器時不會使用到這種方式。

根據二階IIR濾波器傳遞函數，見文章語音信號處理十三——Z變換二（有理z變換、穩定性與反變換）：
$$H(z)=\frac{b_0+b_1{z}^{?1}+b_2{z}^{?2}}{1+a_0{z}^{?1}+a_1{z}^{?2}}$$
而對于代碼中

CascadedBiQuadFilter::BiQuad::BiQuad(const CascadedBiQuadFilter::BiQuadParam& param): x(), y() {float z_r = std::real(param.zero);float z_i = std::imag(param.zero);float p_r = std::real(param.pole);float p_i = std::imag(param.pole);float gain = param.gain;if (param.mirror_zero_along_i_axis) {// Assuming zeroes at z_r and -z_r.RTC_DCHECK(z_i == 0.f);coefficients.b[0] = gain * 1.f;coefficients.b[1] = 0.f;coefficients.b[2] = gain * -(z_r * z_r);} else {// Assuming zeros at (z_r + z_i*i) and (z_r - z_i*i).coefficients.b[0] = gain * 1.f;coefficients.b[1] = gain * -2.f * z_r;coefficients.b[2] = gain * (z_r * z_r + z_i * z_i);}// Assuming poles at (p_r + p_i*i) and (p_r - p_i*i).coefficients.a[0] = -2.f * p_r;coefficients.a[1] = p_r * p_r + p_i * p_i;
}

其中：

• z_r ,z_i：是零點位置
• p_r ,p_i ：是極點位置
• gain ,p_i ：是極點位置
• mirror_zero_along_i_axis：是否沿虛軸鏡像零點（實數對稱）

零點位置

• 零點沿虛軸鏡像（$z$與$?z$），其傳遞函數分子為：
  $$(1?z_r{z}^{?1})(1+z_r{z}^{?1})=1?z_r^2{z}^{?2}$$
  那么對應系數為：

b[0] = gain * 1.f;
b[1] = 0.f;
b[2] = gain * -(z_r * z_r);

• 常規復共軛零點（$z=z_r\pm z_{i}i$），其傳遞函數分母為：
  $$(1?(z_r+j{z}_i)z^{?1})(1+(z_r?j{z}_i)z^{?1})=1?2z_r^2{z}^{?1}+(z_r^2+z_i^2)z^{?1}$$
  那么對應的系數為

else {coefficients.b[0] = gain * 1.f;coefficients.b[1] = gain * -2.f * z_r;coefficients.b[2] = gain * (z_r * z_r + z_i * z_i);
}

極點位置

極點部分$(p_r\pm p_i?i)$為復共軛，直接用共軛復數對展開，其傳遞函數分母為：
$$1?2p_r{z}^{?1}+(p_r^2+p_i^2)z^{?2}$$

  coefficients.a[0] = -2.f * p_r;coefficients.a[1] = p_r * p_r + p_i * p_i;

2.matlab分析

對于給定濾波器系數，使用matlab畫出幅頻響應如下圖：

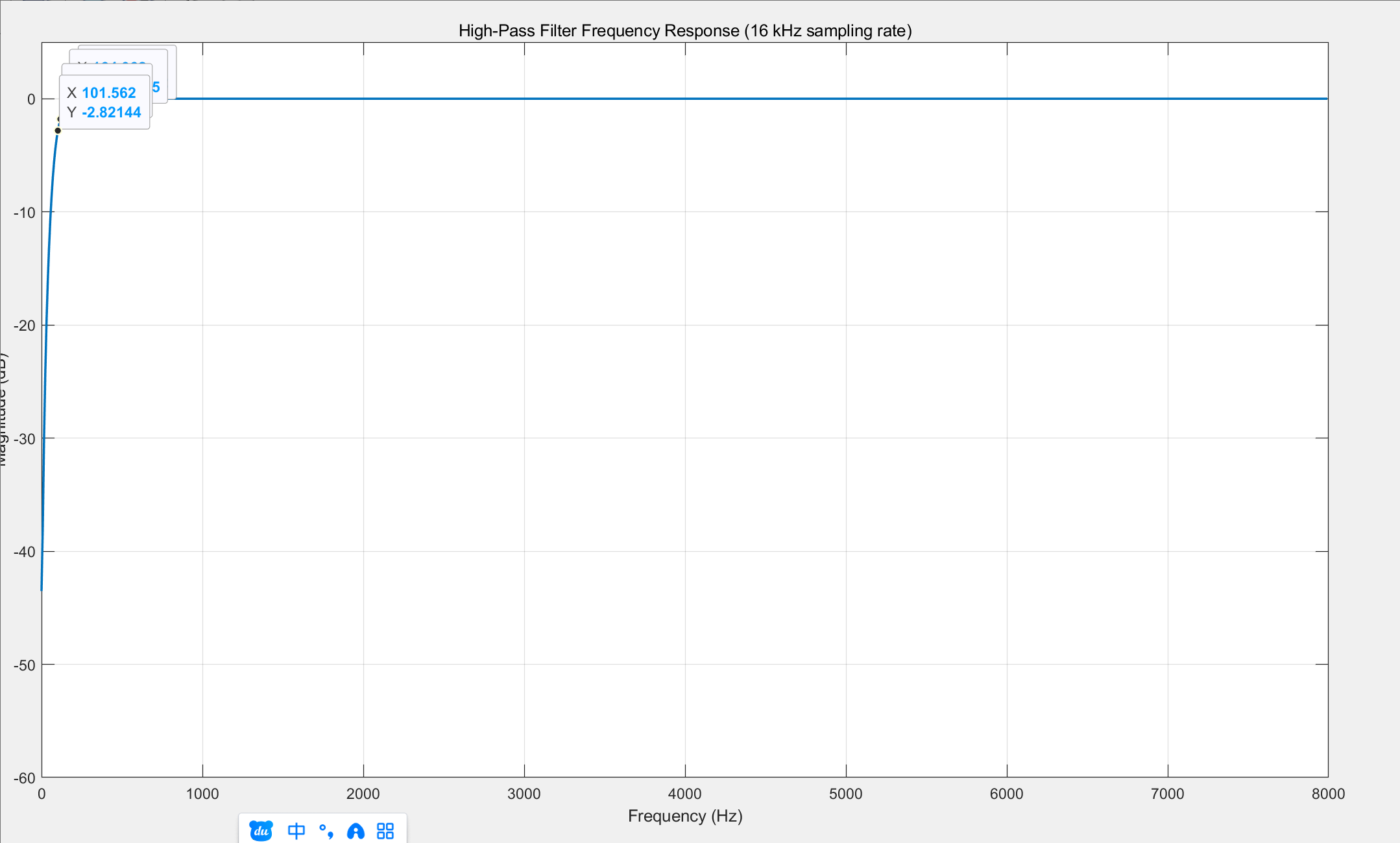
對應代碼如下

% 二階濾波器系數
b = [0.97261, -1.94523, 0.97261];     % 分子系數（zeros）
a = [1.0, -1.94448, 0.94598];         % 分母系數（poles）% 使用 freqz 繪制頻率響應（默認 512 點）
fs = 16000; % 采樣率
[H, f] = freqz(b, a, 1024, fs);% 繪制幅頻響應
figure;
plot(f, 20*log10(abs(H)), 'LineWidth', 1.5);
grid on;
xlabel('Frequency (Hz)');
ylabel('Magnitude (dB)');
title('High-Pass Filter Frequency Response (16 kHz sampling rate)');
ylim([-60 5]);

3.濾波過程

1）串聯二級IIR濾波器

在進行濾波時，會對于每個IIR濾波器進行串聯計算

void CascadedBiQuadFilter::Process(rtc::ArrayView<float> y) {for (auto& biquad : biquads_) {ApplyBiQuad(y, y, &biquad);}
}

2）濾波計算

濾波計算實際就是根據給定的濾波器系數進行反饋回路計算，即：
$$y[n]=b_{0}x[n]+b_{1}x[n?1]+b_{2}x[n?2]?a_{1}y[n?1]?a_{2}y[n?2]$$
代碼如下：

void CascadedBiQuadFilter::ApplyBiQuad(rtc::ArrayView<const float> x,rtc::ArrayView<float> y,CascadedBiQuadFilter::BiQuad* biquad) {RTC_DCHECK_EQ(x.size(), y.size());const auto* c_b = biquad->coefficients.b;const auto* c_a = biquad->coefficients.a;auto* m_x = biquad->x;auto* m_y = biquad->y;for (size_t k = 0; k < x.size(); ++k) {const float tmp = x[k];y[k] = c_b[0] * tmp + c_b[1] * m_x[0] + c_b[2] * m_x[1] - c_a[0] * m_y[0] -c_a[1] * m_y[1];m_x[1] = m_x[0];m_x[0] = tmp;m_y[1] = m_y[0];m_y[0] = y[k];}

這段算法整體過程如下：

每個樣本：x[n] ─┬─? b0 ──┬────┐├─? b1 ─┼────┼──? y[n] = 輸出├─? b2 ─┘    ▼└─ y[n-1] ─ a0 ──┐y[n-2] ─ a1 ─┘

而結構體BiQuad中會保存反饋回路中的輸入輸出反饋x[2]，y[2]

struct BiQuad {explicit BiQuad(const BiQuadCoefficients& coefficients): coefficients(coefficients), x(), y() {}explicit BiQuad(const CascadedBiQuadFilter::BiQuadParam& param);void Reset();BiQuadCoefficients coefficients;float x[2];float y[2];};

---

總結

webrtc中的高通濾波器是基于二階IIR濾波器進行設計的，但是對于二階IIR濾波器不僅僅會在高通濾波器中應用，在以后的webrtc算法介紹中CascadedBiQuadFilter將還會出現。

反正收藏也不會看，不如點個贊吧！