給你一個大小為?n x n?的整數方陣?grid。返回一個經過如下調整的矩陣:
- 左下角三角形(包括中間對角線)的對角線按?非遞增順序?排序。
- 右上角三角形?的對角線按?非遞減順序?排序。
示例 1:
輸入:?grid = [[1,7,3],[9,8,2],[4,5,6]]
輸出:?[[8,2,3],[9,6,7],[4,5,1]]
解釋:
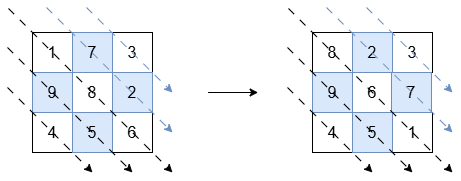
標有黑色箭頭的對角線(左下角三角形)應按非遞增順序排序:
[1, 8, 6]?變為?[8, 6, 1]。[9, 5]?和?[4]?保持不變。
標有藍色箭頭的對角線(右上角三角形)應按非遞減順序排序:
[7, 2]?變為?[2, 7]。[3]?保持不變。
示例 2:
輸入:?grid = [[0,1],[1,2]]
輸出:?[[2,1],[1,0]]
解釋:

標有黑色箭頭的對角線必須按非遞增順序排序,因此?[0, 2]?變為?[2, 0]。其他對角線已經符合要求。
示例 3:
輸入:?grid = [[1]]
輸出:?[[1]]
解釋:
只有一個元素的對角線已經符合要求,因此無需修改。
提示:
grid.length == grid[i].length == n1 <= n <= 10-10^5 <= grid[i][j] <= 10^5
分析:由于矩陣的規模很小,可以直接模擬。用一個數組存儲對角線的元素并按照右上對角線非遞減順序,左下角對角線非遞增排序,排好序后再存回原數組即可。
/*** Return an array of arrays of size *returnSize.* The sizes of the arrays are returned as *returnColumnSizes array.* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().*/
int cmp_1(const void *a,const void *b)
{return *(int*)a-*(int*)b;
}
int cmp_2(const void *a,const void *b)
{return *(int*)b-*(int*)a;
}
int** sortMatrix(int** grid, int gridSize, int* gridColSize, int* returnSize, int** returnColumnSizes) {int n=gridSize;*returnSize=n;*returnColumnSizes=(int*)malloc(sizeof(int)*n);for(int i=0;i<n;++i)(*returnColumnSizes)[i]=n;for(int i=0;i<n;++i){int temp_1[n-i+5],temp_2[n-i+5];for(int j=0,k=i;j<n-i;++j,++k)temp_2[j]=grid[k][j],temp_1[j]=grid[j][k];qsort(temp_2,n-i,sizeof(int),cmp_2);qsort(temp_1,n-i,sizeof(int),cmp_1);for(int j=0,k=i;j<n-i;++j,++k)grid[j][k]=temp_1[j],grid[k][j]=temp_2[j];}return grid;
}
)





:H264中的SEI)











