一、實驗概述
????????本實驗旨在利用機器學習技術,基于加州房價數據集(California Housing Dataset)構建一個房價預測模型。實驗涵蓋了從數據加載、探索性數據分析(EDA)、數據預處理到模型構建與評估的完整流程。核心任務是利用房屋的各項特征(如收入中位數、房齡、平均房間數等)來預測房價中位數(MEDV)。
二、數據來源
? ? ? ? 數據集為機器學習經典數據集:加州房價預測,可以從?sklearn.datasets?直接使用?fetch_california_housing?函數加載。
三、實驗過程
1.相關庫與初始數據加載
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.linear_model import Ridge
from sklearn.linear_model import ElasticNet
from sklearn.model_selection import GridSearchCV# 加載數據集
california = fetch_california_housing()
data = pd.DataFrame(california.data, columns=california.feature_names)
data['MEDV'] = california.target # X = data.drop('MEDV', axis=1)
y = data['MEDV']
2.數據探索 (EDA)
????????本實驗通過簡單的統計和可視化對數據進行了初步探索:繪制了特征 (data) 和目標變量 (target) 的分布直方圖與特征之間的相關性熱力圖,并對缺失值進行檢測。
#(2)數據探索
#數據缺失值檢測
df_X = pd.DataFrame(X, columns=feature_names)
df_y = pd.DataFrame(y, columns=["Target"])
print(df_X.isnull().sum())
print(df_y.isnull().sum())#數據異常值檢測
for col in df_X.columns:plt.figure(figsize=(6, 4))sns.boxplot(x=df_X[col])plt.title(f'Boxplot of {col}')plt.show() #特征的基本統計信息
#print(cleaned_df_X.describe())
cleaned_df_X = pd.DataFrame(cleaned_df_X, columns=feature_names) # 將 ndarray 轉換為 DataFrame
cleaned_df_y = pd.DataFrame(cleaned_df_y, columns=["Target"])
cleaned_data = pd.concat([cleaned_df_X, cleaned_df_y], axis=1)# 合并特征和目標變量
corr_matrix = cleaned_data.corr()# 計算相關性矩陣
plt.figure(figsize=(10, 8))
sns.heatmap(corr_matrix,annot=True, # 顯示數值
)
plt.title("特征與目標變量的相關性熱力圖")
plt.show()
?輸出結果如下:
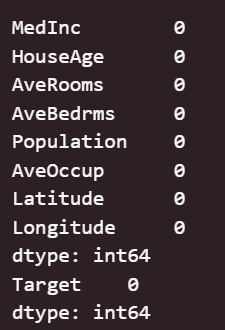
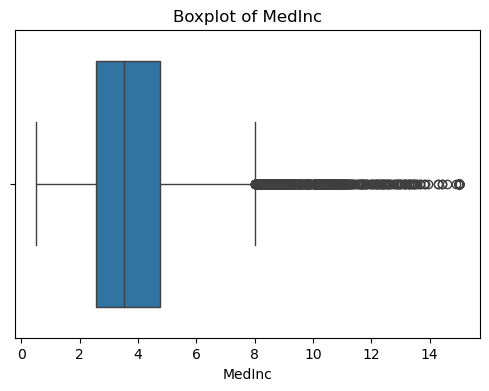
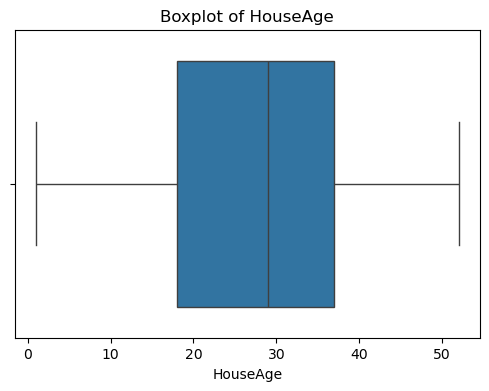
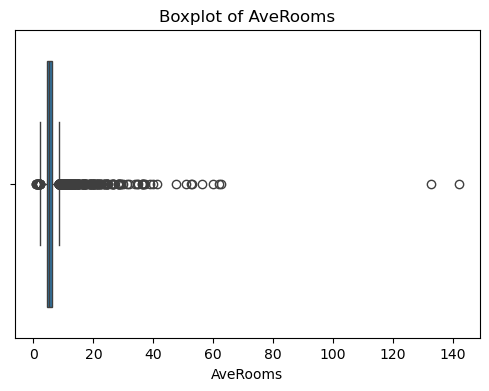
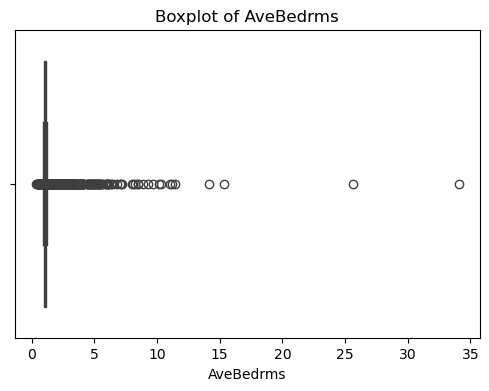
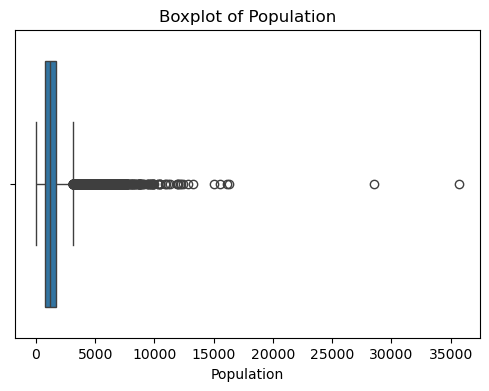
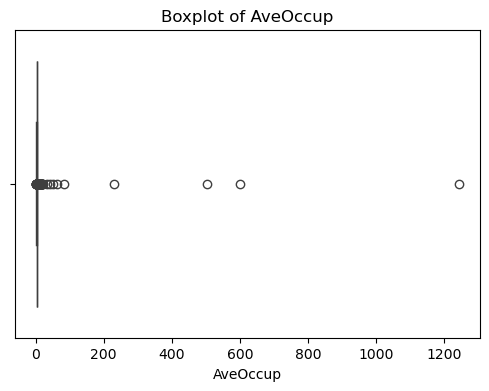
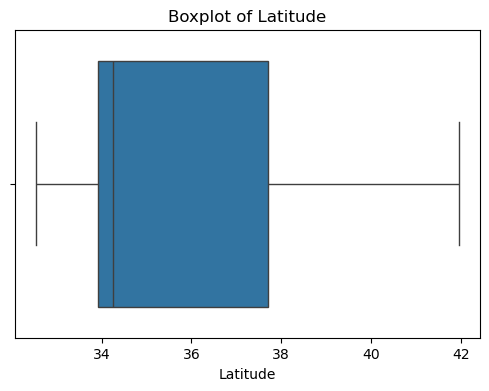
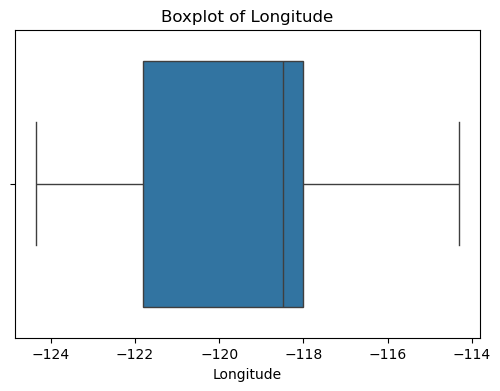
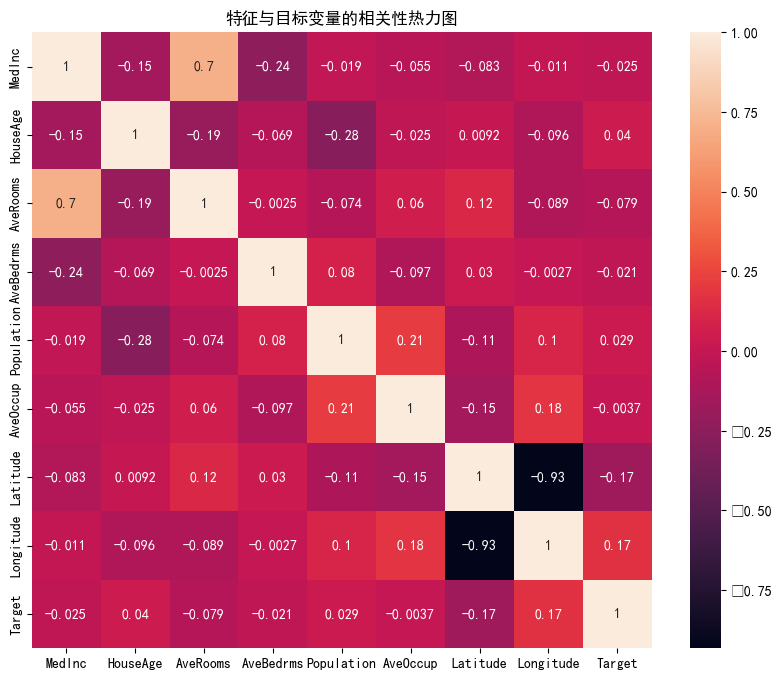
????????可以看出,原始數據無缺失值,部分變量異常值樣本數量較多,后續需要進行基于Z-score方法的異常值處理。由熱力圖可知,部分變量的相關性十分明顯,如變量 Latitude 與變量 Longitude 具有強負相關性,變量AvgRooms 與變量 Medlnc 具有強正相關性。故擬合模型應采用具有正則化的模型進行。
3. 數據預處理
? ? ? ? 主要進行異常值處理、標準化數據、測試訓練集的劃分的任務。
#(3)數據清洗
z_scores_X = stats.zscore(df_X)
z_scores_y = stats.zscore(df_y)
abs_z_scores_X = np.abs(z_scores_X)
abs_z_scores_y = np.abs(z_scores_y) #處理異常值
def remove_outliers_iqr(df, factor=1.5):df_cleaned = df.copy()for col in df.columns:Q1 = df[col].quantile(0.25)Q3 = df[col].quantile(0.75)IQR = Q3 - Q1lower_bound = Q1 - factor * IQRupper_bound = Q3 + factor * IQRdf_cleaned = df_cleaned[(df_cleaned[col] >= lower_bound) & (df_cleaned[col] <= upper_bound)]return df_cleanedcleaned_df_X = remove_outliers_iqr(df_X)
cleaned_df_y = y[cleaned_df_X.index]
print("原始樣本數量:", len(df_X))
print("清洗后樣本數量:", len(cleaned_df_X))# 標準化 X
scaler = StandardScaler()
X_scaled = scaler.fit_transform(cleaned_df_X)
y_scaled = cleaned_df_y# 按照 80% 訓練集,20% 測試集劃分
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y_scaled, test_size=0.2, random_state=7)print("訓練集特征維度:", X_train.shape)
print("測試集特征維度:", X_test.shape)
print("訓練集目標維度:", y_train.shape)
print("測試集目標維度:", y_test.shape)輸出結果如下:
![]()

????????可以看出,進行基于Z-score方法的異常值處理之后,樣本數量由20940下降至16842,為后續模型構建的準確性打下基礎。
4. 模型構建
????????本實驗采用線性回歸、LASSO回歸、嶺回歸、彈性網回歸4類方法進行模型的構建,并以均方誤差 (Mean Squared Error, MSE)與決定系數 (R2 Score)作為模型的評估指標,最終選取效果最優的模型作為最終應用模型。
#(5)線性回歸
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,r2_score
LR = LinearRegression()
LR.fit(X_train,y_train)
# 預測
y_pred_linear = LR.predict(X_test)#評價
# 模型評估
print("Linear Regression:")
print("MSE:", mean_squared_error(y_test, y_pred_linear))
print("R^2 Score:", r2_score(y_test,y_pred_linear))#(6) LASSO 回歸(帶 L1 正則化)
from sklearn.linear_model import Lassolasso = Lasso(alpha=0.3, max_iter=10000)
lasso.fit(X_train, y_train)# 預測
y_pred_lasso = lasso.predict(X_test)# 模型評估
print("LASSO Regression:")
print("MSE:", mean_squared_error(y_test, y_pred_lasso))
print("R^2 Score:", r2_score(y_test, y_pred_lasso))
print("Coefficients:", lasso.coef_)#(7) 嶺回歸(帶 L2 正則化)
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0, max_iter=10000)
ridge.fit(X_train, y_train)# 預測
y_pred_ridge = ridge.predict(X_test)# 模型評估
print("Ridge Regression:")
print("MSE:", mean_squared_error(y_test, y_pred_ridge))
print("R^2 Score:", r2_score(y_test, y_pred_ridge))
print("Coefficients:", ridge.coef_)#(8) 彈性網回歸(L1 + L2 正則化)
from sklearn.linear_model import ElasticNetelastic_net = ElasticNet(alpha=1.0, l1_ratio=0.2, max_iter=10000)
elastic_net.fit(X_train, y_train)
# 預測
y_pred_elastic = elastic_net.predict(X_test)# 模型評估
print("Elastic Net Regression:")
print("MSE:", mean_squared_error(y_test, y_pred_elastic))
print("R^2 Score:", r2_score(y_test, y_pred_elastic))
print("Coefficients:", elastic_net.coef_)
輸出結果如下:
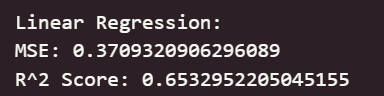
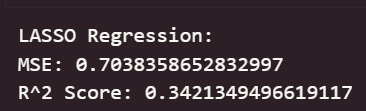
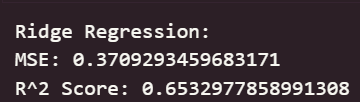
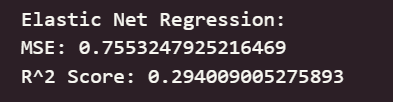
????????可以看出,在初始為調參的情況下,線性回歸模型與嶺回歸模型在測試集上取得了最佳的預測性能(最低的 RMSE 和最高的 R2 Score),這表明集成學習方法能夠有效學習加州房價數據中的復雜模式和特征交互。
5.模型參數調優(可視化對比)
由于線性回歸模型與嶺回歸參數較少,初始模型已是最優模型,故對LASSO回歸模型與彈性網模型進行參數調優。
#(9)lasso、彈性網模型參數調優
# 1、LASSO 模型
from sklearn.model_selection import GridSearchCVparam_grid_lasso = {'alpha': [0.001, 0.01, 0.1, 1.0, 10.0]}# LASSO 回歸參數范圍
lasso = Lasso(max_iter=10000)# 網格搜索
grid_lasso = GridSearchCV(lasso, param_grid_lasso, scoring='neg_mean_squared_error', cv=5)
grid_lasso.fit(X_train, y_train)# 最佳參數和最佳模型
best_lasso = grid_lasso.best_estimator_
y_pred_lasso_best = best_lasso.predict(X_test)print("LASSO - Best params:", grid_lasso.best_params_)
print("MSE after tuning:", mean_squared_error(y_test, y_pred_lasso_best))
print("R^2 Score after tuning:", r2_score(y_test, y_pred_lasso_best))# 2、ElasticNet 模型
param_grid_elastic = {'alpha': [0.001, 0.01, 0.1, 1.0, 10.0],'l1_ratio': [0.1, 0.3, 0.5, 0.7, 0.9]
}#ElasticNet 參數范圍elastic_net = ElasticNet(max_iter=10000)# 網格搜索
grid_elastic = GridSearchCV(elastic_net, param_grid_elastic, scoring='neg_mean_squared_error', cv=5)
grid_elastic.fit(X_train, y_train)# 最佳模型
best_elastic = grid_elastic.best_estimator_
y_pred_elastic_best = best_elastic.predict(X_test)print("ElasticNet - Best params:", grid_elastic.best_params_)
print("MSE after tuning:", mean_squared_error(y_test, y_pred_elastic_best))
print("R^2 Score after tuning:", r2_score(y_test, y_pred_elastic_best))plt.figure(figsize=(10, 10))# 調參前 LASSO
plt.subplot(2, 2, 1)
plt.scatter(y_test, y_pred_lasso, alpha=0.6)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')
plt.title('LASSO (Before Tuning)')
plt.xlabel('True Values')
plt.ylabel('Predictions')# 調參后 LASSO
plt.subplot(2, 2, 2)
plt.scatter(y_test, y_pred_lasso_best, alpha=0.6)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')
plt.title('LASSO (After Tuning)')
plt.xlabel('True Values')
plt.ylabel('Predictions')# 調參前 ElasticNet
plt.subplot(2, 2, 3)
plt.scatter(y_test, y_pred_elastic, alpha=0.6)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')
plt.title('ElasticNet (Before Tuning)')
plt.xlabel('True Values')
plt.ylabel('Predictions')# 調參后 ElasticNet
plt.subplot(2, 2, 4)
plt.scatter(y_test, y_pred_elastic_best, alpha=0.6)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')
plt.title('ElasticNet (After Tuning)')
plt.xlabel('True Values')
plt.ylabel('Predictions')plt.tight_layout()
plt.show()輸出結果如下:
![]()
![]()
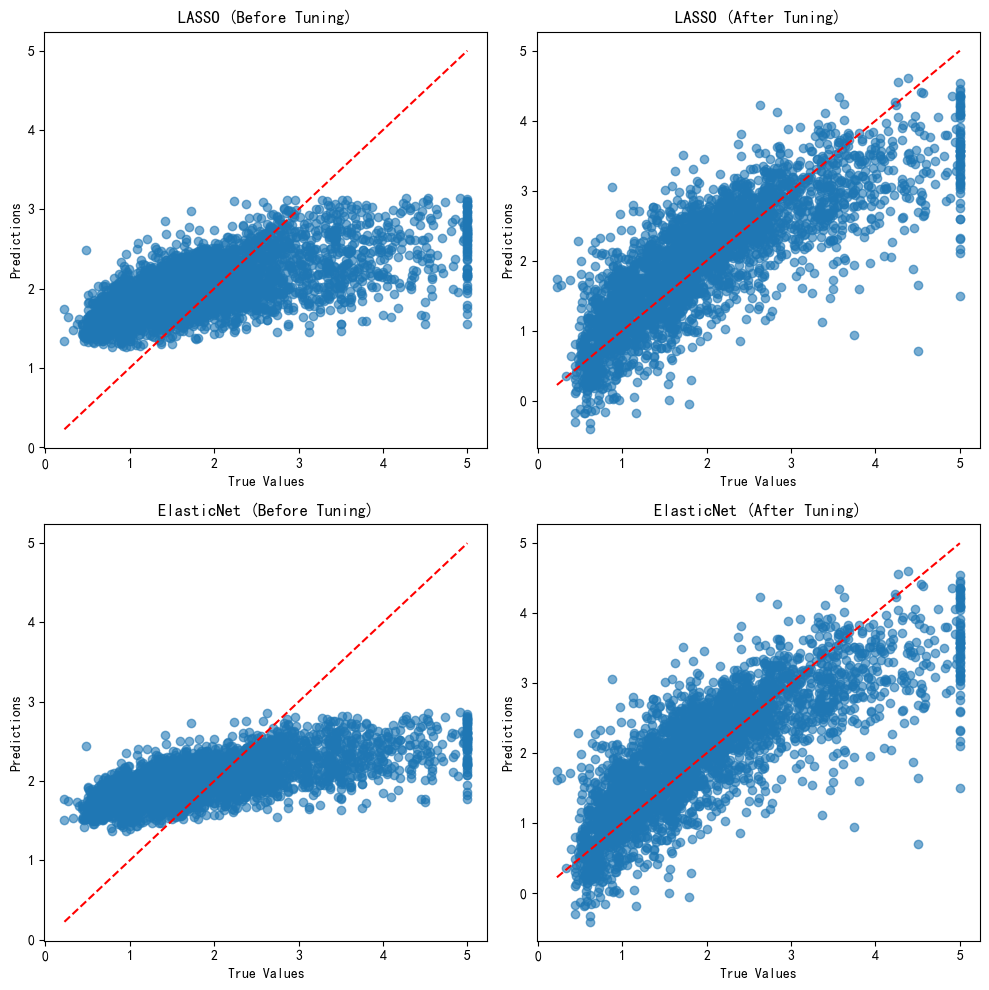
????????可以看出,相對初始模型,參數調優后的LASSO模型與彈性網模型在測試集的評價大幅上升,效果與線性回歸和嶺回歸相差無幾。
四、 結論
????????本實驗成功完成了加州房價預測的任務。通過數據加載、清洗、探索性分析和特征工程,為模型訓練準備了高質量的數據。通過嘗試不同的回歸模型,發現選擇的4類模型在該數據集上表現相差無幾,都可以相對準確地預測房價中位數。
改進方向:
進一步的特征工程:?可以嘗試創建特征之間的交互項或多項式特征,或許能進一步提升模型性能。
嘗試其他模型:?可以嘗試使用梯度提升樹(如?
XGBoost,?LightGBM)等更強大的集成模型。深入分析誤差:?分析預測誤差較大的樣本點,找出這些樣本的共同特征,有助于理解模型的局限性并指導下一步的優化。

的技術邏輯、核心價值與典型應用場景解析)

)

)
核心技術落地路徑與企業數字化轉型適配方案)

)










