三維變換

三種變換

下面分別是放縮，旋轉，平移


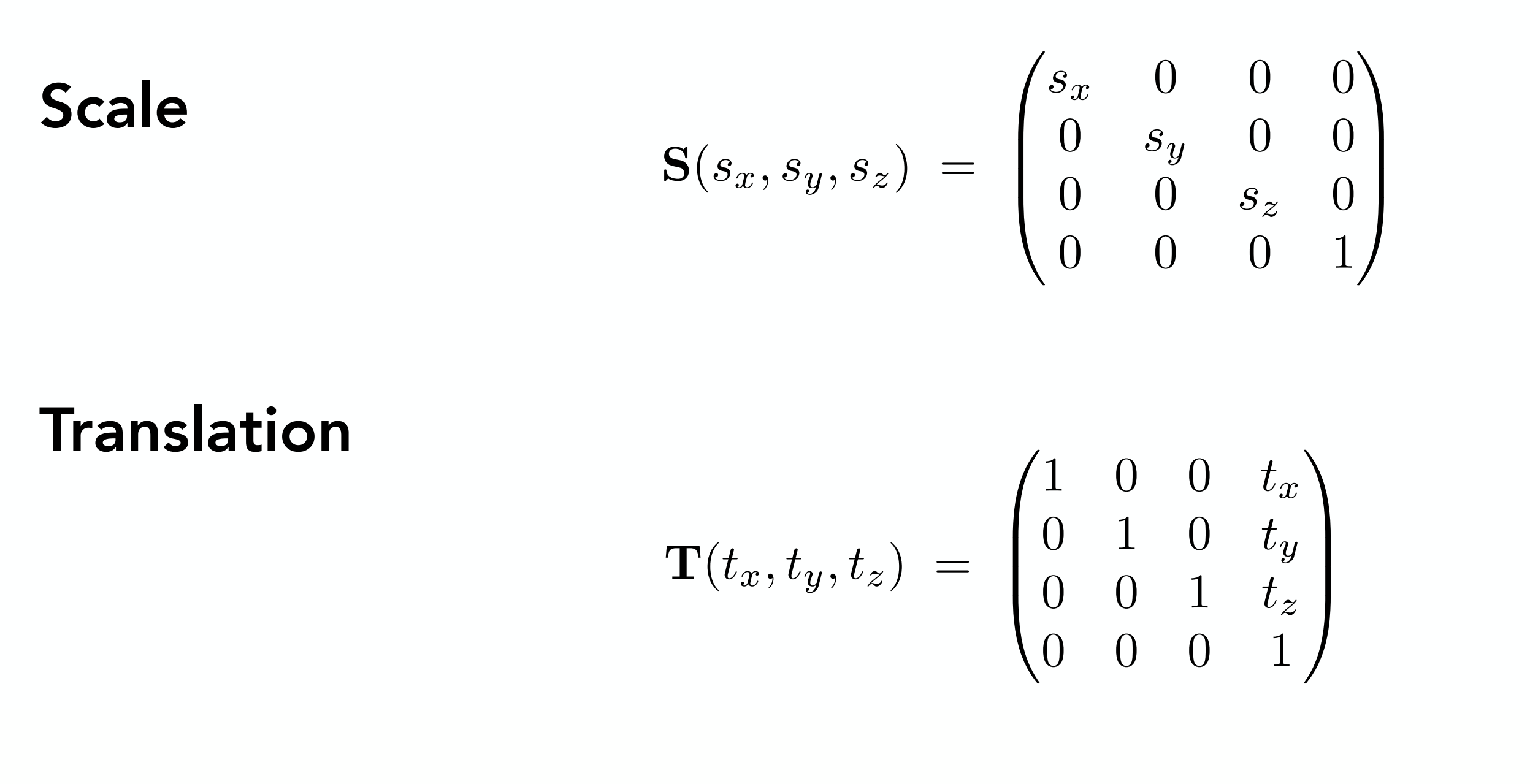
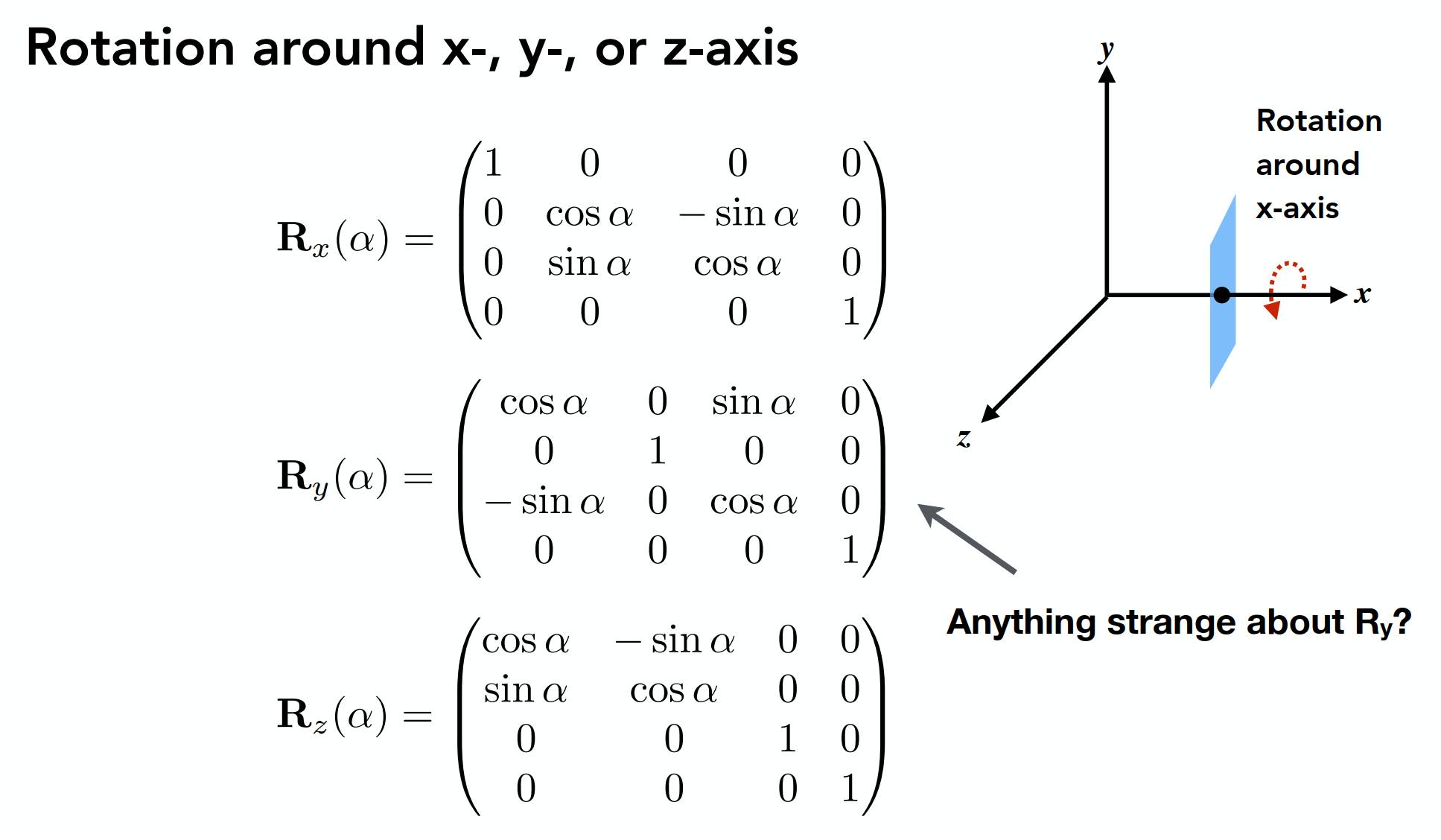
在旋轉當中，繞著y軸旋轉矩陣的順序不一樣，因為繞著y軸轉在右手坐標系中
，z是第一軸，x是第二軸，而負號會加在第一軸上，因此負號在下面。

羅德里格斯公式

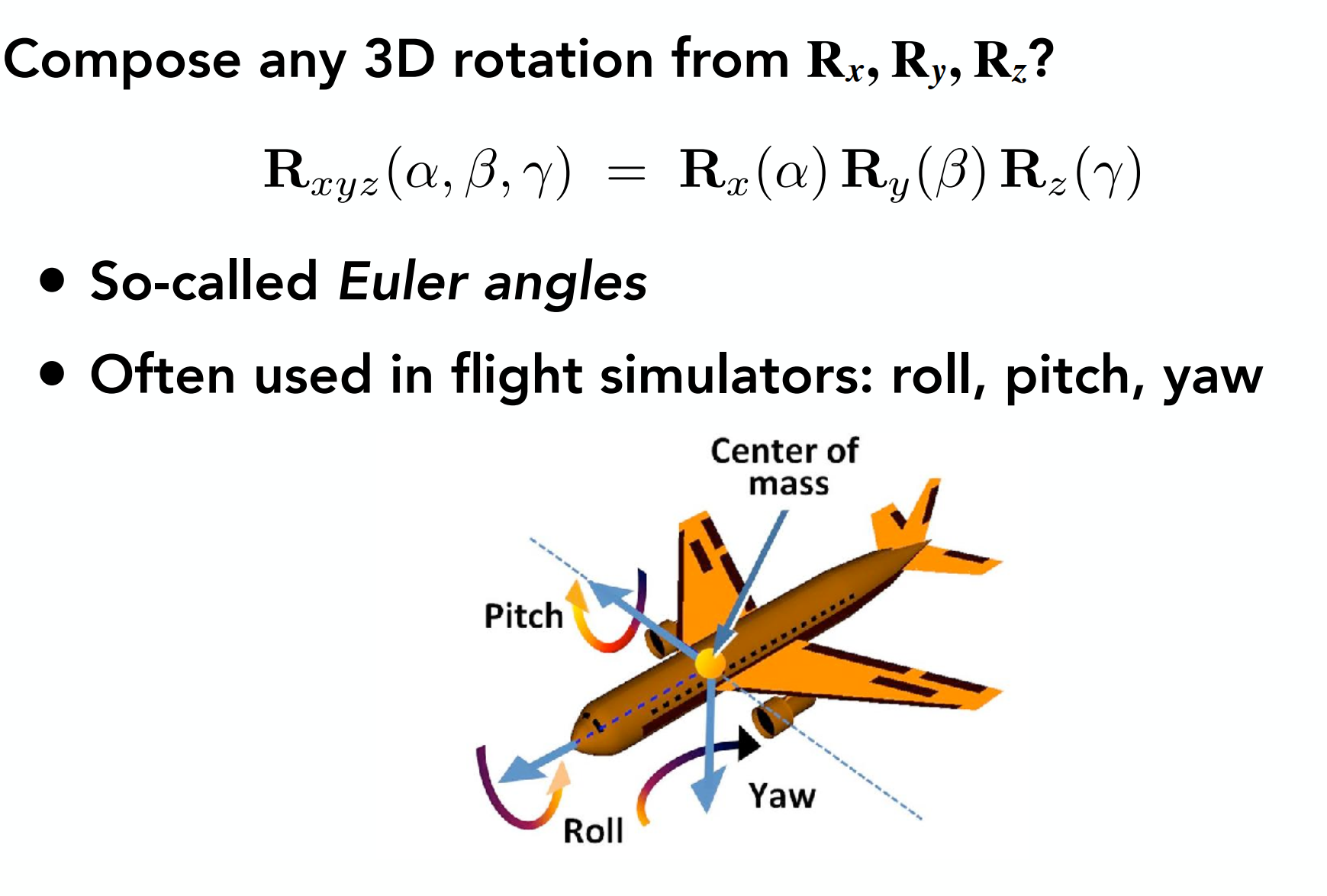
旋轉能夠分解成繞三軸旋轉的組合，如圖：

而羅德里格斯公式給出的是繞任意軸旋轉的公式：

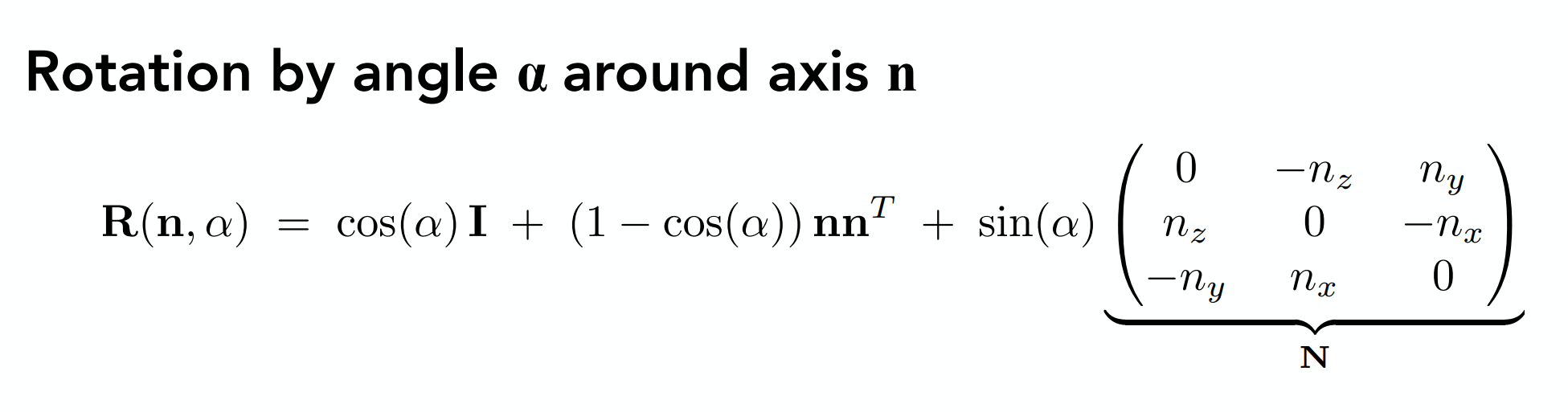
另外，旋轉矩陣并不方便做插值：15°的旋轉矩陣與25°的旋轉矩陣相加除二并不是20°，因此引入了四元數。

相機原理

此部分原Games101沒有，為更好展示變換場景引入：

相機成像

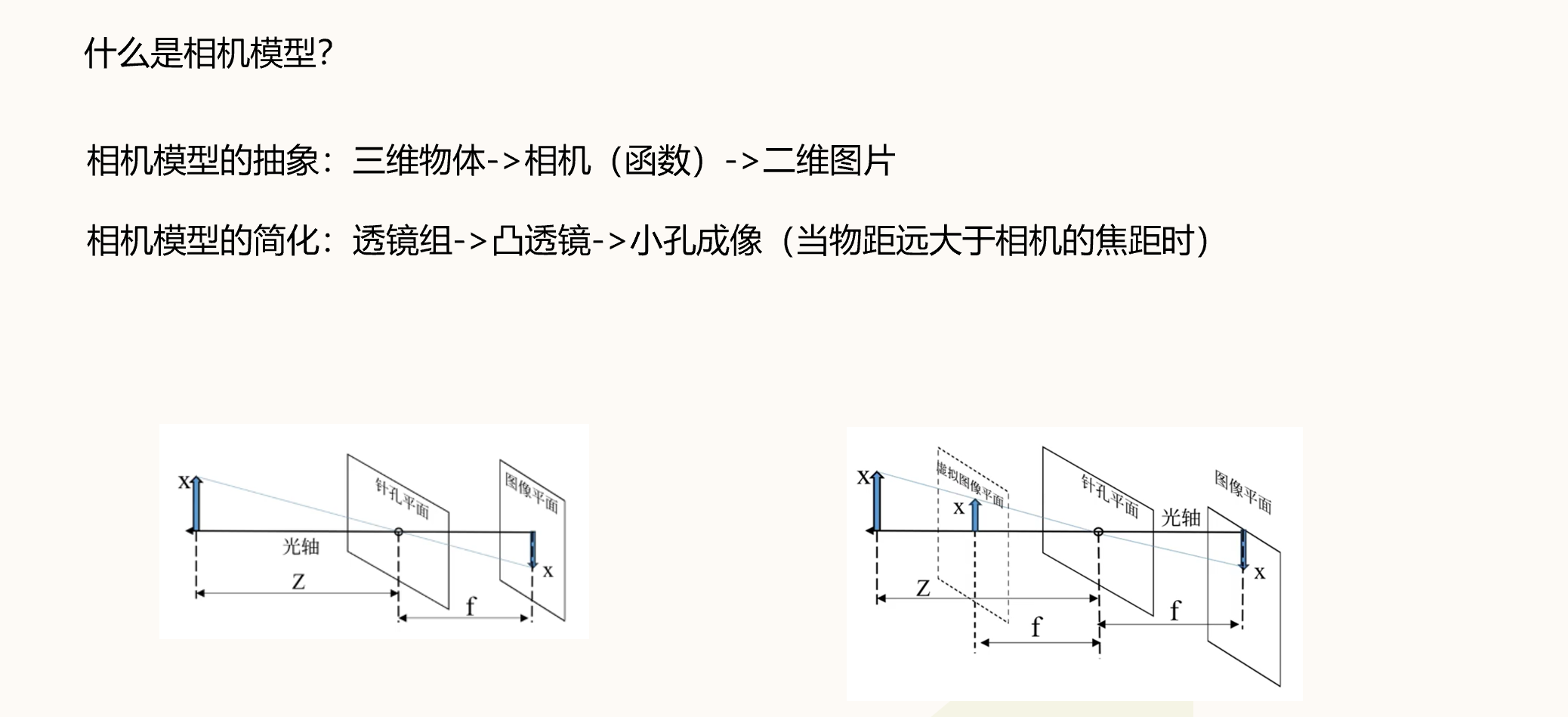
由上圖所示，相機模型可以看成小孔成像模型，而為了方便研究，一般將成像面對稱放到光心的前面，也就有了下圖：

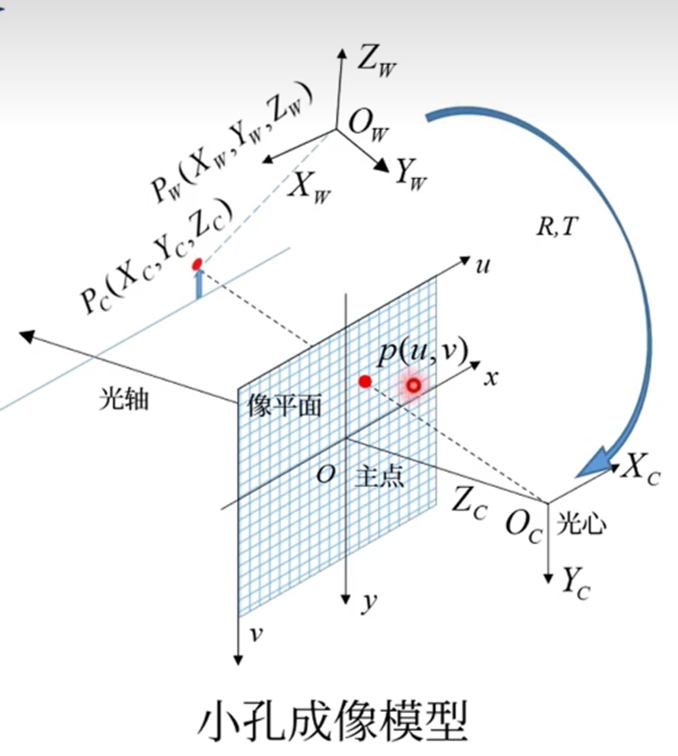
四大坐標系

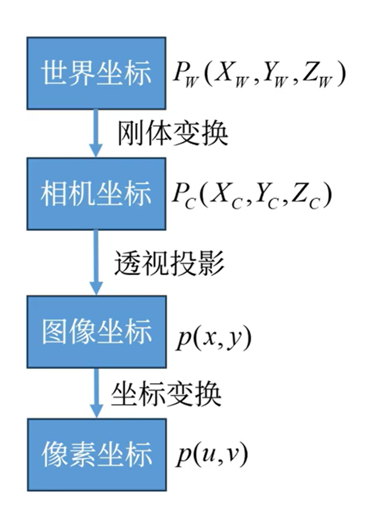
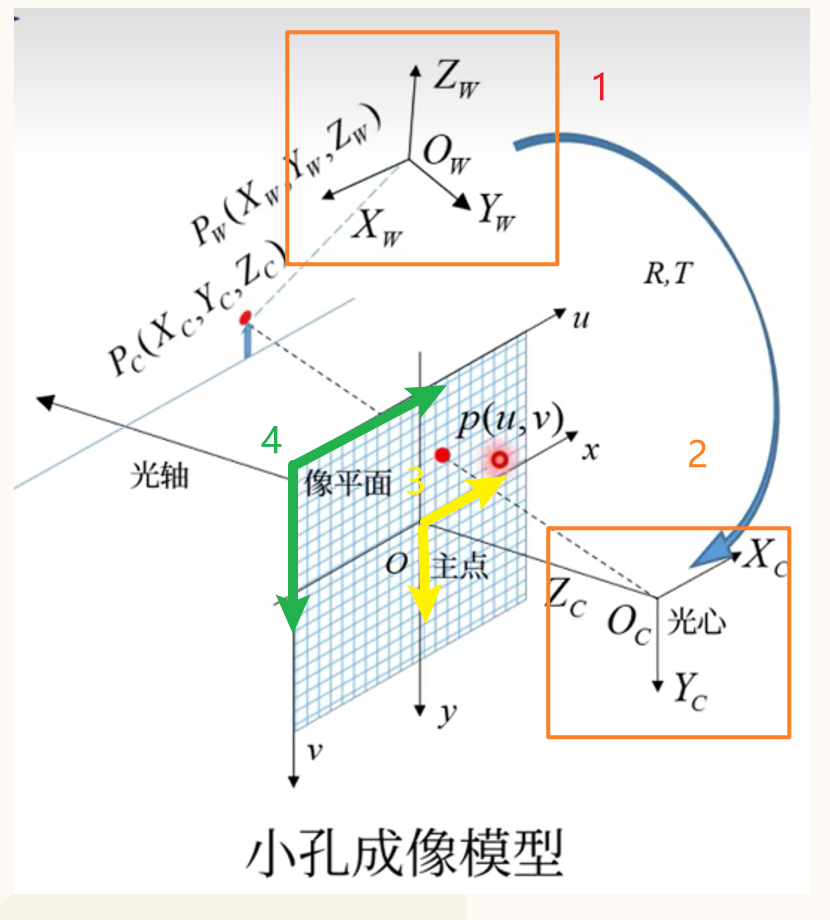
四大坐標系與圖中的編號一次對應

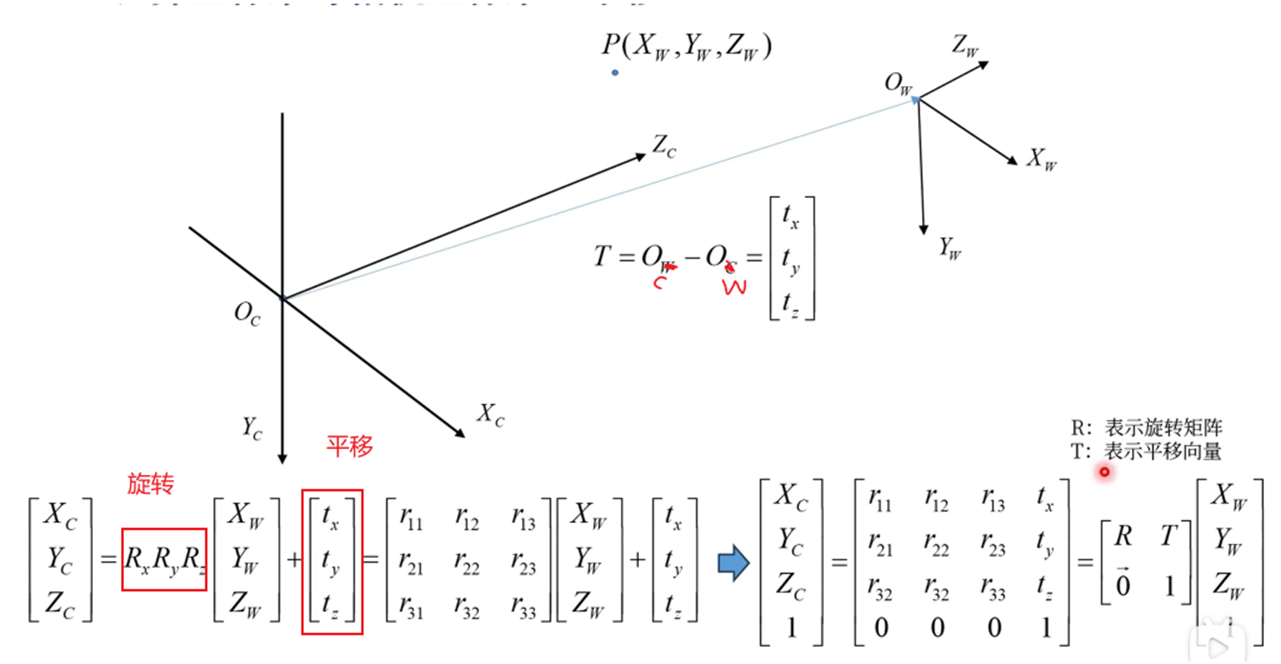
剛體變換（世界坐標->相機坐標）

剛體變換在圖形學中也稱觀測變換：
我們一般用三個向量描述攝像機的方向：

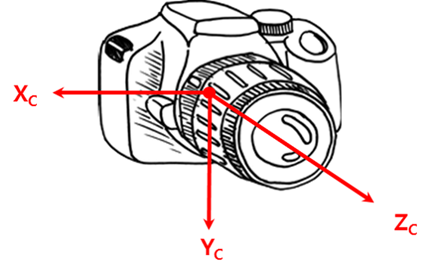
已知在世界坐標系下的位置和方向，將相機坐標坐標系原點即可完成觀測變換。

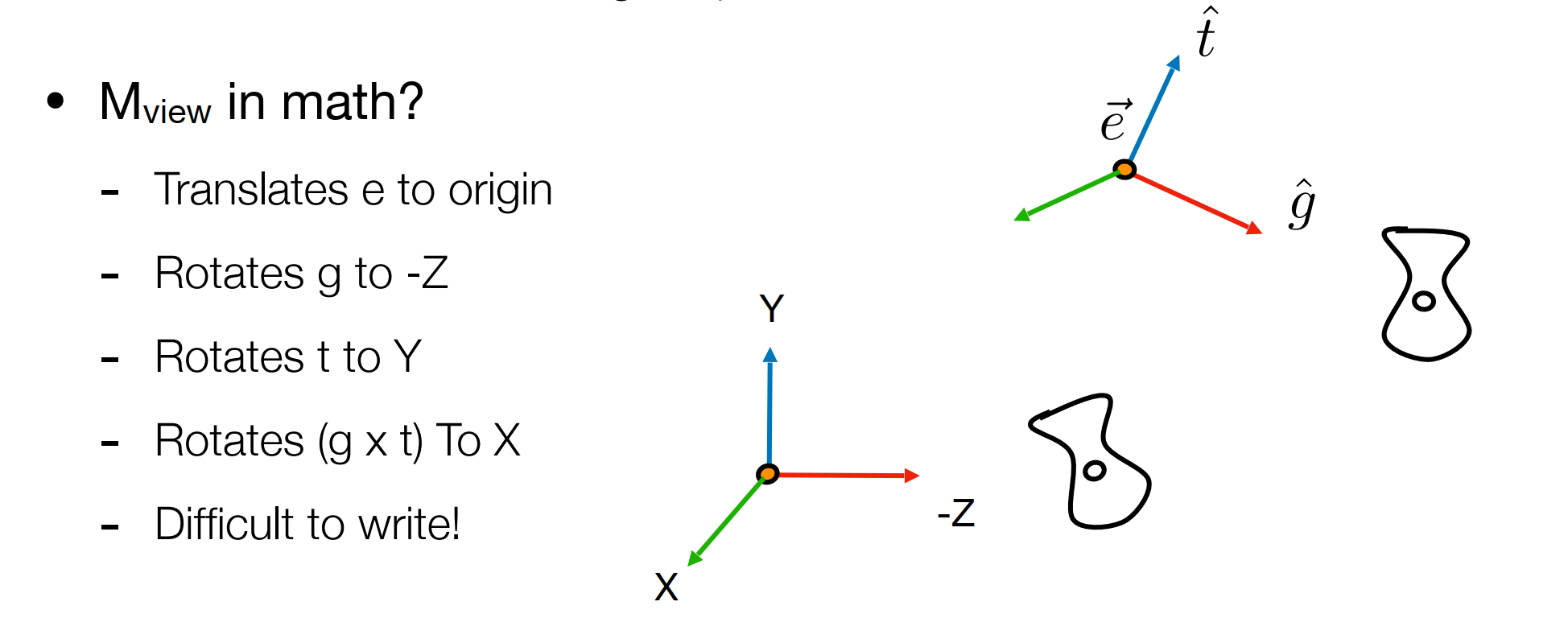
首先完成位置變換：先平移

然后完成旋轉：再旋轉

為方便先求旋轉矩陣的逆變換，在逆變換中x，y，-z三條軸均會變成攝像機方向的三個向量。又由于是正交矩陣（因為是剛體變換），矩陣的逆就是矩陣的轉置，由此求出。

透視變換與正交變換

由于攝像機其實是小孔成像（跟人眼一樣），因此會有近大遠小。

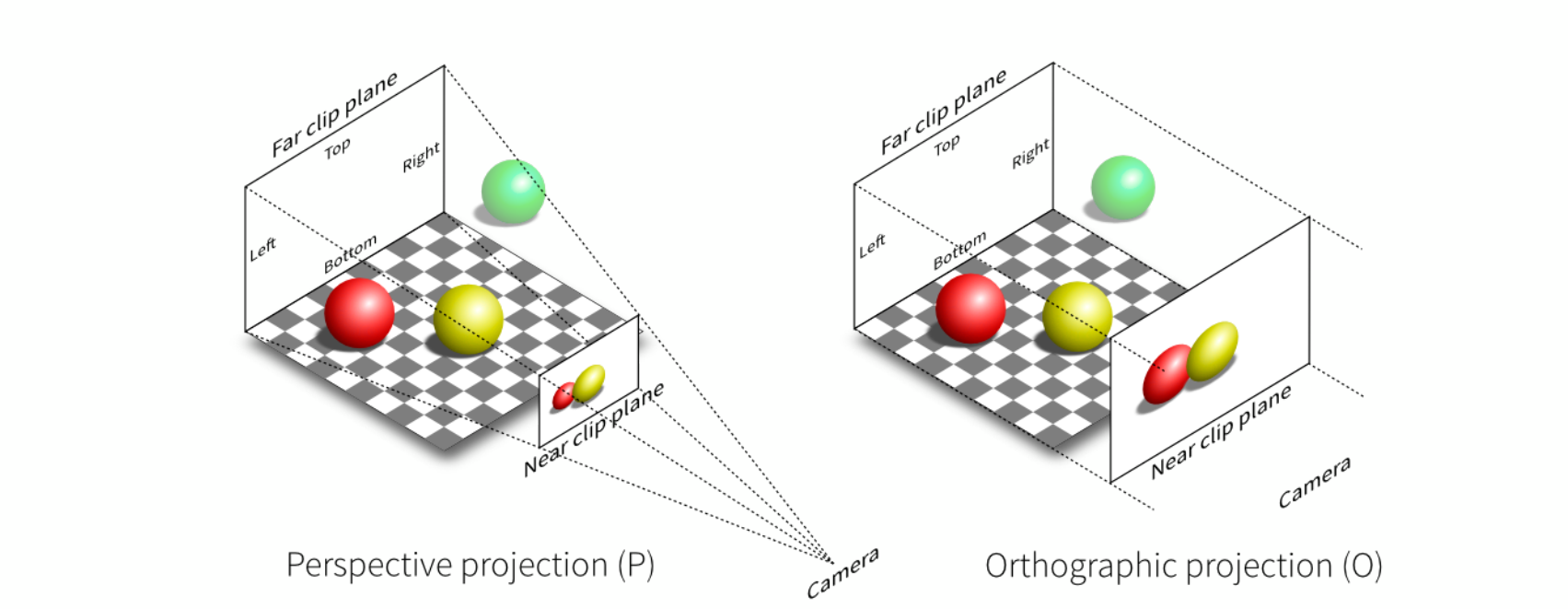
上圖中兩球大小相等，但在透視投影下大小由差異，而在正交投影下相同。
這是由于透視投影不同位置的光線進入光心的方向不同，不是平行的。

正交變換

在說明透視變換前先需要說明正交變換

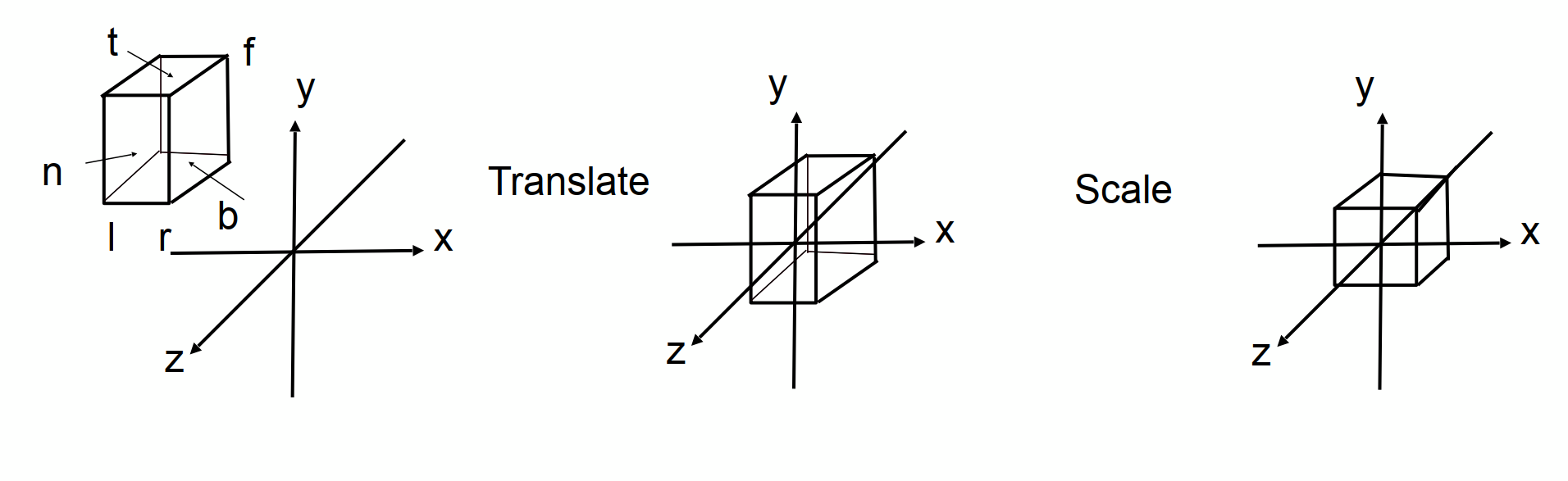
如圖所示，正交變換要做的事情其實是將要投影的空間壓縮成一個以原點為中心，邊長為2的立方體。
由此，定義空間的前后，左右，上下三組數據如圖所示，可得到如下的矩陣：

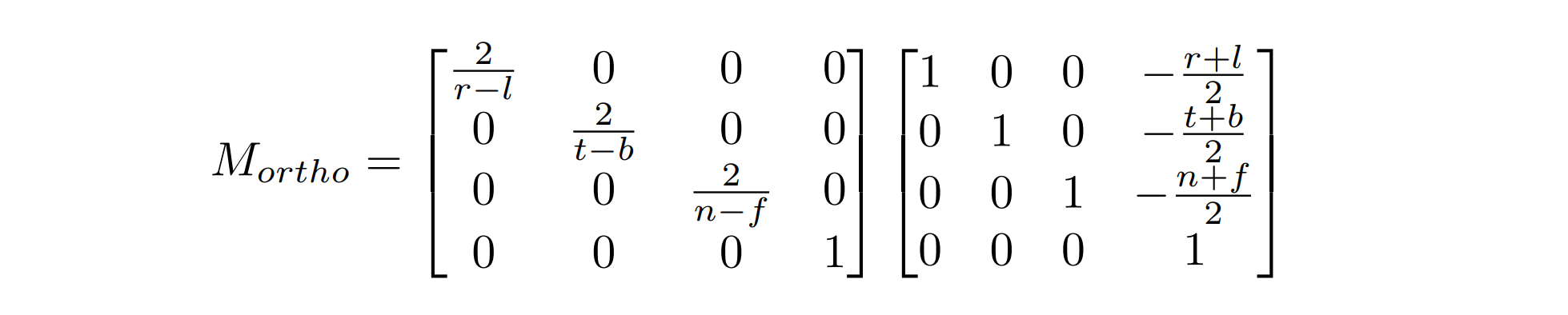
注意，由于z軸是負的，前后的順序是顛倒的。

投影變換

我們采用改良正交投影的方法實現透視投影。

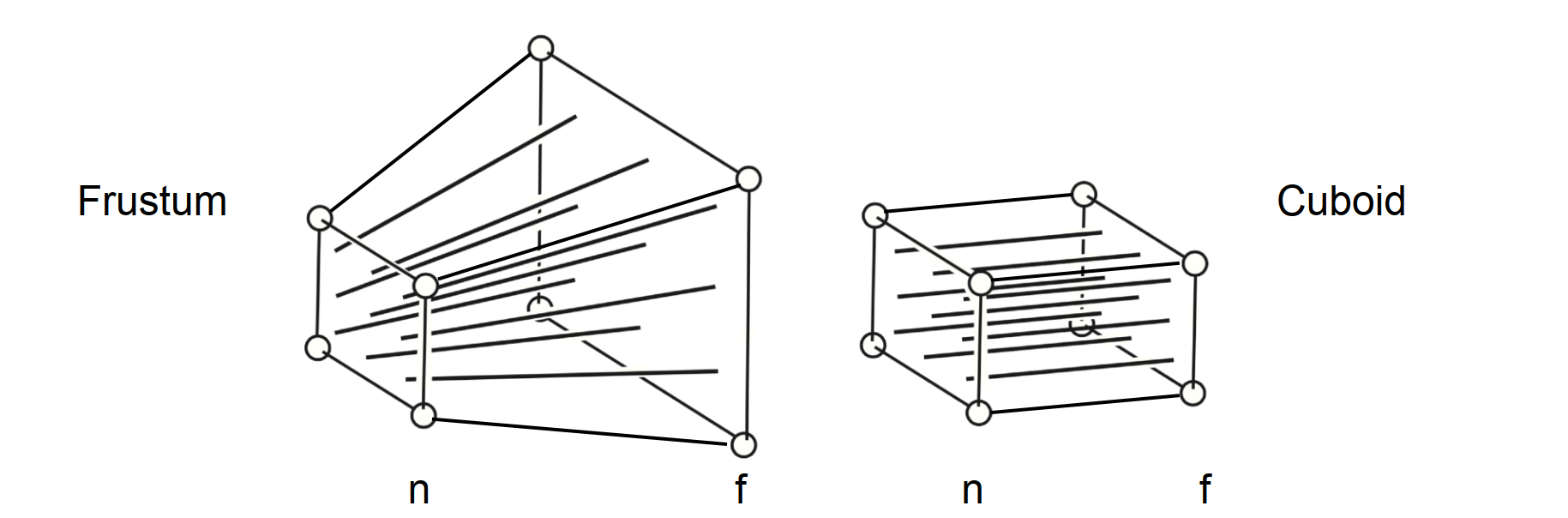
如圖所示，我們將原來是視錐的透視投影壓成一個長方體，也就是正交投影。
但是壓縮的方式不唯一，也就是不確定能壓成哪一個長方體。
因此在壓縮前需要確定幾個參數：

首先要確定兩個平面，近平面和遠平面，知道這兩個平面與原點的距離，分別為n和f。
然后確定這兩個平面的性質，近平面變換前后位置不變大小不變，原平面位置不變。
由此，我們列出以下式子：

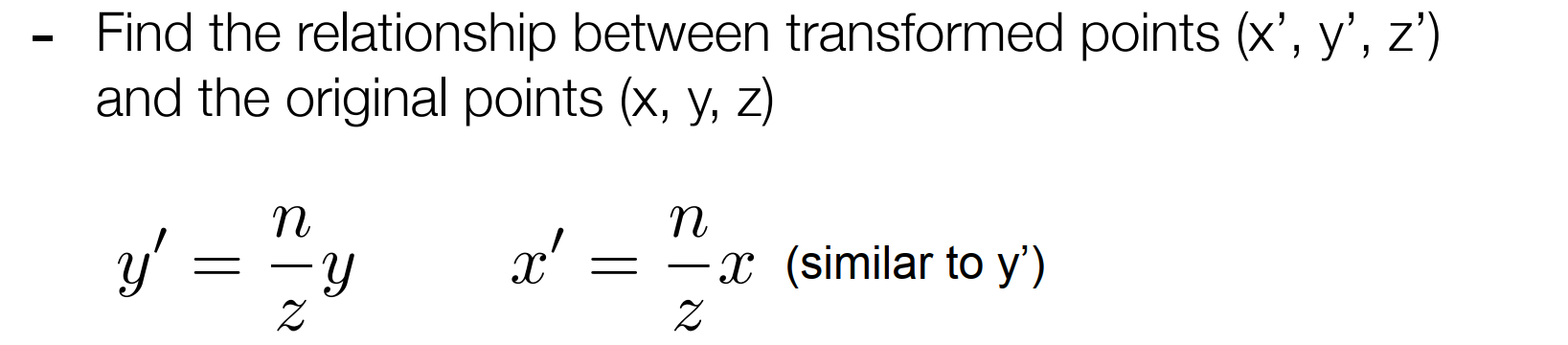
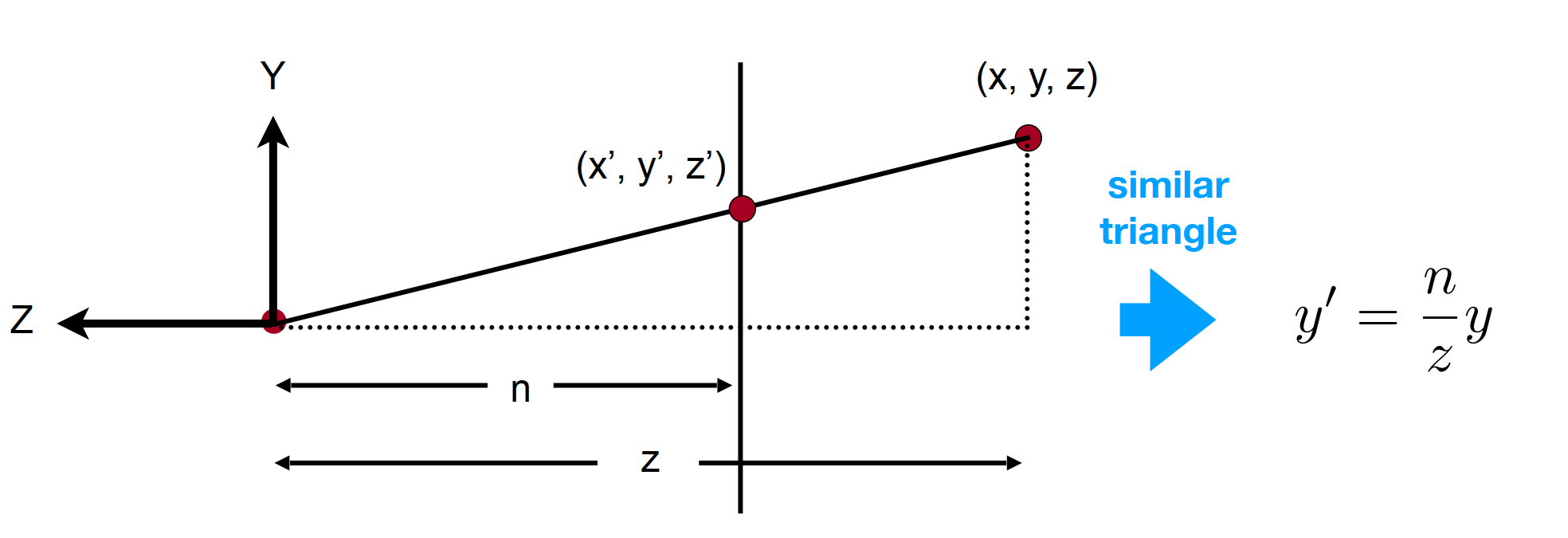
這里的z其實是n到f的任意一值

這樣就確定了這個矩陣的三行。
這一步利用的條件是變換后遠離近處的平面會變得和近處的平面一樣大（x，y方向上）。
然后，再利用近處的平面不變：將n帶入z

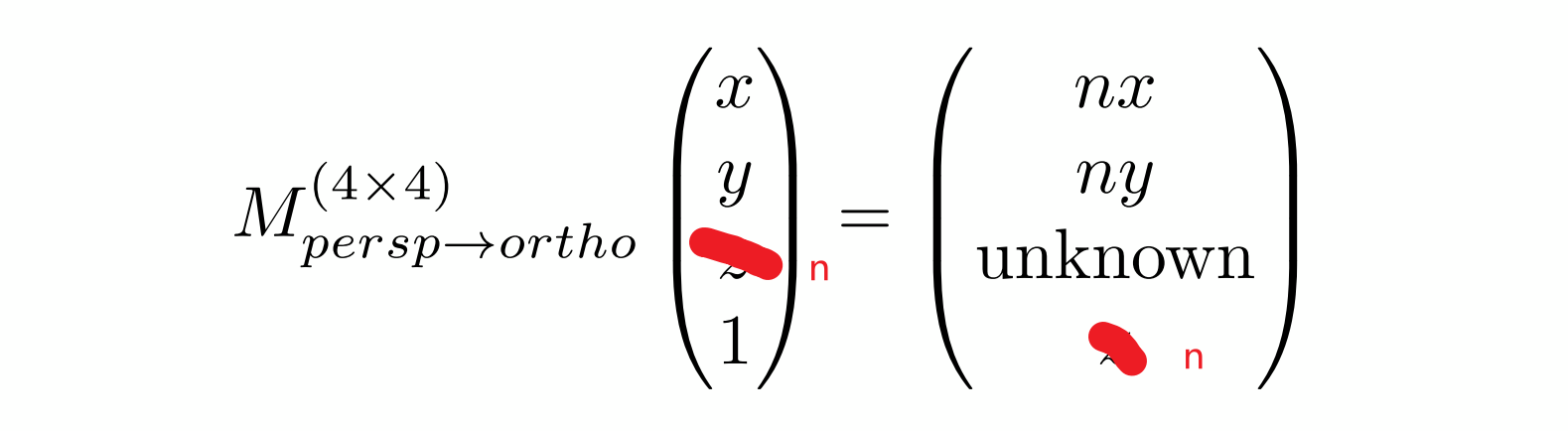
推斷出在近處，unknow是$n^2$,由此：

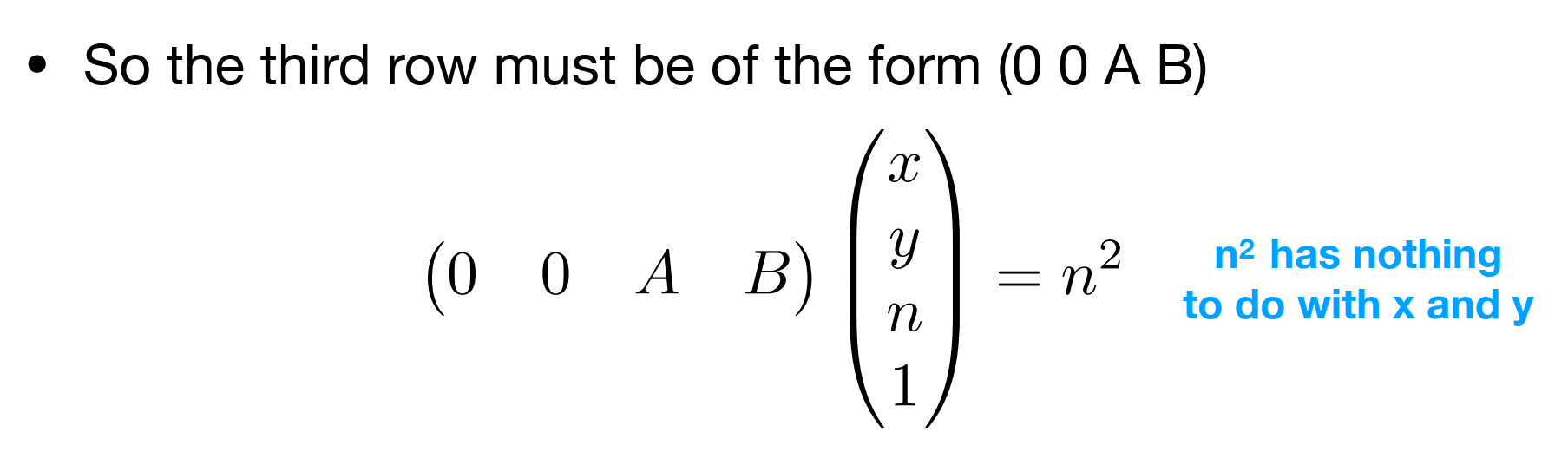
再由遠平面中心不變得：



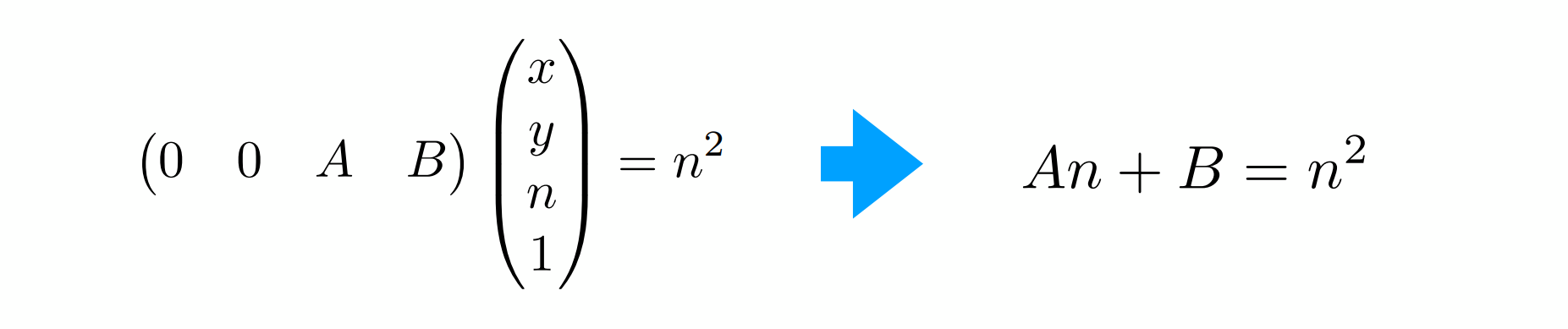
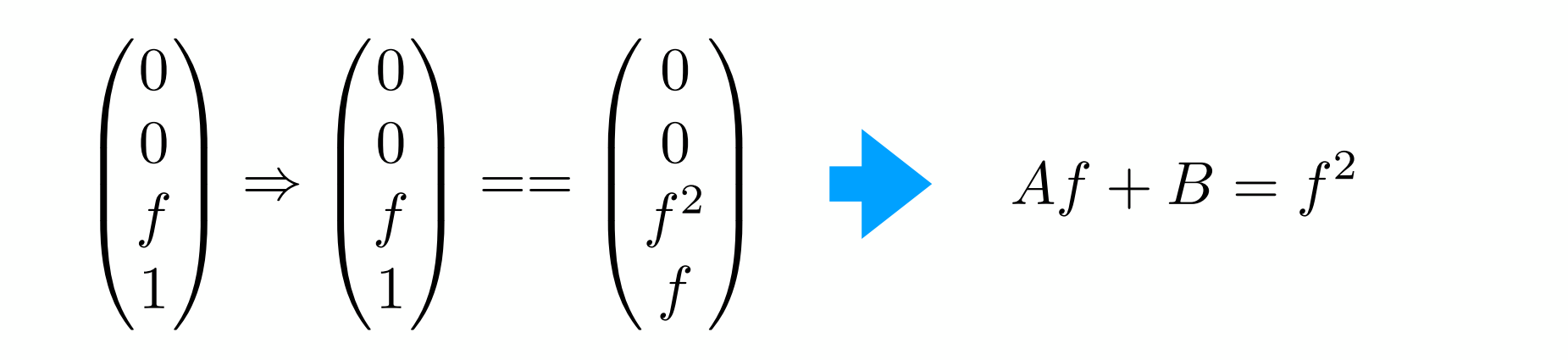
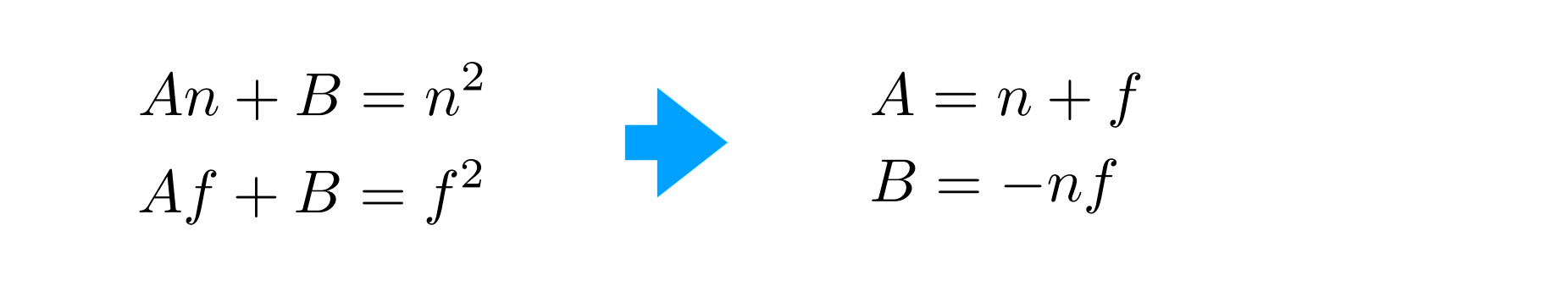
得：

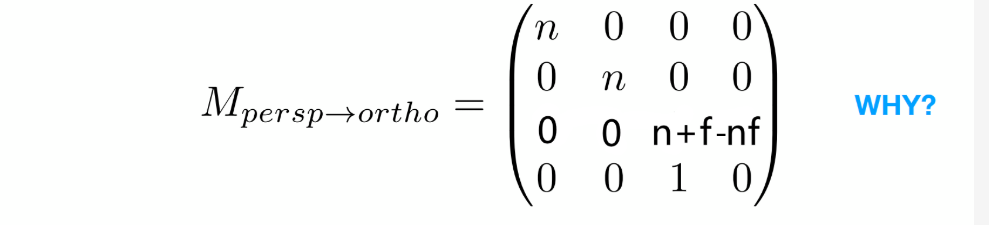
然后再進行正交投影。