今天筆者帶領讀者做幾道鏈式二叉樹OJ題目，希望讀者和筆者一起思考！

1.965. 單值二叉樹 - 力扣（LeetCode）

這道題思路不難想，首先知道單值二叉樹的定義：所有結點的值都相同，傳入的是第一個根節點root，然后考慮幾種情況，如果是NULL，那么這是一顆空樹，也 滿足單值二叉樹的要求，所以這種情況直接 返回true，然后考慮整個二叉樹，二叉樹有左子樹，右子樹，所以直接比較二叉樹一個結點的左右孩子結點即可，如果不等，那就返回false,如果相等，那就繼續往下比，下面展示一下筆者寫的代碼：

2.100. 相同的樹 - 力扣（LeetCode）

其實這道題目思路不難想到，無非就是先說特殊情況，然后進行一些遞歸操作即可：

3.101. 對稱二叉樹 - 力扣（LeetCode）

還是老規矩，先判斷為空，之后為了方便，我們封裝一個輔助函數，然后返回的情況其實就很顯然了：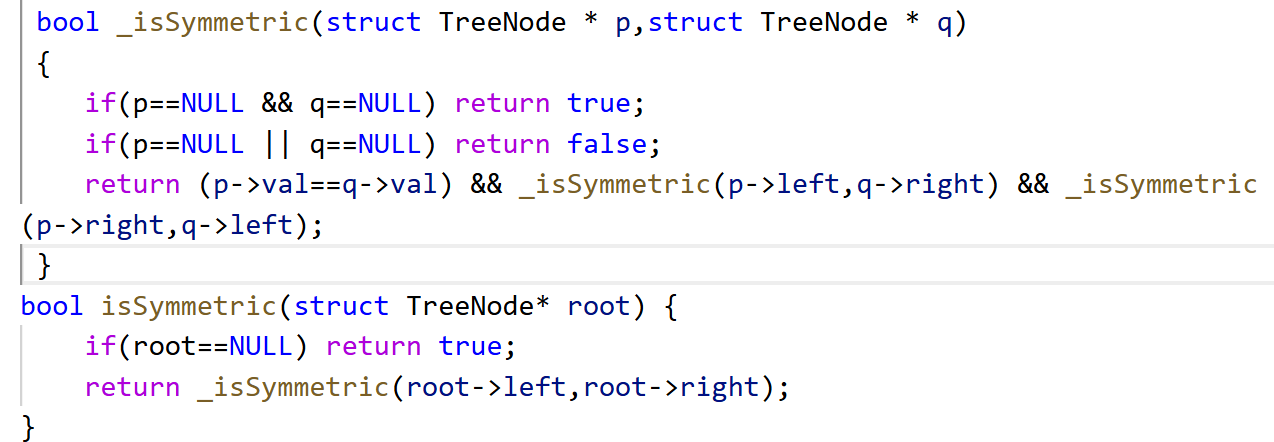

4.144. 二叉樹的前序遍歷 - 力扣（LeetCode）

由于前序中序后序遍歷并無太大 差別，故筆者著重詳解一下前序遍歷，中序后序留給讀者自行練習。這道題首先需要先理解題意，其實意思就是讓我們用一個數組存儲這個二叉樹按照前序遍歷的順序訪問的結點，所以觀察需要完成的函數，我們需要提供一個returnsize,這其實是由于leetcode的原因，傳數組時必須把數組的大小也傳進去，也叫輸出型參數，綜上所述，我們需要單獨求出數組的大小，而這這個數組的求法顯然需要用malloc函數，創建完數組之后就需要考慮進行前序遍歷，下面先給讀者看一下筆者的代碼：

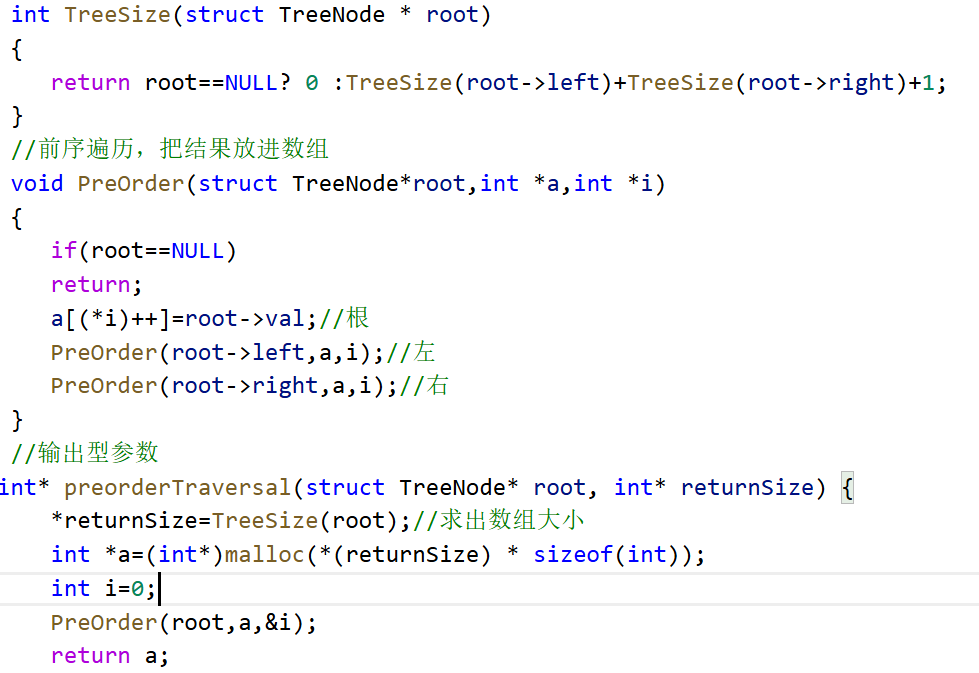
筆者首先求了一個TreeSize,這是因為后面申請內存的時候不會造成浪費，這里需要記住的是returnSize是一個 指針，需要解引用才能當作數組，然后一個很易錯的點就是i，相信讀者會有 一個問題，為什么i要傳入一個指針呢？為什么不能直接傳入i呢？其實這個問題在之前的文章中筆者提到過，遞歸實際上是棧幀問題，通俗理解就是每個副本都會有一個新的i，那些不用的副本中的i始終從1開始，這就會導致混亂，因此需要傳入指針，可以理解為傳入指針會讓根本改變，因為地址找到的東西是固定的，相信到這讀者都能理解筆者這么寫的原因了。

5.94. 二叉樹的中序遍歷 - 力扣（LeetCode）

6.145. 二叉樹的后序遍歷 - 力扣（LeetCode）

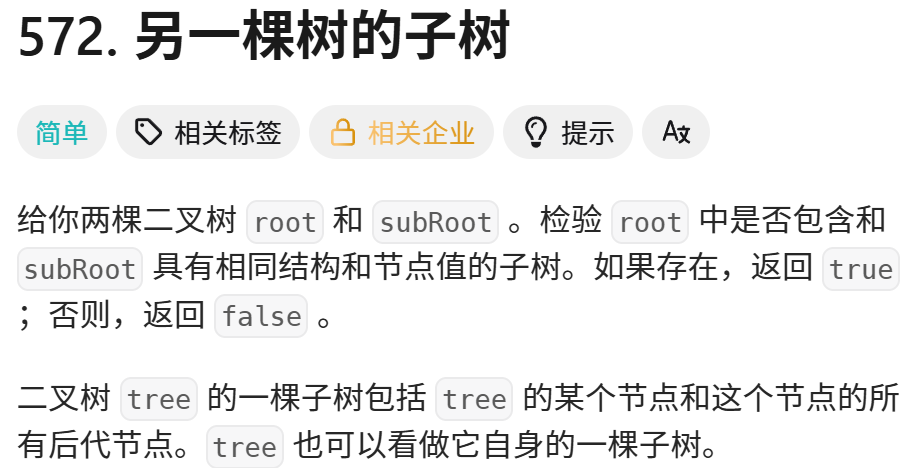
7.572. 另一棵樹的子樹 - 力扣（LeetCode）

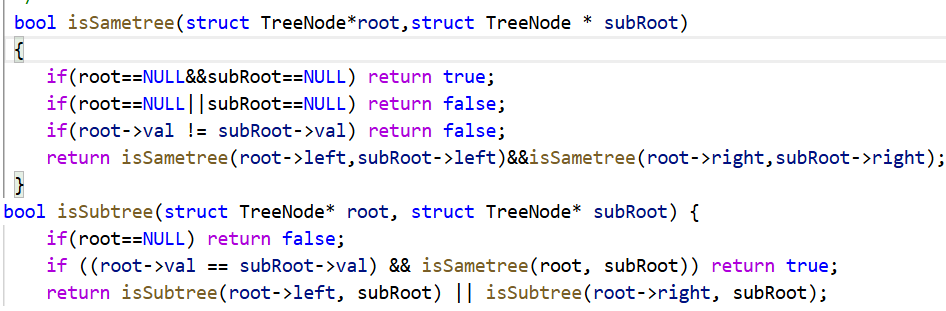
以筆者的習慣，還是先看題目給的函數，傳入了兩個指針。先判斷第一種情況，二者是不是一棵樹，如果是一棵樹的話那么直接返回true即可，然后就是root為空結點的情況，空結點直接返回false即可，因為空樹不可能有子樹，然后就是很正常的遞歸操作了，和之前同理，即可，下面給讀者看一下筆者的代碼：

8.二叉樹遍歷_牛客題霸_牛客網

ok,這就是本文的最后一道題，這道題比較綜合，不難理解，這道題的本質是先按照前序創一個二叉樹，然后中序遍歷，把遍歷結果儲存起來，其實這道題就是把之前講過的東西結合在了一起，讀者自行完成。