Delay Tolerant Networks – DTNs 延遲容忍網絡架構
- 歸屬
- Delay Tolerant Networks – DTNs 延遲容忍網絡
- 應用實例
- 例子 1:瑞典北部的薩米人 (Saami reindeer herders)
- 例子 2:太平洋中的動物傳感網絡
- DTNs路由方式——存儲&轉發
- DTNs移動模型
- Random walk 隨機游走
- Gauss-Markov Mobility 高斯-馬爾可夫移動性
- Random waypoint 隨機航點
- Epidemic Routing(流行病路由)——DTNs框架下的路由協議
- PRoPHET路由協議——DTNs框架下的流行病改進路由協議
- 核心思想
- 概率更新公式
- 📊 與 Epidemic Routing 對比
- PRoPHET 協議 — 傳遞性 (Transitivity)
- 概率更新公式
- PRoPHET 協議(以及 DTN 路由)中的“權衡 (Trade-off)”
- 多復制 vs 少復制
- 設置閾值 (Threshold) 轉發
- 解決方案
- 具體實例
歸屬
延遲容忍網絡不屬于Data-centric / Hierarchical / Geographical / QoS-based這 4 類里的任何一個。
Data-centric / Hierarchical / Geographical / QoS-based 默認網絡端到端連通、可以逐跳轉發;而 DTN 的前提恰好相反:長時延、間歇性連接,用 store–carry–forward(存-攜-轉) 的“機會式/容斷”路由范式。所以它通常被單列為 Delay/Disruption-Tolerant(Opportunistic)路由 一大類。
Delay Tolerant Networks – DTNs 延遲容忍網絡
DTN(Delay/Disruption Tolerant Networks,延遲/容斷網絡)是一類 能夠在高時延、大誤碼率、頻繁斷連、甚至無持續端到端路徑的環境下 仍然提供數據傳輸服務的網絡體系結構。
核心特征:
采用 store–carry–forward(存儲–攜帶–轉發) 的路由模式:
當節點之間沒有即時可用的鏈路時,節點會先將消息存儲在本地緩存中;
當未來遇到合適的轉發機會(例如節點移動到有連接的位置),再將消息轉發出去;
通過多次這樣的“存–攜–轉”,最終消息能夠到達目的地。
應用實例
DTN – 間歇性連接的 WSN(或自組織網絡),其中信息路由延遲是可以容忍的,→存儲和轉發
例子 1:瑞典北部的薩米人 (Saami reindeer herders)
環境:生活在北極圈附近,地廣人稀,通信設施不足。
做法:在 雪地摩托 上裝移動中繼,牧民移動時攜帶數據。
應用:牧民的電子郵件、網頁緩存等數據通過“存–攜–轉”的方式帶回網絡覆蓋區,再投遞。
👉 說明 DTN 可用于偏遠地區人群的基本通信服務。
例子 2:太平洋中的動物傳感網絡
環境:給 海豹、鯨魚等動物佩戴溫度/位置傳感器,幫助測量海洋溫度
問題:動物在大洋中移動,節點之間的連接是 間歇性的。
做法:利用動物偶爾相遇時交換/轉發數據,最終把數據帶到基站(sink)
👉 說明 DTN 可利用“節點移動+偶遇”來完成數據收集。
DTNs路由方式——存儲&轉發
類似于郵政服務→存儲和轉發,節點的移動性可以被利用

DTNs移動模型
Random walk 隨機游走
節點選擇移動方向,介于 0 和 2π2π2π 之間,以及給定分布的速度; 例如,均勻、正態分布。
節點以該速度沿該方向(公式如下) 移動指定距離或一段時間。在此期間結束時,節點重復此過程。

Gauss-Markov Mobility 高斯-馬爾可夫移動性
節點的速度和方向在第 nnn 時刻由前一時刻、均值以及隨機變量共同決定:
sn=αsn?1+(1?α)sˉ+1?α2sxn?1s_n = \alpha s_{n-1} + (1-\alpha)\bar{s} + \sqrt{1-\alpha^2}\,s_{x_{n-1}} sn?=αsn?1?+(1?α)sˉ+1?α2?sxn?1??
dn=αdn?1+(1?α)dˉ+1?α2dxn?1d_n = \alpha d_{n-1} + (1-\alpha)\bar{d} + \sqrt{1-\alpha^2}\,d_{x_{n-1}} dn?=αdn?1?+(1?α)dˉ+1?α2?dxn?1??
其中:
- sns_nsn? :第 nnn 時刻的速度
- dnd_ndn? :第 nnn 時刻的方向
- sˉ,dˉ\bar{s}, \bar{d}sˉ,dˉ :平均速度和平均方向
- sxn?1,dxn?1s_{x_{n-1}}, d_{x_{n-1}}sxn?1??,dxn?1?? :來自高斯分布的隨機變量 (隨機性由此項產生)
- α\alphaα :調節隨機性的參數(000 = 隨機游走,111 = 線性運動)
Random waypoint 隨機航點
每個節點選擇特定區域內的隨機點作為其目的地,節點以其選定的速度移動到其目的地。 當節點到達其目的地時,它會停止一段時間,之后它選擇一個新的目的地和速度并恢復移動。
第 nnn 時刻節點的位置:
xn=xn?1+sn?1cos?(dn?1)x_n = x_{n-1} + s_{n-1}\cos(d_{n-1}) xn?=xn?1?+sn?1?cos(dn?1?)
yn=yn?1+sn?1sin?(dn?1)y_n = y_{n-1} + s_{n-1}\sin(d_{n-1}) yn?=yn?1?+sn?1?sin(dn?1?)
其中:
- sn?1s_{n-1}sn?1? :第 n?1n-1n?1 時刻的速度
- dn?1d_{n-1}dn?1? :第 n?1n-1n?1 時刻的方向 [0,2π][0,2π][0,2π]
- x,yx,yx,y :坐標位置

Epidemic Routing(流行病路由)——DTNs框架下的路由協議
Based on the theory of epidemic algorithms 基于疫情算法理論
特征:
節點之間相遇時成對交換消息,最終將消息傳遞到目的地
假設隨機移動性模型
核心思想:像病毒傳播一樣,讓消息在節點相遇時被復制并擴散,直到傳到目的地。
當兩個節點相遇時:
交換 summary vector(各自存有哪些消息的索引)。
根據缺失情況請求和發送消息。
節點緩存(buffer)里保存消息。

消息簡單結構:全網唯一ID用于識別節點,TTL(生存時間)保證消息不要過度泛濫。

如果緩沖區和 TTL 足夠大,則消息會分布在整個網絡中,并且傳遞概率非常高。
如果 TTL = 1,則消息僅傳遞到目標(如果遇到)
PRoPHET路由協議——DTNs框架下的流行病改進路由協議
PRoPHET (Probabilistic Routing Protocol using History of Encounters and Transitivity)
PRoPHET 是一種 DTN 路由協議,改進自 Epidemic Routing。
它利用 節點歷史相遇信息 和 轉遞性 (transitivity),計算消息的投遞概率,從而選擇性復制消息,減少資源消耗。
核心思想
- 每個節點維護一個投遞概率表 P(a,b)P(a,b)P(a,b),表示 節點 aaa 把消息送到節點 bbb 的可能性。
- P(a,b)∈[0,1]P(a,b) \in [0,1]P(a,b)∈[0,1]
- 當兩個節點相遇時,交換:
- Summary Vector(消息摘要)
- Delivery Predictability Vector(投遞概率信息)
- 只把消息交給 投遞概率更高 的節點。
概率更新公式
當節點 aaa 與節點 bbb 相遇時,更新 P(a,b)P(a,b)P(a,b):
P(a,b)=P(a,b)old+(1?P(a,b)old)×PinitP_{(a,b)} = P_{(a,b)_{old}} + \big(1 - P_{(a,b)_{old}}\big) \times P_{init} P(a,b)?=P(a,b)old??+(1?P(a,b)old??)×Pinit?
其中:
- P(a,b)oldP_{(a,b)_{old}}P(a,b)old?? :舊的投遞概率
- PinitP_{init}Pinit? :初始化常數,每次相遇時增加預測值
- 相遇次數越多,P(a,b)P(a,b)P(a,b) 越大
📊 與 Epidemic Routing 對比
- Epidemic:見面就復制 → 泛洪式擴散,消耗大
- PRoPHET:基于概率選擇性復制 → 更高效
PRoPHET 協議 — 傳遞性 (Transitivity)
在 PRoPHET 協議中,如果節點 a 沒有直接遇到節點 c,但是它經常遇到節點 b,而節點 b 又經常遇到節點 c,
那么可以認為 a 通過 b 也有一定概率把消息送到 c。這就是 傳遞性 (transitivity) 的思想。
概率更新公式
P(a,c)=P(a,c)old+(1?P(a,c)old)×P(a,b)×P(b,c)×βP_{(a,c)} = P_{(a,c)_{old}} + \Big(1 - P_{(a,c)_{old}}\Big) \times P_{(a,b)} \times P_{(b,c)} \times \beta P(a,c)?=P(a,c)old??+(1?P(a,c)old??)×P(a,b)?×P(b,c)?×β
其中:
- P(a,c)oldP_{(a,c)_{old}}P(a,c)old?? :a 到 c 的舊投遞概率
- P(a,b)P_{(a,b)}P(a,b)? :a 到 b 的投遞概率
- P(b,c)P_{(b,c)}P(b,c)? :b 到 c 的投遞概率
- β\betaβ :傳遞性衰減因子,0<β<10 < \beta < 10<β<1
b 是 a 的一個良好中繼 (relay):如果 a→b、b→c 的概率都高,那么 a→c 的概率也會增加。
衰減因子 β:避免因為多級傳遞導致概率無限放大。
總結: PRoPHET 協議利用 直接相遇、老化機制、傳遞性 三個更新規則,動態調整消息的投遞概率,從而比 Epidemic 路由更高效。
PRoPHET 協議(以及 DTN 路由)中的“權衡 (Trade-off)”
多復制 vs 少復制
如果 把消息轉發給多個節點(例如 a→b, a→d, a→e),消息最終到達目的地 c 的概率更大。
但問題是:消耗更大(帶寬、緩存、能耗)。
👉 這是 高投遞率 和 高開銷 的權衡。

設置閾值 (Threshold) 轉發
選擇固定閾值,僅將消息轉發到目標具有傳遞可預測性>閾值的節點 →如果稍后遇到具有更高可預測性的節點怎么辦?

解決方案
規則
當兩個節點相遇時,如果對方節點到目標的 投遞概率更高,就把消息轉發給對方。
如果緩沖區滿了,可以用隊列管理(比如 FIFO)丟掉舊消息。

Time 1
節點 a 手里有一個要發給 c 的消息。它遇到了節點 g。
因為 P(g,c)>P(a,c)P(g,c) > P(a,c)P(g,c)>P(a,c)(g 到 c 的概率比 a 更高),所以 a 把消息轉給 g。

Time 2
之后,a 又遇到了節點 e。
P(e,c)>P(a,c)P(e,c) > P(a,c)P(e,c)>P(a,c),所以 a 再把消息轉給 e。
而且 P(e,c)>P(g,c)P(e,c) > P(g,c)P(e,c)>P(g,c),所以 e 比 g 更適合作為中繼。
最終 e 把消息傳給 c。
具體實例
A 有一條消息給節點 D
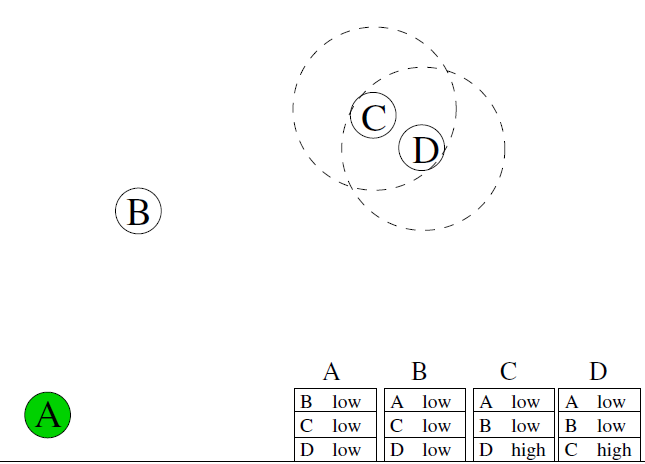
P(A,D)<P(B,D)P(A,D) < P(B,D)P(A,D)<P(B,D)所以A發給D
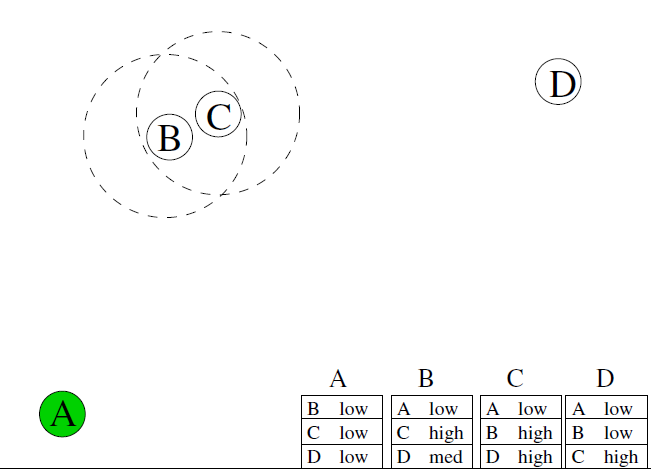
P(B,D)<P(C,D)P(B,D) < P(C,D)P(B,D)<P(C,D)所以B發給C
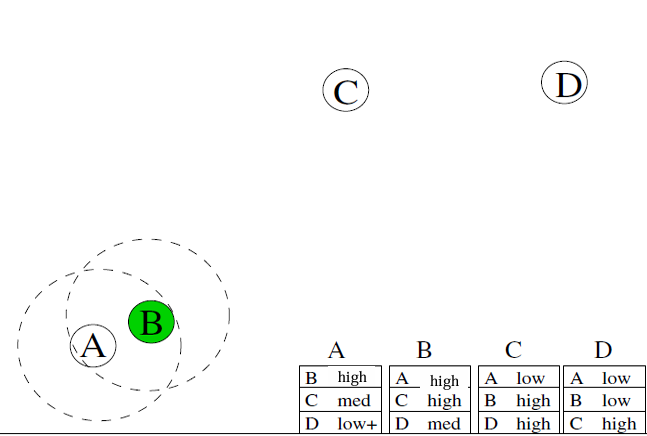
C 發給D,完成
實戰二——圖像邊界擴展cv2.copyMakeBorder())













-地形可視化處理)
 的優雅之道》)



-損失函數)