LeetCode 簡單JS刷題

返回數組最后一個元素

2787.將一個數字表示成冪的和的方案數

326.3的冪

1780.判斷一個數字是否可以表示成三的冪的和

342.4的冪

返回數組最后一個元素

1.請你編寫一段代碼實現一個數組方法，使任何數組都可以調用?array.last()?方法，這個方法將返回數組最后一個元素。如果數組中沒有元素，則返回?-1?。

你可以假設數組是?JSON.parse?的輸出結果。

示例 1 ：

輸入：nums = [null, {}, 3]
輸出：3
解釋：調用 nums.last() 后返回最后一個元素： 3。

示例 2 ：

輸入：nums = []
輸出：-1
解釋：因為此數組沒有元素，所以應該返回 -1。

提示：

arr?是一個有效的 JSON 數組
0 <= arr.length <= 1000

Array.prototype.last = function() {return this.length ? this.at(-1) : -1
};// at支持負索引，-1表示倒數第一個位置，-2則是倒數第二，以此類推

Array.prototype.last = function() {return this.length ? this.[this.length-1] : -1
};

2787.將一個數字表示成冪的和的方案數

2787. 將一個數字表示成冪的和的方案數

提示

給你兩個?正?整數?n?和?x?。

請你返回將?n?表示成一些?互不相同?正整數的?x?次冪之和的方案數。換句話說，你需要返回互不相同整數?[n1, n2, ..., nk]?的集合數目，滿足?n = n1x + n2x + ... + nkx?。

由于答案可能非常大，請你將它對?109 + 7?取余后返回。

比方說，n = 160?且?x = 3?，一個表示?n?的方法是?n = 23 + 33 + 53?。

示例 1：

輸入：n = 10, x = 2
輸出：1
解釋：我們可以將 n 表示為：n = 32 + 12 = 10 。
這是唯一將 10 表達成不同整數 2 次方之和的方案。

示例 2：

輸入：n = 4, x = 1
輸出：2
解釋：我們可以將 n 按以下方案表示：
- n = 41 = 4 。
- n = 31 + 11 = 4 。

提示：

1 <= n <= 300
1 <= x <= 5

var numberOfWays = function (n, x) {const MOD = Math.pow(10,9)+7const current = []// 獲取以x為冪的數組，大小不超過nfor(let i=1;i<=n;i++){current[i]=Math.pow(i,x)}// 創建一個長度為n+1，初始為0的數組const dp = new Array(n+1).fill(0)dp[0]=1// 核心代碼for(num of current){for(let k=n;k>=num;k--){dp[k]=(dp[k-num]+dp[k])%MOD}}return dp[n]
};

理解：這是一個01背包問題，我們先回顧一下01背包問題的初始形態是什么樣子的，即有一個最大承重為 W 的背包，有價格為v，重量為w的商品一堆，需要在不超過最大承重的前提下完成所選商品最貴的問題。我們可以用二維數組和一維數組來解決這個問題，關鍵在于，我放了和不放哪個會比較大？

二維數組：

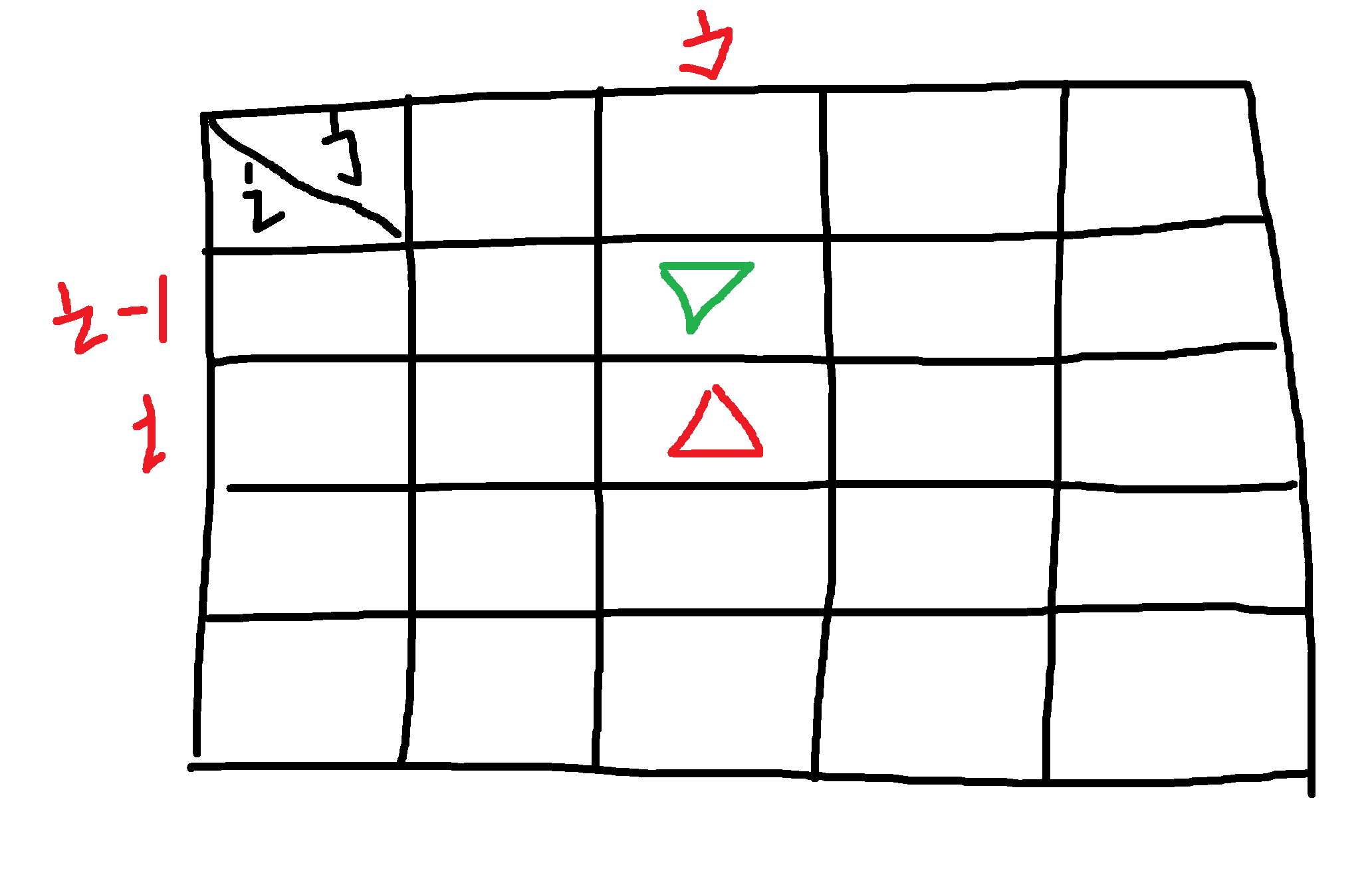
此時我的背包中的物品裝到了dp[i][j]的紅色三角形位置，此時我有倆個選項，

一是、我不把v[i]和w[i]的商品放進去，也就是dp[i-1][j]的綠色三角形位置，這么理解這個綠色三角形的位置吧，i-1 是上一個價格的所有狀態，dp[i-1][j] 可以被理解成再上一個價格在 j 重量時候的狀態；

二是、然后就是我放商品進去dp[i-1][j-w[i]]+v[i]? ,可以這么理解dp[i-1][j-w[i]]，把上一次狀態調到剛好可以放下這個新商品的體積，這個時候的重量應該是目前狀態的重量-新商品的體積對吧，也就是j-w[i],然后在這個狀態上加上新商品的價格。

for(let i=1;i<=V;i++){for(let j=1;j<=W;j++){if(j>w[i]){dp[i][j] = Max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])}}
}

一維數組：

其實由二維數組可以發現一個點，就是你的重量必須是要按順序從小增到大的，也就是 j 既是索引，又代表了實際重量，那么一維數組中索引代表重量不就行了嗎，然后具體數值是價格

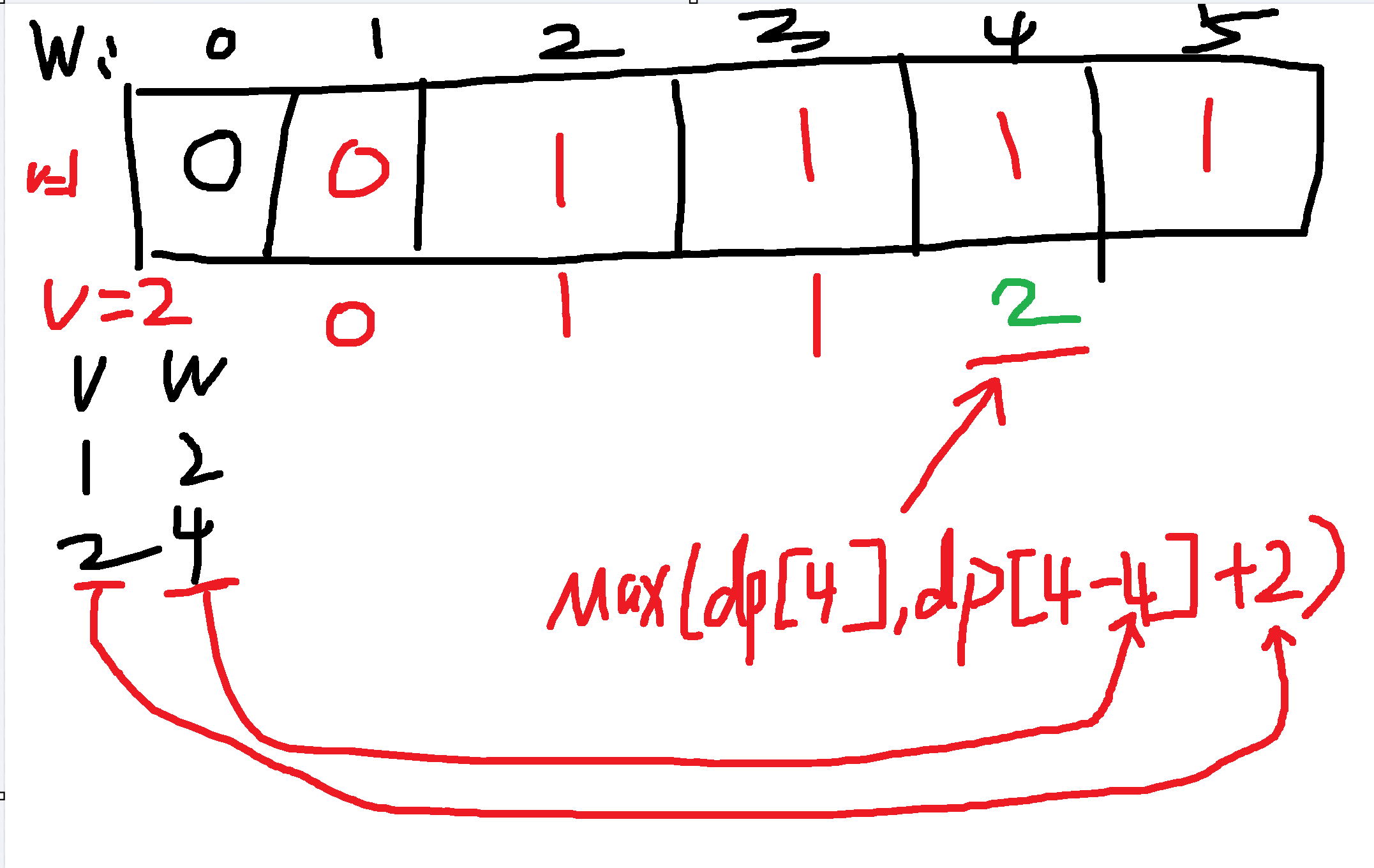
注意我下面寫的max(dp[i],dp[i-w[i]]+v[i]) 這個是基于v=1的時候的dp

OK，現在我們類比到這一題上面來

這里的n是不是就相當于是最大重量，由x次冪組成的數組[num1,num2,num3...],不就代表了索引和實際值相同的重量嗎

舉個例子 n=10 x=2

	0	1	2	4	9
0	1
1
2
3		dp[3]+dp[3-1]
...		dp[...]+dp[...-1]
10		dp[10]+dp[10-1]	dp[10]+dp[10-2]

上面的表格出來是不是就能看懂了，兩層循環，先遍歷n，然后里面嵌套是實現放不放num數組里的值，而且為什么這里不是用max比較大小呢？是因為無論我放不放都是一種方案，只要結果是實現了和等于n，所以應該是放和不放的情況加起來，用大白話理解就是，我有一系列的商品，我只是為了湊單，不管我放不放這一件它都是一種方案。

326.3的冪

326. 3 的冪

給定一個整數，寫一個函數來判斷它是否是 3?的冪次方。如果是，返回?true?；否則，返回?false?。

整數?n?是 3 的冪次方需滿足：存在整數?x?使得?n ==?

示例 1：

輸入：n = 27
輸出：true

示例 2：

輸入：n = 0
輸出：false

示例 3：

輸入：n = 9
輸出：true

示例 4：

輸入：n = 45
輸出：false

提示：

-?<= n <= ?- 1

進階：你能不使用循環或者遞歸來完成本題嗎？

// 循環
var isPowerOfThree = function(n) {let flag = nwhile(flag>=1){if(flag===1){return true;break}flag=flag/3     }return false
};

// 不循環
var isPowerOfThree = function(n) {return n>0 && Math.pow(3,19)%n===0 ?true:false
};

題解：循環的做法就是不斷除3，一直到等于1就返回true，不等于1就為false；不循環的做法就是取模，設置一個最大的3的冪（n<3的19次冪），然后對n取模，如果取出來為0就說明是3的冪,為什么呢？因為3是質數，大家都知道質數只能被1和自身整除，所以在一個不斷取模的過程中不會有其他數字干擾，舉個例子：4不是質數吧，如果我們要判斷一個數是否為4的冪，再用這個取模方法就不行了，假如用 $4^{2}$ ?對2和4分別取模，是不是得出來的結果都是0？但是2不是4的冪對吧，所以取模判斷這個方法只能對質數使用。

1780.判斷一個數字是否可以表示成三的冪的和

1780. 判斷一個數字是否可以表示成三的冪的和

給你一個整數?n?，如果你可以將?n?表示成若干個不同的三的冪之和，請你返回?true?，否則請返回?false?。

對于一個整數?y?，如果存在整數?x?滿足?y == 3x?，我們稱這個整數?y?是三的冪。

var checkPowersOfThree = function (n) {// n沒有除到底就繼續循環while(n>1){if(n%3===1){n=(n-1)/3}else if(n%3===0){n=n/3}else{// 除不出來說明不能展開為3的冪的和return false}}return true
};

題解：

大家看到這題會不會想到之前寫的那個背包問題？用01背包也能做，不過有倆個嵌套循環大大降低了代碼效率，而且會超時；

大家可以觀察一下，不知道大家的數學老師有沒有告訴過大家一個小技巧，如果有一個超大的數，判斷是否能被三整除，只需要把這個數的每一位拆分開，然后相加，這個時候數字是不是小了很多，我們就能判斷是否能被3整除了，例如：1233219這個數，拆分：1+2+3+3+2+1+9=21 =>2+1=3; 是不是說明1233219可以被3整除；

題目中說了，都是3的冪，且不同，那么我們可以這么做，我每次都除3，是不是剩下來的數不是余1，就是剛好除完？ok，可能有點抽象，我們來舉一個例子：

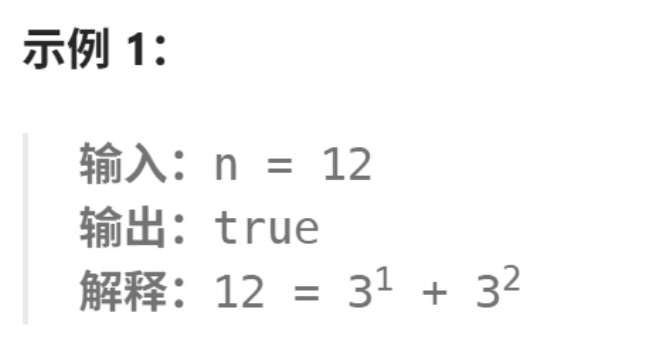
$12=$ $3^{1}+3^{2}$ ?對吧，那么現在我們對這個數除3，也就變成了 $3^{0}+3^{1}$ 是不是余1，然后我們-1繼續除3， $0+$ $3^{0}$ ,剛好為0，我猜你想知道為什么會這樣，題目有前提，每個都是3的冪，且不相同，那么我對一個全是3的冪除3，是不是每個數還是不同，只要我一直除下去，能除的盡，是不是就能說明n是可以被展開為不同的3的冪的和

342.4的冪

342. 4的冪

給定一個整數，寫一個函數來判斷它是否是 4 的冪次方。如果是，返回?true?；否則，返回?false?。

整數?n?是 4 的冪次方需滿足：存在整數?x?使得?n ==?

/*** @param {number} n* @return {boolean}*/
var isPowerOfFour = function(n) {while(n>=1){if(n===1){return true}n=n/4}return false
};

/*** @param {number} n* @return {boolean}*/
var isPowerOfFour = function(n) {return n>0 && n%3===1 && Math.pow(2,31)%n===0?true:false
};

題解：

這題大家是不是很眼熟，前面我們也寫了關于判斷是否為3的冪,最直接的判斷還是直接除啊，一直除到底；

另一種不需要循環的，我們知道，如果一個數是4的冪的話，肯定也是2的冪，所以我們可以縮小范圍去做，于是就有了

Math.pow(2,31)%n===0

大家都知道二項式定理：

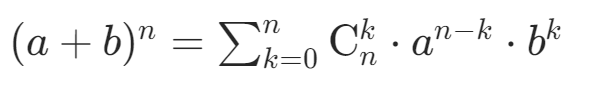
這里可以拆分成： $(3+1)^n$ ?,? $\sum_{k=0}^{n}$ ?? $_{n}^{k}\textrm{C}$ ? $3^{n-k}$

是不是變成了模3

。。。持續更新