目錄
一.排序的概念
二.常見排序算法的實現
2.1?插入排序
??(1)直接插入排序:
? 當插入第i(i>=1)個元素時,前面的array[0],array[1],…,array[i-1]已經排好序,此時用array[i]的排序碼與array[i-1],array[i-2],…的排序碼順序進行比較,找到插入位置即將array[i]插入,原來位置上的元素順序后移!
(2)希爾排序:
2.2選擇排序
?(1)?直接選擇排序:
(2)堆排序
2.3交換排序
(1)冒泡排序
(2)快速排序
? a.挖坑法
?思路:先取出最左側數據,保存在臨時變量key中(作為基準值),此時最左側由于數據被取走,所以此時就像一個坑位,下標用pivot表示,然后我們定義出begin和end變量,分別位于數組的左右兩側,end從右往左走,如果遇到比key值小的,就將該數據填入到坑位(num【pivot】)中,然后這里就變成了新的坑位,坑位以右的全是比key值大的;這時候begin向右走,遇到比key值大的就停下,將這個值填入到剛才的坑位中,以后就這樣循環,end走完begin走,每次走完都要更新坑位,直到begin和end相遇為止;
3.begin往右走的時候遇到了大于key的值停下來了,end往左走的時候沒有遇到小于key的,一直走到了begin:
? 對于這種情況,begin停下來后必然進行了一次坑位更新,此時begin就是一個沒有數據的坑位,當end到達坑位后,說明坑位右側必然是全都大于key,左側必然全都小于key,所以,我們應該將key保存在這個坑位處;
b.左右指針法
?編輯
?思路:和挖坑法有相似處,也是選取最左側為基準值key,定義begin和end在左右兩側,end在向左走的時候遇到小于key的就停下,begin向右走的時候遇到大于key的也停下,雙方此時交換一下元素,然后繼續重復上述過程,直到相遇;
代碼實現:
c.前后指針法
d.快速排序的非遞歸實現
2.4.歸并排序
遞歸實現??
非遞歸實現
三.排序算法復雜度及穩定性分析
一.排序的概念
? 1. 排序:所謂排序,就是使一串記錄,按照其中的某個或某些關鍵字的大小,遞增或遞減的排列起來的操作。
? 2.穩定性:假定在待排序的記錄序列中,存在多個具有相同的關鍵字的記錄,若經過排序,這些記錄的相對次序保持不變,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,則稱這種排序算法是穩定的;否則稱為不穩定的。
? 3.內部排序:數據元素全部放在內存中的排序。
? 4.外部排序:數據元素太多不能同時放在內存中,根據排序過程的要求不能在內外存之間移動數據的排序。
二.常見排序算法的實現
??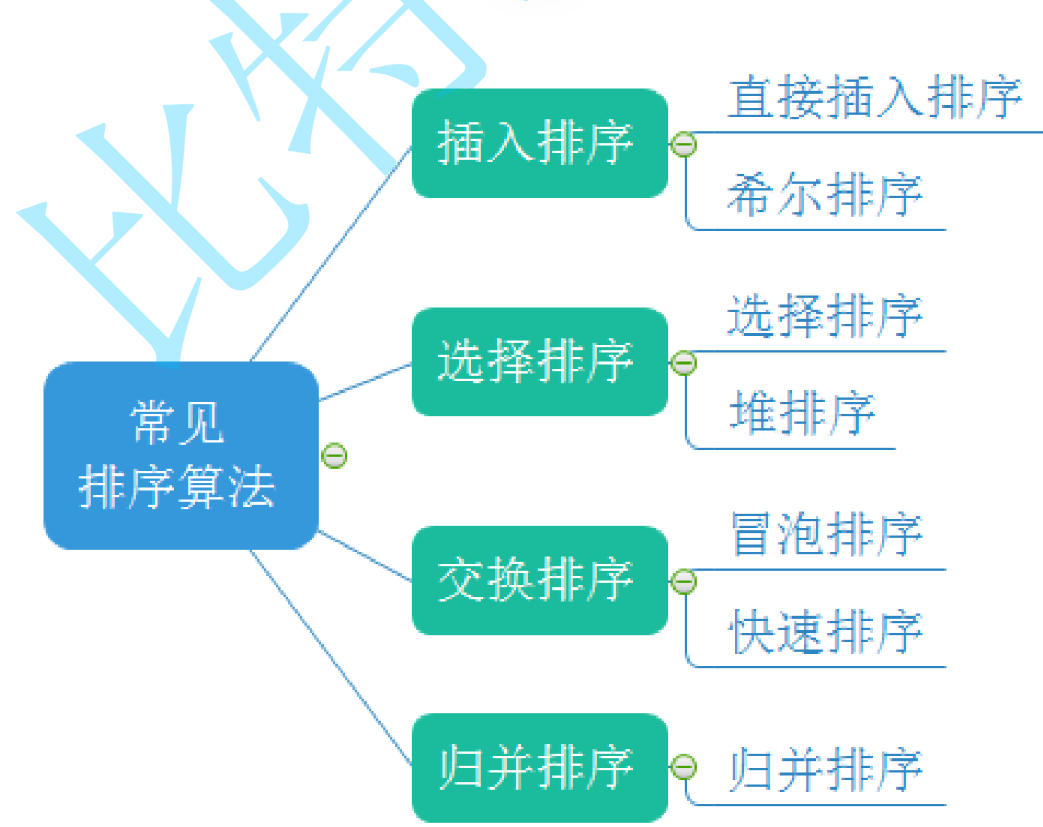
2.1?插入排序
??基本思想:把待排序的記錄按其關鍵碼值的大小逐個插入到一個已經排好序的有序序列中,直到所有的記錄插入完為止,得到一個新的有序序列?。
??(1)直接插入排序:
? 當插入第i(i>=1)個元素時,前面的array[0],array[1],…,array[i-1]已經排好序,此時用array[i]的排序碼與array[i-1],array[i-2],…的排序碼順序進行比較,找到插入位置即將array[i]插入,原來位置上的元素順序后移!
代碼實現:
void insertSort(int* num, int n)
{for (int i = 0; i < n - 1 ; i++){int end = i;int tmp = num[end + 1];for (end = i; end >= 0; end--){if (num[end] > tmp){num[end + 1] = num[end];}else{break;}}num[end + 1] = tmp;}}直接插入排序的特性總結:
? 1.?元素集合越接近有序,直接插入排序算法的時間效率越高
? 2.?時間復雜度:O(N^2)? ?
? 3.?空間復雜度:O(1),它是一種穩定的排序算法
? 4.?穩定性:穩定
(2)希爾排序:
? 基本思想是:先選定一個整數gap,把待排序文件中所有記錄分成幾個組,所有距離為gap的記錄分在同一組內,并對每一組內的記錄進行排序。然后gap縮小,重復上述分組和排序的工作。當gap到達=1時,所有記錄在統一組內排好序。
圖解: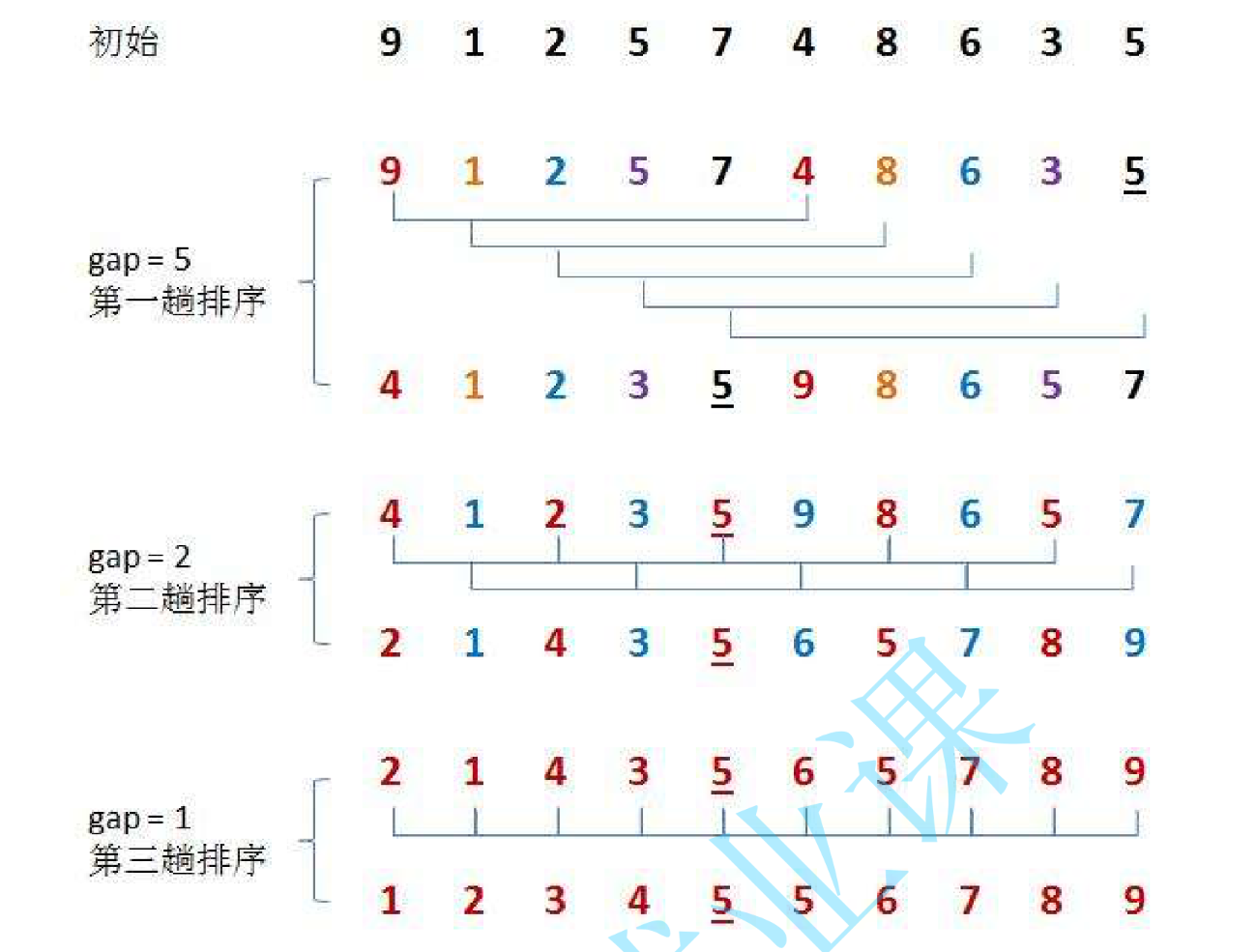
希爾排序的特性總結:
1.?希爾排序是對直接插入排序的優化。
2.?當gap?>?1時都是預排序(有間隔的插入排序),目的是讓數組更接近于有序。當gap?==?1時,就相當于直接插入排序,此時數組已經接近有序的了,這樣就會很快。這樣整體而言,可以達到優化的效果。
3.穩定性:不穩定
代碼實現:
void shellSort(int* num, int n)
{int gap = n/2;while (gap >= 1){for (int i = 0; i < n - gap; i ++){int end = i;int tmp = num[end + gap];while (end >= 0){if (num[end] > tmp){num[end + gap] = num[end];end -= gap;}else break;}num[end + gap] = tmp;}gap /= 2;}}2.2選擇排序
??基本思想:每一次從待排序的數據元素中選出最小(或最大)的一個元素,存放在序列的起始位置,直到全部待排序的數據元素排完?。
?(1)?直接選擇排序:
? ? 在元素集合array[i]--array[n-1]中選擇關鍵碼最大(小)的數據元素,若它不是這組元素中的最后一個(第一個)元素,則將它與這組元素中的最后一個(第一個)元素交換,在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重復上述步驟,直到集合剩余1個元素。
代碼實現:
void selectSort(int* num, int n)
{for (int begin = 0, end = n - 1; begin < end; begin++, end--){int max_id = begin, min_id = begin;for (int i = begin; i <= end; i++){if (num[i] > num[max_id]){max_id = i;}if (num[i] < num[min_id]){min_id = i;}}swap(num[begin], num[min_id]);if (max_id == begin){max_id = min_id;}swap(num[end], num[max_id]);}
}直接選擇排序的特性總結:
??1.?直接選擇排序思考非常好理解,但是效率不是很好。實際中很少使用
??2.?時間復雜度:O(N^2)
??3.?空間復雜度:O(1)
??4.?穩定性:不穩定
(2)堆排序
??堆排序(Heapsort)是指利用堆積樹(堆)這種數據結構所設計的一種排序算法,它是選擇排序的一種。它是通過堆來進行選擇數據。需要注意的是排升序要建大堆,排降序建小堆。
? 思路:先把數組構建成一個堆,然后依次取出堆頂元素,與數組末尾元素交換,然后自堆頂向下調整;
? 代碼:
void adjustDown(int* num, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && num[child + 1] > num[child]){child++;}if (num[child] > num[parent]){swap(num[child], num[parent]);parent = child;child = 2 * parent + 1;}else{break;}}
}
void heapSort(int *num,int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; i--){adjustDown(num, n, i);}for (int end = n-1; end > 0; end--){swap(num[0], num[end]);adjustDown(num, end, 0);}
}
堆排序的特性總結:
1.?堆排序使用堆來選數,效率就高了很多。
2.?時間復雜度:O(N*logN)
3.?空間復雜度:O(1)
4.?穩定性:不穩定
2.3交換排序
? 基本思想:所謂交換,就是根據序列中兩個記錄鍵值的比較結果來對換這兩個記錄在序列中的位置,交換排序的特點是:將鍵值較大的記錄向序列的尾部移動,鍵值較小的記錄向序列的前部移動。
(1)冒泡排序
? 冒泡排序(假設是升序)就是從左往右對所有數據依次進行兩兩比較進行交換,最終將最大的數據交換到了最右邊,這個過程就像冒泡泡一樣,最大值就是一個泡泡,經過n-1次冒泡后,整個排序也就完成了!
? 代碼實現:
void bubbleSort(int* num, int n)
{for (int i = 0; i < n - 1; i++){int flag = 1;for (int j = 0; j < n - i - 1; j++){if (num[j] > num[j + 1]){flag = 0;swap(num[j], num[j + 1]);}}if (flag){break;}}
}?冒泡排序的特性總結:
??1.?冒泡排序是一種非常容易理解的排序
??2.?時間復雜度:O(N^2)?
??3.?空間復雜度:O(1)
??4.?穩定性:穩定
(2)快速排序
? 基本思想為:任取待排序元素序列中的某元素作為基準值,按照該排序碼將待排序集合分割成兩子序列,左子序列中所有元素均小于基準值,右子序列中所有元素均大于基準值,然后對左右子序列重復該過程,直到所有元素都排列在相應位置上為止。
??將區間按照基準值劃分為左右兩半部分的常見方式有:
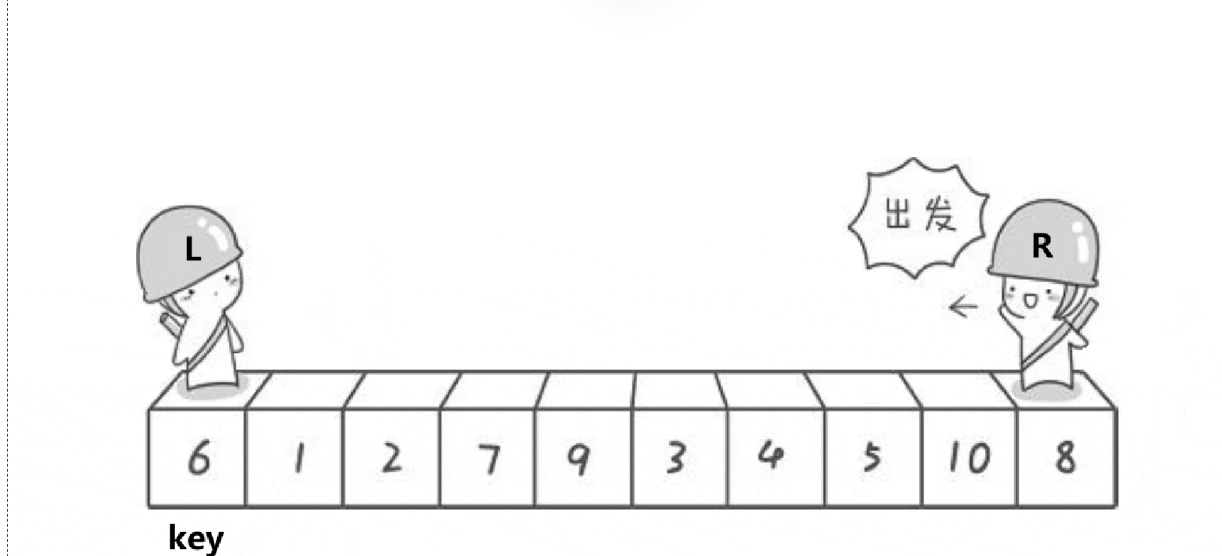
? a.挖坑法
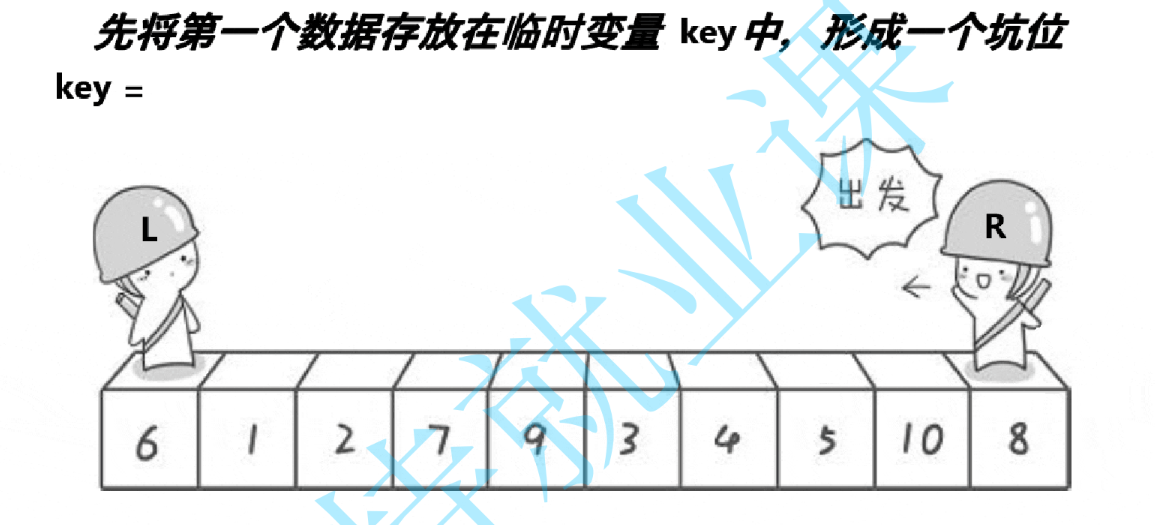
?思路:先取出最左側數據,保存在臨時變量key中(作為基準值),此時最左側由于數據被取走,所以此時就像一個坑位,下標用pivot表示,然后我們定義出begin和end變量,分別位于數組的左右兩側,end從右往左走,如果遇到比key值小的,就將該數據填入到坑位(num【pivot】)中,然后這里就變成了新的坑位,坑位以右的全是比key值大的;這時候begin向右走,遇到比key值大的就停下,將這個值填入到剛才的坑位中,以后就這樣循環,end走完begin走,每次走完都要更新坑位,直到begin和end相遇為止;
? 對于begin和end相遇,我們可以分析出以下幾種情況:
1.end剛開始在往左走的時候一直沒有遇到小于key的值,沒有停下來就走到了begin處:
? 這種情況其實就是數組已經有序了,最后begin和end都為0;基準值就該在最左側;
2.end遇到了小于key的值停下來后,begin沒有遇到大于key的值,一直走到了end處:
? 對于這種情況,end停下來后必然進行了一次坑位更新,此時end就是一個沒有數據的坑位,當begin到達坑位后,說明坑位左側必然是全都小于key,右側必然全都大于key,所以,我們應該將key保存在這個坑位處;
3.begin往右走的時候遇到了大于key的值停下來了,end往左走的時候沒有遇到小于key的,一直走到了begin:
? 對于這種情況,begin停下來后必然進行了一次坑位更新,此時begin就是一個沒有數據的坑位,當end到達坑位后,說明坑位右側必然是全都大于key,左側必然全都小于key,所以,我們應該將key保存在這個坑位處;
? 綜上三種情況,當begin與end相遇后,都會形成一個新的坑位,這個坑位就是key值應該在的位置,填入進去即可;
代碼實現:
??
void quickSort1(int* num, int left, int right)
{if (right <= left) return;int begin = left, end = right;int mid = (left + right) / 2;int id = Getmid(begin, end, mid);swap(num[id], num[begin]);int pivot = begin;int key = num[pivot];while (begin < end){while (begin < end && num[end] >= key){end--;}num[pivot] = num[end];pivot = end;while (begin < end && num[begin] <= key){begin++;}num[pivot] = num[begin];pivot = begin;}pivot = begin;num[pivot] = key;quickSort1(num, left, pivot - 1);quickSort1(num,pivot+1, right);
}b.左右指針法
?思路:和挖坑法有相似處,也是選取最左側為基準值key,定義begin和end在左右兩側,end在向左走的時候遇到小于key的就停下,begin向右走的時候遇到大于key的也停下,雙方此時交換一下元素,然后繼續重復上述過程,直到相遇;
此時的相遇也做一下情況討論:
1.剛開始end暢通無阻地到達了begin,即begin = end = 0,說明基準值就該在最左側;
2.end停下來后,begin一直走到了end處:
? end停下來的位置一定是小于key的,這個時候begin一直走到了end處,說明end左側全是小于key的,右側全是大于key的,只有腳下的數是小于key的;
3.begin停下來后,end一直走到了begin處:
? begin停下來后的位置元素一定是大于key的,而end所在的元素必然小于key,此時要和end所在的元素進行交換,這樣begin所在的元素就是小于key的了,這就導致接下來的end一直走到了begin處,說明begin左側全是小于key的,右側全是大于key的,只有腳下的數是于key的;
代碼實現:
void quickSort2(int* num, int left, int right)
{if (right <= left)return;int begin = left, end = right;int mid = (left + right) / 2;int id = Getmid(begin, end, mid);swap(num[id], num[begin]);int key = begin;while (begin < end){while (begin < end && num[end] >= num[key]){end--;}while (begin < end && num[begin] <= num[key]){begin++;}swap(num[begin], num[end]);}swap(num[key], num[begin]);quickSort2(num, left, begin - 1);quickSort2(num, begin+1, right);
}c.前后指針法

? 和前面兩種方法不同,這里定義prev和cur,分別位于首元素和第二元素處;這里是想要將數據從第二位置處開始記錄,cur從左往右走,只要遇到小于key的元素,就讓prev++,然后交換num[prev]和num[cur],這樣,cur走完以后,prev以及prev左側的數據全都是小于key的了,這時將key與num[prev]交換即可;
? 代碼實現:
void quickSort3(int* num, int left, int right)
{if (right <= left)return;int prev = commonPart(num, left, right);int begin = left, end = right;int mid = (left + right) / 2;int id = Getmid(begin, end, mid);swap(num[id], num[begin]);int key = begin;int prev = left, cur = left + 1;while (cur <= right){if (num[cur] < num[key] && cur != ++prev){swap(num[prev], num[cur]);}cur++;}swap(num[key], num[prev]);quickSort3(num, left, prev - 1);quickSort3(num, prev+1, right);
}d.快速排序的非遞歸實現
? 我們之前的做法都是讓基準值回到應該在的位置后,然后選出左右區間來遞歸執行;
? 如果要用非遞歸的方式,就要借助棧來實現,先將數組的左右端點入棧,注意入棧順序是右端點、左端點,因為棧的后進先出特性,先拿出的是左端點;
? 然后,出棧兩次就能拿到要操作區間的左右端點,進行基準值的定位后,將新的右區間入棧,左區間入棧,如果區間長度小于等于1就不入棧;這樣,只要棧不為空,我們就可以像遞歸方式一樣
進行每個區間的基準值定位了;
? 代碼實現:
int commonPart(int* num, int left, int right)
{int begin = left, end = right;int mid = (left + right) / 2;int id = Getmid(begin, end, mid);swap(num[id], num[begin]);int key = begin;int prev = left, cur = left + 1;while (cur <= right){if (num[cur] < num[key] && cur != ++prev){swap(num[prev], num[cur]);}cur++;}swap(num[key], num[prev]);return prev;
}void quickSort4(int* num, int left, int right)
{stack<int> st;st.push(right);st.push(left);while (!st.empty()){int begin = st.top(); st.pop();int end = st.top(); st.pop();int prev = commonPart(num, begin, end);if (prev + 1 < end){st.push(end);st.push(prev + 1);}if (begin < prev-1 ){st.push(prev - 1);st.push(begin);}}
}快排最壞情況的兩種典型場景(On2)
??1.數組已經有序(升序或降序)
??當輸入數組已經有序時,如果每次選擇第一個或最后一個元素作為基準值,每次分區只能減少一個元素。例如:對于數組[1,?2,?3,?4,?5],選擇第一個元素1作為基準值,分區后左邊為空,右邊為[2,?3,?4,?5]遞歸樹會退化為鏈表,深度為n,總比較次數為n?+?(n-1)?+?(n-2)?+?…?+?1?=?n(n+1)/2
??2.所有元素相同
當數組中所有元素都相等時,如果分區策略不當,也會導致極度不均衡的分區
例如:數組[5,?5,?5,?5,?5],如果基準值選擇和分區實現不當,可能導致每次只減少一個元素
可以通過合理選擇基準值來規避這種風險
?快速排序優化
1.?三數取中法選key
? 三數取中法的核心思想是從待排序數組中選擇三個元素,通常是首元素、中間元素和末元素,然后取這三個元素的中位數作為基準值(pivot)。這種方法可以有效避免在數組已經有序或接近有序時出現的最壞情況。
代碼實現:
int Getmid(int x, int y, int k)
{int max = x, min = x;if (y > x) max = y;if (k > x) max = k;if (y < min) min = y;if (k < min) min = k;return x + y + k - max - min;
}2.?遞歸到小的子區間時,可以考慮使用插入排序??
快速排序的特性總結:
1.?快速排序整體的綜合性能和使用場景都是比較好的,所以才敢叫快速排序
2.?時間復雜度:O(N*logN)
3.?空間復雜度:O(logN)
4.?穩定性:不穩定
2.4.歸并排序
基本思想:
??歸并排序是建立在歸并操作上的一種有效的排序算法,該算法是采用分治法的一個非常典型的應用。將已有序的子序列合并,得到完全有序的序列;即先使每個子序列有序,再使子序列段間有序。若將兩個有序表合并成一個有序表,稱為二路歸并。?歸并排序核心步驟:
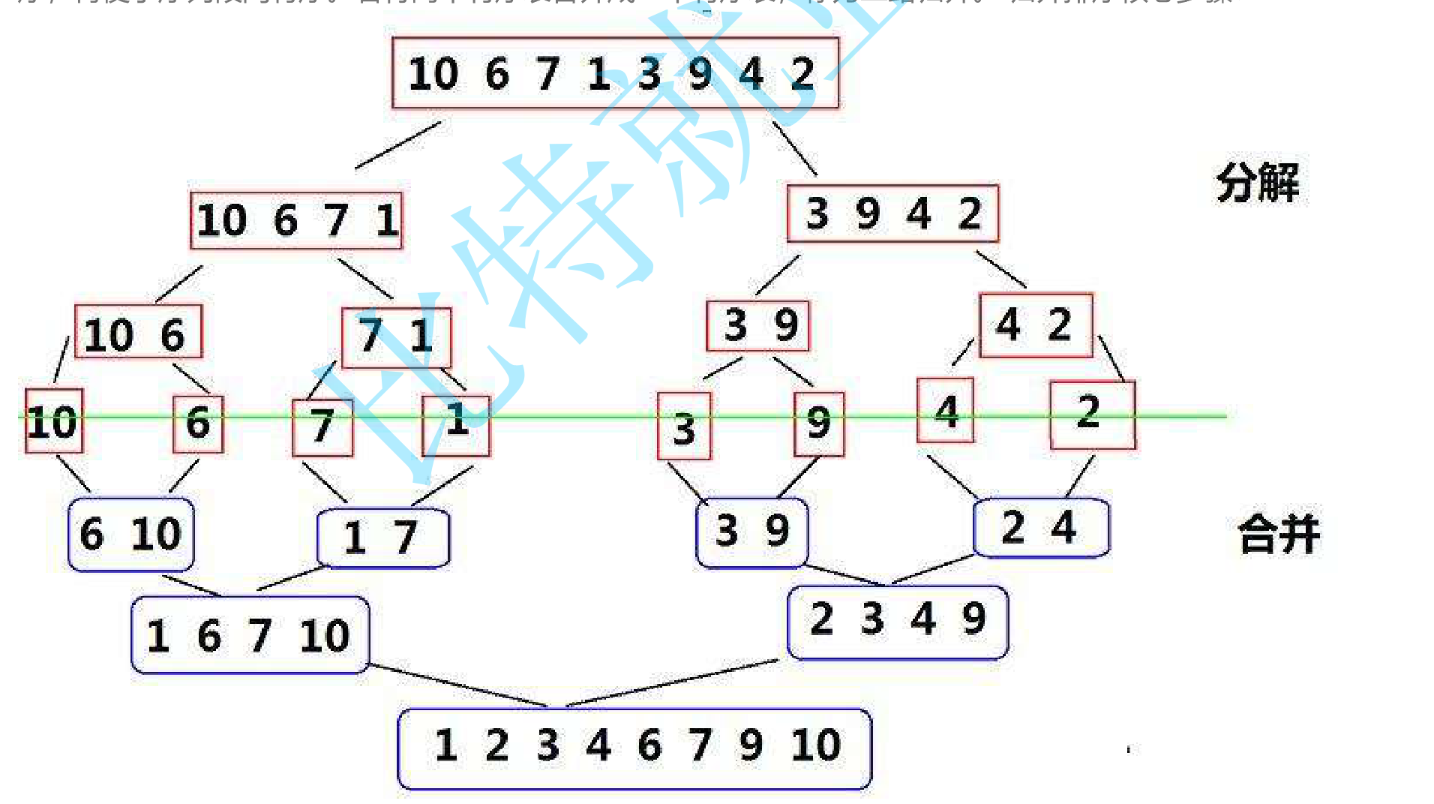
遞歸實現??
歸并排序說到底就是合并兩個有序的序列,但是我們如何將數組變成兩個有序序列呢?可以采用找中間下標,分成左右區間分別遞歸的方式,遞歸到最后就是兩個元素的區間排序,一個元素肯定是有序序列了,因此此時可以做合并,從下往上回調,最后整個數組就會變成有序序列了!
? 代碼實現:
void MergeSort(int* num, int left, int right, int* tmp)
{if (right <= left)return;int mid = (left + right) / 2;int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;MergeSort(num, begin1, end1, tmp);MergeSort(num, begin2, end2, tmp);int index = left;while (begin1 <= end1 && begin2 <= end2){if (num[begin1] < num[begin2]){tmp[index++] = num[begin1++];}else{tmp[index++] = num[begin2++];}}while (begin1 <= end1){tmp[index++] = num[begin1++];}while (begin2 <= end2){tmp[index++] = num[begin2++];}for (int i = left; i <= right; i++){num[i] = tmp[i];}}
void mergeSort1(int* num, int n)
{int* tmp = new int[n];MergeSort(num, 0, n - 1, tmp);
}非遞歸實現
? 再回憶一下歸并排序的思路,首先我們要將數組變成兩個有序序列,然后將他們合并起來即可;
關鍵點是怎么得到兩個有序序列,從遞歸的思路不難看出,我們是要從底層慢慢構建出有序序列的,即先進行區間大小為1的有序序列合并,這樣就獲得了大小為2的有序序列,再進行大小為2的有序序列合并,就得到了大小為4的有序序列……依次類推即可;
? 隨著要合并的有序序列區間的增大,難免會出現區間端點超出數組范圍的情況,下面分情況討論:
? 1.左區間的右端點超出范圍或右區間的左端點超出范圍,此時左區間內的數據已經有序了,因此無需合并;
? 2.右區間的左端點合法,但右端點超范圍,此時要將右端點改為數組的右端點,然后進行左右區間的合并;
代碼實現:
void _mergesort(int* num, int begin1, int end1, int begin2, int end2,int *tmp)
{int index = begin1;int left = begin1, right = end2;while (begin1 <= end1 && begin2 <= end2){if (num[begin1] < num[begin2]){tmp[index++] = num[begin1++];}else{tmp[index++] = num[begin2++];}}while (begin1 <= end1){tmp[index++] = num[begin1++];}while (begin2 <= end2){tmp[index++] = num[begin2++];}for (int i = left; i <= right; i++){num[i] = tmp[i];}
}
void mergeSort2(int* num, int n)
{int* tmp = new int[n];int gap = 1;while (gap < n) {for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;if (begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}_mergesort(num, begin1, end1, begin2, end2, tmp);}gap *= 2;}
}
歸并排序的特性總結:
1.?歸并的缺點在于需要O(N)的空間復雜度,歸并排序的思考更多的是解決在磁盤中的外排序問題。
2.?時間復雜度:O(N*logN)
3.?空間復雜度:O(N)
4.?穩定性:穩定
三.排序算法復雜度及穩定性分析
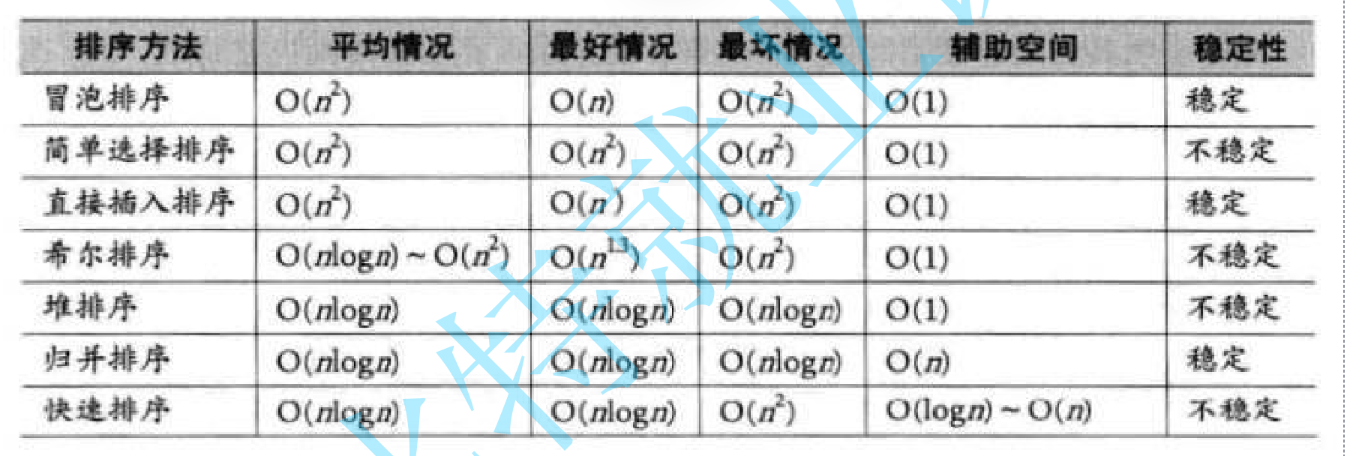











跳過登錄微軟賬戶,創建本地賬戶)







