Blender模擬結構光3D Scanner（一）外參數匹配

如何使用Blender模擬FPP(Fringe Projection Profilometry) 原理的結構光3D傳感器？

主要包含的工作有：

1）相機、投影儀定位與內外參數匹配；

2）投影儀投射指定Pattern圖像；

3）被測物體材質屬性配置等；

本篇主要關注外參數匹配。

外參數匹配的基本思路?是，添加Camera和SpotLight節點，并設置各自的變換（Transform）屬性，主要是位置 $X/Y/Z$ 和旋轉 $X/Y/Z$ 六個參數。

1 Blender中變換參數的含義

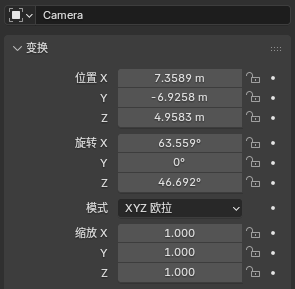
Blender中，變換參數的含義可理解為世界坐標系到當前Object坐標系的變換，用位置 $X/Y/Z$ 和旋轉 $X/Y/Z$ 可分別表示為 $\boldsymbol{T}_{3 \times 1}$ 和 $\boldsymbol{R}_{3 \times 3}$ 。

則Object坐標系下的點 $\boldsymbol{P}_\textnormal{obj}$ 與該點在世界坐標系下的坐標 $\boldsymbol{P}_\textnormal{W}$ 之間的變換關系為

$\boldsymbol{P}_\textnormal{obj}=\boldsymbol{R}\boldsymbol{P}_\textnormal{W}-\boldsymbol{R}\boldsymbol{T}$ ? (1-1)

2 左相機變換參數配置

在三維測量中慣用的相機坐標系定義為，

$X$ ?——? 相機畫幅平面內水平向右的方向為 $X$ 正方向；

$Y$ ?—— 相機畫幅平面內豎直向下的方向為 $Y$ 正方向；

$Z$ ?—— 相機觀測正前方（Front）方向為 $Z$ 正方向；

????????但Blender中，相機坐標系的定義是不同的。具體表現為，在Blender中將相機變換參數的位置 $X/Y/Z$ 和旋轉 $X/Y/Z$ 都設置為0，如圖1所示。

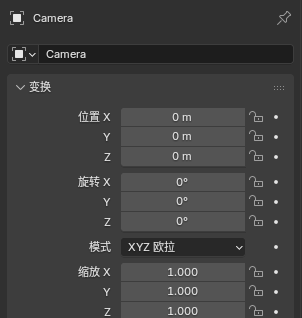
圖1 相機位置和旋轉參數置0

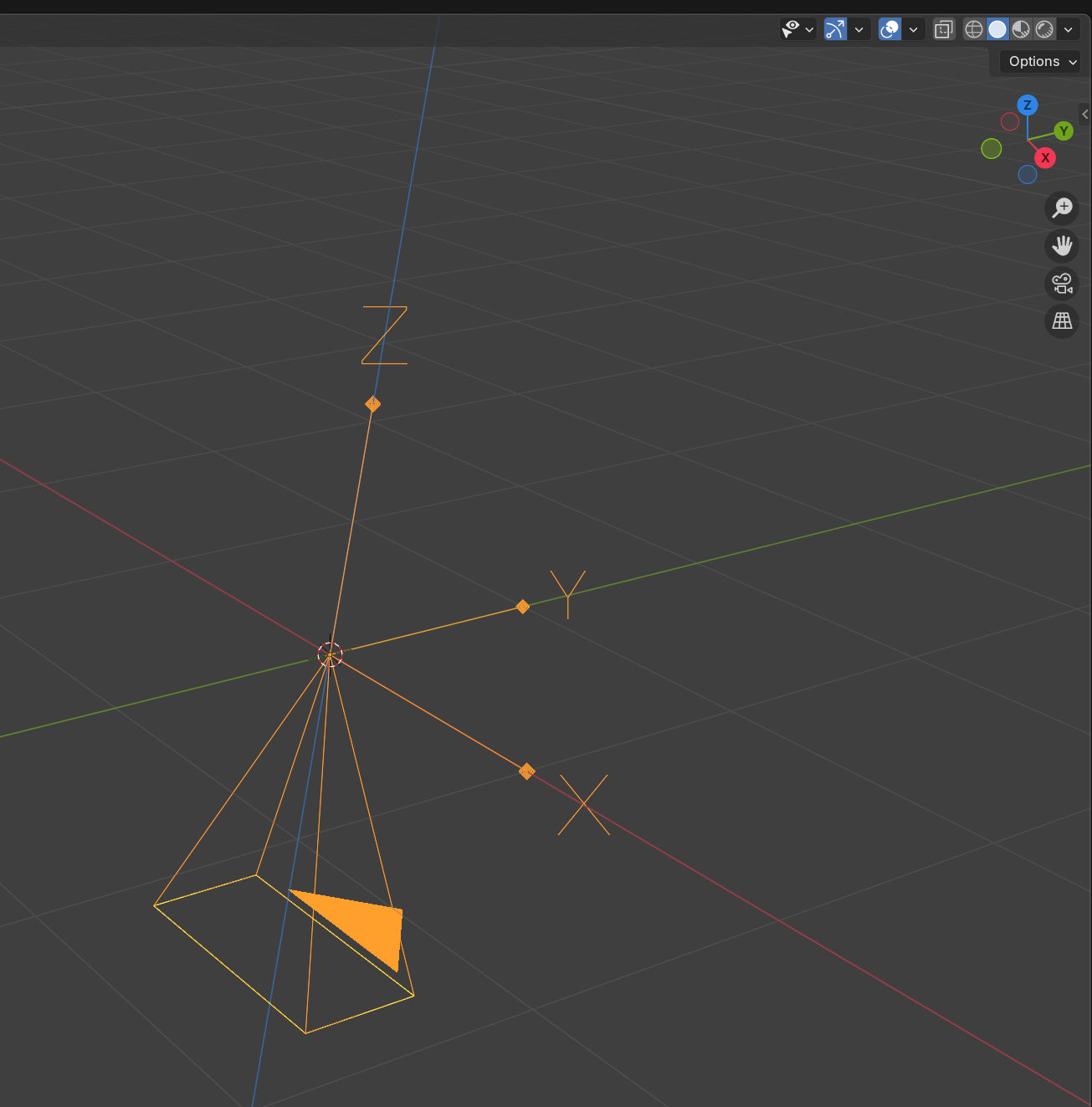
圖2 相機視野和方向

????????此時相機的視野和方向如圖2，圖中和紅色/綠色/藍色線為世界坐標系 $XYZ$ 三軸的軸線，三個軸的正方向可參見右上角的坐標軸縮略圖（彩色實心圓指向軸的正方向）；圖中橙色線段，端點標有 $XYZ$ 的是相機坐標系；相機的視野前方為世界坐標系的 $Z$ 負方向，相機視野的上方向為世界坐標系的 $Y$ 正方向。

? ? ? ? 為了使相機的視野前方與上方向與三維測量中慣用的相機相匹配，需要設置Blender中相機旋轉變換參數，旋轉 $Y/Z$ 軸均設置180°，如圖3所示。設置后，相機視野前方指向 $Z$ 正方向，視野上方指向 $Y$ 負方向。

? ? ? ? 但注意此時Blender中相機坐標系（橙色）的各軸方向為：????????

???????? $X$ ?——? 與世界坐標系 $X$ 正方向一致；

???????? $Y$ ?—— 與世界坐標系 $Y$ 正方向相反；

???????? $Z$ ?—— 與世界坐標系 $Z$ 正方向相反；

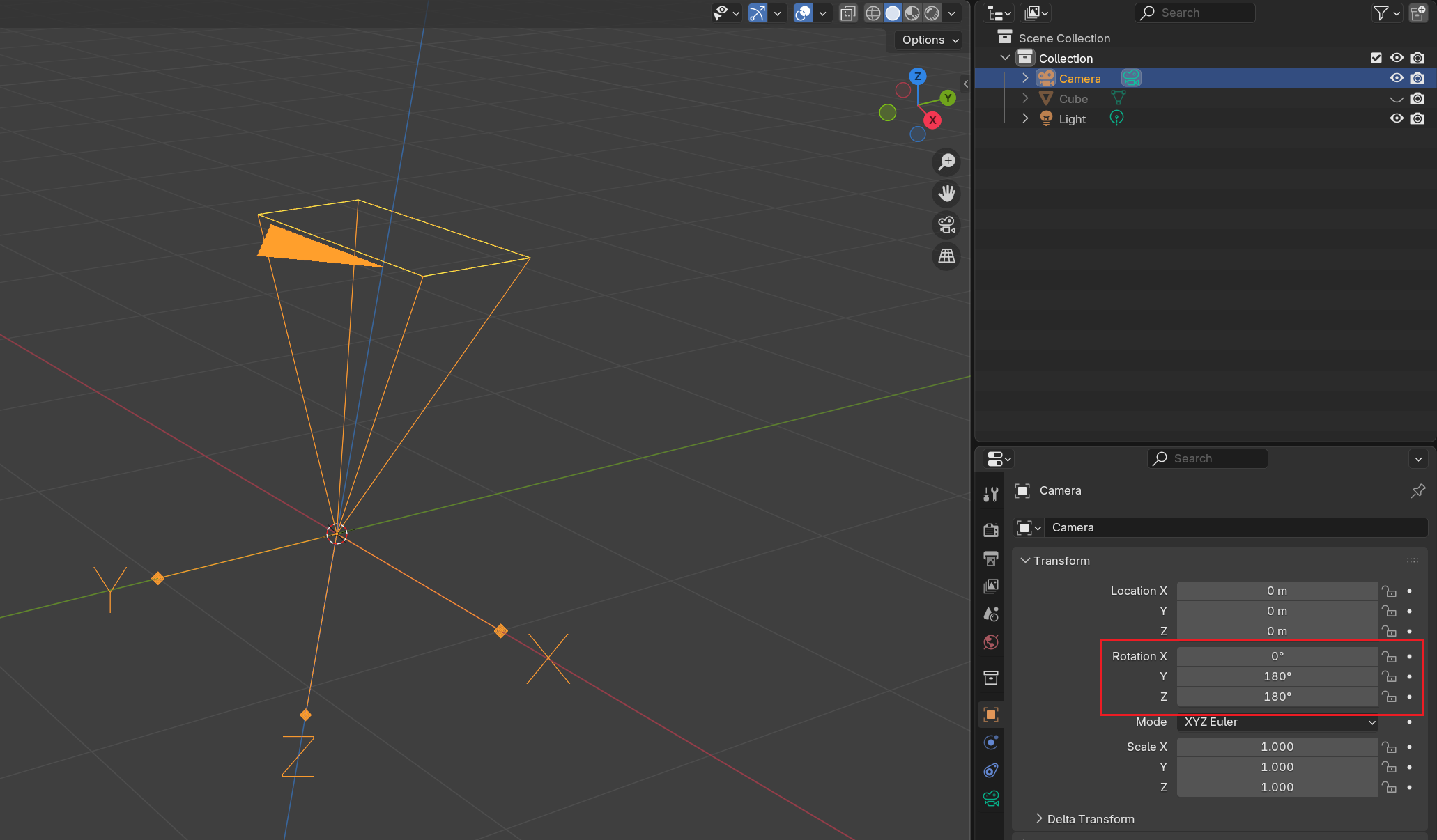
圖3 旋轉 $Y/Z$ 軸均設置180°后的Blender相機坐標系

? ? ? ? 根據式（1-1），此時Blender相機坐標系下點的坐標 $\boldsymbol{P}_{\textnormal{C}}$ 與該點在世界坐標系下的表示 $\boldsymbol{P}_{\textnormal{W}}$ 的關系為

$\boldsymbol{P}_{\textnormal{C}}=\boldsymbol{R}_{\textnormal{C}}\boldsymbol{P}_{\textnormal{W}}$ ?（2-1）

式中， $\boldsymbol{R}_{\textnormal{C}}$ 對應旋轉變換參數 $Y/Z$ 軸均設置180°。

? ? ? ? 但是，此時Blender相機坐標系和三維測量慣用的相機坐標系（本節開頭）定義仍是不同的，若在此時Blender相機節點的位置，建立三維測量慣用的相機坐標系，設該坐標系下點的坐標為 $\boldsymbol{P'}_\textnormal{C}$ ，則 $\boldsymbol{P'}_\textnormal{C}$ 與該點在Blender相機坐標系下的坐標 $\boldsymbol{P}_{\textnormal{C}}$ 之間的變換關系為

$\boldsymbol{P'}_\textnormal{C}=\boldsymbol{R}_x\boldsymbol{P}_\textnormal{c}$ ? （2-2）

????????式中， $\boldsymbol{R}_x$ 對應旋轉變換參數 $X$ 軸旋轉180°，即Blender相機坐標系繞 $X$ 軸旋轉180°可構造出三維測量慣用的相機坐標系。

3 投影儀變換參數配置

? ? ? ? 投影儀和雙目系統中右相機的地位是相同的。在Blender中可通過設置聚光燈（Spot Light）+圖像紋理的方式來模擬投影儀的效果。參考式（1-1）,配置投影儀變換參數即確定 $\boldsymbol{R}_\textnormal{P}$ 與 $\boldsymbol{T}_\textnormal{P}$

$\boldsymbol{P}_\textnormal{P}=\boldsymbol{R}_\textnormal{P}\boldsymbol{P}_\textnormal{W}-\boldsymbol{R}_\textnormal{P}\boldsymbol{T}_\textnormal{P}$ ? （3-1）

????????聚光燈的坐標系（即投影儀坐標系）與第2節中Blender相機坐標系的定義是類似的，也存在Blender投影儀坐標系與三維測量慣用的投影儀坐標系差距 $\boldsymbol{R}_x$ 旋轉的問題，即

$\boldsymbol{P'}_\textnormal{P}=\boldsymbol{R}_x\boldsymbol{P}_\textnormal{P}$ ?（3-2）

? ? ? ? 若三維測量系統標定外參數已知，即三維測量慣用的投影儀坐標系與三維測量慣用的左相機坐標系的變換關系已知，則有

$\boldsymbol{P'}_\textnormal{P}=\boldsymbol{R}\boldsymbol{P'}_\textnormal{C}+\boldsymbol{T}$ ?（3-3）

? ? ? ? 聯立式（2-1）、（2-2）、（3-1）、（3-2）、（3-3）可求得投影儀變換旋轉參數 $\boldsymbol{R}_\textnormal{P}$ 和平移參數 $\boldsymbol{T}_\textnormal{P}$ ，即可對應得到Blender聚光燈的變換參數。

$\boldsymbol{R}_x\boldsymbol{P}_\textnormal{P}=\boldsymbol{R}\boldsymbol{R}_x\boldsymbol{P}_\textnormal{c}+\boldsymbol{T}$

$\boldsymbol{R}_x(\boldsymbol{R}_\textnormal{P}\boldsymbol{P}_\textnormal{W}-\boldsymbol{R}_\textnormal{P}\boldsymbol{T}_\textnormal{P})=\boldsymbol{R}\boldsymbol{R}_x\boldsymbol{R}_\textnormal{C}\boldsymbol{P}_\textnormal{W}+\boldsymbol{T}$

$\boldsymbol{R}_x\boldsymbol{R}_\textnormal{P}\boldsymbol{P}_\textnormal{W}=\boldsymbol{R}\boldsymbol{R}_x\boldsymbol{R}_\textnormal{C}\boldsymbol{P}_\textnormal{W}$

$\boldsymbol{R}_\textnormal{P}=\boldsymbol{R}_x^{\top}\boldsymbol{R}\boldsymbol{R}_x\boldsymbol{R}_\textnormal{C}$ ??(3-4)

$-\boldsymbol{R}_x\boldsymbol{R}_\textnormal{P}\boldsymbol{T}_\textnormal{P}=\boldsymbol{T}$

$-\boldsymbol{R}_x\boldsymbol{R}_x^{\top}\boldsymbol{R}\boldsymbol{R}_x\boldsymbol{R}_\textnormal{C}\boldsymbol{T}_\textnormal{P}=\boldsymbol{T}$

$-\boldsymbol{R}\boldsymbol{R}_x\boldsymbol{R}_\textnormal{C}\boldsymbol{T}_\textnormal{P}=\boldsymbol{T}$

$\boldsymbol{T}_\textnormal{P}=-(\boldsymbol{R}\boldsymbol{R}_x\boldsymbol{R}_\textnormal{C})^{\top}\boldsymbol{T}$ ??(3-5)

注意，式中 $\boldsymbol{R}_x\boldsymbol{R}_\textnormal{C}$ 可理解為分別繞 $XYZ$ 三個軸各轉了180°，相當于沒有轉！

所以有

$\boldsymbol{T}_\textnormal{P}=-\boldsymbol{R}^{\top}\boldsymbol{T}$ ??(3-6)

最終實驗得到的一組投影儀變換參數和相機-投影儀位置關系如圖4所示

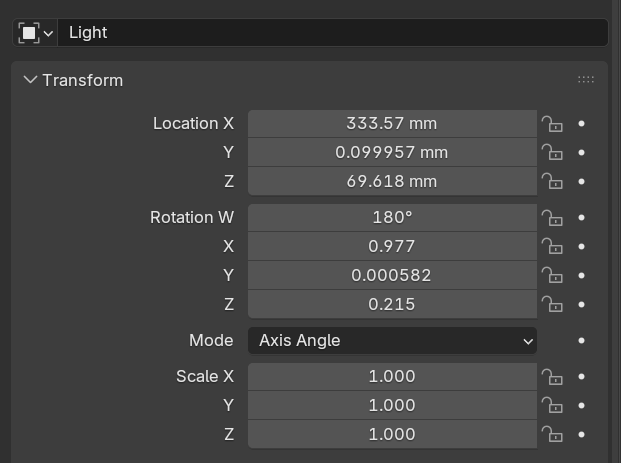
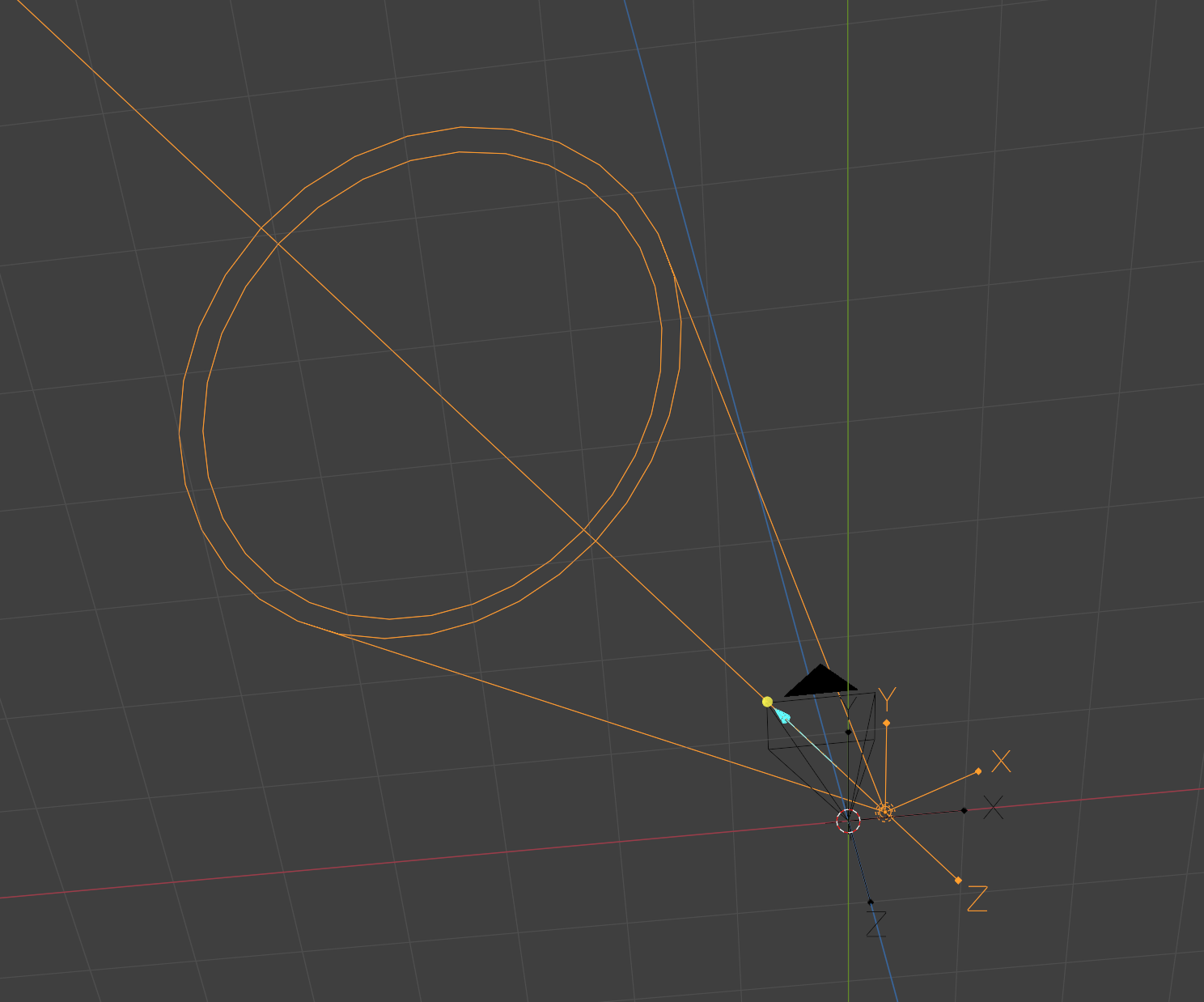
圖4?實驗得到的一組投影儀變換參數和相機-投影儀位置關系

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/918649.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/918649.shtml
英文地址，請注明出處：http://en.pswp.cn/news/918649.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！