目錄
簡介:
一、什么是支持向量機
二、如何選取最佳的超平面
1.超平面方程 (優化目標)
2.如何尋找最優的超平面
3.舉例分析
4.軟間隔?編輯
三、核函數
1舉例
2常用核函數
3.多項式核函數
4.高斯核函數:
四、svm的優缺點
五、支持向量機的API
六、案例分析
簡介:
????????歡迎來到機器學習系列課程的第七課!在這一課中,我們將聚焦于支持向量機(SVM) 這一經典且極具影響力的算法。作為監督學習領域的重要工具,SVM 憑借其出色的泛化能力和在小樣本、高維空間中的優異表現,至今仍被廣泛應用于圖像識別、文本分類、生物信息學等多個領域。本節將從 SVM 的基本原理講起,帶大家理解它如何通過尋找最優超平面來實現數據分類 —— 這一超平面不僅能將不同類別的樣本清晰分隔,還能使兩類樣本到超平面的最小距離(間隔)最大化,從而提升模型的穩定性。我們會深入剖析 “支持向量” 的核心概念,揭示這些關鍵樣本點如何決定超平面的位置,以及它們在模型訓練中的特殊作用。此外,面對線性不可分的數據,SVM 的核函數技巧堪稱 “點睛之筆”。我們將詳細解讀線性核、多項式核、徑向基核(RBF)等常用核函數的原理,展示它們如何將低維空間中線性不可分的數據映射到高維空間,進而實現線性可分。同時,還會探討正則化參數(C)對模型復雜度和泛化能力的影響,幫助大家掌握 SVM 的調優思路。
一、什么是支持向量機
????????很久以前的情人節,公主被魔鬼綁架了,王子要去救公主,魔鬼和他玩了一個游戲。魔鬼在桌子上似乎有規律放了兩種顏色的球,說:“你用一根棍分開它們?要求:盡量在放更多球之后,仍然適用。”

- 第一次,王子這么放:
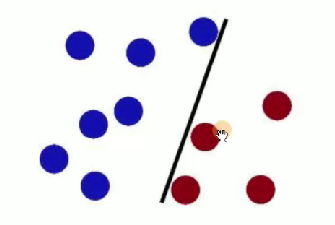
- 魔鬼又擺了更多的球,有一個球站錯了陣營:
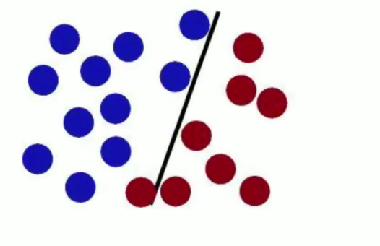
SVM 試圖把棍子放在最佳位置,使棍兩邊有盡可能大的間隙 。
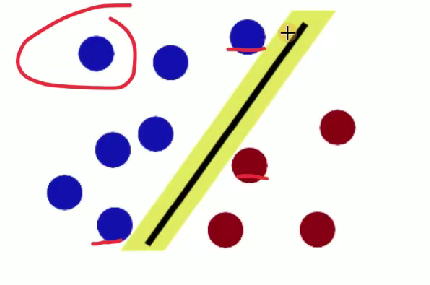
魔鬼放更多球后,棍仍能作為好的分界線 ,體現 SVM 對數據分類的有效性與泛化能力 。
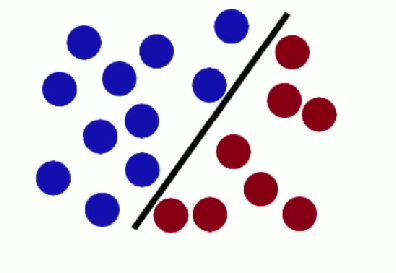
????????魔鬼使花招重新擺放球,王子拍桌讓球飛起,拿紙插在兩種顏色球中間 ,用于形象闡釋 SVM 處理線性不可分等情況時的核函數等思想(將低維線性不可分數據映射到高維實現線性可分,類似把球 “升維” 后用平面分隔 )。
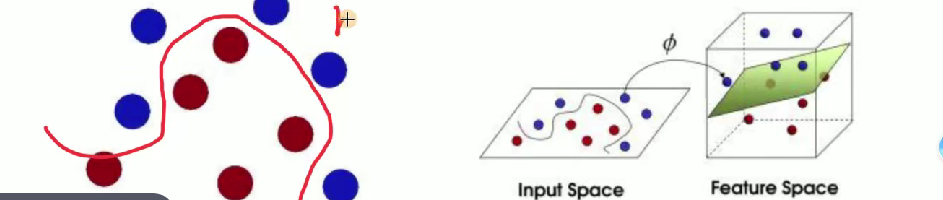
解釋 SVM(支持向量機)相關概念?
- 球 -> [data -> 數據]
- 棍子 -> [classifier -> 分類器]
- 最大間隙 trick -> [optimization -> 最優化]
- 拍桌子 -> [kernelling -> 核函數]
- 那張紙 -> [hyperplane -> 超平面]
二、如何選取最佳的超平面
對于這個圖片我們去尋找

1.超平面方程 (優化目標)
樣本點假設
假設有一堆樣本點
不同維度平面方程
- 二維平面:
- 常規直線方程:
- 轉化后的形式:
,備注 “一條線”
- 常規直線方程:
- 三維平面:
- 方程:
?,備注 “平面”
- 方程:
- 更高維平面(超平面):
- 方程:
,備注 “超平面”
- 方程:
綜合超平面函數
,右側備注 “
看作x”
標簽問題
????????在 SVM 中我們不用 0 和 1 來區分,使用 + 1 和 - 1 來區分,這樣會更嚴格。 假設超平面可以將訓練的樣本正確分類,那么對于任意樣本: 如果?,則稱為正例,
,則稱為負例。
決策函數:
符號函數
整合
決策函數
樣本點分類正確的情況
當樣本點分類正確的時候,有:
- 若?
,則?
(正例 )
- 若?
,則?
(負例 )
整合結果
距離問題:
(1)點到直線的距離
(2)點到平面的距離
(3)點到超平面的距離
????????簡寫為:,其中
是
的范數,
是樣本
的映射 。這是 SVM 中關于點到超平面距離的數學表達,用于后續優化間隔等操作 。
改進:
對公式加上正確性:
分類正確條件
分類正確時:
兩個衡量指標
- (1) 確信度:點到超平面距離
- (2) 正確性:分類正確
2.如何尋找最優的超平面
步驟(1):找到離超平面最近的點
步驟(2):最大化這個距離
使得離超平面最近的點到超平面的距離越遠越好。
最終構成損失函數求解
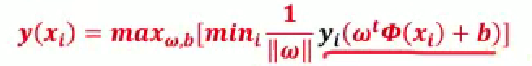
步驟(1):設定最小值
令?,右側原因說明:因分類正確時?
?,經放縮變換可使?
,讓條件更嚴格 。
步驟(2):轉化優化目標
則優化目標變為??且?
?,即要在滿足?
的約束下,最大化?
,等價于最小化?
,這是 SVM 損失函數求解及優化目標轉換的關鍵步驟 。
拉格朗日乘子法:
求解有約束條件的極值問題
- 函數:
- 約束條件:
對應 SVM 的目標與約束
修改目標函數與約束條件相關內容
原目標函數:
轉化后:
(極值點不變 )
經過一系列的操作得到
![]()
3.舉例分析
對于svm的推導公式實在晦澀難懂,我們直接講述一個案例就好理解了。已知如圖所示訓練數據集,求最大間隔分離超平面。
- 正例點:
,
- 負例點:
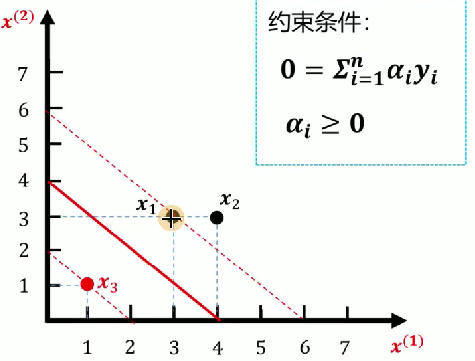
1.數據點代入公式
2.添加約束
- 等式約束:
?,推出?
- 不等式約束:
3.代入化簡
化簡后的式子:?,通過求最小值(求偏導方式)進一步處理 。
對和
求偏導等于 0
- 計算得
(滿足
)
(不滿足
?)
4.條件判斷
因不滿足條件,對應超平面方程不可取(強調先決條件必須滿足 )
5.思考
解不在偏導為 0 的位置,應在邊界上(或
等于 0 )
令或
等于 0
-
當
時: 代入原式得
?,求偏導后得
,再代入原式求最小值為
。
-
當
時: 代入原式得
,求偏導后得
,再代入原式求最小值為
。
????????最小值在處取得 ,這是 SVM 對偶問題求解中處理約束條件、尋找最優解的關鍵推導流程 。
6.求解每個
,由
,得
7.求解參數
8. 求解參數b
公式:
- <1> 帶入正例\(y = 1\),
:
- <2> 帶入負例\(y = -1\),
:
9.總方程
最后我們就求出svm的核函數為上圖中的那條紅線。
4.軟間隔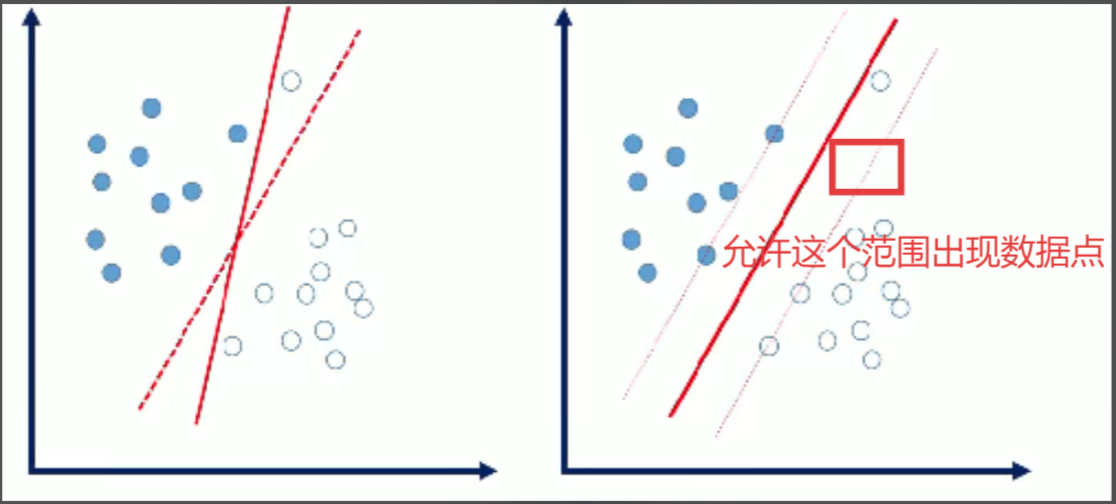
軟間隔:數據中存在一些噪音點,如果考慮這些噪音點的話,超平面可能表現的效果不好。
我們允許個別樣本點出現在間隔帶里面。
量化指標:引入松弛因子。
原始:?[每個樣本點必須滿足]
放松:[個別樣本點不用滿足]
新的目標函數:
C:懲罰因子
(1) 當 C 值比較大時,說明分類比較嚴格,不容有誤。
(2)當 C 值比較小時,說明分類比較寬松,可以有誤。
三、核函數
談一下核函數:
線性不可分情況:
在二維空間無法用一條直線分開,映射到三維 (或者更高維) 空間即可解決。
目標:
找到一個,對原始數據做一個變換。
?
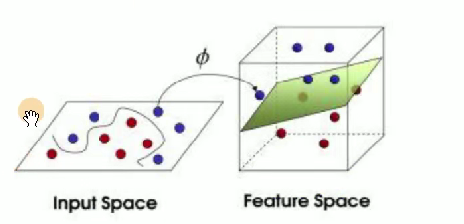
1舉例
????????假設有兩個數據,,
,如果數據在三維空間無法線性可分,我們通過核函數將其從三維空間映射到更高的九維空間,那么此時:
????????如果計算內積的話,x1與x2計算即,此時計算復雜度= 81,原始數據復雜度為\(3*3 = 9\),那么對于映射到n維空間,復雜度為:
????????對于數據點:x1 = (1,2,3),x2 = (4,5,6),則f(x1) = (1,2,3,2,4,6,3,6,9),f(x2) = (16,20,24,20,25,30,24,30,36),此時計算<f(x1)·f(x2)>= 16 + 240 + 72 + 40 + 100 + 180 + 72 + 180 + 324 = 1024
一個巧合
即:[先內積再平方與先映射再內積結果一致]
特性
????????在低維空間完成高維空間的運算,結果一致,大大降低了高維空間計算的復雜度。
本質
????????在找到一個 (核) 函數,將原始數據變換到高維空間,但是高維數據可以在低維運算。
2常用核函數
-
線性核函數:
-
多項式核函數:
-
高斯核函數:
3.多項式核函數
假設有兩個數據,,如果數據在二維空間無法線性可分,我們通過核函數將其從二維空間映射到更高的三維空間,那么此時:
更具體的例子:?
(1) 轉換到三維再內積 (高維運算)
(2) 先內積,再平方 (低維運算)
4.高斯核函數:
? ? ? ? ? ? ??rbf: 又稱徑向基函數
????????對于數據點 1, 轉換到二維空間:
(1) 找兩個地標,或者說兩個數據點,將他們作為一個正態分布的均值。-> 比如 - 2 和 1
(2) 計算數據到地標的距離:
(3) 指定為 0.3.[
必須大于 0]
(4) 計算新的坐標:
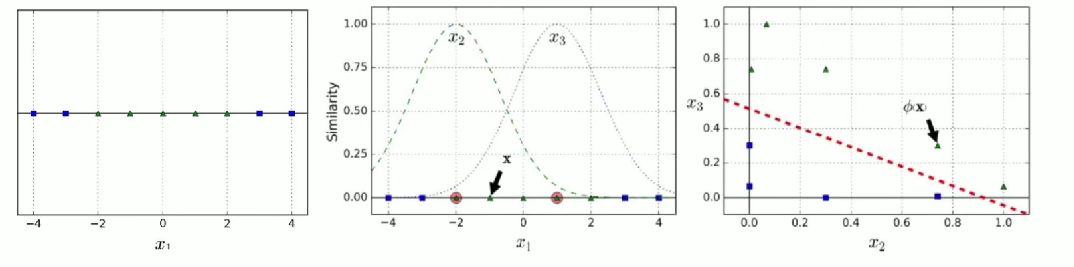
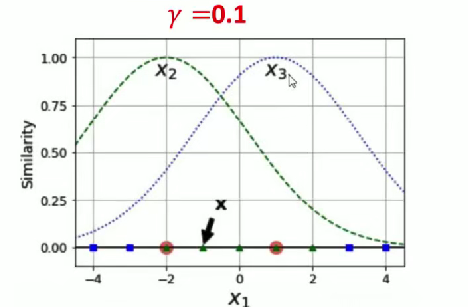
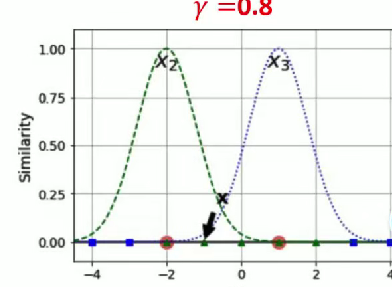
談一下值:
(1) 當值越小的時候,正態分布越胖, 輻射的數據范圍越大,過擬合風險越低。
(2) 當值越大的時候,正態分布越瘦, 輻射的數據范圍越小,過擬合風險越高。
四、svm的優缺點
優點:
- 有嚴格的數學理論支持,可解釋性強,不同于傳統的統計方法能簡化我們遇到的問題。
- 能找出對任務有關鍵影響的樣本,即支持向量。
- 軟間隔可以有效松弛目標函數。
- 核函數可以有效解決非線性問題。
- 最終決策函數只由少數的支持向量所確定,計算的復雜性取決于支持向量的數目,而不是樣本空間的維數,這在某種意義上避免了 “維數災難”。
- SVM 在小樣本訓練集上能夠得到比其它算法好很多的結果。
缺點:
-
對大規模訓練樣本難以實施。
SVM 的空間消耗主要是存儲訓練樣本和核矩陣,當樣本數目很大時該矩陣的存儲和計算將耗費大量的機器內存和運算時間。超過十萬及以上不建議使用 SVM。 -
對參數和核函數選擇敏感。
支持向量機性能的優劣主要取決于核函數的選取,所以對于一個實際問題而言,如何根據實際的數據模型選擇合適的核函數從而構造 SVM 算法。目前沒有好的解決方法解決核函數的選擇問題。 -
模型預測時,預測時間與支持向量的個數成正比。當支持向量的數量較大時,預測計算復雜度較高。
五、支持向量機的API
class sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto_deprecated',coef0=0.0, shrinking=True, probability=False, tol=0.001,cache_size=200, class_weight=None, verbose=False,max_iter=-1, decision_function_shape='ovr', random_state=None)[source]參數解釋(按順序)
-
C- 含義:正則化參數(軟間隔懲罰系數 ),控制 “對分類錯誤的容忍度” 與 “模型復雜度” 的權衡。
- 作用:
C?越大,對錯誤分類懲罰越重(傾向嚴格分類,易過擬合);C?越小,允許更多錯誤(傾向簡化模型,易欠擬合 )。
-
kernel- 含義:核函數類型,決定如何處理非線性關系。
- 可選值:
'linear'(線性核)、'poly'(多項式核 )、'rbf'(高斯核,默認)、'sigmoid'(Sigmoid 核 )等。
-
degree- 含義:僅對?
kernel='poly'(多項式核)有效,指定多項式的次數?n。 - 作用:次數越高,模型擬合能力越強(但也易過擬合 )。
- 含義:僅對?
-
gamma- 含義:核函數的系數(對?
rbf/poly/sigmoid?核生效 ),控制核函數的 “影響范圍”。 - 作用:
gamma?越大,核函數 “聚焦局部”(樣本影響范圍小,易過擬合 );gamma?越小,核函數 “全局化”(影響范圍大,易欠擬合 )。 - 備注:
'auto_deprecated'?是舊版兼容寫法,新版常用?'scale'(按特征方差縮放 )或?'auto'(按特征數倒數縮放 )。
- 含義:核函數的系數(對?
-
coef0- 含義:僅對?
kernel='poly'/'sigmoid'?有效,核函數的獨立項(多項式核的偏移量、Sigmoid 核的截距 )。 - 作用:調整核函數的形狀,對非線性擬合有微調作用。
- 含義:僅對?
-
shrinking- 含義:是否啟用 “支持向量收縮” 優化。
- 作用:加速訓練,默認?
True(建議開啟,尤其是大數據 )。
-
probability- 含義:是否啟用概率估計(基于 Platt 縮放 )。
- 作用:
True?則輸出分類概率(會增加訓練 / 預測時間 ),默認?False。
-
tol- 含義:迭代停止的精度閾值(對偶問題求解的收斂條件 )。
- 作用:
tol?越小,訓練越精細(但耗時 );默認?0.001。
-
cache_size- 含義:核緩存大小(單位:MB ),用于存儲核矩陣以加速計算。
- 作用:內存充足時調大(如?
500)可加速訓練,默認?200。
-
class_weight- 含義:類別權重,解決不平衡數據集問題。
- 可選值:
None(等權重 )、'balanced'(按類別樣本數自動分配權重 ),或字典手動指定(如?{0:1, 1:5}?給類別 1 更高權重 )。
-
verbose- 含義:是否輸出訓練過程的詳細日志。
- 作用:
True?則打印迭代信息(調試用 ),默認?False。
-
max_iter- 含義:最大迭代次數(對偶問題求解的迭代上限 )。
- 作用:
-1?表示無限制(由?tol?決定停止 ),可手動設小值強制提前停止。
-
decision_function_shape- 含義:多分類策略,
'ovr'(一對其余,默認 )或?'ovo'(一對一 )。 - 作用:
'ovr'?更高效,'ovo'?對某些數據集精度更高(但計算量大 )。
- 含義:多分類策略,
-
random_state- 含義:隨機種子(用于初始化、采樣的隨機性控制 )。
- 作用:設固定值(如?
42?)可復現結果,默認?None(隨機 )
六、案例分析
使用支持向量機對鳶尾花進行訓練、現有數據集:
數據讀取與準備
import pandas as pd
# 讀取CSV數據,假設無表頭(header=None)
data = pd.read_csv('iris.csv', header=None)- 讀取鳶尾花數據集,這是一個經典的多類別分類數據集,包含 3 種鳶尾花的特征數據
?數據可視化(原始數據)
import matplotlib.pyplot as plt
# 提取兩類數據(假設前50行為類別0,50-100行為類別1)
data1 = data.iloc[:50, :] # 第一類鳶尾花
data2 = data.iloc[50:100, :] # 第二類鳶尾花# 選擇第2個和第4個特征進行可視化(因為四維數據無法直接展示)
plt.scatter(data1[1], data1[3], marker='+') # 第一類用"+"標記
plt.scatter(data2[1], data2[3], marker='o') # 第二類用"o"標記- 鳶尾花數據集原本有 4 個特征,這里選擇第 2 列和第 4 列特征進行可視化
- 用不同標記區分兩類鳶尾花數據點
SVM 模型訓練
from sklearn.svm import SVC
# 構建特征矩陣X(選擇第2和第4個特征)和標簽y(最后一列是類別)
X = data.iloc[:, [1, 3]]
y = data.iloc[:, -1]# 創建線性核SVM模型,C設為無窮大模擬硬間隔SVM
svm = SVC(kernel='linear', C=float('inf'), random_state=0)
svm.fit(X, y) # 訓練模型# 獲取SVM的權重系數和偏置項
w = svm.coef_[0] # 權重向量
b = svm.intercept_[0] # 偏置項- 使用
sklearn的SVC類構建支持向量機模型 kernel='linear'表示使用線性核函數C=float('inf')表示使用硬間隔(不允許任何樣本被錯誤分類)- 訓練后獲取模型參數:權重系數
w和偏置b,用于構建決策邊界
繪制決策邊界和間隔
import numpy as np
# 生成x軸數據(特征1的取值范圍)
x1 = np.linspace(0, 7, 300)# 計算決策邊界和間隔線(基于SVM的決策函數w·x + b = 0)
x2 = -(w[0] * x1 + b) / w[1] # 決策邊界:w·x + b = 0
x3 = (1 - w[0] * x1 - b) / w[1] # 上間隔:w·x + b = 1
x4 = (-1 - w[0] * x1 - b) / w[1] # 下間隔:w·x + b = -1# 繪制決策邊界和間隔線
plt.plot(x1, x2, linewidth=2, color='r') # 決策邊界(實線)
plt.plot(x1, x3, linewidth=1, color='r', linestyle='--') # 上間隔(虛線)
plt.plot(x1, x4, linewidth=1, color='r', linestyle='--') # 下間隔(虛線)- 決策邊界是 SVM 找到的最優分類線,滿足
w·x + b = 0 - 間隔線表示分類的安全區域,上間隔為
w·x + b = 1,下間隔為w·x + b = -1
調整顯示范圍和繪制支持向量
# 設置坐標軸范圍
plt.xlim(4, 7)
plt.ylim(0, 5)# 獲取并繪制支持向量(對決策邊界有決定性影響的樣本點)
vets = svm.support_vectors_
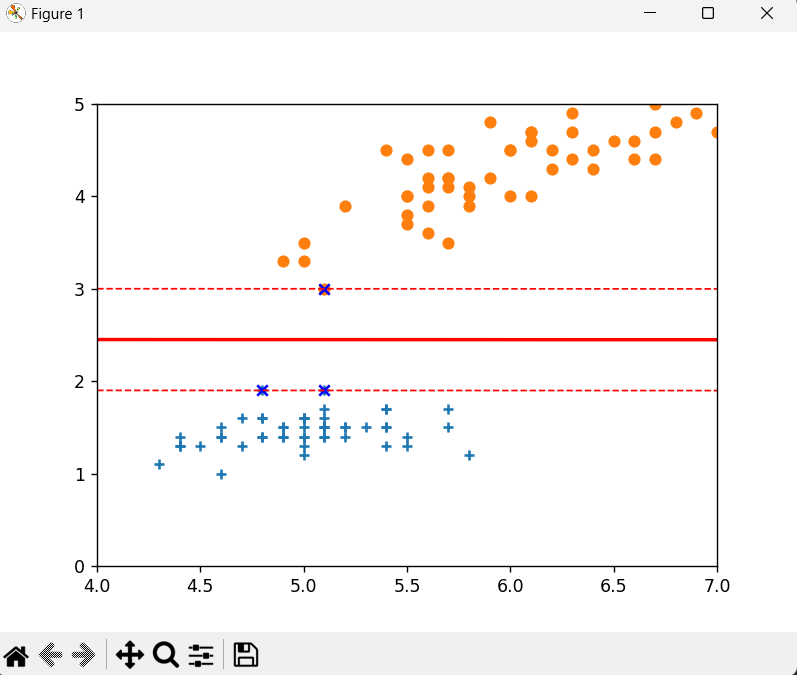
plt.scatter(vets[:, 0], vets[:, 1], c='b', marker='x') # 支持向量用藍色"x"標記plt.show() # 顯示圖像最終結果
- 支持向量是距離決策邊界最近的樣本點,決定了 SVM 的決策邊界位置
- 最終圖像展示了兩類數據點、決策邊界、間隔區域和支持向量
我們還可以使用交叉驗證去尋找最好的模型參數,這里講述了如何用交叉驗證去尋找最好的參數。
機器學習第三課之邏輯回歸(二)LogisticRegression
![P3232 [HNOI2013] 游走,solution](http://pic.xiahunao.cn/P3232 [HNOI2013] 游走,solution)


介紹)

)



如何使用MySQL的慢查詢工具?)
)








