今天又是坐牢的一次比賽,恭喜獲得本次比賽稱號:掛機王,一個簽到題能卡住兩個小時,這兩個小時簡直坐的我懷疑人生,實在是找不出哪里錯了,后來快結束的時候才發現少了一個等于號,也不至于連簽到題都沒寫出來 -_-!。
比賽連接:河南萌新聯賽2025第(四)場:河南大學_ACM/NOI/CSP/CCPC/ICPC算法編程高難度練習賽_牛客競賽OJ
本次出題方給出的題目難度如下:
難度評估
-
簽到:A,C,G,J
-
簡單:B,D,L
-
中等:F,H,I
-
困難:E,K
我做題的順序為G、C、A、J,我也是本本分分地寫了寫簽到題,簡單題甚至都開不出來,既然都比賽結束了,就當又是一次鍛煉了,多多積累一些比賽的思維以及解題技巧,下面就開始補題吧。
G-封閉運算
題目鏈接:G-封閉運算_河南萌新聯賽2025第(四)場:河南大學
剛開始的我竟然找不出來哪一個才是簽到題,???我的Hello World呢?在找了一分鐘之后實在是沒辦法了,就找了一個看著最好欺負的下手了,一看數據范圍,小于100??!,這我還猶豫什么,直接三重循環暴力拿下!
賽時代碼:
// Problem: 封閉運算
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/115184/G
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;void solve()
{int n;cin>>n;int k=1;vector<int> a(n+1);for(int i=1;i<=n;i++) cin>>a[i];bool f = 1;for(int i=1;i<=n;i++){for(int j=i;j<=n;j++){int t = a[i] | a[j];//異或操作for(k=1;k<=n;k++){if(t == a[k]){break;}}if(k == n+1){f = 0;break;}}}if(f) cout<<"YES"<<endl;else cout<<"NO"<<endl;
// cout<<fixed<<setprecision(x)<< ;
}signed main()// Don't forget pre_handle!
{IOSint T=1;
// cin>>T;while(T--) solve(); return 0;
}
接下來是廣告時間:有小伙伴對位運算還不是很了解的,可以點擊此處一秒邁入位運算的世界!
C-合并石子
題目鏈接:C-合并石子_河南萌新聯賽2025第(四)場:河南大學
這道題我們要求出最少消耗的體力,具體是讓所有的石子扔到哪一堆呢?看起來似乎很難找出規律,既然這樣,就要開始枚舉了,大體思路如下:
由題意可得,所有石子最后一定會合并到某一個位置,可以枚舉最終位置,取所有情況中所花費體力的最小值。
對于位置x,在 [1,x-1]?區間中的石子一定會不斷向x合并,在區間 [x+1,n]?區間中的石子也一定會不斷向x合并。
由于每次合并是向上取整的,所以從離x置最遠的石子開始合并一定更優,預處理前綴和后綴的體力消耗便可以O(1)的時間復雜度得到合并到位置x所花費體力的最小值。
所以 總的時間復雜度為O(N)。
這種思想是很常見的一種算法思維了,正向和逆向分別跑一遍就能求出每個點兩端的情況(代價)接下來就遍歷一遍所有的點取最值就行了。
賽時代碼如下:
// Problem: 合并石子
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/115184/C
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 1e18;//不要用0x3f3f3f3f了,這道題的數據較大,用這個會WA的 別問我怎么知道的void solve()
{int n,m;cin>>n>>m;vector<int> a(n+1),l(n+2,0),r(n+2,0);for(int i=1;i<=n;i++) cin>>a[i];int ans=inf,sum=0;for(int i=1;i<=n;i++)//正向跑一遍求出每個點所需的體力值{int t = sum / m;if(sum % m) t++;l[i] = t;sum += a[i];}sum = 0;for(int i=n;i>=1;i--)//逆向跑一遍求出每個點所需的體力值{int t = sum / m;if(sum % m) t++;r[i] = t;sum += a[i];}//因為是求的單個點的,所以還需要用前綴和與后綴和來統計到達該點一共所需的體力值for(int i=1;i<=n;i++) l[i] = l[i] + l[i-1];//前綴和for(int i=n;i>=1;i--) r[i] = r[i+1] + r[i];//后綴和//最后只需要遍歷一遍求出最小體力就行了for(int i=1;i<=n;i++) ans = min(ans,l[i] + r[i]);cout<<ans<<endl;// debug:// for(auto i : l) cout<<i<<' ';// cout<<endl;// for(auto i : r) cout<<i<<' ';
// cout<<fixed<<setprecision(x)<< ;
}signed main()// Don't forget pre_handle!
{IOSint T=1;
// cin>>T;while(T--) solve(); return 0;
}
這道題需要注意的就是inf(無窮大)不能用0x3f3f3f3f,不然會wa的,可以用1e18來賦值給 inf
A-完美序列
題目鏈接:A-完美序列_河南萌新聯賽2025第(四)場:河南大學
這道題第一眼除了暴力跑一遍枚舉所有的情況就想不出更好的辦法了,可是看了一眼數據范圍2e5這我怎么跑?本來都想放棄了,可是后來又看了一眼數據范圍,雖然元素的個數是2e5,但是元素的大小范圍只有5000啊!我的思路想法瞬間就有了,枚舉所有可能的和!對,就是這樣,這樣的時間復雜度是....兩個數的和最大不超過10000,然后每個數都大小是5000,所以是5e7,剛好擦邊,嘶~,我的心情瞬間又跌入了谷底,一看時間要求,誒?2s?我瞬間來了斗志,直接暴力將代碼寫了出來,在CP-Editor上信心滿滿的一運行!誒???:
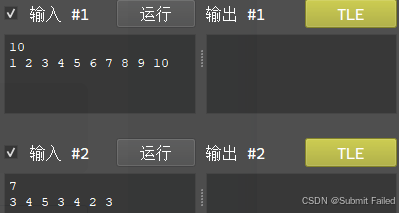
這怎么T了?當時的天又塌了,后來開始去想優化的方法,首先K是不能再少了的,那就看看內層循環能不能減少一部分,對于枚舉的每一個和K,我們其實只需要枚舉到K/2就行了啊,因為我們已經用map存放所有的元素了,枚舉i的時候K -?i是可以直接算出來的,所以就可以在這里進行一個優化,想到這里,我立馬開始了更改,果不其然,代碼跑出來了:
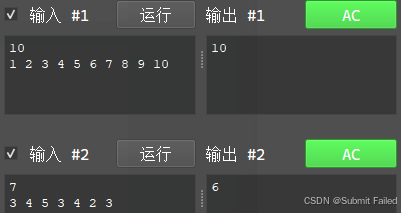
嘶~,舒服多了,提交上去:

沒錯!天又塌了!這怎么會錯呢?都這么暴力了!后來才發現最后的結果必須是偶數,所以少了一個判斷,總的來說,這道題的解題思路如下:
我們在枚舉和K的時候,如果當前內層循環所遍歷的i存在,并且k-i也存在,那么我們就需要判斷兩個數時候相等了,如果i和k-i不相等的話,直接就是讓t累加到兩個數出現的次數的最小的那個再*2就行了,但如果是兩個數相等,即 i == k-i 的時候,就說明是只有這一個了,就不需要*2,直接加上就行了,但是需要注意的是有可能在這里加的是一個奇數,所以需要在最后進行判斷,如果答案是奇數的話就需要--。
我趕緊加上了最后的判斷,再提交!

舒服了,賽時代碼如下:
// Problem: 完美序列
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/115184/A
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;void solve()
{int n;cin>>n;unordered_map<int,int> mp;vector<int> a(n+1);for(int i=1;i<=n;i++){cin>>a[i];mp[a[i]]++;//統計每一個元素出現的次數}int res = 0;for(int k=10002;k>1;k--)//暴力枚舉素所有可能的和K{int t = 0;for(int i=1;i<=k/2;i++)//小優化{if(mp[i] > 0 && mp[k-i] > 0)//只有兩半都存在的時候才有能組成K{// cout<<t<<' ';t += 2 * min(mp[i],mp[k-i]);//如果i == k - i了,就需要減去多加的一組if(i * 2 == k) t -= min(mp[i],mp[k-i]);}}// cout<<"k = "<<k<<" "<<t<<endl;res = max(res,t);//每次更新最大值}if(res & 1) res --;//如果最后的答案為奇數了,就說明在在枚舉的i == k - i的時候加上了奇數 需要減去一個cout<<res<<endl;
// cout<<fixed<<setprecision(x)<< ;
}signed main()// Don't forget pre_handle!
{IOSint T=1;
// cin>>T;while(T--) solve(); return 0;
}
這道題讓我真正體驗到了ACM的魅力,隨著一陣陣的興奮和隨之而來的沉默,隨著苦思冥想突然靈光一現!這中心情和心態的起起伏伏和一波三折,以及看到自己優化的代碼通過了這道題,這種感覺是很難描述的,那一瞬間真的能消除所有的疲憊!希望我們都能得到自己滿意的結果!
J-故障機器人的完美牌組
題目鏈接:J-故障機器人的完美牌組_河南萌新聯賽2025第(四)場:河南大學
這是一道貪心的題目,給我的感覺很像最近這幾天刷的cf上的題目,也就是因為這道題卡了我兩個多小時,題目的意思十分容易理解,貪心的思路也很好想出來:就是從第二個數開始往后找,找出最大的那一個數讓它和第一個數進行累加,最后刪除這個數就是字典序最大的情況了,而如果最大的都是0的話,即從第二個數開始后面的數都是0的話,就沒必要進行操作了,因為不管怎么加第一個數都保持不變,而要想讓字典序最小的話,就直接將原數組輸出進行了,因為原數組與操作后的數組相比,元素更多,長度更長,字典序也就相對更大。這就是貪心的思路,可是我在編譯器上通過之后,隨之而來的就是:
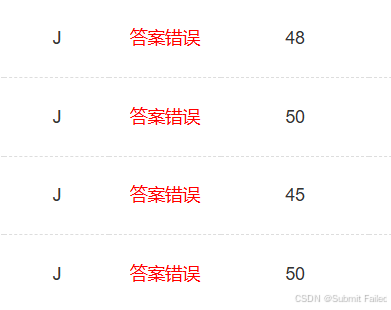
嘶~怎么回事,這還不貪???我苦苦想了半天都沒有想出來需要特判的地方了,當時我的思路都開始混亂了,于是我想到了之前的隊友跟我說的一句話:如果你覺得你的思路沒有啥大問題,就重新敲一遍代碼,也許就是你的代碼太亂了有些細節忽略了,于是我又重新敲了一遍,并且還換了一種碼風,在題目的樣例和自己造的樣例都通過之后又交了上去:

呵呵,這時候心都涼半截了,沒辦法,各種姿勢開始想哪里的問題,終于在比賽結束的四十分鐘前,我突然想到了一個問題,想讓字典序最大,那我在找最大值的時候,如果有多個最大值的話,我就需要讓大的盡量在前面,所以我就需要將最后一個最大值來與第一個進行替換!比如說樣例1202,我們需要將最后一個2與第一個匹配為320而不是讓第一個2與之匹配變為302,于是我立馬將小于換為了小于等于,不信邪的又交了一發:

又舒服了,此時我看著所剩的寥寥無幾的比賽時間和別人WA了七八發的下一道題,逐漸陷入了沉思.....不過很容易能看出來下一道題L考察的是素數篩,素數篩我前幾天也整理過一篇博客,有興趣的話可以點擊這里:數論中的常用模板,但是賽時就是想不起來怎么篩了,還有B題,可以看出來是整除分塊,但是具體怎么分還是沒有思路,在上面的這篇博客中也有提到,emmm,剩下的題目明天再補,大家盡請期待!
J題的賽時代碼:
// Problem: 故障機器人的完美牌組
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/115184/J
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;void solve()
{int n;cin>>n;bool f = 1;vector<int> a(n+5,0);for(int i=1;i<=n;i++) cin>>a[i];int mx = -1,index = -1;if(n == 1)//對1的情況進行特判{cout<<1<<endl;cout<<a[1]<<endl;return ;}for(int i=2;i<=n;i++){if(mx <= a[i])//一定是等于 要找最后一個最大值{mx = a[i];index = i;}if(a[i] > 0) f = 0;//找到了一個非0的數字}//甚至都懷疑過是三目運算符的問題...// cout<<(f == 0 ? n-1 : n)<<endl;if(f)//全部都是0的話就將原數組輸出就行了 此時原數組的字典序就最大{cout<<n<<endl;for(int i=1;i<=n;i++) cout<<a[i]<<' ';}else//有最大值的話就將最后一個最大值賦值給第一個元素 然后將其刪除就行了{cout<<n-1<<endl;a[1] += mx;for(int i=1;i<=n;i++){if(i == index) continue;//跳過這個元素 因為這個元素已經被刪除了 和第一個元素進行累加了cout<<a[i]<<' ';}}
// cout<<fixed<<setprecision(x)<< ;
}signed main()// Don't forget pre_handle!
{IOSint T=1;// cin>>T;while(T--) solve(); return 0;
}

免安裝中文版)




)






)





