學習完string類、容器vector和容器list，再去學習其他容器的學習成本就非常低，容器的使用方法都大差不差，而棧和隊列的底層使用了適配器，去模擬實現就沒有那么麻煩，適配器也是一種容器，但是這種容器兼備棧和隊列需要的特性，通過觀察棧和隊列的碼源更能體會到適配器的方便和厲害之處。雖然stack和queue中也可以存放元素，但在STL中并沒有將其劃分在容器的行列，而是將其稱為容器適配 器，這是因為stack和隊列只是對其他容器的接口進行了包裝，STL中stack和queue默認使用deque。

目錄

雙端隊列：deque

deque的優缺點

棧和隊列的模擬實現

?優先級隊列的模擬實現

priority_queue初始化

向下調整和向上調整算法

priority_queue插入和刪除

?priority_queue其它接口

對比總結

---

雙端隊列：deque

如果熟悉一個容器的使用對于其他容器也能很快上手，所以小編在這里就不講棧和隊列的使用了，在還未學習c++之前，小編學習了數據結構雖然是C語言版的，也是初步了解了棧和隊列。在C語言中棧和隊列的實現，棧的特點是先進后出，是用數組來實現的，棧需要pop和top來刪除數據和去數據但是在尾部，所以用一個數組就能很好的解決。隊列的特點是先進先出，需要頻繁的頭刪，如果使用數組來實現效率不高，數組頭刪的時間復雜度為O(N)，所以鏈表就是一個很好的選擇。在c++中究竟是什么樣的容器既能符合棧的特征，又能符合隊列的特征，讓我們一起往下瞧瞧吧！

在棧和隊列中哪里可以用到deque呢？deque在模版中，在棧和隊列顯示實例化中默認的適配器是deque，當然也可以手動傳vector或者list。

?雙端隊列原理：deque(雙端隊列)：是一種雙開口的"連續"空間的數據結構，雙開口的含義是：可以在頭尾兩端進行插入和刪除操作，且時間復雜度為O(1)，與vector比較，頭插效率高，不需要搬移元素；與list比較，空間利用率比較高。

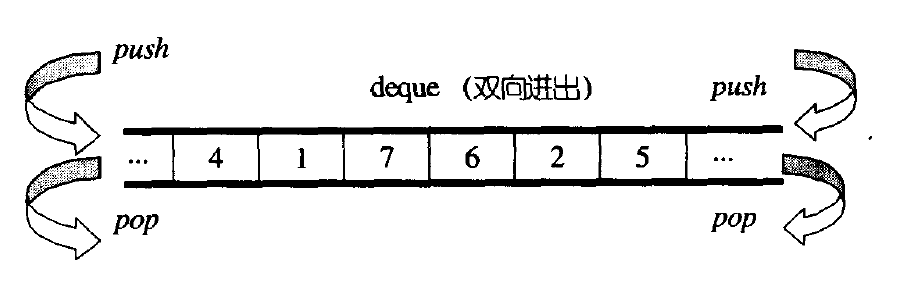
但是雙端隊列并不是這樣連續的空間，而是像二維數組一樣，一個指針數組，每個指針都對應著一塊空間。

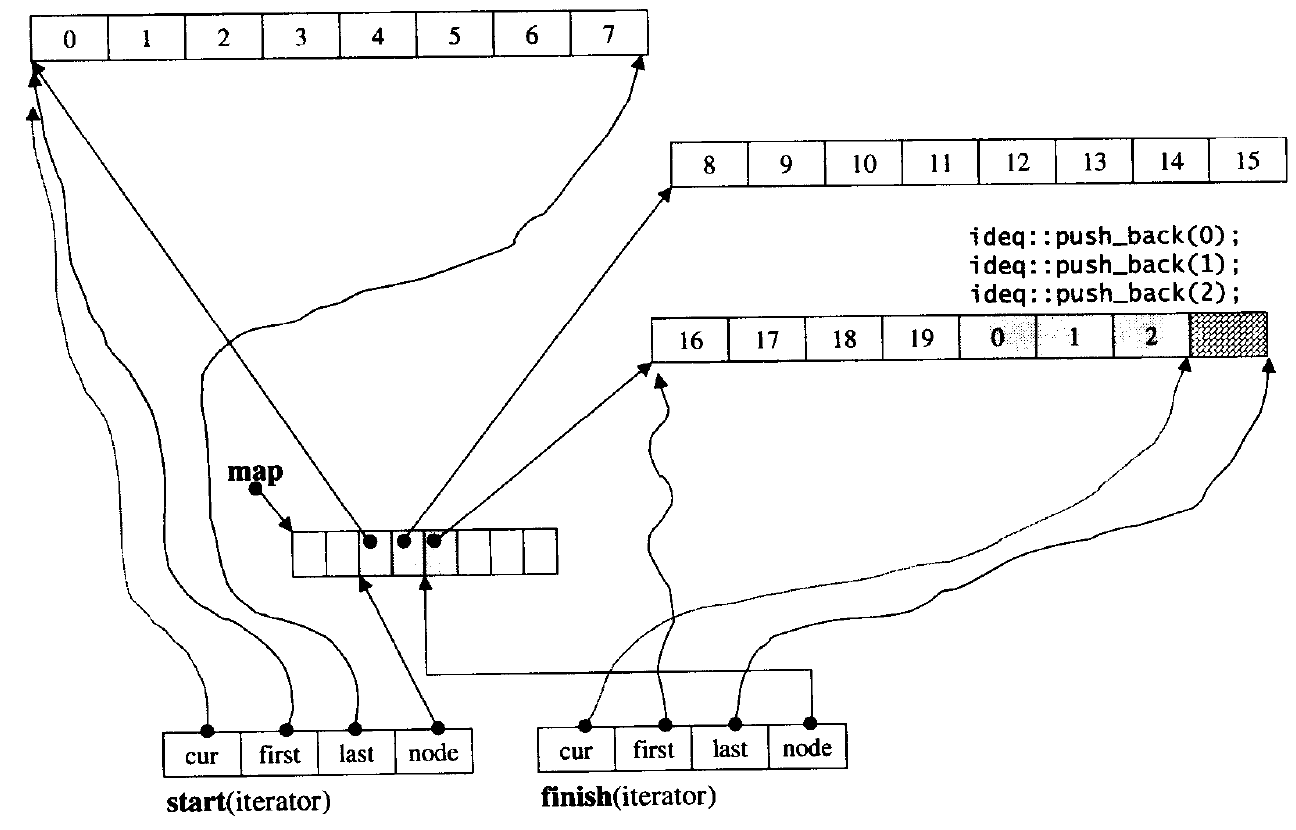?從上面的圖中可以看出迭代器中node是當前結點，cur指向當前數組位置，用來迭代器訪問元素，first和last分別指向每個節點對應的數組的起始位置和末尾。當cur等于last，node就要指向下一個節點，cur又在起始位置了，雖然這些空間不連續，但是可以重載一些函數來定義其行為以及封裝看似空間時連續的。

deque的優缺點

優點：與vector比較，deque的優勢是：頭部插入和刪除時，不需要搬移元素，效率特別高，而且在擴容時，也不需要搬移大量的元素，因此其效率是必vector高的。

與list比較，其底層是連續空間，空間利用率比較高，不需要存儲額外字段。

缺點：deque有一個致命缺陷：不適合遍歷，因為在遍歷時，deque的迭代器要頻繁的去檢測其是否移動到某段小空間的邊界，導致效率低下，而序列式場景中，可能需要經常遍歷，因此在實際中，需要線性結構

時，大多數情況下優先考慮vector和list，deque的應用并不多，而目前能看到的一個應用就是，STL用其作為stack和queue的底層數據結構。

那么為什么要用deque來作為stack和Queue的默認底層容器呢？?

首先stack是一種后進先出的特殊線性數據結構，因此只要具有push_back()和pop_back()操作的線性結構，都可以作為stack的底層容器，比如vector和list都可以；queue是先進先出的特殊線性數據結構，只要具有 push_back和pop_front操作的線性結構，都可以作為queue的底層容器，比如list。

但是STL中對stack和 queue默認選擇deque作為其底層容器，主要是因為： 1. stack和queue不需要遍歷(因此stack和queue沒有迭代器)，只需要在固定的一端或者兩端進行操作。 2. 在stack中元素增長時，deque比vector的效率高(擴容時不需要搬移大量數據)；queue中的元素增長 時，deque不僅效率高，而且內存使用率高。 結合了deque的優點，而完美的避開了其缺陷。

棧和隊列的模擬實現

在學習C語言階段，模擬實現了棧和隊列，需要的代碼量需要幾百行，自己造輪子還是比較麻煩的，而在C++中有現成的不需要我們去造輪子，模擬實現棧和隊列就輕松多了，deque作為默認的底層容器。

stack代碼示例：

template<class T, class Con = deque<T>>class stack{public:void push(const T& x){_c.push_back(x);}void pop(){_c.pop_back();}T& top(){return _c.back();}const T& top()const{return _c.back();}size_t size()const{return _c.size();}bool empty()const{return _c.empty();}private:Con _c;};

Queue代碼示例：

template<class T, class Con = deque<T>>class queue{public:void push(const T& x){_c.push_back(x);}void pop(){_c.pop_front();}T& back(){return _c.pop_back();}const T& back()const{return _c.pop_back();}T& front(){return _c.front();}const T& front()const{return _c.pop_front();}size_t size()const{return _c.size();}bool empty()const{return _c.empty();}private:Con _c;};

?優先級隊列的模擬實現

優先級隊列的底層結構是堆，還是又vector作為容器來實現，而模擬實現優先級隊列就需要建堆，在STL中優先級隊列默認是大堆，所以在模擬實現中我們也是大堆。在模擬實現的過程中可以發現自己的對知識的疏漏，在建堆和什么時候使用向下調整和向上調整出現了問題，也導致了花費有些時間去復習以前的知識。優先級隊列畢竟是隊列，還有先進先出的特性，在隊列插入元素實在末尾插入，需要根據大小堆來進行向上調整，刪除頭元素如果直接進行刪除就會大大降低效率，可以先和末尾元素交換，接著刪除末尾元素，在從根結點開始向下調整，使堆保持大堆或者小堆。

在實現之前需要三個模版參數：

 template <class T, class Container = vector<T>, class Compare = less<T> >

?T是數據的類型，Container是適配器，也就是優先級隊列的底層容器，默認容器是vector，compare是仿函數，來控制大堆或者小堆也就是數據的排升降序。注意：這里的less用的是庫里面的

變量：

private:Container c;Compare comp;

priority_queue初始化

 priority_queue(){}template <class InputIterator>priority_queue(InputIterator first, InputIterator last){while (first != last){c.push_back(*first);++first;}for (int i = (size()-2)/2; i >= 0; i--){Adupdown(i);}}

構造函數對內置類型不做處理，對于自定義類型會調用自己的構造函數，所以默認構造不需要寫，而用迭代器初始化需要建堆，堆的特性使得它能在O(1)時間內獲取最高（或最低）優先級的元素，并在O(log n)時間內完成插入和刪除操作，這與優先級隊列的需求高度契合。堆的結構保證了根節點始終是最大（或最小）元素，每次插入或刪除后，堆會通過“上浮”或“下沉”操作重新調整結構，確保優先級順序始終正確。?

向下調整和向上調整算法

void Adupdown(int parent)//向下調整{int child = parent * 2 + 1;while (child < c.size()){if (child + 1 < c.size() && comp(c[child],c[child+1])){child++;}if (comp(c[parent], c[child])){swap(c[parent], c[child]);parent = child;child = parent * 2 + 1;}else{break;}}}

 void Adjustup(int child)//向上調整{int parent = (child - 1) / 2;while (child > 0){if (comp(c[parent] , c[child])){swap(c[parent], c[child]);child = parent;parent = (child - 1) / 2;}else{break;}}}

向下調整通常用于刪除堆頂元素或構建堆時,向下調整從根節點開始。向上調整通常用于插入新元素時。將新元素添加到堆的末尾，然后通過向上調整來恢復堆的性質,向上調整從新插入的節點開始。?

priority_queue插入和刪除

每次插入一個元素就需要向上調整來保持大堆或者小堆，而刪除元素也是方便，首位元素進行交換，再刪除末尾元素，比直接刪除頭元素效率更高。

代碼示例：

void push(const T& x){c.push_back(x);Adjustup(size() - 1);}void pop(){swap(c[0], c[c.size() - 1]);c.pop_back();Adupdown(0);}

?priority_queue其它接口

 bool empty() const{return c.empty();}size_t size() const{return c.size();}const T& top() const{return c[0];}

對比總結

特性	雙端隊列	優先級隊列
操作位置	頭部和尾部均支持操作	僅支持從優先級最高端操作
底層實現	數組或鏈表	通常為堆（Heap）
時間復雜度	插入/刪除：O(1)（均攤）	插入/刪除：O(log n)
典型用途	雙向數據處理、滑動窗口	動態優先級任務處理