A. Recycling Center

題目大意

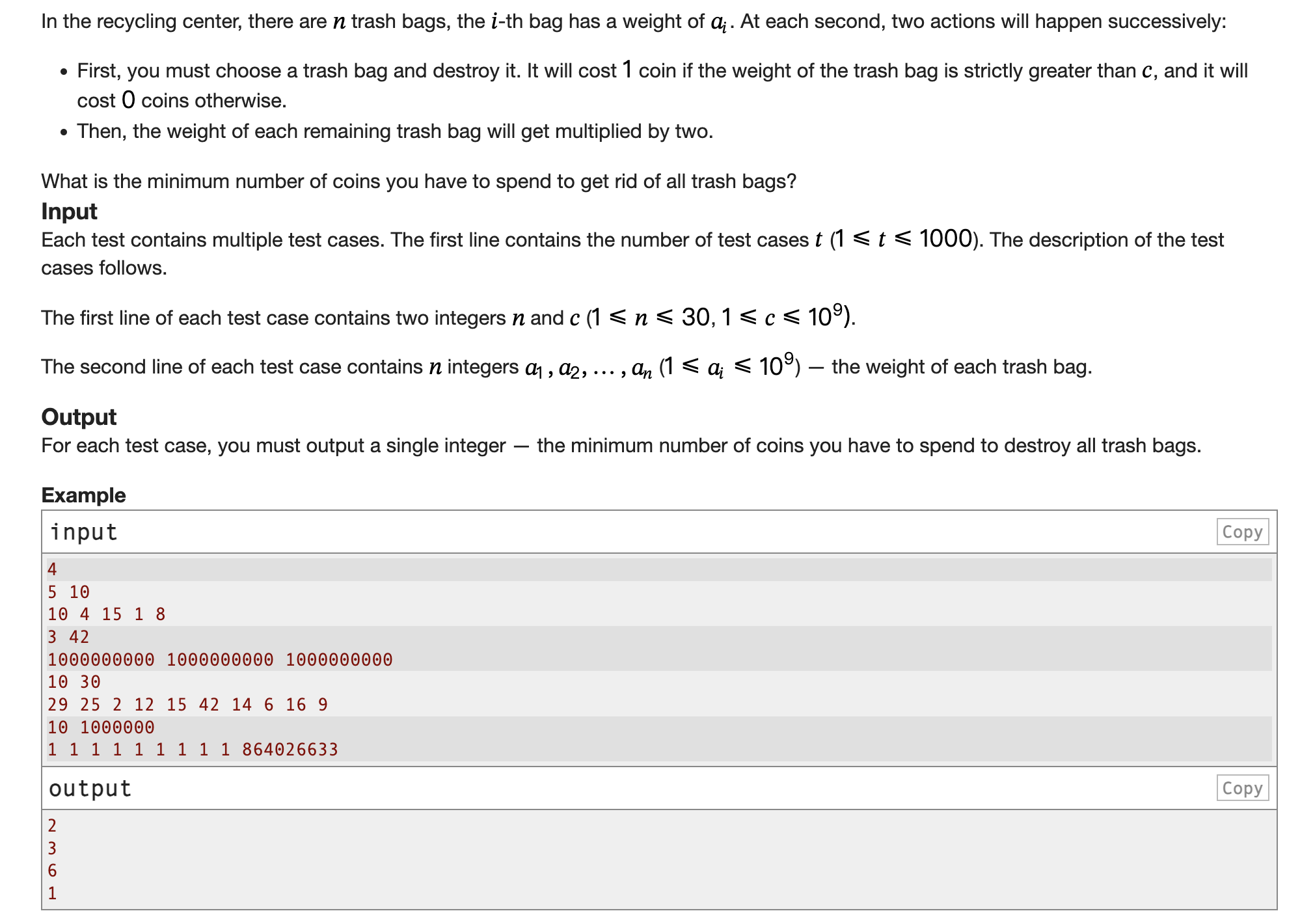
給你n個垃圾袋，每個垃圾袋有一個重量
在每秒鐘，你可以選擇一個垃圾袋，如果他的重量小于等于c，那么你可以不花費硬幣丟掉它
當你丟掉一個垃圾袋后，其他垃圾袋在這一秒重量會翻倍
問最少花費幾個硬幣可以丟掉所有垃圾袋

思路

使用優先隊列
從大到小存儲所有垃圾袋
對于大于c的垃圾袋，無論如何都要丟掉，答案加1
對于小于c的垃圾袋，我們丟掉最大的小于等于c的垃圾袋
可以想到如果要盡可能多的丟掉小于等于c的垃圾袋，這一定是最優的

// Author: zengyz
// 2025-08-02 20:25#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{ll n, c;cin >> n >> c;vector<ll> a(n);priority_queue<ll, vector<ll>, less<ll>> pq;for (ll i = 0; i < n; i++){cin >> a[i];pq.push(a[i]);}ll ans = 0;ll now = 1;while (pq.size()){while (pq.size() && pq.top() * now > c){pq.pop();ans++;}if (pq.size() == 0)break;pq.pop();now *= 2;}cout << ans << endl;return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}

B. Deque Process

思路

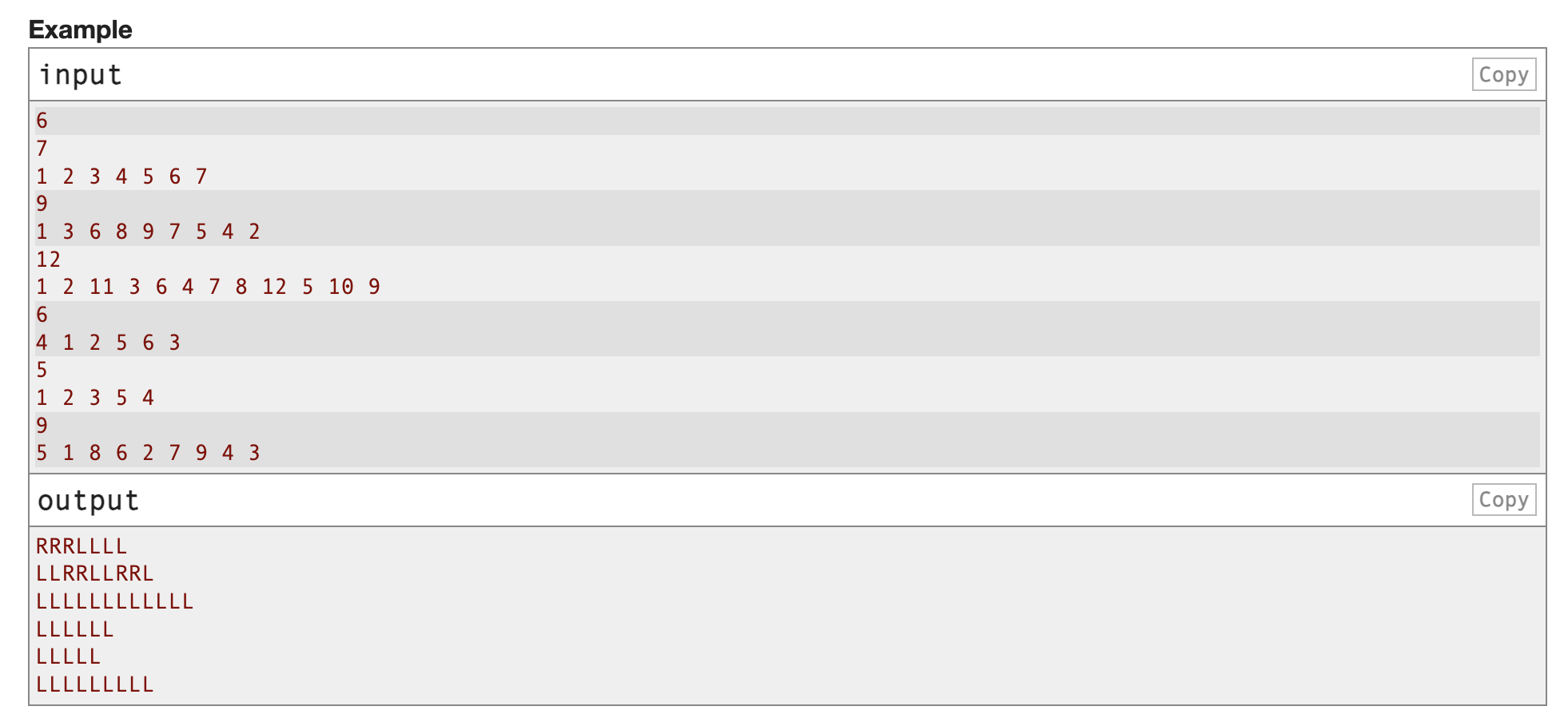
我們在奇數時間選擇兩端較小的一個，偶數時刻選擇較大的一個，可以證明這一定是好的

證明：
考慮奇數時間
$q_i=min(p_l,p_r)$,假設最小值是$p_r$,那么$p_l>p_r$
考慮偶數時間
$q_{i+1}=max(p_l,p_{r?1})$
所以$q_{i+1}$一定大于$q_i$
同理$q_{i+2}$一定小于$q_{i+1}$

// Author: zengyz
// 2025-08-02 20:48#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int n;cin >> n;vector<int> a(n);for (int i = 0; i < n; i++)cin >> a[i];int l = 0, r = n - 1;vector<char> ans;int now = 0;while (l <= r){if (!now){if (a[l] < a[r]){ans.push_back('L');l++;}else{ans.push_back('R');r--;}}else{if (a[l] > a[r]){ans.push_back('L');l++;}else{ans.push_back('R');r--;}}now ^= 1;}for (int i = 0; i < ans.size(); i++)cout << ans[i];cout << endl;return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}

C. Leftmost Below

題目大意

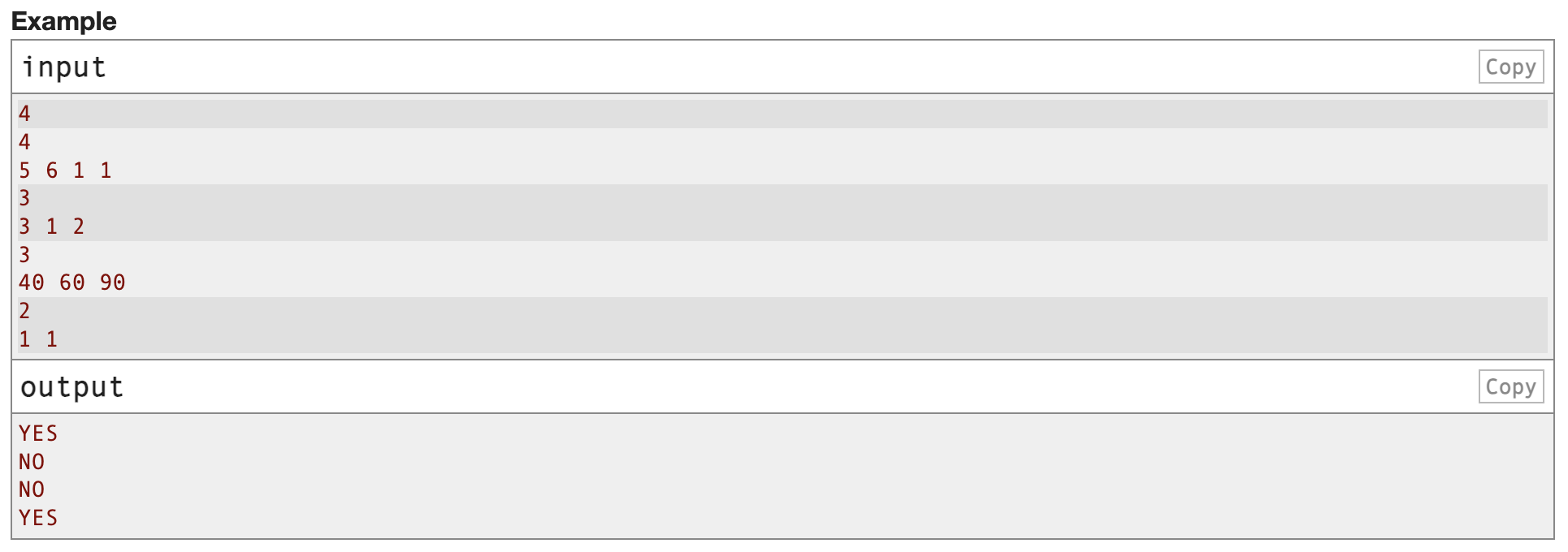
給你一個全0的數組a
每次操作如下：
選擇一個大于數組a最小值的值x
定義i為數組a中第一個小于x的值的下標，將其加x
問能否變成數組b

思路

設minn為從左到右數組b的最小值
當考慮到第i個元素時，如果$b_i\le minn$,那么我們可以直接添加$b_i$
如果$b_i>minn$ 我們可以先添加 $minn?1$ 再添加$minn$
如果大于等于兩倍minn則無解

// Author: zengyz
// 2025-08-02 20:57#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int n;cin >> n;vector<ll> a(n);for (int i = 0; i < n; i++){cin >> a[i];}ll maxx = a[0];bool flag = true;for (int i = 1; i < n; i++){if (2 * maxx <= a[i]){flag = false;break;}maxx = min(maxx, (ll)a[i]);}if (flag){cout << "YES" << endl;}elsecout << "NO" << endl;return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}