哈希概念

順序結構以及平衡樹中，元素關鍵碼與其存儲位置之間沒有對應的關系，因此在查找一個元素時，必須要經過關鍵碼的多次比較。順序查找時間復雜度為$O(N)$，平衡樹中為樹的高度，即$O({\log }_{2}N)$，搜索的效率取決于搜索過程中元素的比較次數。

理想的搜索方法：可以不經過任何比較，一次直接從表中得到要搜索的元素。

如果構造一種存儲結構，通過某種函數（hashFunc）使元素的存儲位置與它的關鍵碼之間能夠建立一一映射的關系，那么在查找時通過該函數可以很快找到該元素。

當向該結構中插入元素：

• 根據待插入元素的關鍵碼，以此函數計算出該元素的存儲位置并按此位置進行存放。

當向該結構中搜索元素：

• 對元素的關鍵碼進行同樣的計算，把求得的函數值當做元素的存儲位置，在結構中按此位置取元素比較，若關鍵碼相等，則搜索成功。

該方式即為哈希（散列）方法，哈希方法中使用的轉換函數稱為哈希（散列）函數，構造出來的結構稱為哈希表（Hash Table，或者稱散列表）。因此哈希更像是一種算法思想，類似貪心、分治等，哈希表是用這個思想實現的一種數據結構。

常見的哈希

其他哈希

1. 直接定址法

取關鍵字的某個線性函數為散列地址：$\text{Hash}(\text{Key})=\text{A}\times \text{Key?+?B}$。

優點是簡單、均勻，缺點是需要事先知道關鍵字的分布情況。

使用場景：適合查找比較小且連續的情況。

例如{2,5,3,99,33,99999,888,34}，因為最大值和最小值差距過大，用直接定址會浪費大量的空間。

2. 除留余數法

設散列表中允許的地址數為m，取一個不大于m，但最接近或者等于m的質數p作為除數。

按照哈希函數：$\text{Hash(key)?=?key}\%p(p\le m)$，將關鍵碼轉換成哈希地址。

但容易出現哈希沖突（或哈希碰撞）：不同的值的哈希值相同。

例如：數據集合{1，7，6，4，5，9}；哈希函數設置為：$\text{hash(key)?=?key}\%\text{capacity}$; capacity為存儲元素底層空間總的大小。

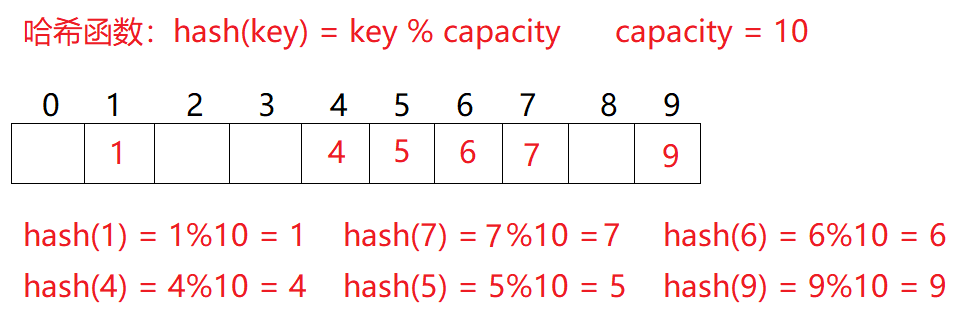
用該方法進行搜索不必進行多次關鍵碼的比較，因此搜索的速度比較快。除留取余法也是學習的重點。

可以通過數學證明，當p或capacity為質數時，產生沖突的概率最小。

3. 平方取中法(了解)

假設關鍵字為1234，對它平方就是1522756，抽取中間的3位227作為哈希地址；再比如關鍵字為4321，對它平方就是18671041，抽取中間的3位671(或710)作為哈希地址。

平方取中法比較適合：不知道關鍵字的分布，而位數又不是很大的情況。

因為用的比較少，就只簡單提及。

4. 折疊法(了解)

折疊法是將關鍵字從左到右分割成位數相等的幾部分(最后一部分位數可以短些)，然后將這幾部分疊加求和，并按散列表表長，取后幾位作為散列地址。

折疊法適合事先不需要知道關鍵字的分布，適合關鍵字位數比較多的情況。

因為用的比較少，就只簡單提及。

5. 隨機數法(了解)

選擇一個隨機函數，取關鍵字的隨機函數值為它的哈希地址，即$\text{H(key)?=?random(key)}$，其中 $\text{random}$ 為隨機數函數。通常應用于關鍵字長度不等時采用此法。

因為用的比較少，就只簡單提及。

6. 數學分析法(了解)

設有n個d位數，每一位可能有 r 種不同的符號，這 r 種不同的符號在各位上出現的頻率不一定相同，可能在某些位上分布比較均勻，每種符號出現的機會均等，在某些位上分布不均勻只有某幾種符號經常出現。可根據散列表的大小，選擇其中各種符號分布均勻的若干位作為散列地址。例如：

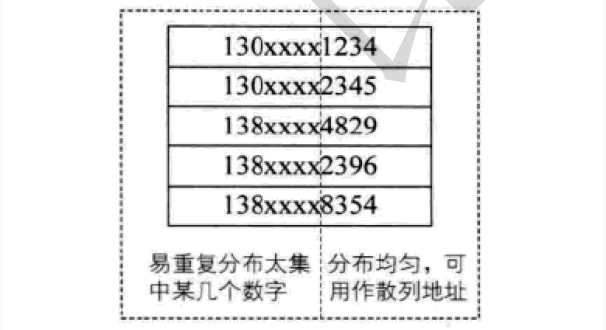
假設要存儲某家公司員工登記表，如果用手機號作為關鍵字，那么極有可能前7位都是 相同的，那么我們可以選擇后面的四位作為散列地址，如果這樣的抽取工作還容易出現 沖突，還可以對抽取出來的數字進行反轉(如1234改成4321)、右環位移(如1234改成4123)、左環移位、前兩數與后兩數疊加(如1234改成12+34=46)等方法。

數字分析法通常適合處理關鍵字位數比較大的情況，如果事先知道關鍵字的分布且關鍵字的若干位分布較均勻的情況。

因為用的比較少，就只簡單提及。

字符串哈希（算法競賽常用）

在算法競賽中，有時會對長度為$m$字符串進行這樣的處理：

選取 2 個互質常數 b 和 h ，b < h，設字符串$C=c_1{c}_2?c_m$，則可定義哈希函數

$H(C)=(c_1{b}^{m?1}+c_2{b}^{m?2}+?+c_m{b}^0)\mathrm{mod}h$。

這個定義和進制數很像，在某種意義上也可以把$H(C)$看作是 $b$ 進制數。和進制數類似就意味著這個表達式可以通過遞推實現：

$H(C_{k+1})=H(C_k)\times b+c_{k+1}$，$0\le k\le m$。

在實際應用中，最常見的做法是 hash 值用無符號數存儲，這樣就可以省略對 hash 值取模的操作（無符號數溢出自動取模）。所以字符串哈希實質就是將字符串用一個整數來表示。舉個例子，$\text{C=abcd}$，

$H(C_0)=97$，97是 $a$ 的 ASCII 碼值，也可以使用序號0、1表示。
$H(C_1)=H(C_0)\times b+98=97b+98$，
$H(C_2)=H(C_1)\times b+99=H(C_0)\times b^2+98b+99=97b^2+98b+99$，
$H(C_3)=H(C_2)\times b+100=97b^3+98b^2+99b+100$。

字符串哈希主要解決字符串匹配問題：尋找長度為 $n$ 的主串 $S$ 中的匹配串 $T$ （假設長度為 $m$）的出現次數或出現位置。盡管 c++ 的string自帶find函數，STL工具里也有類似的工具，但那些工具的實現方式是暴力匹配（Brute Force）算法，時間復雜度$O(n\times m)$，在主串和匹配串的長度乘積數量級超過$10^8$時就有超時的風險（指大多數OJ運行時長限制為 1 秒）。

字符串哈希的準備工作的時間復雜度是$O(n+m)$，查詢匹配串的時間復雜度為$O(n?m)$。具體查詢方法：

例如匹配串$\text{T=bc}$，查詢$T$在$C$中的位置時，有
$H(T)=H(C_{0+2})?H(C_0)\times b^2=97b^2+98b+99?97b^2=98b+99$。

通用的查詢公式：
$H(T)=H(C_{i+len})?H(C_i)\times b^{len}$。（下標從0開始計數）

查詢匹配串時，需要計算不同長度的字符串的哈希值存儲在數組中。之后從開頭遍歷到$n?m$，利用公式進行判斷即可。

且通過字符串哈希算法可將字符串轉換成數字時，也可以通過直接定址法或除留取余法存入哈希表。只需要對庫中的獲取哈希值的仿函數做一個字符串的特化即可。但無論質數如何取，都無法完全避免哈希沖突。

字符串哈希OJ

P3370 【模板】字符串哈希 - 洛谷

P3370 【模板】字符串哈希 - 洛谷

模板題，將所有字符串的哈希值計算出來，放入set或unordered_set中去重即可。

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ULL;
set<ULL>a;
ULL b = 37;//計算字符串的哈希值
void get_hash(string& st) {ULL hash = 0;for (auto&x:st)hash = hash * b + x;a.insert(hash);
}int main() {int n; cin >> n;string st;while (n--) {cin >> st;get_hash(st);}cout << a.size() << endl;return 0;
}

P10468 兔子與兔子 - 洛谷

P10468 兔子與兔子 - 洛谷

題目涉及頻繁的區間查詢，因此需要計算不同長度的字符串的哈希值，和不同質數次冪存儲起來，用以方便查詢。

需要注意的是，測試樣例是按照字符串首字符的下標為1進行計算的，因此計算哈希值時需要先做預處理。

之后就是通過公式Hash[i]=Hash[i-1]*P+st[i]計算哈希值（st[i]-'a'也不影響，因為字符串只有小寫字母）。

查詢時按照公式Hash[r]-Hash[l-1]*pm[r-l+1]獲取指定字符串的哈希值。

#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ULL;
ULL Hash[1000010];
ULL pm[1000010] = { 1,31 };
int P = 31;int main() {string st;cin >> st;st = '_' + st;Hash[1] = st[1] - 'a';for (size_t i = 2; i < st.size(); i++) {Hash[i] = Hash[i - 1] * P + st[i]-'a';pm[i] = pm[i - 1] * P;}int T; cin >> T;while (T--) {int l1, r1, l2, r2;cin >> l1 >> r1 >> l2 >> r2;if (r1 >= st.size() || r2 >= st.size()) {cout << "No\n";continue;}if (Hash[r1] - Hash[l1 - 1] * pm[r1 - l1 + 1] ==Hash[r2] - Hash[l2 - 1] * pm[r2 - l2 + 1])cout << "Yes\n";elsecout << "No\n";}return 0;
}

哈希沖突

對于兩個數據元素的關鍵字 $k_i$ 和 $k_j(i!=j)$，有 $k_i$ != $k_j$ ，但有：
$\text{Hash}(k_i)=\text{Hash}(k_j)$，即：不同關鍵字通過相同的哈希函數計算出相同的哈希地址，該種現象稱為哈希沖突（或哈希碰撞）。

把具有不同關鍵碼而具有相同哈希地址的數據元素稱為 “同義詞”。

引起哈希沖突的一個原因可能是：哈希函數設計不夠合理。例如直接定址法的哈希函數$\text{Hash}(\text{Key})=\text{A}\times \text{Key?+?B}$，雖然不會產生哈希沖突的問題，但占用空間會變的很大，因此個人認為哈希函數設計不合理可能是在某些方面做了犧牲導致存在哈希沖突的可能。

哈希函數設計原則

哈希函數設計原則：

1. 哈希函數的定義域必須包括需要存儲的全部關鍵碼，而如果散列表允許有m個地址時，其值域必須在0到m-1之間。

2. 哈希函數計算出來的地址能均勻分布在整個空間中。

3. 哈希函數應該比較簡單。

哈希函數設計的越精妙，產生哈希沖突的可能性就越低，但是無法避免哈希沖突。

解決哈希沖突兩種常見的方法是：閉散列和開散列。

哈希沖突解決方法—閉散列

閉散列也叫開放定址法，當發生哈希沖突時，如果哈希表未被裝滿，說明在哈希表中必然還有空位置，那么可以把 key 存放到沖突位置中的下一個空位置中去。如何尋找下一個空位是要解決的問題。

閉散列的線性探測

比如之前的除留取余法場景，現在需要插入元素44，先通過哈希函數計算哈希地址，hashAddr 為4，因此44理論上應該插在該位置，但是該位置已經放了值為4的元素，即發生哈希沖突。

于是從發生沖突的位置開始，依次向后探測（若后續空位置沒有了，則從0開始），直到尋找到下一個空位置為止。顯然在這個哈希表中找到下標為8的位置為空。這種解決哈希沖突的辦法叫線性探測。

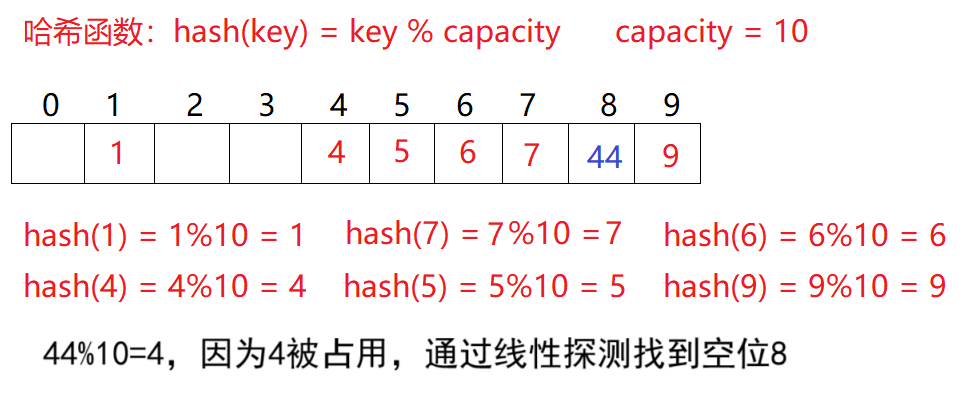
線性探測的操作：

• 插入

  • 通過哈希函數獲取待插入元素在哈希表中的位置。即獲取哈希地址。
  • 如果該位置中沒有元素則直接插入新元素。
  • 如果該位置中有元素發生哈希沖突，使用線性探測找到下一個空位置，插入新元素。只要負載因子不是1，就一定能找到。

• 刪除

  • 采用閉散列處理哈希沖突時，不能隨便物理刪除哈希表中已有的元素，若直接刪除元素會影響其他元素的搜索。

    比如刪除元素4，如果直接刪除掉，44查找起來可能會受影響。因此線性探測采用標記的偽刪除法來刪除一個元素。這種偽刪除法在棧的c語言實現 - CSDN博客中有提到，但棧是通過棧頂指針來控制元素是否被刪除，在哈希表的話需要用其他標志（比如enum定義3個枚舉常量表示狀態）來記錄。

• 擴容

  哈希表的擴容和載荷因子有關。

  散列表的載荷因子（有的資料稱負載因子，它們都是同一概念的中文翻譯）定義為：
  $\alpha$ = 填入表中的元素個數 $÷$ 散列表的長度

  $\alpha$ 是散列表裝滿程度的標志因子。由于表長是定值，$\alpha$ 與“填入表中的元素個數”成正比。

  所以，$\alpha$ 越大，表明填入表中的元素越多，產生沖突的可能性就越大；
  反之，$\alpha$ 越小，標明填入表中的元素越少，產生沖突的可能性就越小。

  實際上，散列表的平均查找長度是載荷因子的函數，只是不同處理沖突的方法有不同的函數。

對于開放定址法，荷載因子是特別重要因素，應嚴格限制在0.7或0.8以下。超過0.8，查表時的CPU緩存不命中（cache missing）按照指數曲線上升。因此，一些采用開放定址法的 hash 庫，如 Java 的系統庫限制了荷載因子為0.75，超過此值將resize（擴容）散列表。

研究表明：當表的長度為質數且表裝載因子 $\alpha$ 不超過0.5時，新的表項一定能夠插入，而且任何一個位置都不會被探查兩次。因此只要表中有一半的空位置，就不會存在表滿的問題。在搜索時可以不考慮表裝滿的情況，但在插入時必須確保表的裝載因子 $\alpha$ 不超過0.5**，**如果超出必須考慮增容。

ASL（Average Search Length），即平均查找長度，用于衡量散列表的效率的屬性。在查找成功的情況下，
$AS{L}_{成功}=\frac{\sum 查找次數}{元素個數}$。其中每個元素的查找次數為從計算出的哈希地址開始比較，到找到當前數據總共的比較次數。$\frac{1}{元素個數}$也可以叫查找概率，或每個關鍵字的權重。

查找失敗的前提是查找到空位置，例如映射到下標1的元素，需要查找到空位2才算查找失敗，所以需要查找1次才能確定查找失敗。而空位置同樣需要做至少1次比較，所以查找次數為1次。

$AS{L}_{失敗}=\frac{\sum 查找次數}{p}$，$p$是除留取余法的模數，也可以是空間大小。

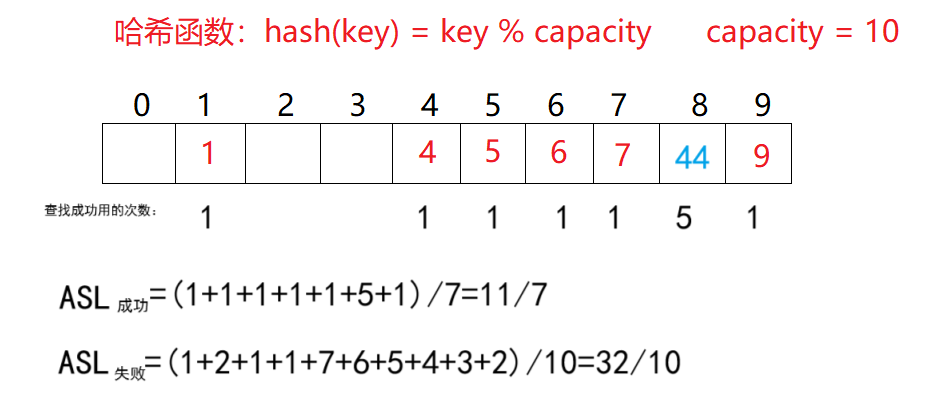
線性探測優點是實現非常簡單，缺點也很明顯，一旦發生哈希沖突，所有的沖突連在一起，容易產生數據“堆積”，即：不同關鍵碼占據了可利用的空位置，使得尋找某關鍵碼的位置需要許多次比較，導致搜索效率降低。

閉散列的二次探測

線性探測的缺陷是產生沖突的數據堆積在一塊，這與其找下一個空位置的方法有關系，因為找空位置的方式就是挨著往后逐個去找。

因此二次探測為了避免該問題，找下一個空位置的方法為按照$+1^2,?1^2,+2^2,?2^2,\dots$的順序進行探測，具體按照函數$H_i=(H_0+i^2)\%m$, 或者：$H_i=(H_0?i^2)\%m$去查找。其中：$i=1,2,3,\dots$。

但二次探測意味著走更大的步長，盡管比起一次探測減少了沖突聚集和同負載因子下沖突概率低于一次探測，但仍然會帶來二次聚集（即哈希沖突造成的聚集依舊會出現，只是出現得更晚）。

且步長增加可能導致無法找到空位，且負載因子越大，因為找不到空位陷入死循環的風險越高。有研究證明，哈希表的表長為$4k+3(k\in N^{?})$的素數時一定可以探測到，詳細證明見開放定址法——平方探測(Quadratic Probing) - 儀式黑刃 - 博客園。

閉散列無論是哪種探測，對哈希表的每個位置都要設置3種狀態例如EMPTY、DELETE、EXIST。默認情況表是EMPTY，有數據插入時修改為EXIST，刪除數據時修改為DELETE。這樣做是為了避免刪除數據后造成EMPTY位影響查找。

綜上，無論是線性探測還是二次探測，閉散列最大的缺陷就是空間利用率比較低，這同樣也是哈希的缺陷。但閉散列也并非不能用，在數據量小但操作頻率高的場景，閉散列的性能也略優于其他解決方法（回憶交換排序——快速排序3 針對LeetCode某OJ的優化-CSDN博客中的小區間優化）。

哈希沖突解決方法—開散列

開散列是哈希的學習重點。

開散列概念

開散列法又叫鏈地址法（開鏈法、拉鏈法），首先對關鍵碼集合用散列函數計算散列地址，具有相同地址的關鍵碼歸于同一子集合，每一個子集合稱為一個桶，各個桶中的元素通過一個（單）鏈表鏈接起來，各鏈表的頭結點存儲在哈希表中。對這個抽象出來的桶有的資料稱哈希桶。

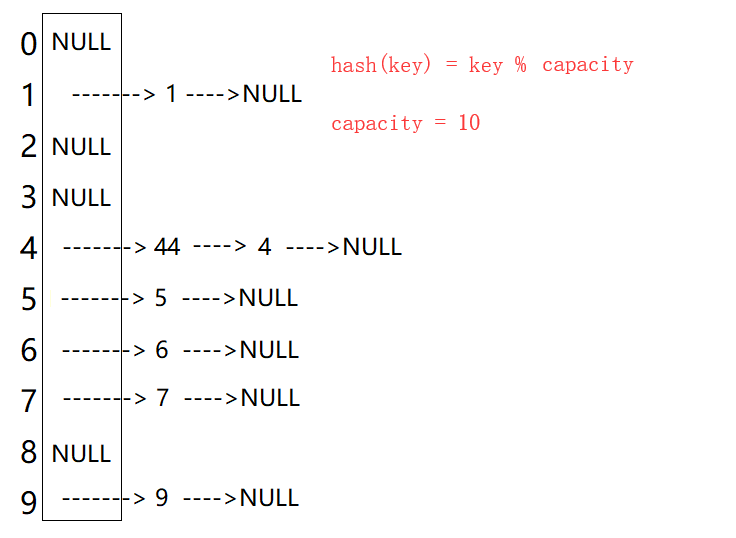
從上圖可以看出，開散列中每個桶中放的都是發生哈希沖突的元素。

開散列增容

桶的個數是固定的，隨著元素的不斷插入，每個桶中元素的個數不斷增多，極端情況下，可能會導致一個桶中鏈表節點非常多，會影響的哈希表的性能。

主流的解決方法有二：

• 鏈表換成紅黑樹。
• 對哈希表進行增容。

而且很多時候都是 2 個解決方法一起使用。

開散列最好的情況是：每個哈希桶中剛好掛一個節點，再繼續插入元素時，每一次都會發生哈希沖突，因此，在元素個數剛好等于桶的個數時，可以給哈希表增容。

ASL對開散列同樣適用。但其中空指針的查找失敗的情況有的資料算作0，而有的算作1。

開散列與閉散列比較：

應用鏈地址法處理溢出，需要增設鏈接指針，似乎增加了存儲開銷。事實上：由于開放定址法必須保持大量的空閑空間以確保搜索效率，如二次探查法要求裝載因子$a\le 0.7$，而表項所占空間又比指針大的多，所以使用鏈地址法反而比開地址法節省存儲空間。

哈希算法的時間復雜度計算

哈希表的時間復雜度主要取決于哈希函數質量、沖突解決策略、負載因子（Load Factor） 等因素，因此只能做大致估算。

在開散列中，可通過平均查找長度（ASL - Average Search Length）來確定。即找每個元素需要查找的次數加起來，除以總的元素個數，結果的數量級即為時間復雜度。

在閉散列中，查找任何元素都有可能進行若干次一次探測或二次探測，不同的數據集合可能造成探測的平均次數不同，比起開散列更難估計。

但無論如何，哈希的平均復雜度是$O(1)$。但在開散列中，某個哈希桶的長度太長會降低哈希表的性能，有的工具為解決這個問題，會將哈希桶也設置成紅黑樹。

哈希的應用

c++STL-unordered系列

unordered系列工具指unordered_map、unordered_multimap、unordered_set、unordered_multiset，這些工具都是在C++11標準中添加，使用它們需要編譯器支持C++11。詳細參考 - C++ Reference。

//unordered_set
template < class Key, // unordered_set::key_type/value_typeclass Hash = hash<Key>,//unordered_set::hasherclass Pred = equal_to<Key>, //unordered_set::key_equalclass Alloc = allocator<Key>//unordered_set::allocator_type> class unordered_set;
//unordered_set
template < class Key,//unordered_multiset::key_type/value_typeclass Hash = hash<Key>,class Pred = equal_to<Key>,class Alloc = allocator<Key>> class unordered_set;
//unordered_map
template < class Key,class T,class Hash = hash<Key>,class Pred = equal_to<Key>,class Alloc = allocator< pair<const Key,T> >> class unordered_map;
//unordered_multimap
template < class Key,class T,class Hash = hash<Key>,class Pred = equal_to<Key>,class Alloc = allocator< pair<const Key,T> >> class unordered_multimap;

嚴格來說，之前的map、set是通過紅黑樹實現的，而unordered系列則是通過哈希表實現的。

STL設計開始的時候，可能因為調研等各種原因（自己猜測），沒考慮引入哈希，而是直接設計了紅黑樹為基礎的map和set，這就導致后期引入哈希的map和哈希的set時不能用原來的名字，于是就改用unordered。

unordered中文翻譯大致為無序，可能是想暗示存儲方式是無序的（紅黑樹通過中序遍歷得到的數據也是有序的序列）。

但這些歷史的工具，我們僅需學習即可。而且它們的使用和map和set在絕大部分場合無區別。

這些工具和map、set的使用方法幾乎一致，詳細見c++STL-map和set的模擬實現-CSDN博客。這里挑重點講。

紅黑樹和哈希表的插入特點

紅黑樹因為二叉搜索樹的特性，插入其中的數據再遍歷時是有序的，但哈希表無序。

#include<set>
#include<unordered_set>
#include<vector>
#include<iostream>
using namespace std;template<class T>
void print(T& c) {for (auto& x : c)cout << x << ' ';cout << endl;
}template<class T>
void Insert(T& c) {vector<int>a = { 11,4,18,61,19,5,68,64 };for (auto& x : a)c.insert(x);
}int main() {set<int>tree;unordered_set<int>ht;Insert(tree);print(tree);Insert(ht);print(ht);return 0;
}

在MSVC編譯器（IDE是VS2019）運行結果：

4 5 11 18 19 61 64 68
19 11 68 4 18 5 61 64

在g++編譯器（IDE是Dev-c++ 5.11）運行結果：

4 5 11 18 19 61 64 68
64 68 5 19 61 18 4 11

在2個編譯器下，同一代碼的輸出不同的根本原因是不同編譯器對底層哈希表的實現方式不同，包括哈希函數設計、哈希沖突解決策略、擴容機制等。這里不過多細究。

紅黑樹和哈希表的效率對比

首先是無序，且重復較少的情況。

#include<set>
#include<unordered_set>
#include<vector>
#include<iostream>
#include<ctime>
using namespace std;
vector<int>nums(100000);template<class T>
size_t Insert(T& c) {size_t start = 0, finish = 0;//測試插入start = clock();for (auto& x : nums)c.insert(x);finish = clock();return finish - start;
}template<class T>
size_t Find(T& c) {size_t start = 0, finish = 0;//測試插入auto ans = c.find(*c.begin());start = clock();for (auto& x : nums)ans = c.find(x);finish = clock();return finish - start;
}template<class T>
size_t Erase(T& c) {size_t start = 0, finish = 0;//測試插入start = clock();for (auto& x : nums)c.erase(x);finish = clock();return finish - start;
}int main() {srand(size_t(time(0)));for (size_t i = 0; i < nums.size(); i++)nums[i] = rand() * rand();set<int>tree;unordered_set<int>ht;cout << "set insert: " << Insert(tree) << endl;cout << "unordered_set insert: " << Insert(ht) << endl;cout << "set 成功插入數量：" << tree.size() << endl;cout << "unordered_set 成功插入數量：" << ht.size() << endl;cout << "set find: " << Find(tree) << endl;cout << "unordered_set find: " << Find(ht) << endl;cout << "set erase: " << Erase(tree) << endl;cout << "unordered_set erase: " << Erase(ht) << endl;return 0;
}

輸出結果之一（VS2019，32位，Debug模式）：

set insert: 249
unordered_set insert: 185
set 成功插入數量：99948
unordered_set 成功插入數量：99948
set find: 155
unordered_set find: 68
set erase: 259
unordered_set erase: 56

然后是有序的情況。

int main() {for (size_t i = 0; i < nums.size(); i++)nums[i] = i;set<int>tree;unordered_set<int>ht;cout << "set insert: " << Insert(tree) << endl;cout << "unordered_set insert: " << Insert(ht) << endl;cout << "set 成功插入數量：" << tree.size() << endl;cout << "unordered_set 成功插入數量：" << ht.size() << endl;cout << "set find: " << Find(tree) << endl;cout << "unordered_set find: " << Find(ht) << endl;cout << "set erase: " << Erase(tree) << endl;cout << "unordered_set erase: " << Erase(ht) << endl;return 0;
}

輸出結果之一（VS2019，32位，Debug模式）：

set insert: 273
unordered_set insert: 175
set 成功插入數量：100000
unordered_set 成功插入數量：100000
set find: 129
unordered_set find: 62
set erase: 208
unordered_set erase: 52

更極端的情況：

int main() {for (size_t i = 0; i < nums.size() / 2; i++)nums[i] = 666;for (size_t i = nums.size() / 2; i < nums.size(); i++)nums[i] = 999;set<int>tree;unordered_set<int>ht;cout << "set insert: " << Insert(tree) << endl;cout << "unordered_set insert: " << Insert(ht) << endl;cout << "set 成功插入數量：" << tree.size() << endl;cout << "unordered_set 成功插入數量：" << ht.size() << endl;cout << "set find: " << Find(tree) << endl;cout << "unordered_set find: " << Find(ht) << endl;cout << "set erase: " << Erase(tree) << endl;cout << "unordered_set erase: " << Erase(ht) << endl;return 0;
}

輸出結果之一（VS2019，32位，Debug模式）：

set insert: 62
unordered_set insert: 55
set 成功插入數量：2
unordered_set 成功插入數量：2
set find: 43
unordered_set find: 56
set erase: 42
unordered_set erase: 10

這里差距不明顯的原因是VS2019的哈希表的底層實現有用紅黑樹優化。若使用單鏈表，或其他哈希函數則可能做不到這種優勢。

但可以肯定的是，在有序的情況下，紅黑樹比哈希表有優勢，因為紅黑樹的平衡調節機制能避免直接比較所有函數。

但數據無序時，很多時候看上去是哈希表對紅黑樹的全面碾壓。

哈希表特有的成員函數

unordered_map、unordered_set、unordered_multimap、unordered_multiset都有的：

//Buckets
size_type bucket_count() const noexcept;
size_type max_bucket_count() const noexcept;
size_type bucket_size ( size_type n ) const;
size_type bucket ( const key_type& k ) const;
//Hash policy
float load_factor() const noexcept;
float max_load_factor() const noexcept;
void max_load_factor ( float z );
void rehash ( size_type n );
void reserve ( size_type n );
//Observers
hasher hash_function() const;//hasher是第3個模板參數
key_equal key_eq() const;
allocator_type get_allocator() const noexcept;

bucket_count：返回當前哈希表中桶（bucket）的數量。

max_bucket_count()：返回哈希表能支持的最大桶數（由系統和實現限制）。

bucket_size( size_type n )：返回第 n 個桶中的元素數量。

bucket ( const key_type& k )：返回鍵 k 所在的桶的索引。

load_factor：返回當前負載因子，即 $\frac{元素數量}{桶數量}$。

float max_load_factor()：返回哈希表的最大允許負載因子（默認通常為 1.0）。

void max_load_factor：設置最大負載因子為 z。z 為正數，建議在 0.1 ~ 1.0 之間。

rehash( size_type n )：將桶數量調整為至少 n，并重新哈希所有元素。

reserve( size_type n )：預留至少能容納 n 個元素的桶空間。

hash_function：返回哈希表使用的哈希函數對象。

key_eq：返回哈希表使用的鍵比較函數對象（默認是 std::equal_to<key_type>）。

get_allocator：返回哈希表的內存分配器。

noexcept關鍵字會使函數不會拋出異常，主要用于優化函數性能。若使用了noexcept關鍵字修飾函數，但函數依舊拋出了異常，則程序會調用std::terminate強行終止程序（斷言）。

學習了這么多容器，相信這些函數看一眼就知道怎么玩，就不給使用示例了。

可能有關的OJ

961. 在長度 2N 的數組中找出重復 N 次的元素 - 力扣

961. 在長度 2N 的數組中找出重復 N 次的元素 - 力扣（LeetCode）

class Solution {
public:int repeatedNTimes(vector<int>& nums) {unordered_map<int,int>hash;for(auto&x:nums)hash[x]++;for(auto&x:hash)if(x.second>1)return x.first;return 0;}
};

350. 兩個數組的交集 II - 力扣

350. 兩個數組的交集 II - 力扣（LeetCode）

class Solution {
public:vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {sort(nums1.begin(),nums1.end());sort(nums2.begin(),nums2.end());int p1=0,p2=0;vector<int>ans;while(p1<nums1.size()&&p2<nums2.size()){if(nums1[p1]<nums2[p2])++p1;else if(nums1[p1]>nums2[p2])++p2;else{ans.push_back(nums1[p1++]);p2++;}}return ans;}
};

217. 存在重復元素 - 力扣

217. 存在重復元素 - 力扣（LeetCode）

class Solution {
public:bool containsDuplicate(vector<int>& nums) {unordered_map<int,int>mp;for(auto&x:nums)mp[x]++;for(auto&x:mp)if(x.second>1)return true;return false;}
};

884. 兩句話中的不常見單詞 - 力扣

884. 兩句話中的不常見單詞 - 力扣（LeetCode）

class Solution {
public:vector<string> uncommonFromSentences(string s1, string s2) {unordered_map<string,int>mp;vector<string>ans;size_t p=0;for(size_t i=s1.find(" ",0);i!=-1;i=s1.find(" ",i+1)){mp[s1.substr(p,i-p)]++;p=i+1;}if(p<s1.size())mp[s1.substr(p)]++;p=0;for(size_t i=s2.find(" ",0);i!=-1;i=s2.find(" ",i+1)){mp[s2.substr(p,i-p)]++;p=i+1;}if(p<s2.size())mp[s2.substr(p)]++;for(auto&x:mp)if(x.second==1)ans.push_back(x.first);return ans;}
};

位圖bitset

面試題（背景）：給40億個不重復的無符號整數，沒排過序。給一個無符號整數，如何快速判斷一個數是否在這40億個數中。【騰訊】

方法：

1. 遍歷，時間復雜度$O(N)$。首先排除。

2. 排序（$O(N\log N)$)，利用二分查找: $\log N$。

   理論查找次數：${\log }_{2}4\times 10^9\approx 9{\log }_{2}10\approx 32$，即最多查找32次。

   現在的問題是，內存中沒有這么多的空間存儲這么多數，更不用說對這么多數進行排序。

3. 位圖解決。

數據是否在給定的整形數據中，結果是在或者不在，剛好是兩種狀態，那么可以使用一個二進制比特位來代表數據是否存在的信息，如果二進制比特位為1，代表存在，為0代表不存在。比如小端存儲的設備：

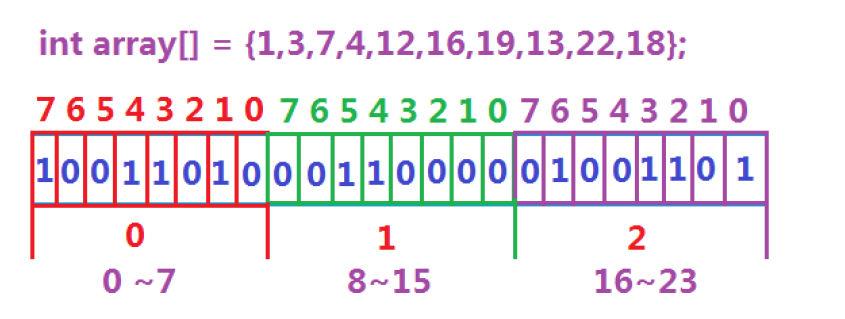
所謂位圖，就是用每一位 bit 位來存放某種狀態，適用于海量數據，數據無重復的場景。通常是用來判斷某個數據存不存在的。位圖實質上是直接定址法的哈希，在STL中也有對應的工具，屬于位序列容器，詳見bitset - C++ Reference。

但這個bitset的底層是靜態數組，在編譯時確認容量，因此bitset是直接在棧上分配內存，在函數內部申請棧空間不夠用，推薦放全局使用。

位圖的應用：

1. 快速查找某個數據是否在一個集合中。

2. 排序 + 去重。

3. 求兩個集合的交集、并集等。

4. 操作系統中磁盤塊標記。

構造函數

bitset();
bitset (unsigned long val);
template<class charT, class traits, class Alloc>explicit bitset (const basic_string<charT,traits,Alloc>& str,typename basic_string<charT,traits,Alloc>::size_type pos = 0,typename basic_string<charT,traits,Alloc>::size_type n =basic_string<charT,traits,Alloc>::npos);

第3個構造函數：

basic_string實際就是標準庫里的string，這里寫全是因為這個位圖可能使用wstring或其他的。

剩下的3個形參就是從下標0開始的n和字符。

#include <iostream>
//使用STL的位圖需要展開頭文件
#include <bitset>
using namespace std;int main() {bitset<8>bt1(0xaa);bitset<8>bt2(0xBB);bitset<8>bt3("10101010");//需要指出用的是哪個basic_stringbitset<8>bt4(string("10111100"), 3, 3);bitset<8>bt5;//bitset<8>bt6("g8sad41");//字符串只能包含0和1，否則會產生未定義行為//位圖有重載operator<<cout << bt1 << endl;cout << bt2 << endl;cout << bt3 << endl;cout << bt4 << endl;cout << bt5 << endl;return 0;
}

輸出：

10101010
10111011
10101010
00000111
00000000

位圖支持幾乎所有的關系運算符。

//member functions	成員函數
bitset& operator&= (const bitset& rhs);
bitset& operator|= (const bitset& rhs);
bitset& operator^= (const bitset& rhs);
bitset& operator<<= (size_t pos);
bitset& operator>>= (size_t pos);
bitset operator~() const;
bitset operator<<(size_t pos) const;
bitset operator>>(size_t pos) const;
bool operator== (const bitset& rhs) const;
bool operator!= (const bitset& rhs) const;//non-member functions	 非成員函數
template<size_t N>
bitset<N> operator& (const bitset<N>& lhs, const bitset<N>& rhs);
template<size_t N>
bitset<N> operator| (const bitset<N>& lhs, const bitset<N>& rhs);
template<size_t N>
bitset<N> operator^ (const bitset<N>& lhs, const bitset<N>& rhs);//iostream inserters/extractors 支持流插入和流提取的關鍵	
template<class charT, class traits, size_t N>
basic_istream<charT, traits>&
operator>> (basic_istream<charT,traits>& is, bitset<N>& rhs);
template<class charT, class traits, size_t N>
basic_ostream<charT, traits>&
operator<< (basic_ostream<charT,traits>& os, const bitset<N>& rhs);

函數接口Bit access

     bool operator[] (size_t pos) const;
reference operator[] (size_t pos);
size_t count() const;
size_t size() const;
bool test (size_t pos) const;
bool any() const;
bool none() const;
bool all() const noexcept;//需要編譯器支持c++11

[]：返回第pos位的值，不檢查越界，即給的值超過初始化范圍會造成越界訪問，行為未定義。reference是引用，也就是說位圖支持下標修改。

test：返回第pos位的值，會檢查越界，若越界會拋出異常std::out_of_range。和[]功能有重疊。

count：返回存儲的1的總位數。

size：返回模板參數N即總位數。

any：檢查位圖是否至少有1個1。

none：檢查是否全為0。

all：檢查是否全為1。

#include <iostream>
#include <bitset>
using namespace std;int main() {try {bitset<32>bt;cout << bt.size() << endl;cout << bt.none() << endl;bt[3] = 1;cout << bt.test(3) << endl;cout << bt.count() << endl;cout << bt.any() << endl;cout << bt.all() << endl;bt = 0xffffffff;//賦值unsigned(-1)cout << bt.all() << endl;//bt[34] = 1;//越界訪問且不會被異常捕獲auto nn=bt.test(34);//越界訪問且會被異常捕獲}catch (const exception& e) {cout << e.what() << endl;}return 0;
}

比特位操作Bit operations

bitset& set();
bitset& set (size_t pos, bool val = true);
bitset& reset();
bitset& reset (size_t pos);
bitset& flip();
bitset& flip (size_t pos);
template <class charT, class traits, class Alloc>basic_string<charT,traits,Alloc> to_string() const;
unsigned long to_ulong() const;
unsigned long long to_ullong() const;

set：啥參數都不給就全變1，給參數就變指定位為val。

reset：啥參數都不給就全變0，給參數就變指定位為0。

flip：啥都不給時將所有位取反，否則就將第pos位取反。

剩下的to_string是根據位圖存儲的數據返回字符串，to_ulong是返回unsigned long，to_ullong是返回unsigned long long型整數。

模擬實現位圖

回顧之前的問題：給40億個不重復的無符號整數，沒排過序。給一個無符號整數，如何快速判斷一個數是否在這40億個數中。【騰訊】

在c語言中，一個int有32個bit位，存儲N個數，開N/32+1個int的空間即可滿足存儲這么多數據在與不在的信息。

所以40億個整數需要42億+的比特位（方便計算），約為1 3421 7728個int型變量的數組，換算成內存是 0.5 GB，內存可以容納。若是用bitset，則需要將bitset放在全局，函數內部無法存放這么多的數據。

位圖的底層可以用vector<int>代替，即動態數組。因此可以自己設計一個位圖。

位圖的操作可以先設計3個函數：

1. set函數。
2. reset函數。
3. test函數。

也可以加別的函數，這里設計3個就足夠解決絕大部分大數據查找問題。

操縱 bit 位最常用的方式是通過1左移多少位來操作。左移指在內存中將所有1往高位移，無論是大端還是小端存儲。例如想讓第4個 bit 位變成1：

void f(int& aim){aim|=(1<<4);
}

即1先左移4位，再和aim進行或運算，因為1<<4轉換成int后其他位全是0，與aim進行或運算，除了指定 bit 位，其他位不受影響。

模擬實現參考：

namespace mystd {// N是需要多少比特位template<size_t N>class bitset {public:bitset() {_bits.resize(N/32+1, 0);//_bits.resize((N>>5) + 1, 0);//可以使用位運算計算需要多少空間 }void set(size_t x) {//將bit位設置為1 size_t i = x / 32;//查找數據在第幾個整型 size_t j = x % 32;//查找數據在一個整型中的第幾位 _bits[i] |= (1 << j);}void reset(size_t x) {//將bit位設置成0 size_t i = x / 32;size_t j = x % 32;_bits[i] &= ~(1 << j);//1左移多少位，再按位取反，和指定整數做與運算 }bool test(size_t x) {//查詢指定數據是否存在 size_t i = x / 32;size_t j = x % 32;return _bits[i] & (1<<j);//查詢指定bit位是否為1}private:vector<int> _bits;};
}

位圖實戰：

1. 給定100億個整數，設計算法找到只出現一次的整數？問題變形：1個文件有100億個int，1G內存，設計算法找到出現次數不超過2次的所有整數。

   首先這個整數的大小有限，最多42億。每個位圖只能表示數是否存在，根據二進制的原理，2個位圖即可用2個 bit 位來統計每個數的出現次數，找出只出現1次的整數完全足夠，所以可以用2個位圖表示每個數的出現次數。

   參考程序：

#pragma once
#include<iostream>
using std::cout;
using std::endl;namespace mystd {// N是需要多少比特位template<size_t N>class bitset {public:bitset() {_bits.resize(N/32+1, 0);//_bits.resize((N>>5) + 1, 0);//可以使用位運算計算需要多少空間 }void set(size_t x) {//將bit位設置為1 size_t i = x / 32;//查找數據在第幾個整型 size_t j = x % 32;//查找數據在一個整型中的第幾位 _bits[i] |= (1 << j);}void reset(size_t x) {//將bit位設置成0 size_t i = x / 32;size_t j = x % 32;_bits[i] &= ~(1 << j);//1左移多少位，再按位取反，和指定整數做與運算 }bool test(size_t x) {//查詢指定數據是否存在 size_t i = x / 32;size_t j = x % 32;return _bits[i] & (1<<j);//查詢指定bit位是否為1}private:vector<int> _bits;};//將2個位圖進行封裝，統計每個數的出現次數 template<size_t N>class twobitset {public:void set(size_t x) {//00表示之前沒出現過，現在出現了，需要記錄01 if (_bs1.test(x) == false && _bs2.test(x) == false)_bs2.set(x);//01表示之前出現過1次，現在出現第2次 else if (_bs1.test(x) == false && _bs2.test(x) == true) {_bs1.set(x);_bs2.reset(x);}//10表示之前已經出現2次，這是第3次出現 else if (_bs1.test(x) == true && _bs2.test(x) == false) {_bs1.set(x);_bs2.set(x);}}void Print() {for (size_t i = 0; i < N; i++)//只出現過1次的數 if (_bs1.test(i) == false && _bs2.test(i) == true)cout <<"1->" << i << endl;//出現過2次的數 else if (_bs1.test(i) == true && _bs2.test(i) == false)cout <<"2->" << i << endl;cout << endl;}private:bitset<N> _bs1;//每個值占用2個位圖中的2個位。 bitset<N> _bs2;};
}

2. 給兩個文件，分別有100億個整數，我們只有1G內存，如何找到兩個文件交集？

   2個文件的數各自映射在2個位圖上，逐位比較是否同時為1即可。這里就不再給具體實現。

梳理迄今為止學過的搜索：

1. 暴力查找，數據量大時效率低。
2. 排序 + 二分，問題：(1)排序有代價，特別是空間資源方面(2)不方便增刪
3. 搜索樹 -> AVL樹和紅黑樹。很穩定，也比常規的數組、鏈表快，但還不夠快。
4. 哈希，雖然確實很快，但極端場景下效率會下降，例如某個哈希函數值映射有很多個數據。

若處理整型的在與不在問題：使用位圖以及變形，相比與上文節省空間。非整型也可通過哈希函數抓換成整型，也可以使用布隆過濾器。

布隆過濾器

我們在使用新聞客戶端看新聞時，它會給我們不停地推薦新的內容，它每次推薦時要去重，去掉那些已經看過的內容。

新聞客戶端推薦系統用服務器記錄了用戶看過的所有歷史記錄，當推薦系統推薦新聞時會從每個用戶的歷史記錄里進行篩選，過濾掉那些已經存在的記錄，用這種方式實現推送去重。

如何快速查找呢？

1. 用哈希表存儲用戶記錄，缺點：浪費空間。

2. 用位圖存儲用戶記錄，缺點：位圖一般只能處理整形，如果內容編號是字符串，就無法處理了。無法處理指多個不同的字符串，轉換為哈希值映射到位圖上的位置一樣，這會導致判斷字符串在不在集合中時容易出現誤判（指之前已有哈希值占據了某個位置，后來不在的字符串根據這個位置的0、1狀態來判斷在與不在）。

   

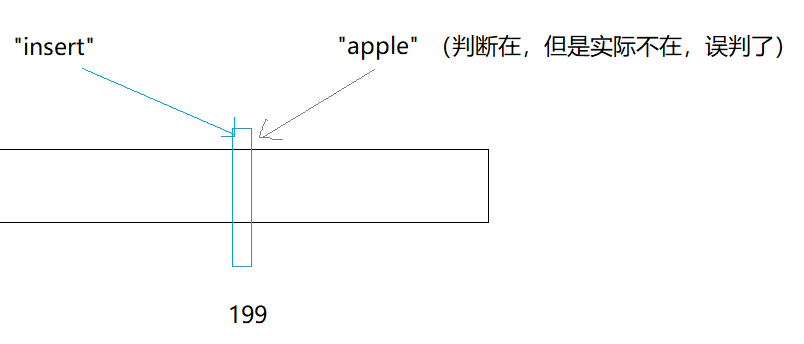
3. 將哈希與位圖結合，即布隆過濾器。

布隆過濾器是由布隆（Burton Howard Bloom）在1970年提出的一種數據結構，特點是高效地插入和查詢，可以用來告訴你 “某樣東西一定不存在或者可能存在”，它是用多個哈希函數，將一個數據映射到位圖結構中。此種方式不僅可以提升查詢效率，也可以節省大量的內存空間。例如下圖$x$就通過 3 種哈希函數映射到第2、第6和第14個bit位。

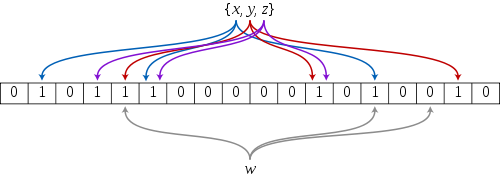
布隆過濾器查找$w$是否存在于集合中，也只需通過這3種哈希函數計算哈希地址即可。

詳解布隆過濾器的原理，使用場景和注意事項 - 知乎

布隆過濾器的查找

布隆過濾器的思想是將一個元素用多個哈希函數映射到一個位圖中，因此被映射到的位置的比特位一定為1。

所以可以按照以下方式進行查找：分別計算每個哈希值對應的比特位置存儲的是否為零，只要有一個為零，代表該元素一定不在哈希表中，否則可能在哈希表中。

注意：布隆過濾器判斷某個元素不存在時，該元素一定不存在；判斷該元素存在時，該元素可能存在，因為有些哈希函數存在一定的誤判，多個哈希函數只能做到降低誤判的概率。

比如：在布隆過濾器中查找"alibaba"時，假設3個哈希函數計算的哈希值為：1、3、7，剛好和其他元素的比特位重疊，此時布隆過濾器告訴該元素存在，但實該元素是不存在的。

布隆過濾器的使用場景需要能接受誤判。例如在網頁上注冊時，想判斷一個昵稱是否被用過，沒有用過則提示沒用過。這時可以將服務器中的昵稱都放在布隆過濾器中，無論某個昵稱是否被誤判，對用戶來說都能 ”接受“ ，反正更換一個昵稱的事。

服務器溫度較高時，發生火災的概率相對較低，真正嚴重的問題是熱衰減。熱衰減問題是個常見的現象，手機溫度過高時打游戲會掉幀，電腦溫度過高時可能會卡。

為了避免熱衰減，很多公司將服務器建在貴州省的大山中，把山挖空后服務器放里面。這就不得不避免數據需要經過很多中介轉換，因此布隆過濾器等能快速確定某個數據在與不在的工具應用十分廣泛。

在數據庫中，用戶刻意將名稱弄成很長的字節，這時查找字符串在不在時，數據庫比較字符串時需要一個一個ascll碼去比。為了解決這個問題，就在數據庫中多建一個哈希列，將已存有的昵稱轉換成哈希值。之后再查找時先比較哈希值，相等的話再查找是否在不在。通過哈希值查找本身就相當于過濾。

同樣的場景還有：若數據存放在多臺服務器中的一臺，這時需要通過某種哈希查找數據在哪一臺，然后在那一臺仔細搜查即可。

哈希還有一致性哈希。因為服務器增加類比到哈希中的概念就是擴容，一臺服務器內的數據特別龐大，將它們全部通過哈希函數進行二次計算不現實，因此在原來的哈希的基礎上還有一致性哈希。還有負載均衡：很多人來連接同一臺服務器，服務器該如何處理。

布隆過濾器刪除

布隆過濾器不能直接支持刪除工作，因為在刪除一個元素時，可能會影響其他元素。

比如：刪除上圖中"tencent"元素，如果直接將該元素所對應的二進制比特位變成0，“baidu”元素也被刪除了，因為這兩個元素在多個哈希函數計算出的比特位上剛好有重疊。

一種支持刪除的方法：引用計數。即將布隆過濾器中的每個比特位擴展成一個小的計數器，插入元素時給k個計數器（k個哈希函數計算出的哈希地址）加 1 ，刪除元素時，給k個計數器減 1 ，通過多占用幾倍存儲空間的代價來增加刪除操作。

布隆過濾器優點和缺陷

優點：

1. 增加和查詢元素的時間復雜度為:$O(K)$, ($K$為哈希函數的個數，一般比較小)，與數據量大小無關。

2. 哈希函數相互之間沒有關系，方便硬件并行運算。

3. 布隆過濾器不需要存儲元素本身，在某些對保密要求比較嚴格的場合有很大優勢。

4. 在能夠承受一定的誤判時，布隆過濾器比其他數據結構有這很大的空間優勢。

5. 數據量很大時，布隆過濾器可以表示全集，其他數據結構不能。

6. 使用同一組散列函數的布隆過濾器可以進行交、并、差運算。

布隆過濾器缺陷

1. 有誤判率，即存在假陽性(False Position)，即不能準確判斷元素是否在集合中（補救方法：再建立一個白名單，存儲可能會誤判的數據）。

2. 不能獲取元素本身。

3. 一般情況下不能從布隆過濾器中刪除元素。

4. 如果采用計數方式刪除，可能會存在計數回繞問題。

布隆過濾器的模擬實現

哈希函數的選擇參考：各種字符串Hash函數 - clq - 博客園

參考：

#pragma once
#include<string>
#include<iostream>
#include<vector>
#include<cstdlib>
using std::vector;
using std::string;
using std::cout;
using std::endl;namespace mystd {//自制位圖，庫里的位圖底層為靜態數組不適合開大量空間template<size_t N>class bitset {public:bitset() {_bits.resize(N / 32 + 1, 0);//_bits.resize((N>>5) + 1, 0);//可以使用位運算計算需要多少空間 }void set(size_t x) {//將bit位設置為1 size_t i = x / 32;//查找數據在第幾個整型 size_t j = x % 32;//查找數據在一個整型中的第幾位 _bits[i] |= (1 << j);}void reset(size_t x) {//將bit位設置成0 size_t i = x / 32;size_t j = x % 32;_bits[i] &= ~(1 << j);//1左移多少位，再按位取反，和指定整數做與運算 }bool test(size_t x) {//查詢指定數據是否存在 size_t i = x / 32;size_t j = x % 32;return _bits[i] & (1 << j);//查詢指定bit位是否為1}private:vector<int> _bits;};struct BKDRHash {size_t operator()(const string& key) {// BKDRsize_t hash = 0;for (auto e : key){hash *= 31;hash += e;}return hash;}};struct APHash{size_t operator()(const string& key){size_t hash = 0;for (size_t i = 0; i < key.size(); i++){char ch = key[i];if ((i & 1) == 0){hash ^= ((hash << 7) ^ ch ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));}}return hash;}};struct DJBHash{size_t operator()(const string& key){size_t hash = 5381;for (auto ch : key){hash += (hash << 5) + ch;}return hash;}};//布隆過濾器template<size_t N,class K = string,class HashFunc1 = BKDRHash,class HashFunc2 = APHash,class HashFunc3 = DJBHash>class BloomFilter {public:void Set(const K& key) {size_t hash1 = HashFunc1()(key) % N;size_t hash2 = HashFunc2()(key) % N;size_t hash3 = HashFunc3()(key) % N;_bs.set(hash1);_bs.set(hash2);_bs.set(hash3);}// 一般不支持刪除//void Reset(const K& key);bool Test(const K& key) {// 判斷不存在是準確的size_t hash1 = HashFunc1()(key) % N;if (_bs.test(hash1) == false)return false;size_t hash2 = HashFunc2()(key) % N;if (_bs.test(hash2) == false)return false;size_t hash3 = HashFunc3()(key) % N;if (_bs.test(hash3) == false)return false;// 存在誤判的return true;}private:mystd::bitset<N> _bs;};void fbf1() {BloomFilter<100> bf;bf.Set("柯南");bf.Set("步美");bf.Set("光彥");bf.Set("胖虎");cout << bf.Test("柯南") << endl;cout << bf.Test("步美") << endl;cout << bf.Test("光彥") << endl;cout << bf.Test("小夫") << endl;cout << bf.Test("胖虎1") << endl;cout << bf.Test("胖虎2") << endl;cout << bf.Test("胖虎 ") << endl;cout << bf.Test("沉睡的小五郎") << endl;}void fbf2() {srand(size_t(time(0)));const size_t N = 10000;//可以通過增大空間的方式降低誤判率 BloomFilter<N * 100> bf;std::vector<std::string> v1;std::string url = "https://www.bilibili.com/";//std::string url = "靜野孔文";//字符串經過處理后放入布隆過濾器for (size_t i = 0; i < N; ++i) v1.push_back(url + std::to_string(i));for (auto& str : v1) bf.Set(str);// v2跟v1是相似字符串集（前綴一樣），但是不一樣std::vector<std::string> v2;for (size_t i = 0; i < N; ++i) {string urlstr = url;urlstr += std::to_string(9999999 + i);v2.push_back(urlstr);}size_t n2 = 0;for (auto& str : v2)if (bf.Test(str))// 統計誤判的個數++n2;cout << "相似字符串誤判率:" << (double)n2 / (double)N << endl;// 不相似字符串集std::vector<std::string> v3;for (size_t i = 0; i < N; ++i) {string url = "九藍一金";url += std::to_string(i + rand());v3.push_back(url);}size_t n3 = 0;for (auto& str : v3) if (bf.Test(str)) ++n3; cout << "不相似字符串誤判率:" << (double)n3 / (double)N << endl;}
}

哈希切割

• 給一個超過100G大小的 log file , log 中存著 IP 地址, 設計算法找到出現次數最多的 IP 地址？與上題條件相同，如何找到 top K的 IP ？

log file 內部的數據不用想也是字符串。100G的大文件可以切分成若干個小文件，例如切分成100個；然后對大文件中每個IP地址通過函數$i=\text{Hash(query)}\%100$ 計算出這個IP應該存放在哪個小文件。

之所以這么做，是因為相同的IP一定會進入同一個文件。

這樣切分后，對每個小文件通過STL的工具map或unordered_map統計次數即可。小文件太大時再進行二次切分、三次切分即可。

統計 top K 可以先將map中的數據導出文件，然后再在內存中建堆，再將從map中讀出的數據重新讀回替換即可（詳見堆的應用——topk問題-CSDN博客）。

這種利用哈希算法的特性對文件進行切割的方法稱哈希切割。具體代碼實現以后有機會再做總結。

哈希切割的其他應用：

• 給兩個文件，分別有100億個query（查詢請求，本質還是字符串），我們只有1G內存，如何找到兩個文件交集？分別給出精確算法和近似算法。

近似算法就是布隆過濾器。但布隆過濾器的誤判，會導致一些非交集的query也被算進去。

粗略計算：假設平均一個query有 50 byte, 100億就是5000億，約等于500G，所以內存肯定是存不下的（不排除有超級計算機能存）。所以直接排除哈希表、紅黑樹等一眾依賴內存的數據結構。

還可以把1個大文件分成若干個小文件，例如分成500個小文件。然后讀取每個query，對每個query通過函數$i=\text{Hash(query)}\%500$確定這個query存放在哪個文件中，$\text{Hash(x)}$是某種字符串哈希。

將2個大文件分成2組小文件后，對2組小文件中編號相同的小文件找交集即可。

但還有一種極端情況：某個小文件的query太多，導致文件太大，無法裝進內存。這種小文件有2種情況：

1. 這個小文件中大多都是某1個query。
2. 這個小文件，有很多不同的query。

這時不管文件大小，直接讀到內存的set中。若是情況1，則重復的query都插入失敗，有可能全部插入set。若是情況2，則插入set中時會觸發異常，這時需要更換另一個哈希函數堆小文件進行二次切分甚至三次切分，然后逐一和另一個文件找交集。

具體代碼實現以后有機會再做總結。