Deep Learning_ Foundations and Concepts-Springer (2024)【拜讀】20章3節

在這里插入圖片描述

Diffusion Models 擴散模型

我們已經了解到，構建強大的生成模型的一種有效方法是：先引入一個關于潛在變量z的分布p(z)，然后使用深度神經網絡將z變換到數據空間x。由于神經網絡具有通用性，能夠將簡單固定的分布轉化為關于x的高度靈活的分布族，因此為p(z)采用如高斯分布N(z|0, I)這類簡單固定的分布就足夠了。在之前的章節中，我們探討了多種符合這一框架的模型，這些模型基于生成對抗網絡、變分自編碼器以及歸一化流，在定義和訓練深度神經網絡方面采用了不同的方法。

在本章中，我們將探討這一通用框架下的第四類模型，即擴散模型（diffusion models），也被稱為去噪擴散概率模型（denoising diffusion probabilistic models，簡稱DDPMs）（Sohl-Dickstein等人，2015年；Ho、Jain和Abbeel，2020年）。這類模型已成為許多應用領域中最先進的模型。為便于說明，我們將重點討論圖像數據模型，盡管該框架具有更廣泛的適用性。其核心思想是，對每張訓練圖像應用多步加噪過程，將其逐步破壞并最終轉化為一個服從高斯分布的樣本。這一過程如圖20.1所示。隨后，訓練一個深度神經網絡來逆轉這一過程；一旦訓練完成，該網絡就可以從高斯分布中采樣作為輸入，進而生成新的圖像。

擴散模型可被視為一種分層變分自編碼器的變體，其中編碼器分布是固定的，由加噪過程所定義，而僅需學習生成分布（Luo，2022）。這類模型易于訓練，在并行硬件上擴展性良好，且能規避對抗訓練中的挑戰與不穩定性問題，同時生成結果的質量可與生成對抗網絡相媲美甚至更優。然而，由于需要通過解碼器網絡進行多次前向傳播，生成新樣本的計算成本可能較高（Dhariwal和Nichol，2021）。

20.3 Score Matching

本章迄今討論的去噪擴散模型與另一類深度生成模型存在緊密關聯——這類模型基于得分匹配（Score Matching）理論（Hyv?rinen，2005；Song和Ermon，2019）獨立發展而來。它們的核心工具是得分函數（Score Function）或Stein得分，其定義為數據向量 $x$ 的對數似然函數關于 $x$ 的梯度，具體表達式為：
在這里插入圖片描述
在此需特別強調：該梯度是針對數據向量 $x$ 計算的，而非針對任何參數向量。需注意，得分函數 $s (x)$ 是一個與 $x$ 維度相同的向量值函數，其每個分量 $si(x)=?ln?p(x)?xis_i(x) = \frac{\partial \ln p(x)}{\partial x_i}$ 對應于 $x$ 的第 $i$ 個分量 $x_i$ 。例如，若 $x$ 為圖像，則 $s (x)$ 也可表示為同尺寸的圖像，其中每個像素對應原圖像的梯度值。圖20.5展示了一個二維概率密度函數及其對應的得分函數示例。

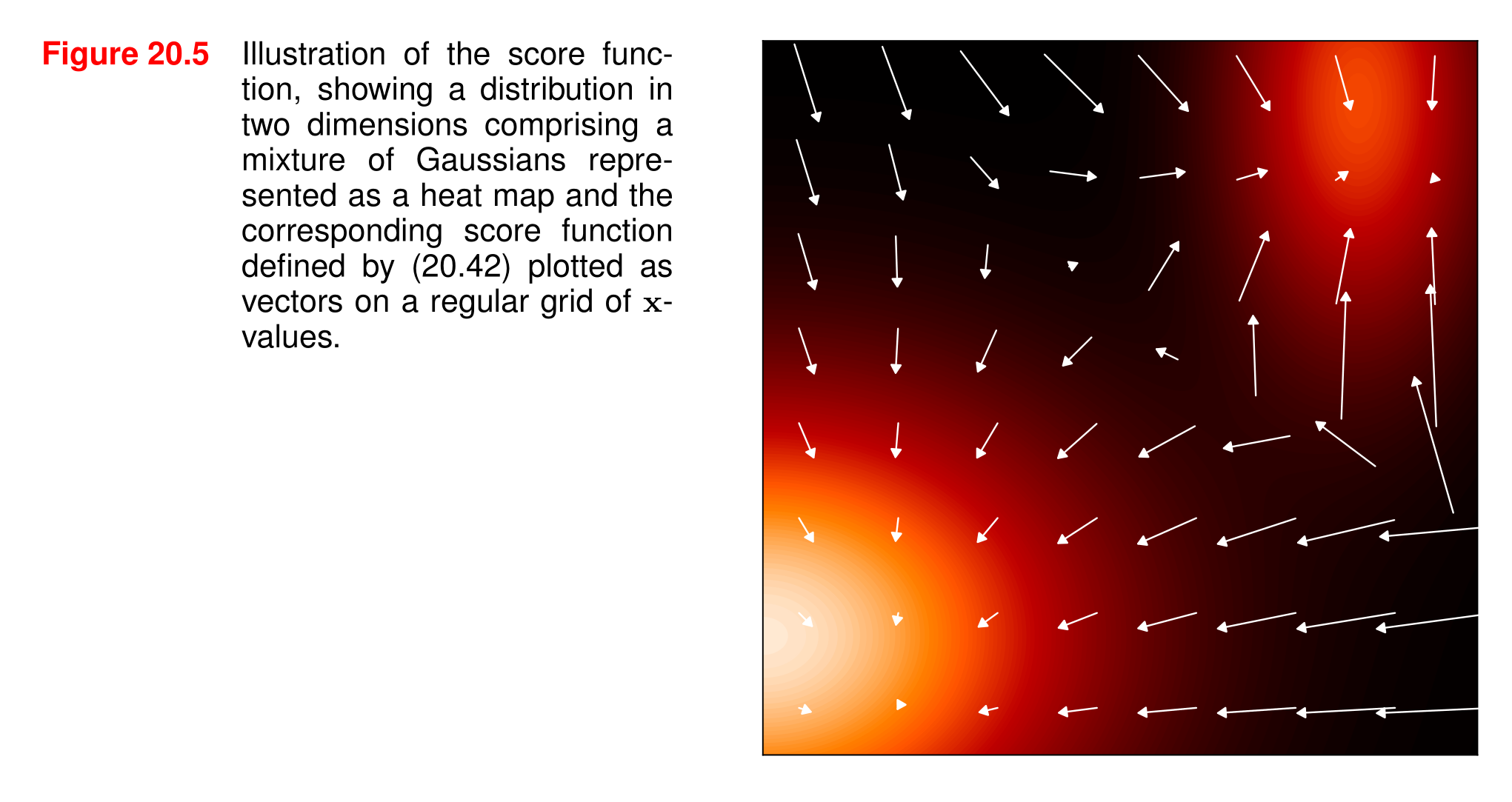
在這里插入圖片描述

圖20.5 分數函數的圖示，展示了二維空間中的一種分布，該分布由作為熱圖表示的高斯混合組成，以及由(20.42)定義的相應分數函數，以向量的形式繪制在規則的x值網格上。# 圖表解釋
這張圖展示了一個二維空間中的分布情況。圖中主要包含兩個部分的信息：
- **熱圖部分**：背景顏色表示了一個由多個高斯分布混合而成的概率分布。顏色越亮（如黃色、橙色區域），表示該區域的概率密度越高；顏色越暗（如黑色區域），表示概率密度越低。這種熱圖的可視化方式有助于直觀地理解分布的形狀和集中區域。
- **向量部分**：在規則的x值網格上繪制了向量，這些向量代表了由公式(20.42)定義的分數函數。向量的方向和長度傳達了分數函數在不同位置的信息，可能用于指示某種梯度、方向場或其他與分布相關的特性。總體而言，這張圖通過熱圖和向量的結合，提供了對二維空間中高斯混合分布及其相關分數函數的直觀可視化，有助于理解分布的結構和分數函數的行為。

要理解得分函數為何有用，可考慮兩個概率密度函數 $q (x)$ 和 $p (x)$ ，若它們的得分函數相等（即對所有 $x$ 滿足 $?xln?q(x)=?xln?p(x)\nabla_x \ln q(x) = \nabla_x \ln p(x)$ ），則對等式兩邊關于 $x$ 積分并取指數后，可得 $q (x) = K p (x)$ ，其中 $K$ 是與 $x$ 無關的常數。因此，若能通過模型 $s (x, w)$ 學習到得分函數，則相當于建模了原始數據密度 $p (x)$ （僅相差一個比例常數 $K$ ）。

20.3.1 Score loss function

要訓練這樣的模型，我們需要定義一個損失函數，其目標是使模型預測的得分函數 $s (x, w)$ 與生成數據的真實分布 $p (x)$ 的得分函數 $?xln?p(x)\nabla_x \ln p(x)$ 相匹配。此類損失函數的一個典型例子是模型得分與真實得分之間的期望平方誤差，其表達式為：

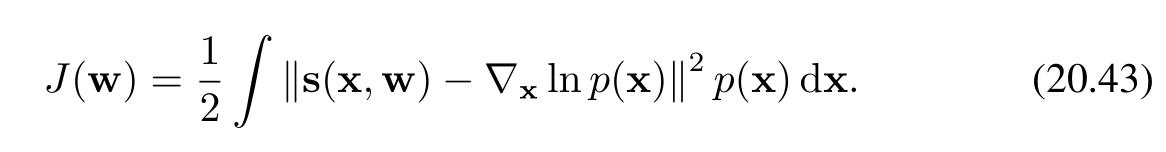
在這里插入圖片描述
正如我們在能量模型討論中提到的，得分函數無需假設相關概率密度已歸一化，因為梯度算子會消去歸一化常數，這為模型選擇提供了極大的靈活性。使用深度神經網絡表示得分函數 $s (x, w)$ 時，主要有兩種方法：

直接輸出法：由于得分函數的每個分量 $s_i$ 對應數據 $x$ 的第 $i$ 個分量 $x_i$ ，因此可設計一個神經網絡，使其輸出維度與輸入維度相同。
梯度計算法：得分函數本質上是標量函數（對數概率密度）的梯度，屬于更受限的函數類。因此另一種方法是構建一個僅輸出標量 $?(x)\phi(x)$ 的網絡，再通過自動微分計算 $?x?(x)\nabla_x \phi(x)$ 。不過，這種方法需要兩次反向傳播（一次計算 $?(x)\phi(x)$ ，一次計算梯度），計算成本更高。

由于上述原因，大多數實際應用采用第一種方法。

20.3.2 Modified score loss

損失函數（20.43）存在的一個關鍵問題是：我們無法直接對其進行最小化優化，因為真實數據的得分函數 $?xln?p(x)\nabla_x \ln p(x)$ 是未知的。我們手中僅有的資源是有限的數據集 $D={x1,…,xN}\mathcal{D} = \{x_1, \ldots, x_N\}$ ，通過它可以構造一個經驗分布（empirical distribution）：

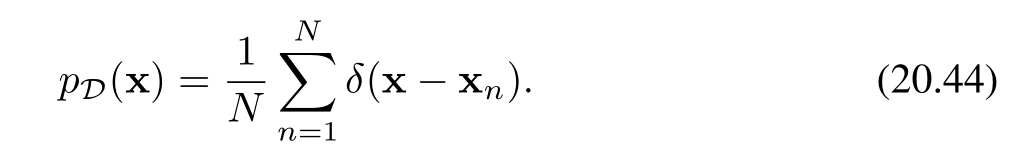
在這里插入圖片描述
其中 $δ(x)\delta(x)$ 是狄拉克δ函數（Dirac delta function），可直觀理解為在 $x = 0$ 處的一個無限高、無限窄的“尖峰”，其具有以下特性：

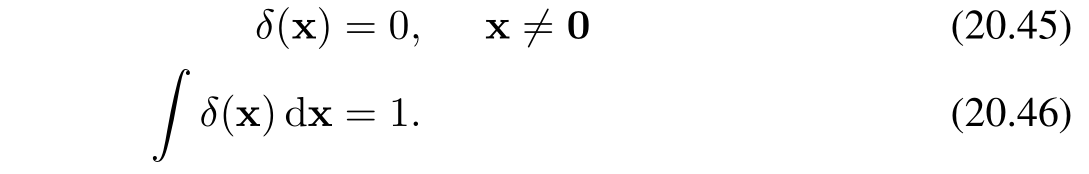
由于式（20.44）關于 $x$ 不可微，因此無法直接計算其得分函數。為解決這一問題，可通過引入噪聲模型對數據點進行**“平滑處理”，從而得到一個光滑且可微的概率密度表示。這種方法被稱為帕森窗估計（Parzen Estimator）或核密度估計（Kernel Density Estimator），其定義為：

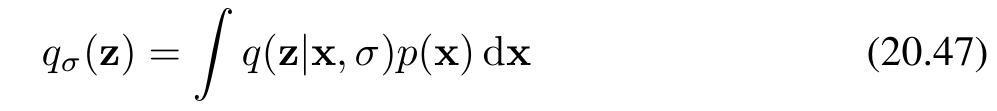
其中 $\sigma)$ 是噪聲核函數。一種常用的核函數選擇是高斯核（Gaussian Kernel）**，即：
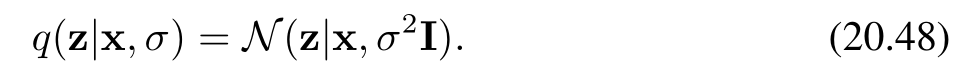
在這里插入圖片描述

通過引入噪聲模型和高斯核函數，我們可以將離散的經驗分布轉換為連續且可微的密度估計，從而能夠計算分數函數并進行后續的優化和建模工作。這種方法在處理有限數據集和構建可微的概率密度模型時非常有用。

此時我們不再直接最小化損失函數（20.43），而是改用針對平滑后的帕森密度（Parzen density）的對應損失函數，其形式為：
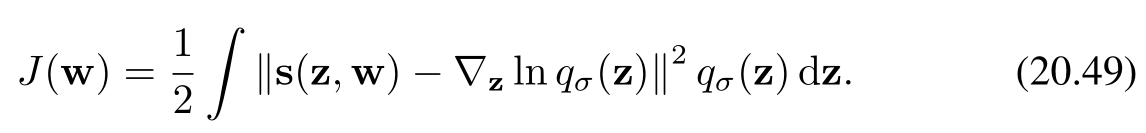
在這里插入圖片描述

一個關鍵的結果是，把公式(20.47)代入到公式(20.49)中，能夠將損失函數重新寫成由(Vincent, 2011)給出的等效形式。這里的核心在于通過特定的代入操作，對損失函數進行形式上的轉換，以便更好地進行分析和處理。

等效形式的損失函數
改寫后的損失函數 $J(w)J(\mathbf{w})$ 的表達式為：
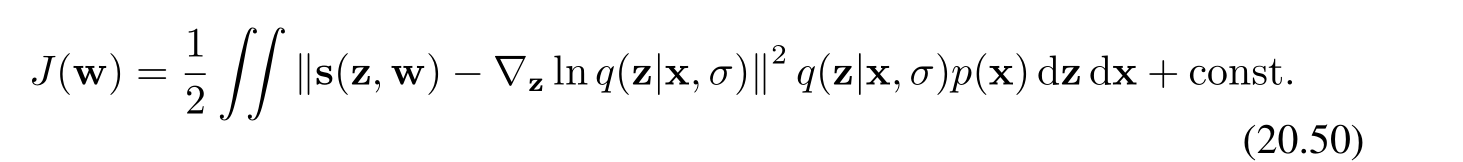
在這里插入圖片描述

這個表達式是損失函數在一般情況下的等效形式。其中：

$s(z,w)\mathbf{s}(\mathbf{z}, \mathbf{w})$ 是我們學習的分數函數模型， $w\mathbf{w}$ 是模型的參數。
$?zln?q(z∣x,σ)\nabla_{\mathbf{z}} \ln q(\mathbf{z}|\mathbf{x}, \sigma)$ 是條件概率分布 $q(z∣x,σ)q(\mathbf{z}|\mathbf{x}, \sigma)$ 的對數關于 $z\mathbf{z}$ 的梯度，也就是分數函數。
$q(z∣x,σ)q(\mathbf{z}|\mathbf{x}, \sigma)$ 是噪聲核函數，通常為高斯核函數 $N(z∣x,σ2I)\mathcal{N}(\mathbf{z}|\mathbf{x}, \sigma^2 \mathbf{I})$ 。
$p(x)p(\mathbf{x})$ 是原始數據的概率密度函數。
整個積分表達式衡量了學習到的分數函數模型與真實的分數函數之間的差異，通過積分在所有可能的 $x\mathbf{x}$ 和 $z\mathbf{z}$ 上進行加權平均。

使用經驗密度代入后的損失函數
如果我們使用經驗密度（20.44）來代替 $p(x)p(\mathbf{x})$ ，即用有限的數據集來近似原始數據的分布，那么損失函數 $J(w)J(\mathbf{w})$ 變為：
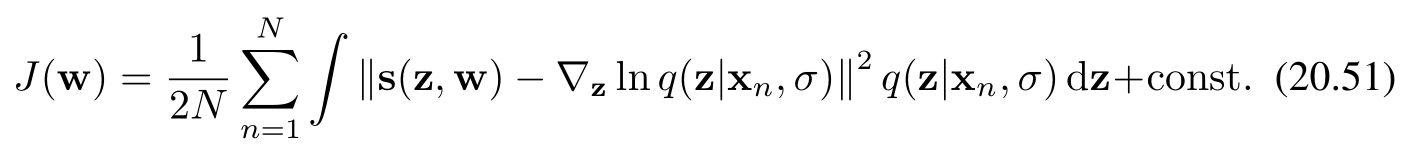
在這里插入圖片描述

這里，求和是對數據集中的 $N$ 個數據點 $xn\mathbf{x}_n$ 進行的。通過使用經驗密度，我們將連續的積分形式轉換為了離散的求和形式，這使得在實際應用中，當我們只有有限的數據樣本時，能夠更方便地計算和優化損失函數。

總體而言，這部分內容展示了如何通過特定的代入操作和經驗密度的使用，將損失函數轉換為更便于實際應用的形式，為后續的模型訓練和優化提供了基礎。

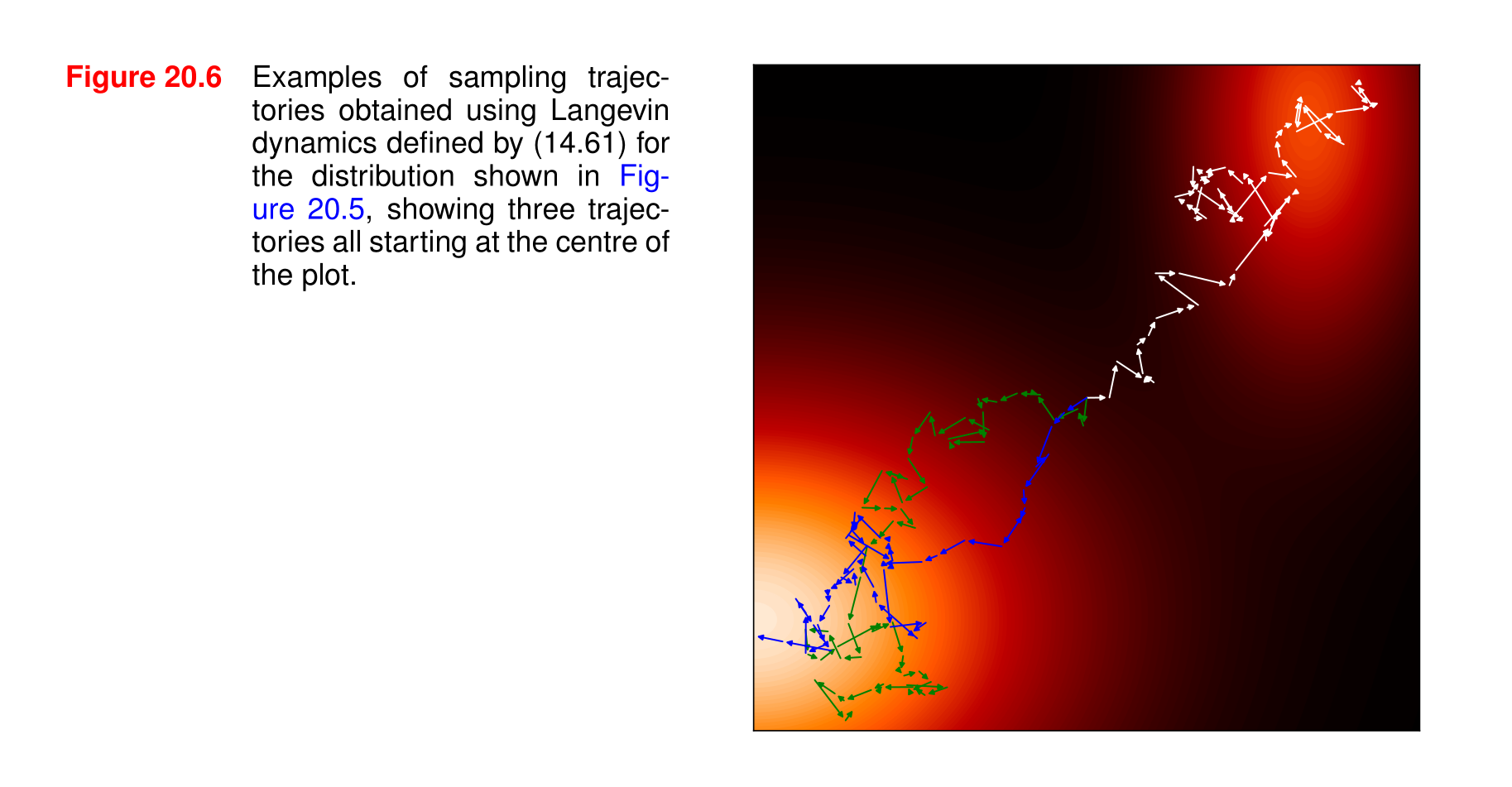
在這里插入圖片描述
圖20.6 使用由(14.61)定義的朗之萬動力學（Langevin dynamics）對圖20.5中所示的分布進行采樣得到的軌跡示例，展示了三條均從繪圖中心開始的軌跡。

### 詳細解析
1. **朗之萬動力學（Langevin dynamics）**- 朗之萬動力學是一種用于描述隨機過程的物理模型，常用于從復雜的概率分布中進行采樣。在機器學習和統計物理中，它被廣泛應用于模擬分子運動、優化算法以及概率密度估計等任務。公式(14.61)定義了具體的朗之萬動力學方程，雖然圖中未給出該公式的具體內容，但通常朗之萬方程會包含確定性力和隨機力兩部分，用于描述系統在隨機噪聲影響下的演化過程。
2. **對圖20.5中分布的采樣**- 圖20.5展示了一個二維空間中的分布，該分布由高斯混合表示，并通過熱圖和向量進行了可視化。這里的采樣是指根據圖20.5所表示的概率分布生成樣本點，而朗之萬動力學提供了一種從該分布中生成樣本的動態方法。通過模擬朗之萬動力學過程，可以生成一系列的樣本點，這些樣本點的軌跡反映了系統在概率空間中的演化路徑。
3. **軌跡示例**- 圖20.6展示了三條采樣軌跡，這些軌跡都從繪圖的中心開始。每條軌跡由一系列的點組成，點之間的連線表示系統在不同時間步的演化路徑。軌跡上的箭頭可能表示系統在每個時間步的移動方向，反映了朗之萬動力學中確定性力和隨機力的綜合作用。- 從圖中可以看出，不同的軌跡在演化過程中會受到隨機噪聲的影響，從而呈現出不同的路徑。盡管起始點相同，但由于隨機力的存在，軌跡會逐漸分散，覆蓋概率分布的不同區域。這展示了朗之萬動力學在探索復雜概率分布空間時的隨機性和多樣性。總體而言，圖20.6通過具體的軌跡示例，直觀地展示了如何使用朗之萬動力學從給定的概率分布中進行采樣，以及采樣過程中系統的動態演化特征。

對于高斯帕曾核（Gaussian Parzen kernel）（公式20.48），分數函數變為：
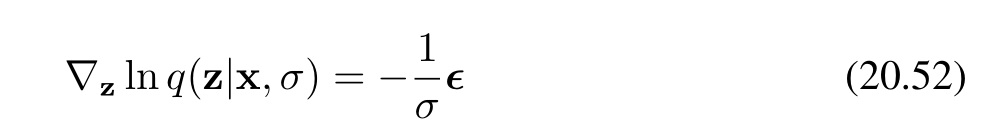
在這里插入圖片描述

其中 $?=z?x\boldsymbol{\epsilon} = \mathbf{z} - \mathbf{x}$ 是從 $N(z∣0,I)\mathcal{N}(\mathbf{z}|\mathbf{0}, \mathbf{I})$ 中抽取的。如果我們考慮特定的噪聲模型（公式20.6），則得到：
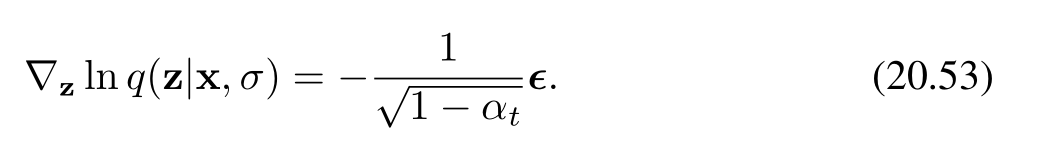
在這里插入圖片描述

因此，我們可以看到分數損失（公式20.50）衡量的是神經網絡預測與噪聲 $?\boldsymbol{\epsilon}$ 之間的差異。所以，這個損失函數與去噪擴散模型中使用的（公式20.37）形式具有相同的最小值，分數函數 $s(z,w)\mathbf{s}(\mathbf{z}, \mathbf{w})$ 起著與噪聲預測網絡 $g(z,w)\mathbf{g}(\mathbf{z}, \mathbf{w})$ 相同的作用，只是有一個常數縮放因子 $?1/1?αt-1/\sqrt{1 - \alpha_t}$ （Song和Ermon，2019）。最小化（公式20.50）被稱為去噪分數匹配，我們可以看到它與去噪擴散模型的緊密聯系。關于如何選擇噪聲方差 $σ2\sigma^2$ 的問題仍然存在，我們很快會回到這個問題。

在訓練了一個基于分數的模型后，我們需要抽取新的樣本。朗之萬動力學非常適合基于分數的模型，因為它基于分數函數，因此不需要歸一化的概率分布，如圖20.6所示。

解釋

分數函數的推導
- 首先，針對高斯帕曾核，通過對數條件概率關于 $z\mathbf{z}$ 求梯度，得到了分數函數的表達式（公式20.52），其中 $?\boldsymbol{\epsilon}$ 是從標準正態分布中抽取的。
- 當考慮特定的噪聲模型時，分數函數的表達式變為（公式20.53），這里引入了與噪聲模型相關的參數 $αt\alpha_t$ 。
分數損失與去噪擴散模型的聯系
- 分數損失（公式20.50）的作用是衡量神經網絡預測和噪聲之間的差異。
- 該損失函數與去噪擴散模型中的某個形式（公式20.37）具有相同的最小值，基于分數的模型中的分數函數 $s(z,w)\mathbf{s}(\mathbf{z}, \mathbf{w})$ 和去噪擴散模型中的噪聲預測網絡 $g(z,w)\mathbf{g}(\mathbf{z}, \mathbf{w})$ 功能相似，只是存在一個常數縮放因子。
- 最小化分數損失的過程被稱為去噪分數匹配，這顯示了基于分數的模型與去噪擴散模型之間的緊密聯系。
樣本抽取與朗之萬動力學
- 訓練好基于分數的模型后，需要抽取新樣本。
- 朗之萬動力學適用于基于分數的模型，因為它直接利用分數函數，不需要歸一化的概率分布，圖20.6展示了使用朗之萬動力學進行采樣的軌跡示例。
未解決的問題
- 文中指出，關于如何選擇噪聲方差 $σ2\sigma^2$ 的問題仍然存在，后續會進一步討論這個問題。

20.3.3 Noise variance 噪聲方差

我們已經了解了如何從一組訓練數據中學習分數函數，以及如何使用朗之萬采樣（Langevin sampling）從學習到的分布中生成新樣本。然而，我們可以發現這種方法存在三個潛在問題（Song和Ermon，2019；Luo，2022）。

首先，如果數據分布位于一個維度低于數據空間的流形（manifold）上，那么在流形之外的點處，概率密度為零，并且由于 $ln?p(x)\ln p(x)$ 無定義，此處分數函數也無定義。

其次，在數據密度較低的區域，由于損失函數（20.43）是按密度加權的，因此對分數函數的估計可能不準確。使用朗之萬采樣時，不準確的分數函數可能會導致生成較差的軌跡。

第三，即使分數函數的模型準確，如果數據分布由多個不相交的分布混合而成，朗之萬過程也可能無法正確采樣。

這三個問題都可以通過為核函數（20.48）中使用的噪聲方差 $σ2\sigma^2$ 選擇一個足夠大的值來解決，因為這樣會使數據分布變得模糊（平滑）。然而，方差過大會嚴重扭曲原始分布，這本身就會導致分數函數建模的不準確。可以通過考慮一系列方差值 $σ12<σ22<?<σT2\sigma^2_1 < \sigma^2_2 < \cdots < \sigma^2_T$ （Song和Ermon，2019）來處理這種權衡，其中 $σ12\sigma^2_1$ 足夠小，能夠準確表示數據分布，而 $σT2\sigma^2_T$ 足夠大，可以避免上述問題。

然后，分數網絡被修改為將方差作為額外輸入 $s(x,w,σ2)s(\mathbf{x}, \mathbf{w}, \sigma^2)$ ，并通過使用一個加權和形式的損失函數進行訓練，該損失函數是形式為（20.51）的損失函數的加權總和，其中每一項表示相關網絡與相應擾動數據集之間的誤差。對于數據向量 $xn\mathbf{x}_n$ ，損失函數的形式則為

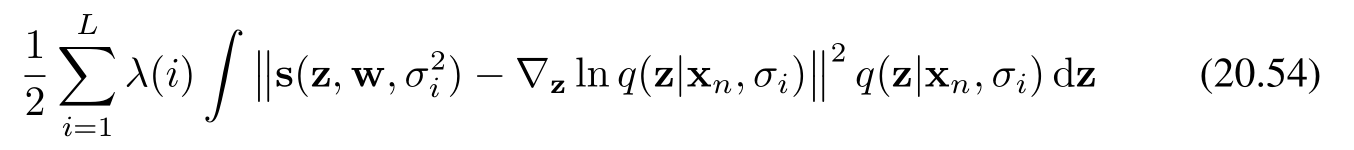
在這里插入圖片描述
其中 $λ(i)\lambda^{(i)}$ 是權重系數。我們可以看到，這種訓練過程與用于訓練分層去噪網絡的訓練過程完全對應（意思一致、相呼應）。

訓練完成后，可按順序依次針對 $\ldots, 2, 1$ 的各個模型，運行若干步朗之萬采樣來生成樣本。這種技術被稱為退火朗之萬動力學（annealed Langevin dynamics），其原理與用于從去噪擴散模型中采樣的算法20.2類似。

20.3.4 Stochastic differential equations 隨機微分方程

我們已看到，在為擴散模型構建噪聲過程時，采用大量步驟（通常多達數千步）是很有幫助的。因此，很自然地我們會思考：若像引入神經微分方程時對無限深層神經網絡所做的那樣，考慮無限步數的極限情況，會發生什么？在求取這種極限時，我們需要確保每一步的噪聲方差（見18.3.1節） $βt\beta_t$ 隨步長的減小而變小。這促使我們將擴散模型在連續時間下的形式表述為隨機微分方程（Stochastic Differential Equations，SDEs）（Song等人，2020）。如此一來，去噪擴散概率模型和分數匹配模型都可被視為連續時間隨機微分方程的一種離散化形式。

我們可以將一般的隨機微分方程（SDE）寫成對向量 $z\mathbf{z}$ 的無窮小更新的形式，即
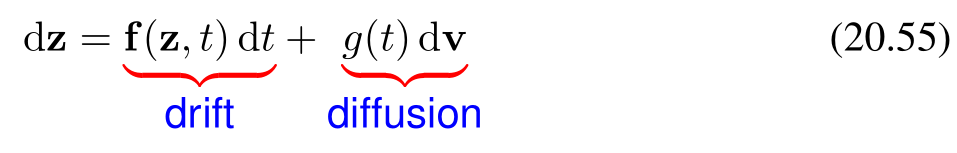
在這里插入圖片描述
其中，漂移項（drift term）如同常微分方程（ODE）中那樣是確定性的，但擴散項（diffusion term）是隨機的，例如由無窮小的高斯步長給出。這里的參數 $t$ 借物理系統的類比，常被稱為“時間”。通過對連續時間極限的推導，擴散模型的正向噪聲過程（20.3）可表示為（20.55）形式的隨機微分方程。

對于隨機微分方程（SDE）(20.55)，存在相應的逆向隨機微分方程（Song等人，2020），由下式給出：

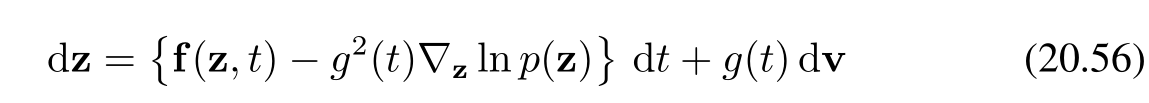
在這里插入圖片描述

其中，我們認定 $?zln?p(z)\nabla_{\mathbf{z}} \ln p(\mathbf{z})$ 為分數函數。需從 $t = T$ 到 $t = 0$ 逆向求解由(20.55)給出的隨機微分方程。

為了數值求解隨機微分方程，我們需要對時間變量進行離散化。最簡單的方法是使用固定且等間距的時間步長，這被稱為歐拉 - 瑪雅那（Euler - Maruyama）求解器。對于逆向隨機微分方程，我們則恢復一種朗之萬方程的形式。然而，可以采用更復雜的求解器，它們使用更靈活的離散化形式（Kloeden和Platen，2013）。

對于所有由隨機微分方程控制的擴散過程，存在一個由常微分方程（ODE）描述的相應確定性過程，其軌跡具有與隨機微分方程相同的邊際概率密度 $p(z∣t)p(\mathbf{z}|t)$ （Song等人，2020）。對于形式為(20.56)的隨機微分方程，相應的常微分方程由下式給出：

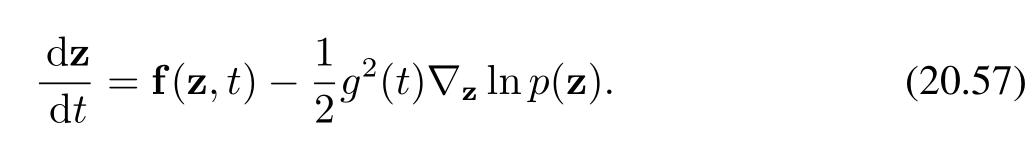
在這里插入圖片描述

常微分方程的公式化表述允許使用高效的自適應步長求解器，從而大幅減少函數求值的次數。此外，它使得概率擴散模型與歸一化流模型相關聯，從中可以使用變量變換公式(18.1)來提供對數似然的精確估計。

解釋

這段內容主要圍繞隨機微分方程（SDE）及其相關概念展開：

逆向隨機微分方程：介紹了與給定隨機微分方程(20.55)對應的逆向隨機微分方程(20.56)，并指出其中 $?zln?p(z)\nabla_{\mathbf{z}} \ln p(\mathbf{z})$ 為分數函數，且說明了求解該逆向隨機微分方程的時間范圍。
隨機微分方程的數值求解：闡述了數值求解隨機微分方程需要對時間變量離散化，介紹了最簡單的歐拉 - 瑪雅那求解器，以及對于逆向隨機微分方程可恢復朗之萬方程形式，還提到有更復雜的求解器可采用。
確定性過程與常微分方程：說明對于由隨機微分方程控制的擴散過程，存在具有相同邊際概率密度的確定性過程，由常微分方程描述，并給出了形式為(20.56)的隨機微分方程對應的常微分方程(20.57)。
常微分方程的優勢：指出常微分方程的公式化表述可使用高效自適應步長求解器，減少函數求值次數，還能使概率擴散模型與歸一化流模型相關聯，用于精確估計對數似然。