目? 錄

一、實驗學時

二、實驗目的

三、實驗要求

四、實驗內容

五、實驗步驟

1、打開Logisim軟件，列出并行四位二進制全加器邏輯電路真值表，并使用與、或、非、異或等基本原件實現并行四位二進制全加器邏輯電路，鋪設完成后進行測試進而判斷電路是否鋪設成功。

2、打開Logisim軟件，在第一步實現的并行四位二進制全加器的基礎上構建包括溢出、符號、歸零、進位等檢測功能的四位二進制運算器，鋪設完成后進行測試進而判斷電路是否鋪設成功。

3、打開Logisim軟件，利用兩個四位二進制加法器實現八位串行加法器，列出八位串行加法器邏輯電路真值表，并使用兩個四位二進制加法器實現八位串行加法器邏輯電路，鋪設完成后進行測試進而判斷電路是否鋪設成功。

4、打開Logisim軟件，利用兩個四位二進制加法器實現八位并行加法器，列出八位并行加法器邏輯電路真值表，并使用兩個四位二進制加法器實現八位并行加法器邏輯電路，鋪設完成后進行測試進而判斷電路是否鋪設成功。

5、打開Logisim軟件，用自己學號（20212501238）最后兩位數字（38）轉化為二進制（00000011，00001000）作為輸入，測試兩個八位加法器的功能。

六、實驗小結

1、問題和解決方法：

2、心得體會：

---

一、實驗學時

????????課堂2學時，課后2學時

二、實驗目的

????????1） 熟悉Logisim軟件的使用方法。

????????2） 掌握四位全加器邏輯電路實現方法。

????????3） 掌握八位全加器設計。

三、實驗要求

????????1）做好實驗預習，復習基本數字邏輯電路的原理，掌握實驗元器件的功能特性。

????????2）按照實驗內容與步驟的要求，獨立思考，認真仔細地完成實驗。

????????3）書寫實驗報告。

四、實驗內容

????????四位并行加法器電路圖如下：

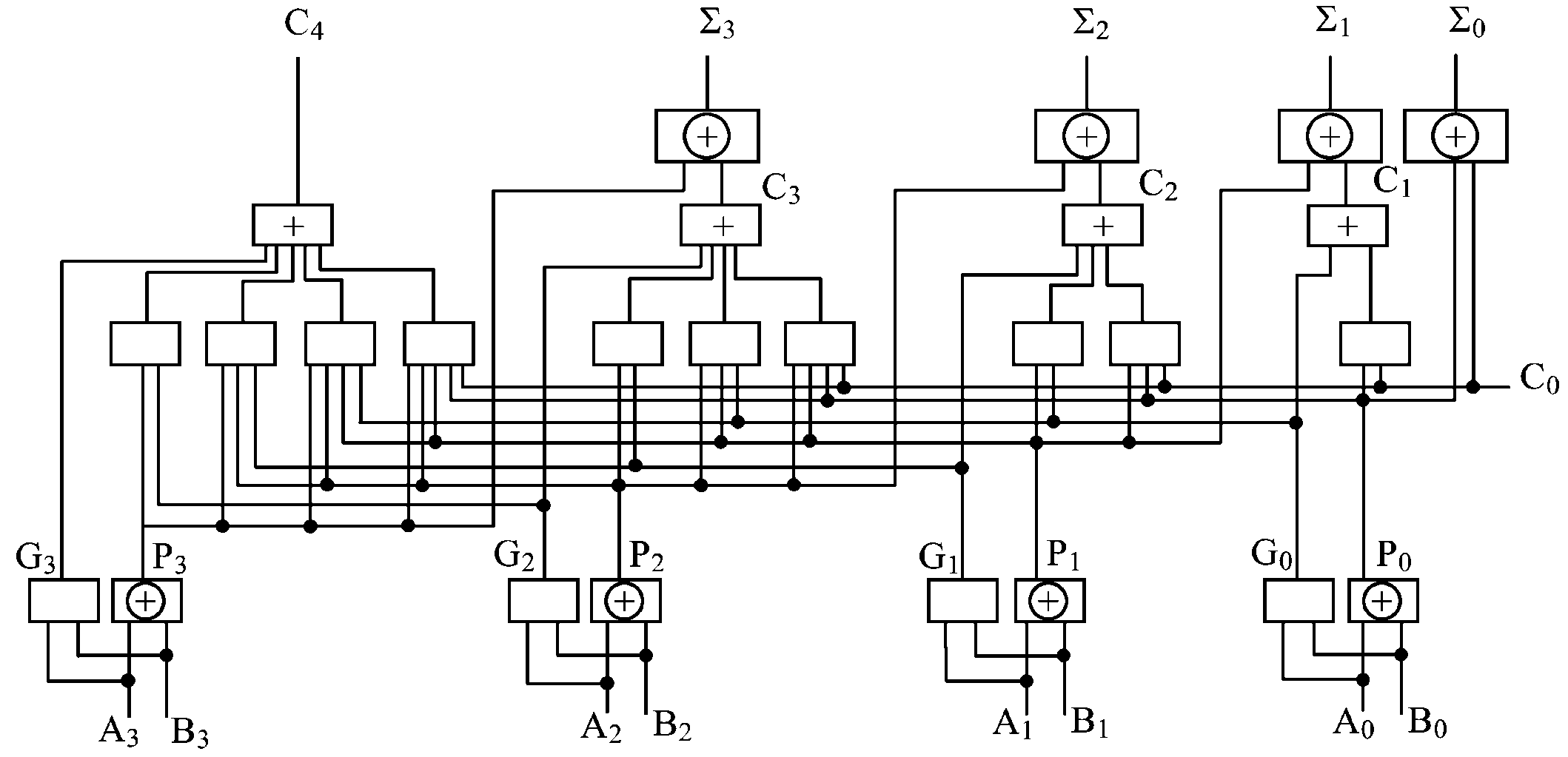
圖4-1 四位并行全加器電路圖

????????1、請按照給定的電路圖在logisim下實現4位2進制全加器仿真電路，并進行功能驗證。

????????2、請在完成第一步的基礎上，構建包括溢出、符號、歸零、進位等檢測功能的四位二進制運算器，具體功能如下示意圖所示，請完成Logisim仿真電路搭建及功能驗證。

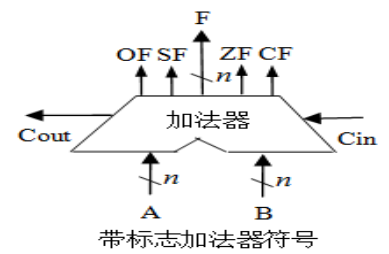
圖4-2 ?所需電路及工作區

????????3、利用兩個四位二進制運算器，分別實現八位串行加法器、八位并行加法器。

????????4、用自己學號最后兩位數字轉化為二進制作為輸入，測試兩個八位加法器功能。記錄各輸出端結果。

五、實驗步驟

1、打開Logisim軟件，列出并行四位二進制全加器邏輯電路真值表，并使用與、或、非、異或等基本原件實現并行四位二進制全加器邏輯電路，鋪設完成后進行測試進而判斷電路是否鋪設成功。

????????（1）使用邏輯公式G=AB，P=A?B，CI=G+PC（G為A與【AND】B后的結果值，P為A異或B的結果值，CI為先P與【AND】C再和G進行或操作【OR】后得到的結果值，⊕為異或符號，C為低位的進位，CI為高位的進位）完成對并行四位二進制全加器邏輯電路的實現，對應的部分并行四位二進制全加器邏輯電路真值表如圖5-1-1所示：

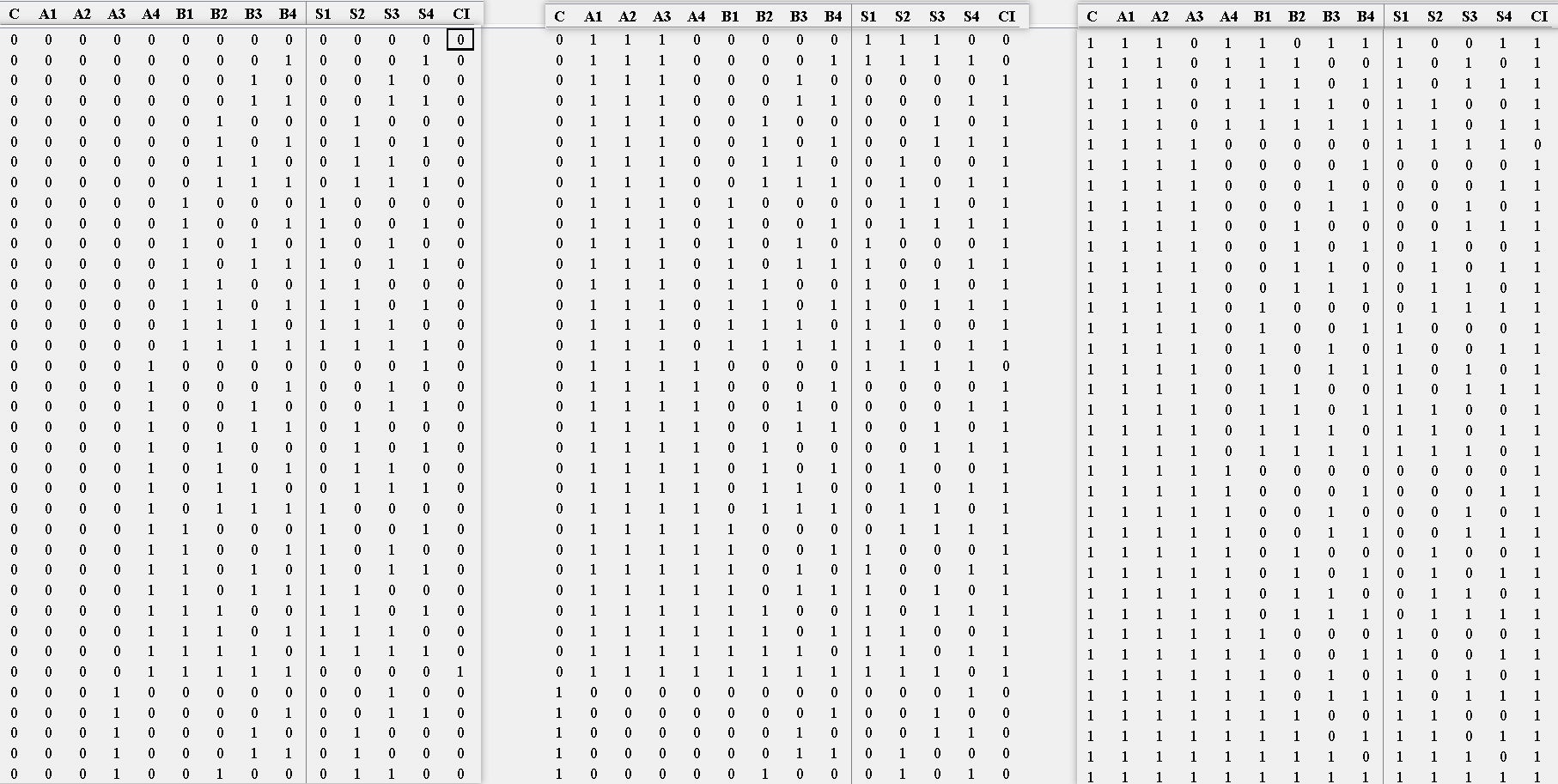
圖5-1-1 并行四位二進制全加器邏輯電路真值表

????????（2）依據邏輯公式完成并行四位二進制全加器邏輯電路的架構，輸入端A1、B1、C，先讓A1和B1進行與操作后得到G1；再讓A1和B1進行異或操作后得到P1；然后讓P1和C進行與操作后再和G1進行或操作得到CI；最后將P1和C進行異或操作后得到S1，在運行過程中低位的高位進位是高位的低位進位，依次類推到A4和B4，對應的并行四位二進制全加器邏輯電路如圖5-1-2所示：

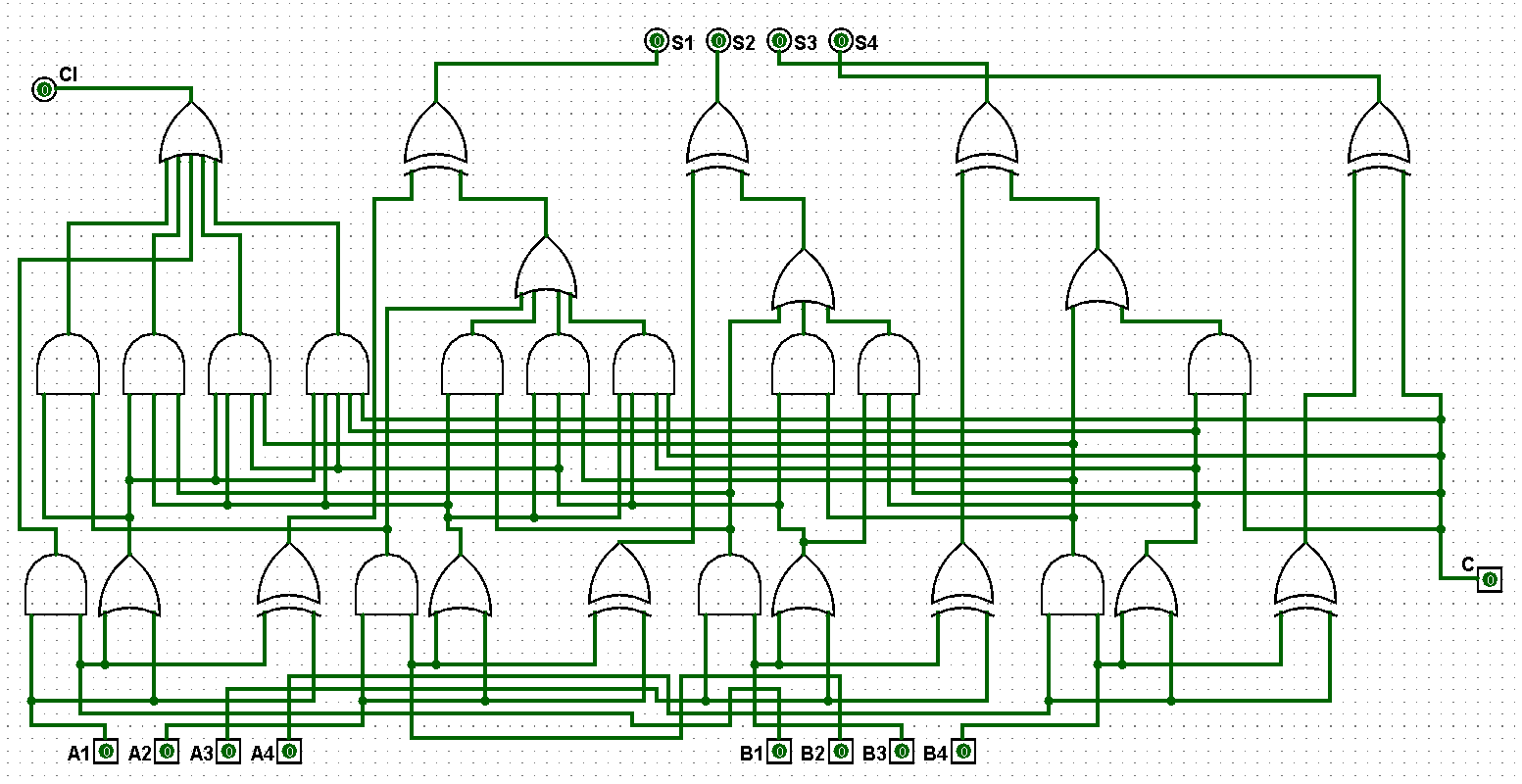
圖5-1-2 并行四位二進制全加器邏輯電路

????????（3）并行四位二進制全加器邏輯電路鋪設完畢后進行測試，進而判斷自己的電路是否鋪設成功，經過測試后此電路狀態一切正常，對應的并行四位二進制全加器邏輯電路測試如圖5-1-3至5-1-10所示：

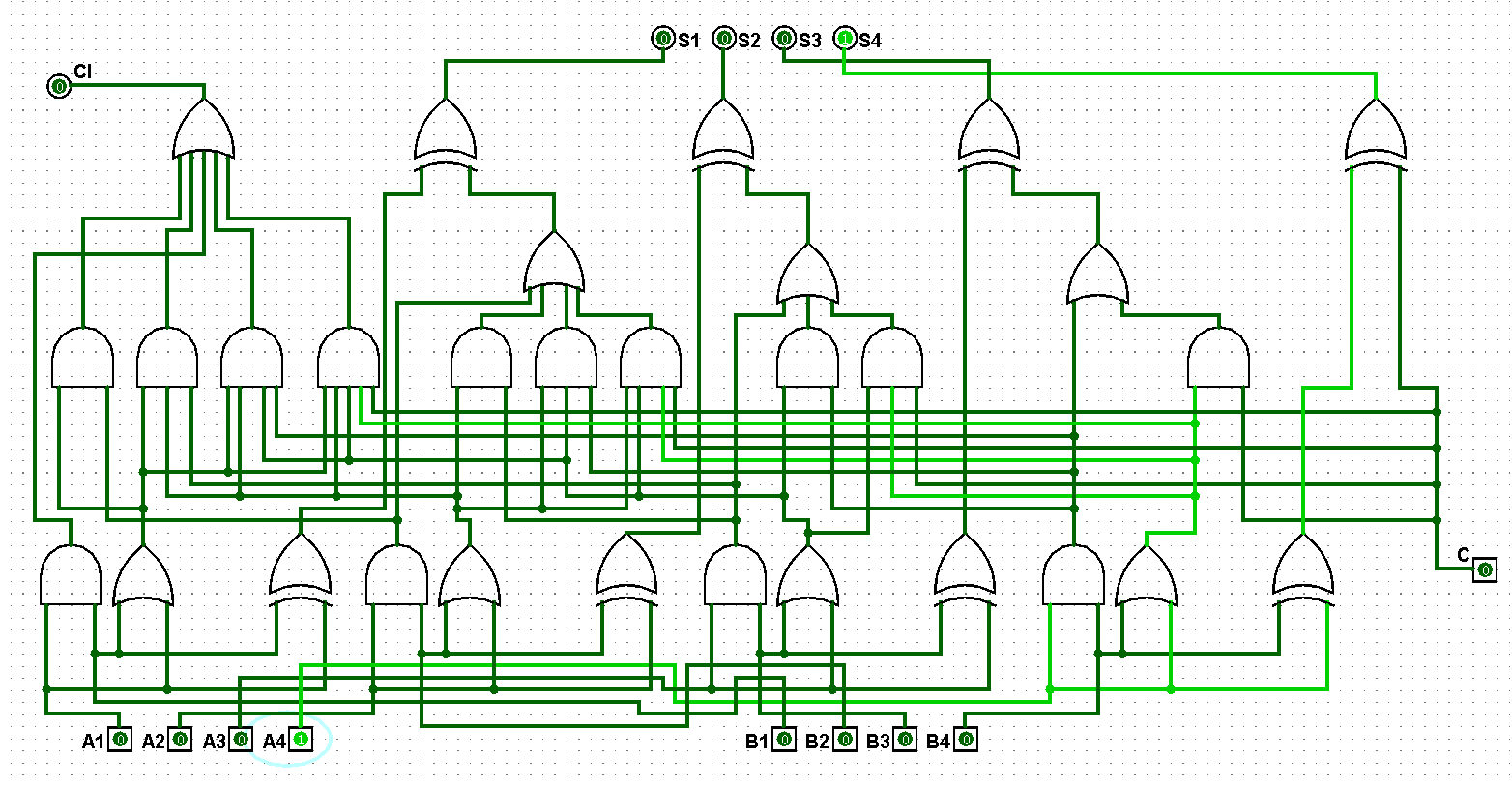
圖5-1-3 并行四位二進制全加器測試1+0=1

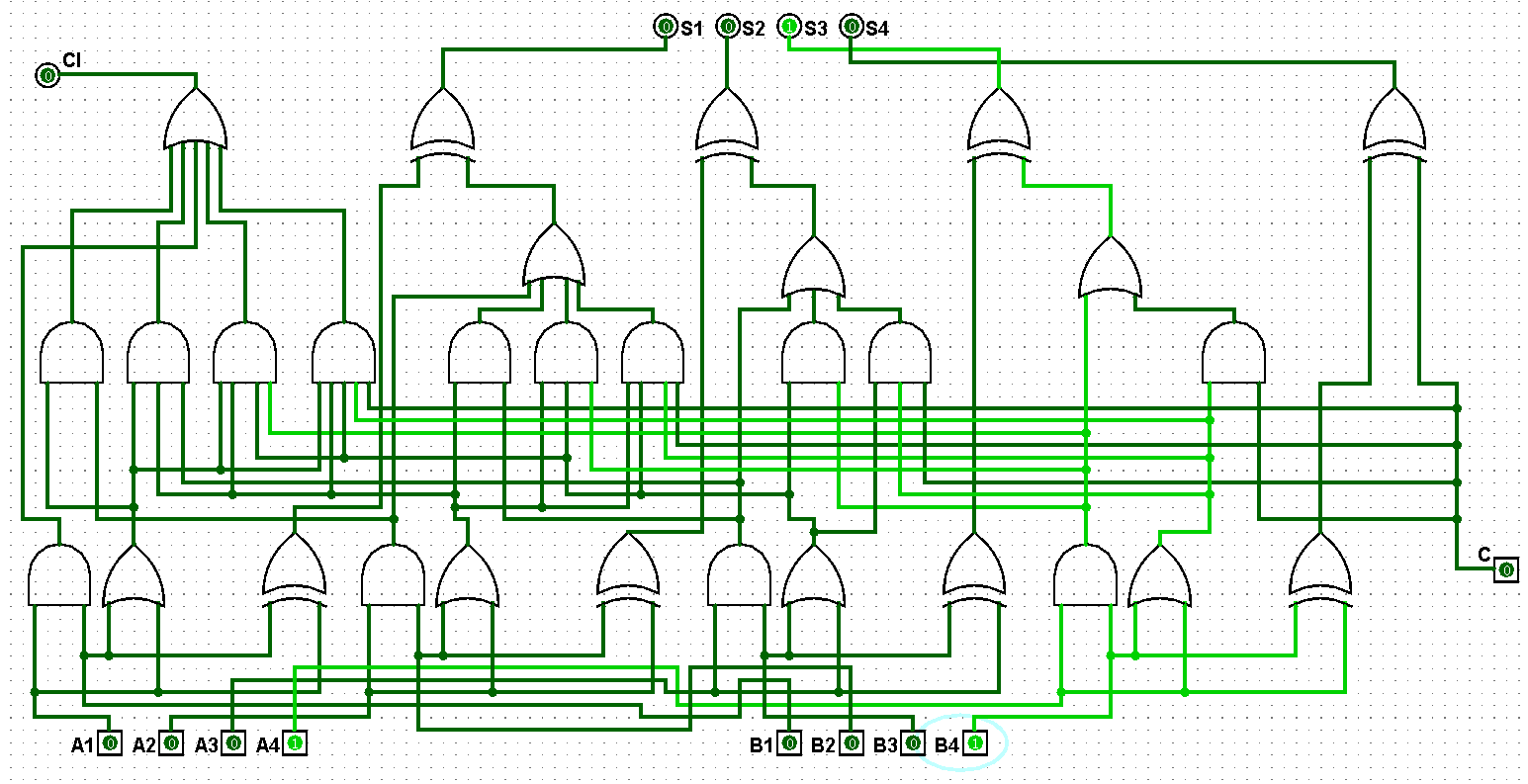
圖5-1-4 并行四位二進制全加器測試1+1=2

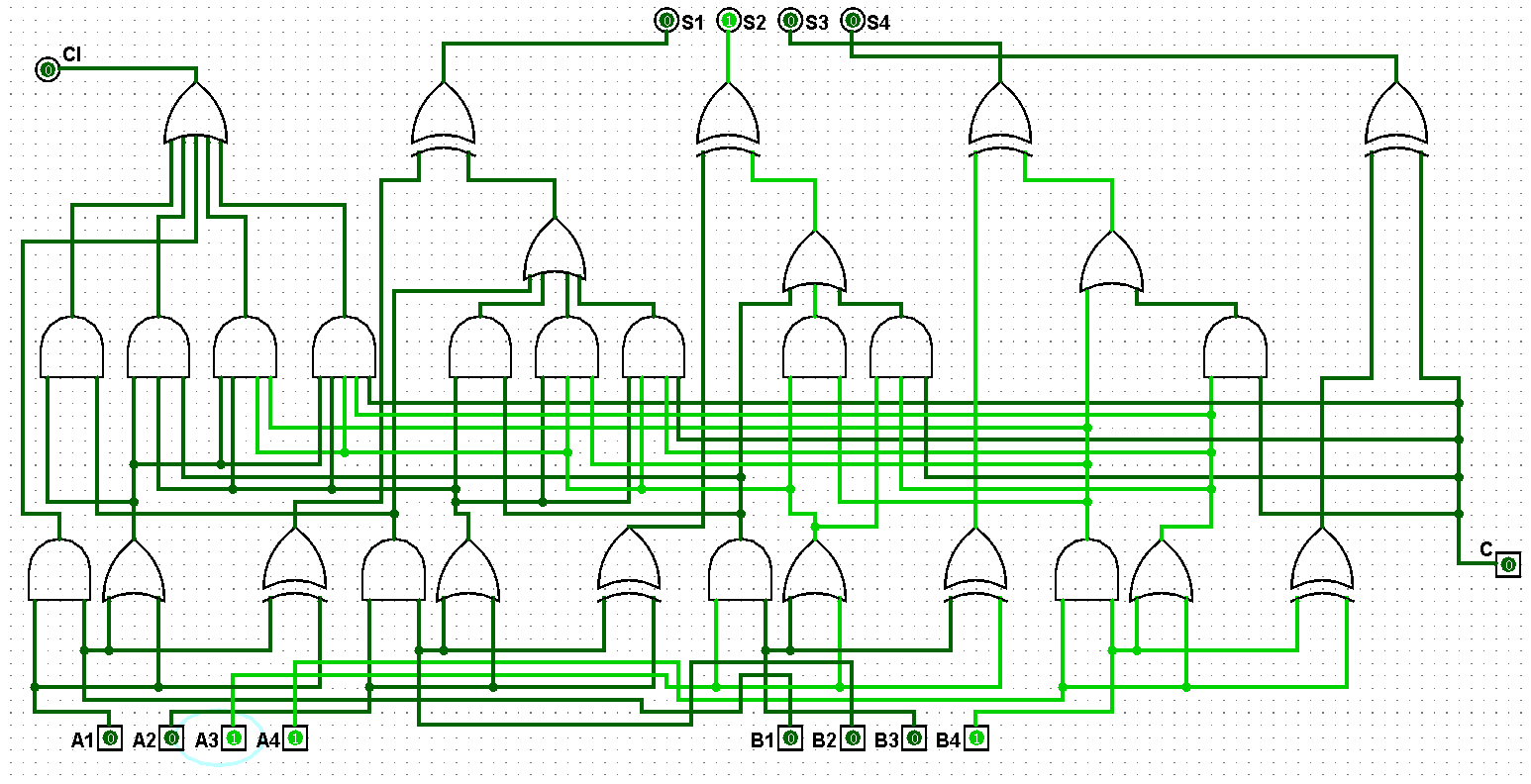
圖5-1-5 并行四位二進制全加器測試3+1=4

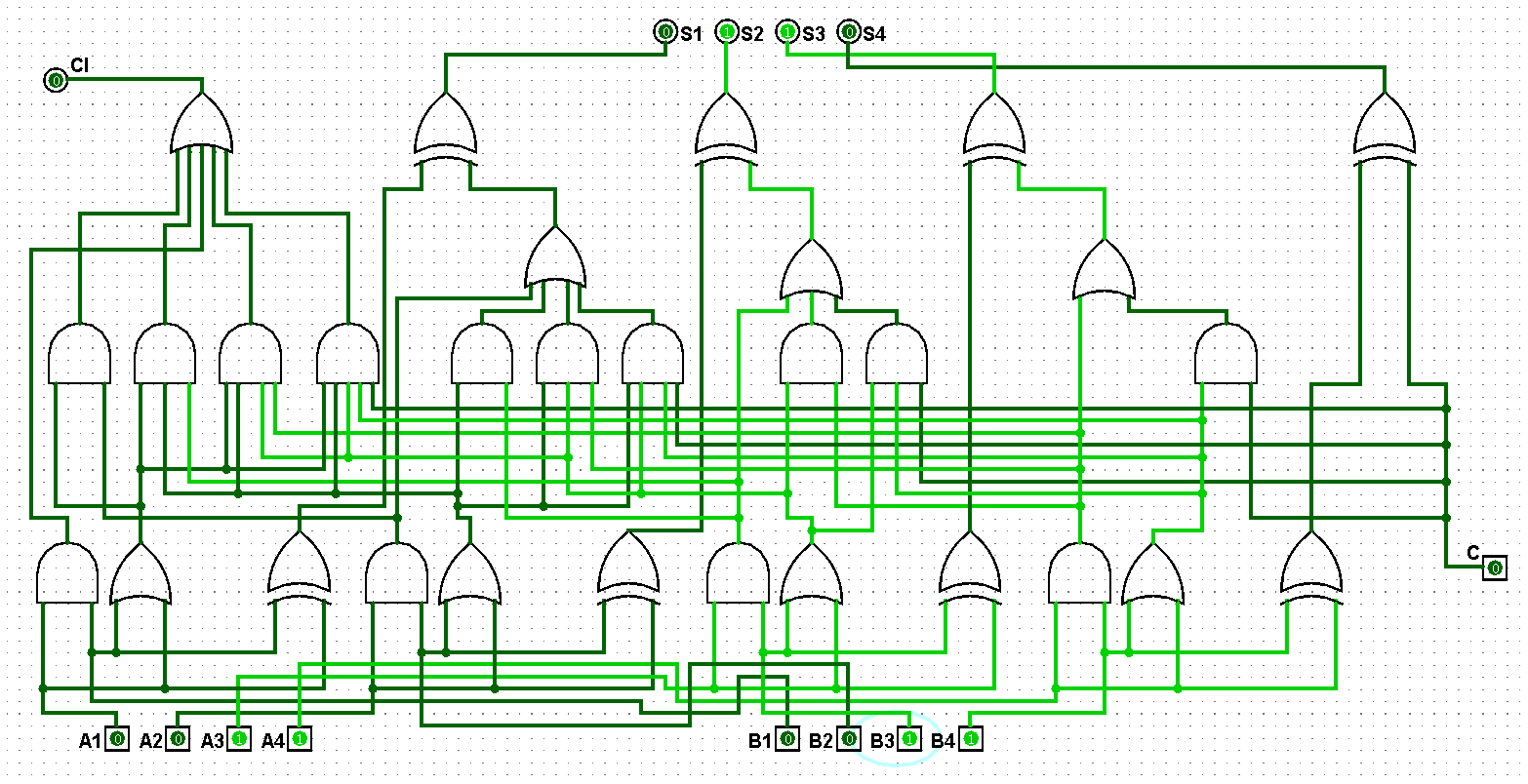
圖5-1-6 并行四位二進制全加器測試3+3=6

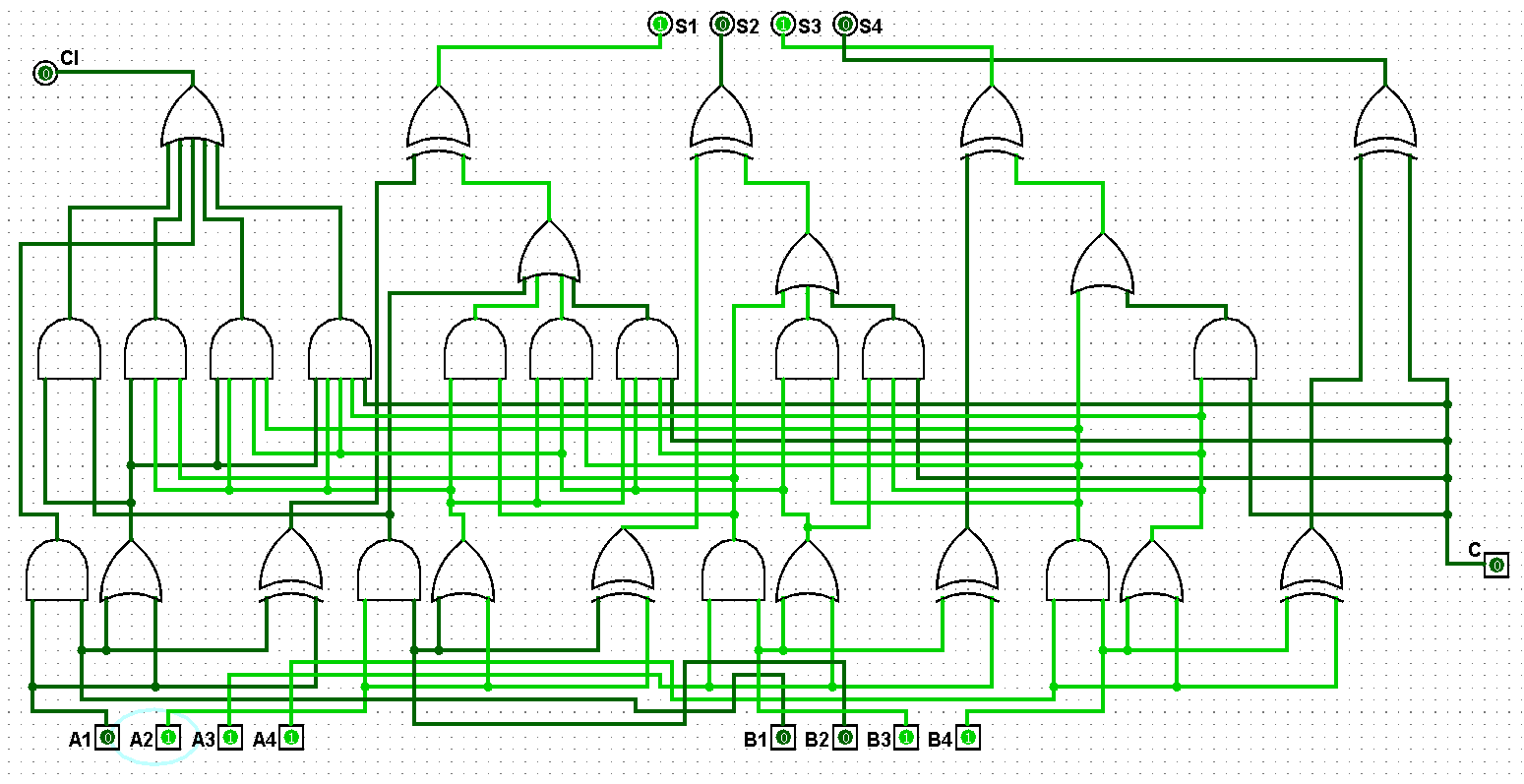
圖5-1-7 并行四位二進制全加器測試7+3=10

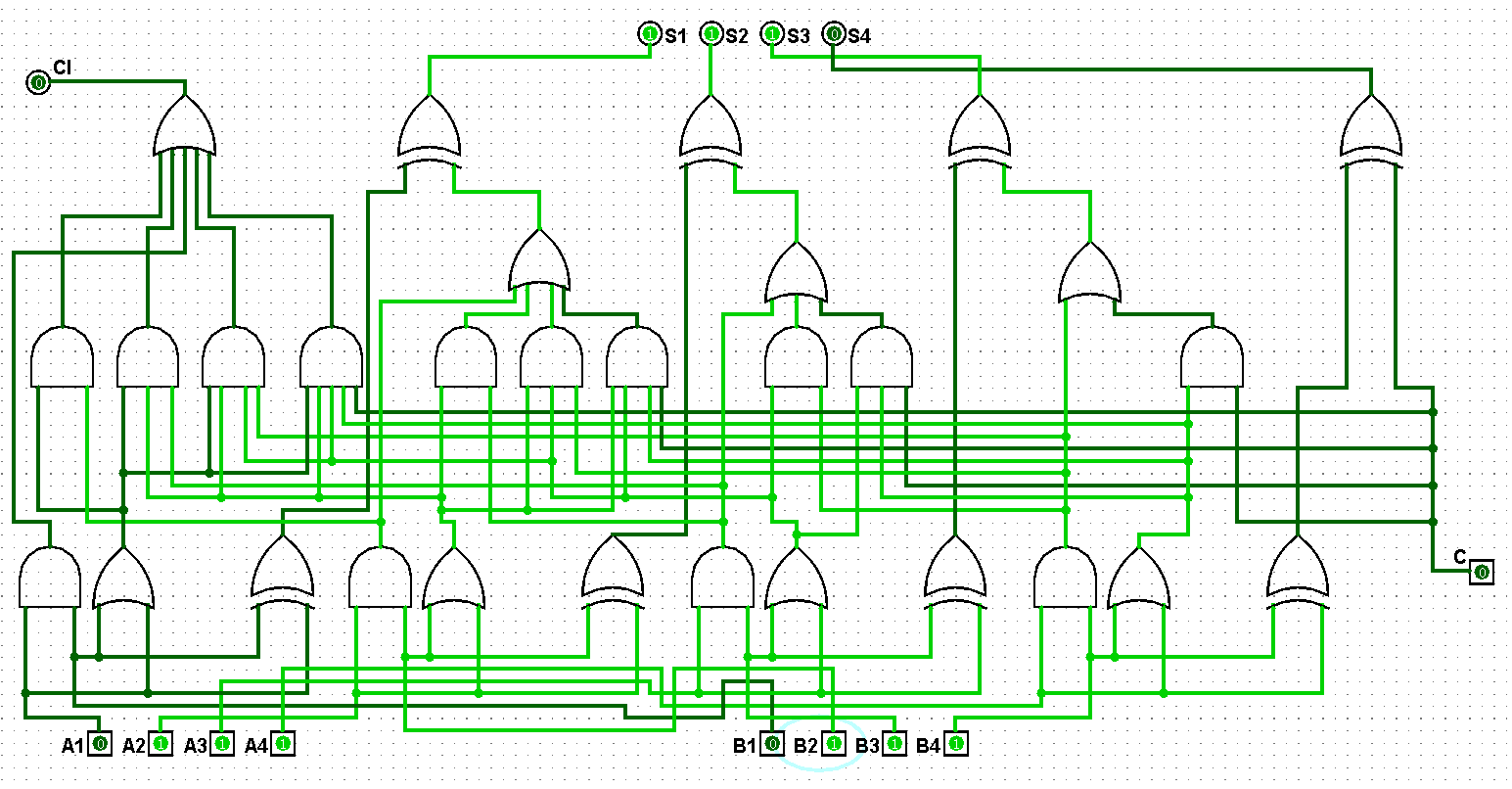
圖5-1-8 并行四位二進制全加器測試7+7=14

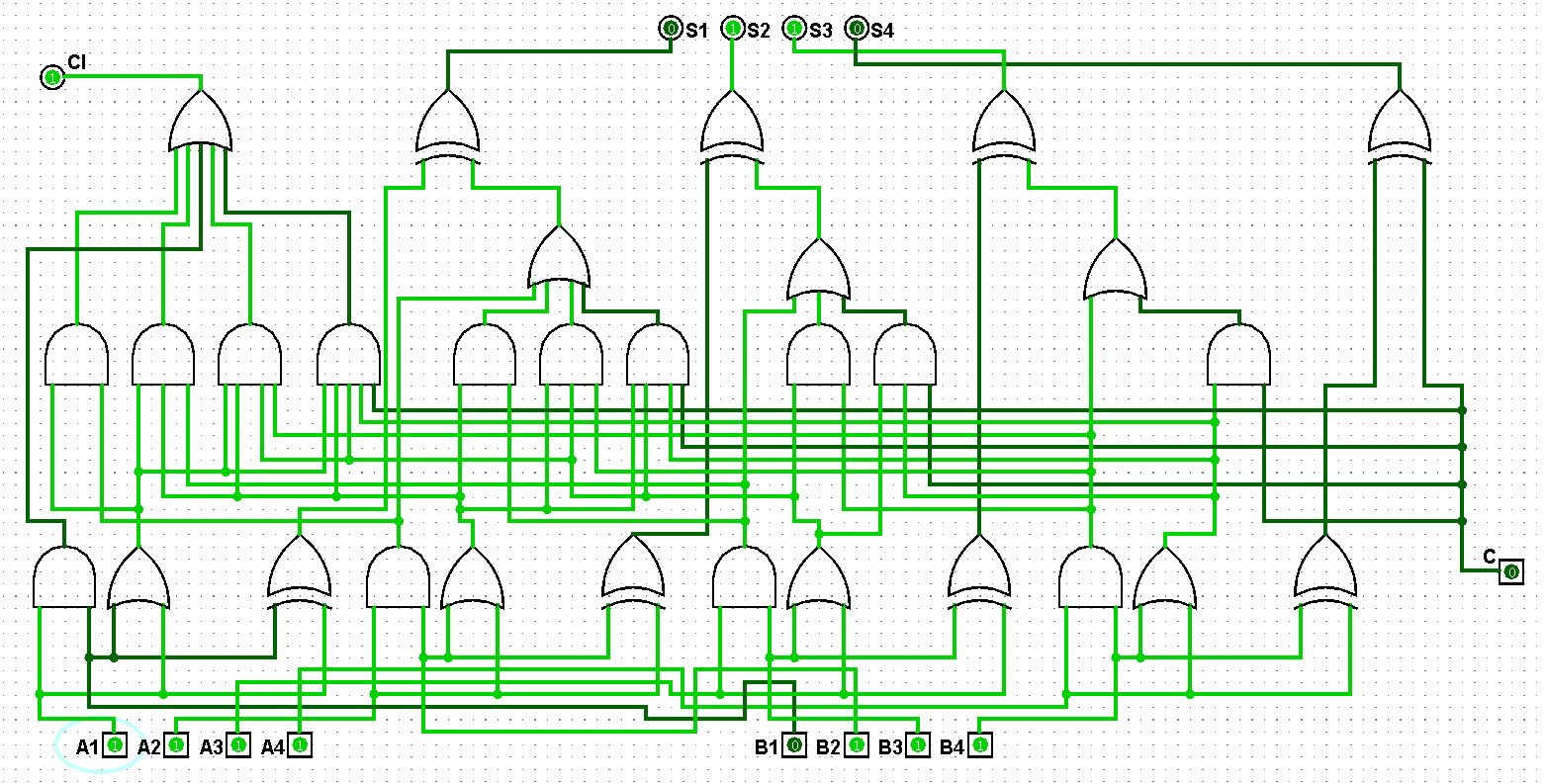
圖5-1-9 并行四位二進制全加器測試15+7=22

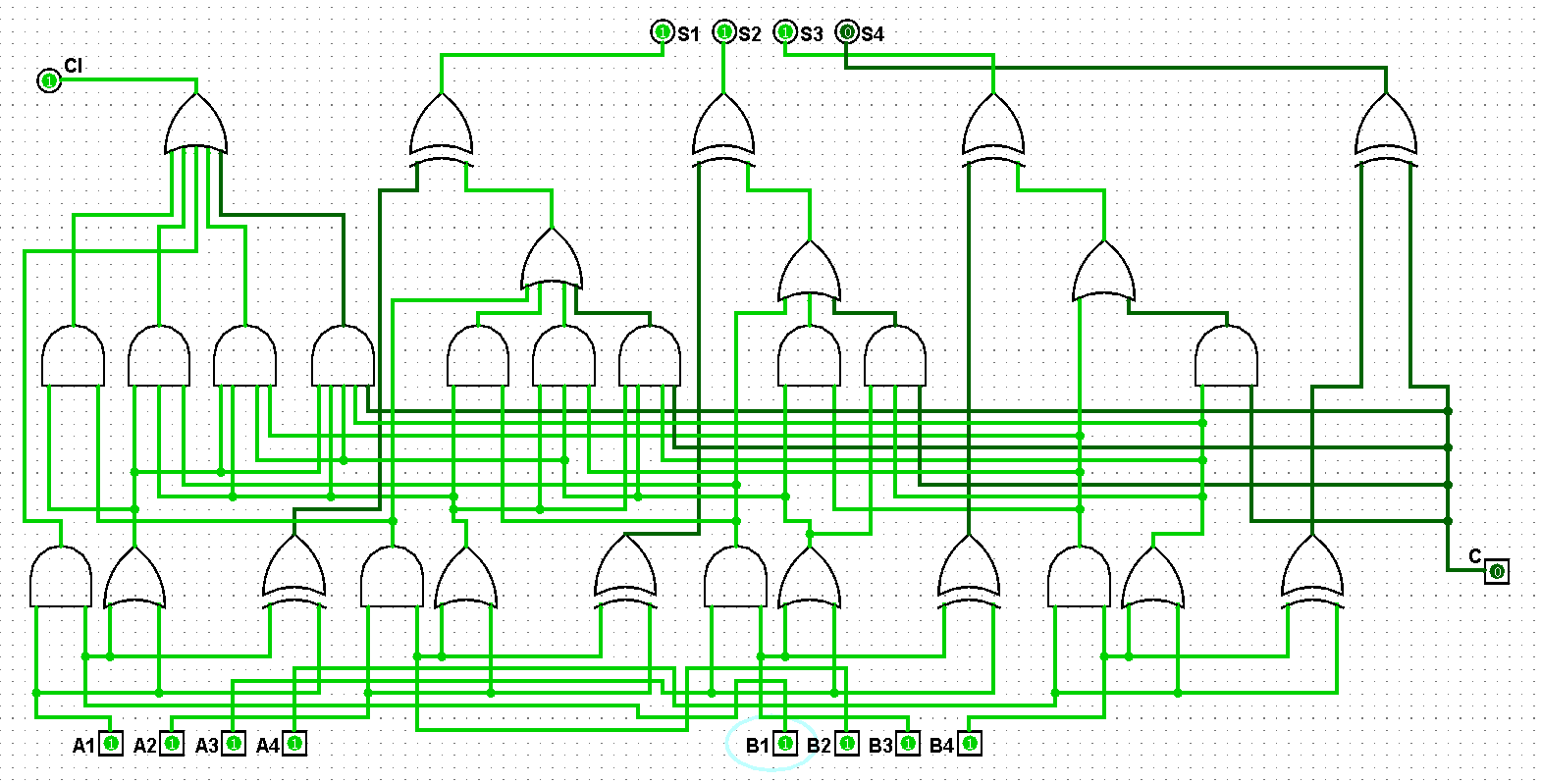
圖5-1-10 并行四位二進制全加器測試15+15=30

2、打開Logisim軟件，在第一步實現的并行四位二進制全加器的基礎上構建包括溢出、符號、歸零、進位等檢測功能的四位二進制運算器，鋪設完成后進行測試進而判斷電路是否鋪設成功。

????????（1）使用溢出邏輯公式OF=A’B’S+ABS’（A’、B’、S’分別表示對A、B、S進行非操作后的結果，S表示A和B進行運算的結果）完成對溢出功能的實現，當有效位的結果值全部為0時ZF=1,否則ZF=0；通過最高位的進位進行對符號和進位的判斷，如果是0表示為+并沒有進位，否則為-并進行了進位（OF表示溢出標志，ZF表示零標志，SF表示符號標志，CF表示進位標志），對應的部分四位二進制運算器邏輯電路真值表如圖5-2-1所示：

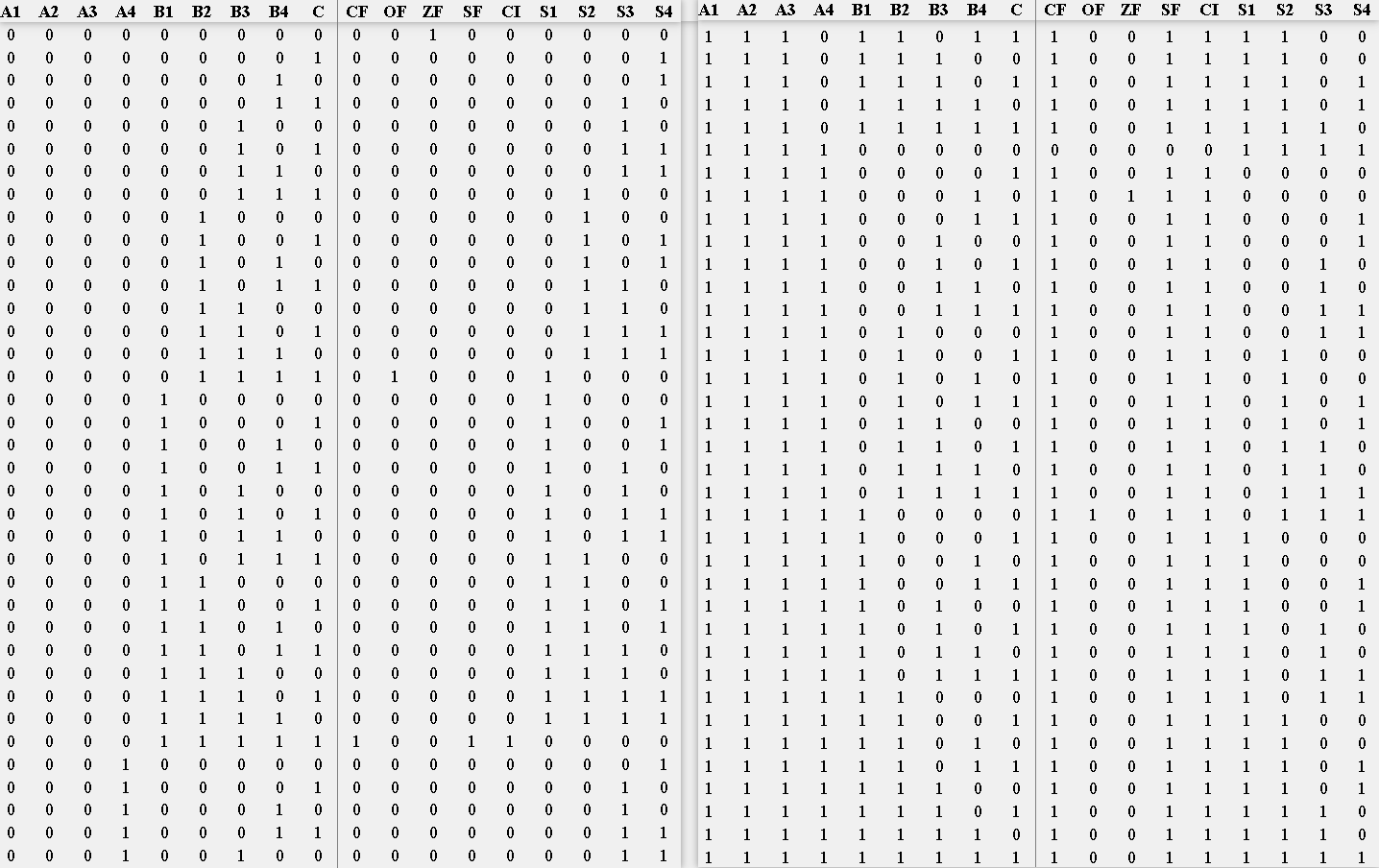
圖5-2-1 四位二進制運算器邏輯電路真值表

????????（2）依據邏輯公式完成四位二進制運算器邏輯電路的架構，將最高位A4、B4分別進行非操作后和S4進行與操作，再將S進行非操作后和A4、B4進行與操作，最后將兩個結果進行或操作得到溢出標志OF；將輸出值S1、S2、S3、S4進行或非操作后得到零標志ZF；通過最高位的進位得到符號標志SF和進位標志CF，對應的四位二進制運算器邏輯電路如圖5-2-2所示：

圖5-2-2 四位二進制運算器邏輯電路

????????（3）四位二進制運算器邏輯電路鋪設完畢后進行測試，進而判斷自己的電路是否鋪設成功，經過測試后此電路狀態一切正常，對應的四位二進制運算器邏輯電路測試如圖5-2-3至5-2-11所示：

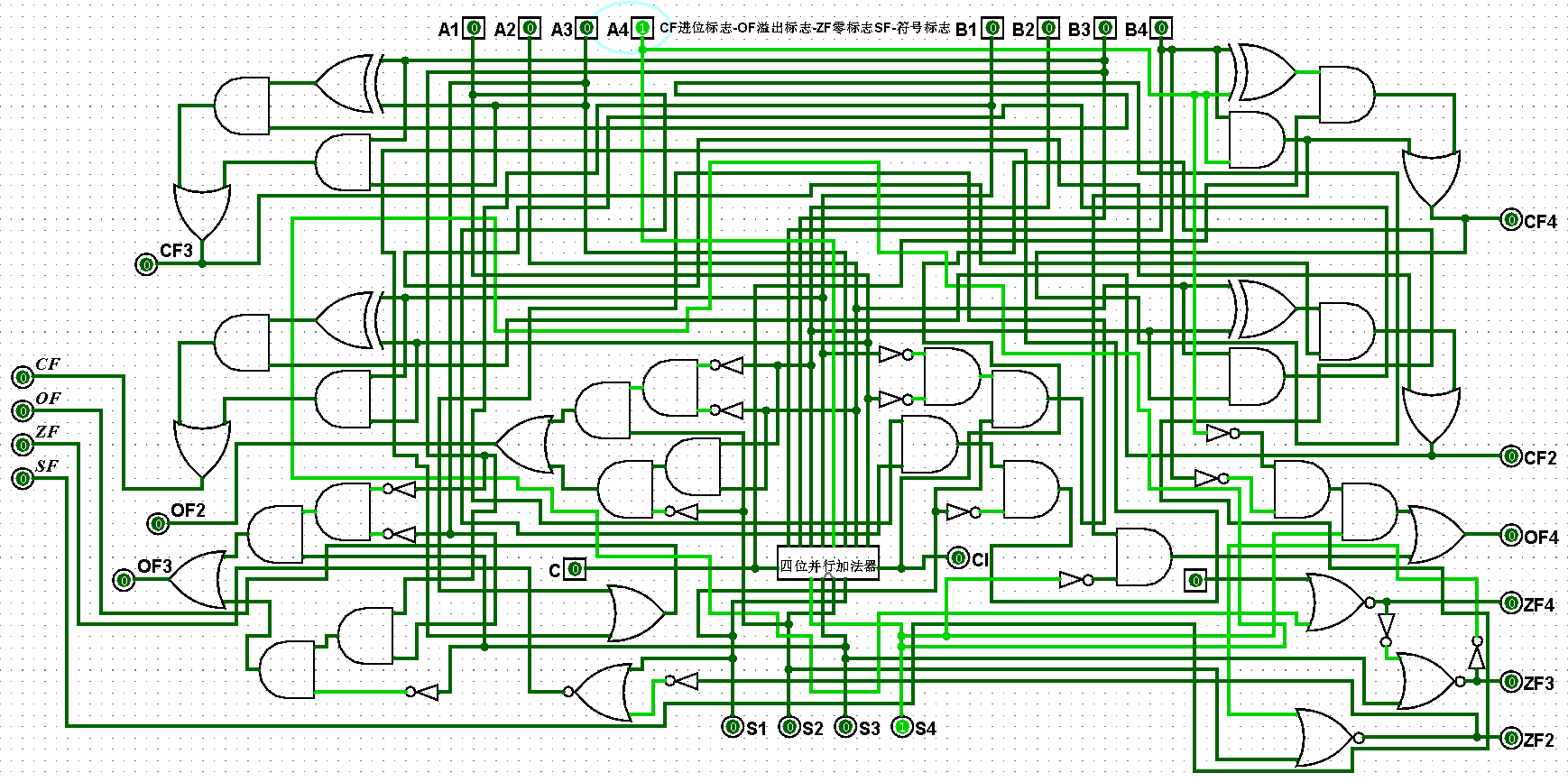
圖5-2-3 四位二進制運算器測試1+0=1,CF=0,OF=0,ZF=0,SF=0

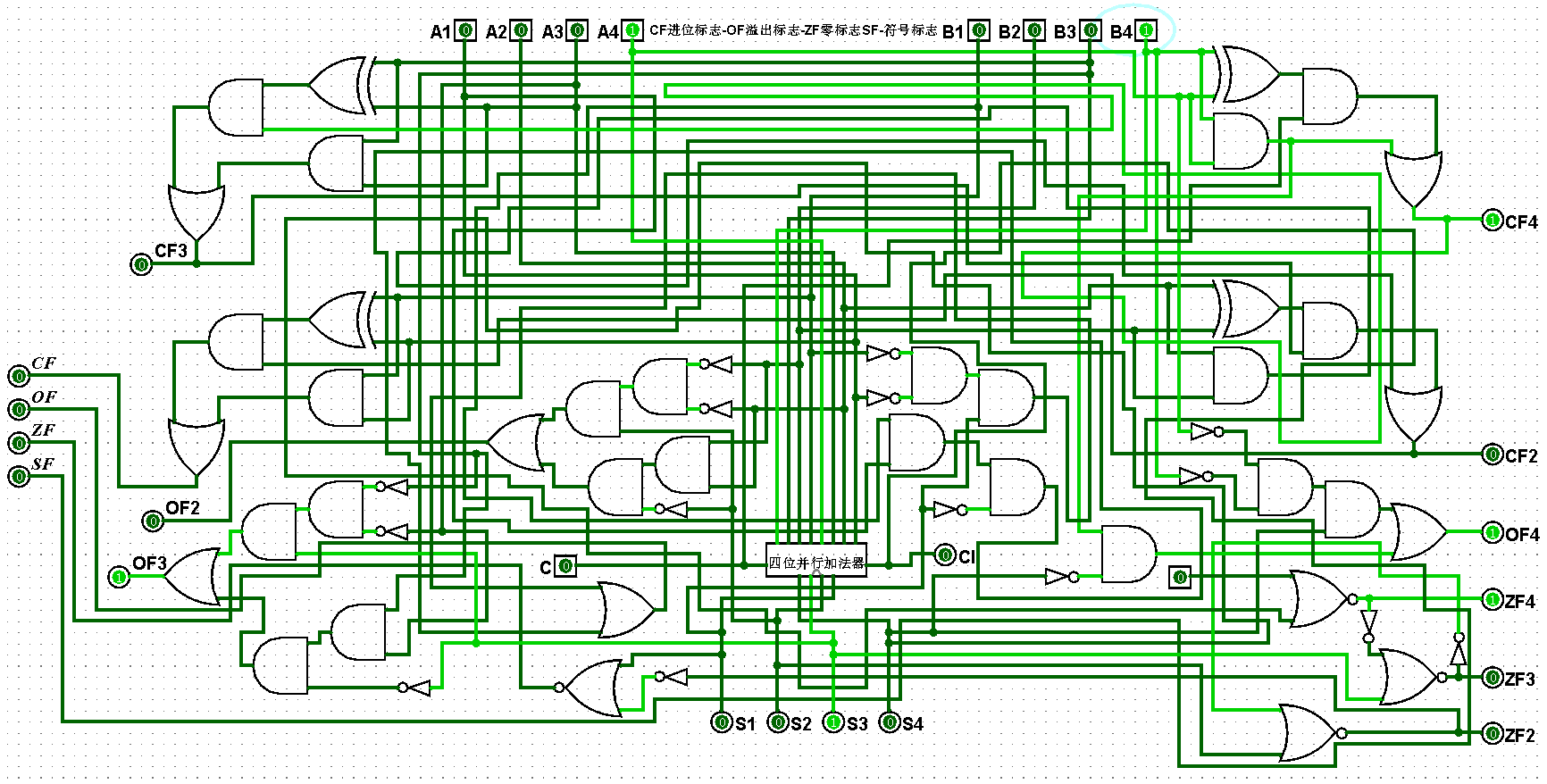
圖5-2-4 四位二進制運算器測試1+1=2,CF=0,OF=0,ZF=0,SF=0

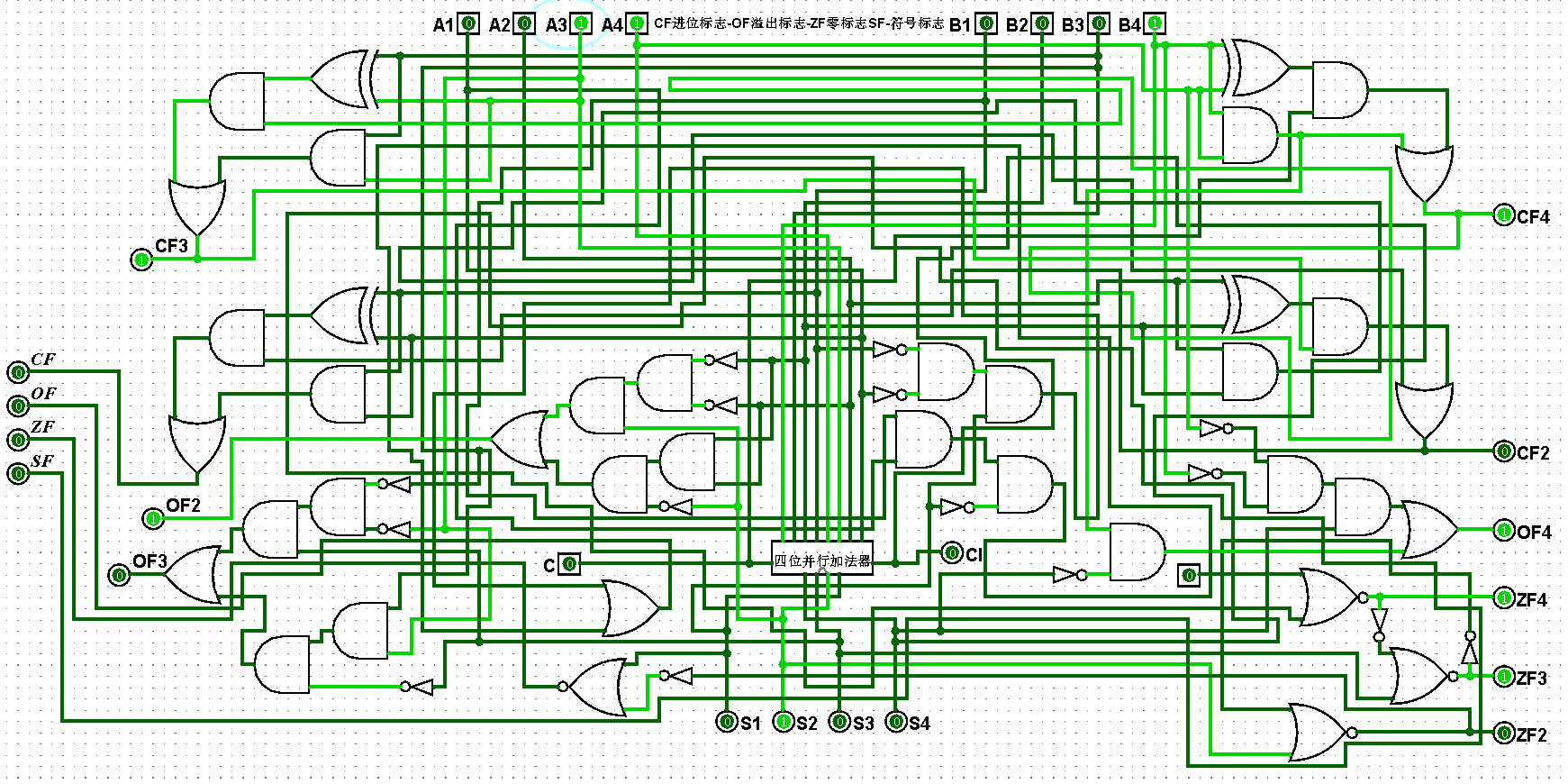
圖5-2-5 四位二進制運算器測試3+1=4,CF=0,OF=0,ZF=0,SF=0

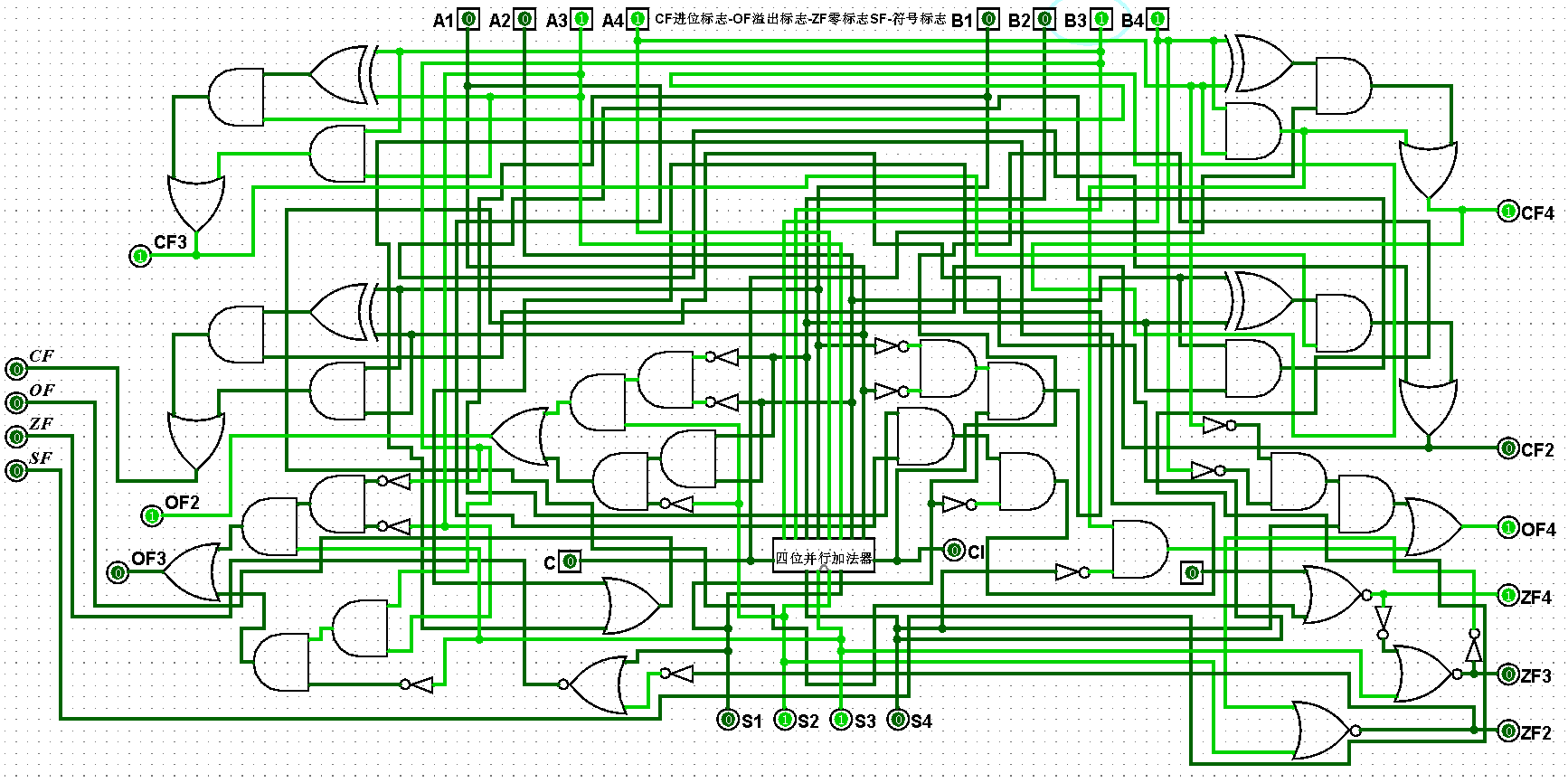
圖5-2-6 四位二進制運算器測試3+3=6,CF=0,OF=0,ZF=0,SF=0

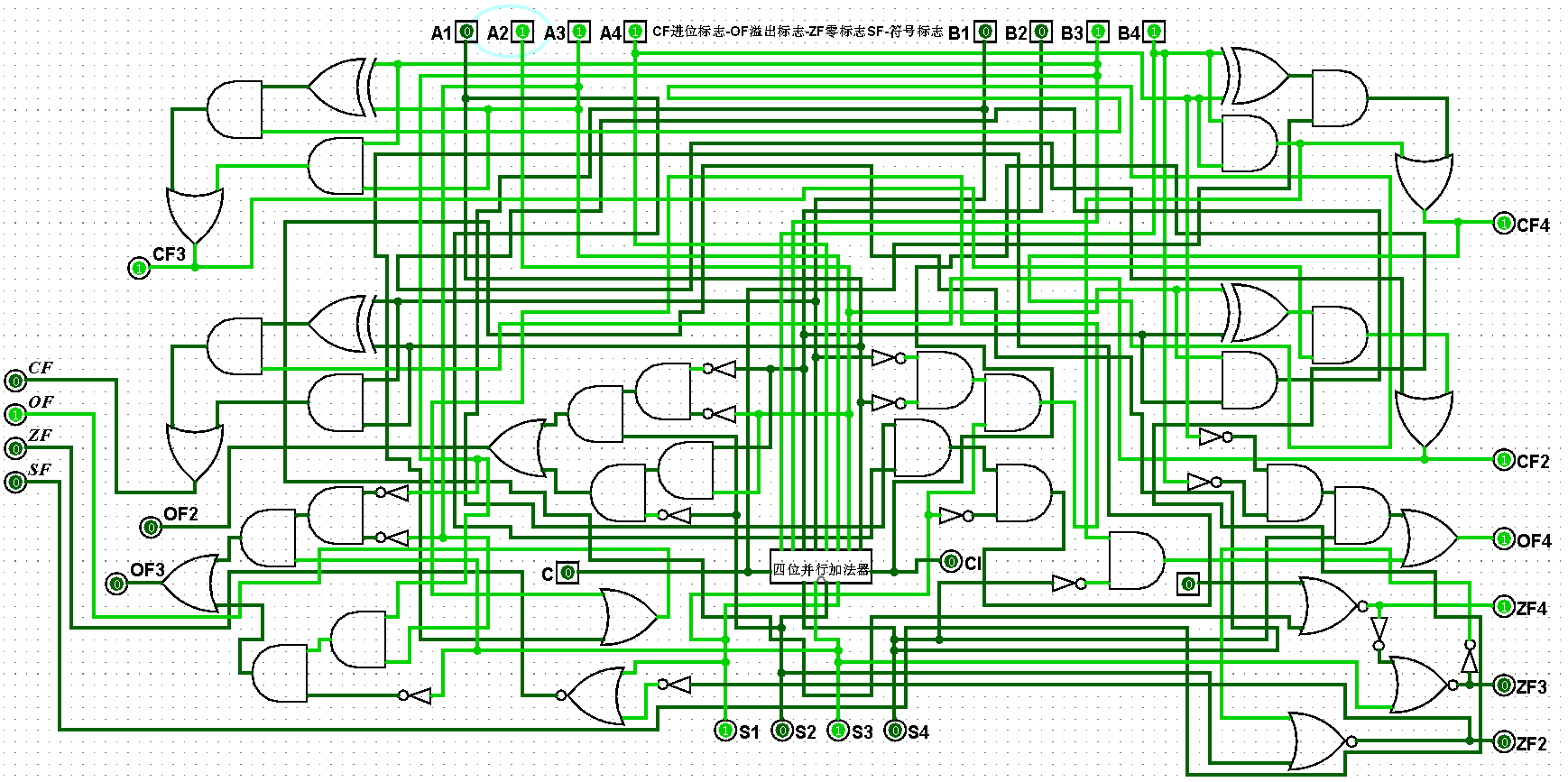
圖5-2-7 四位二進制運算器測試7+3=10,CF=0,OF=1,ZF=0,SF=0

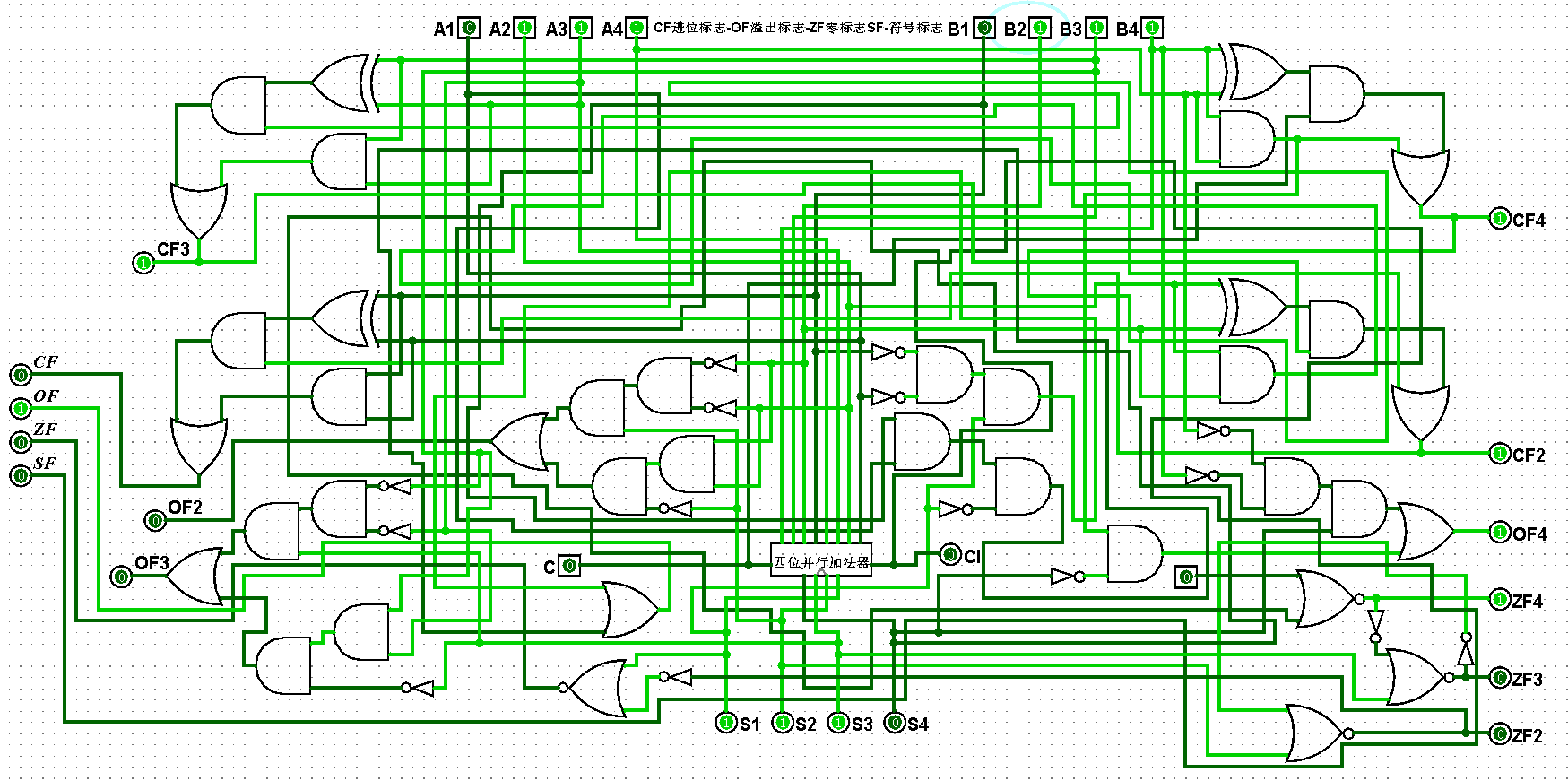
圖5-2-8 四位二進制運算器測試7+7=14,CF=0,OF=1,ZF=0,SF=0

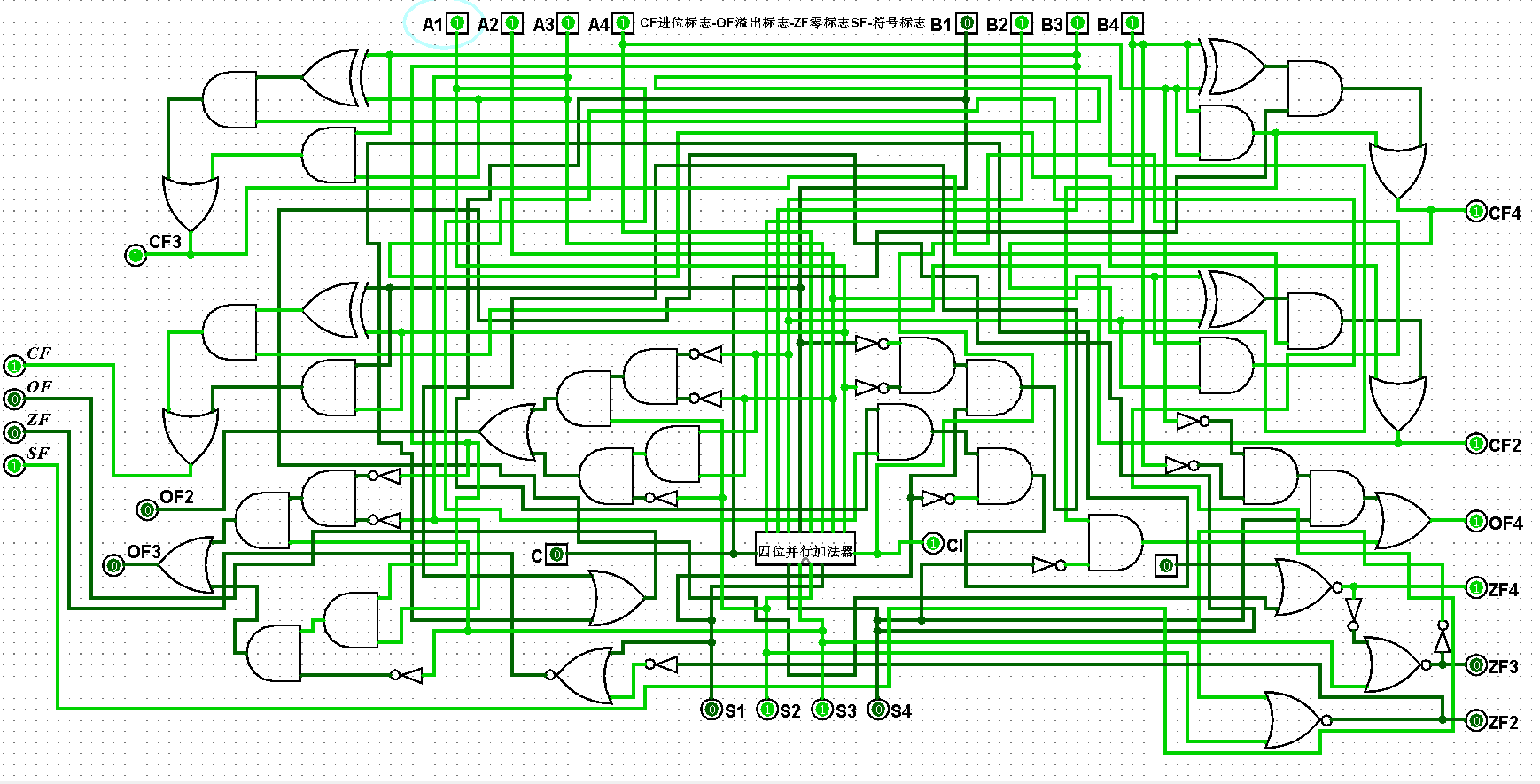
圖5-2-9 四位二進制運算器測試15+7=22,CF=1,OF=0,ZF=0,SF=1

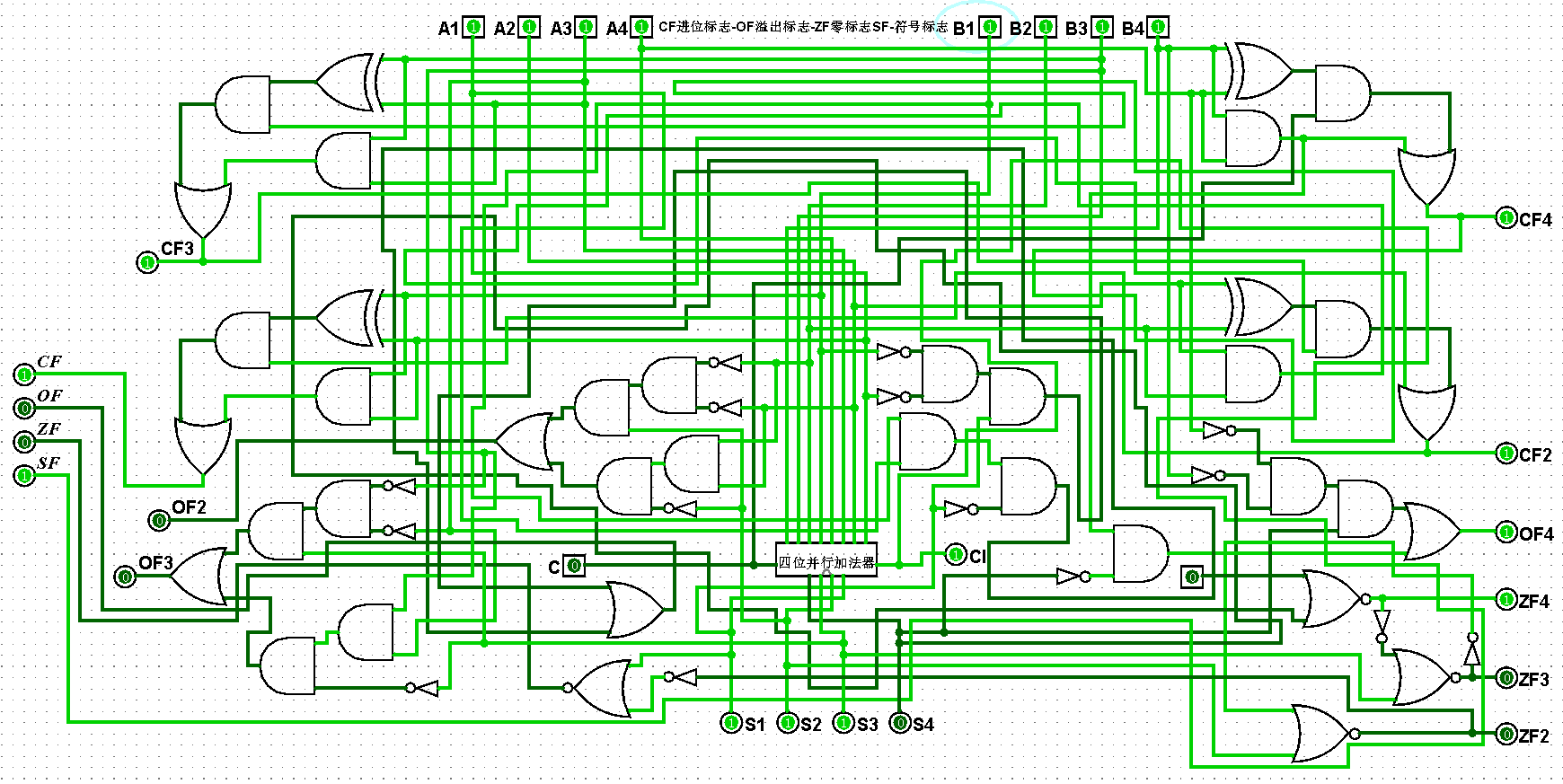
圖5-2-10 四位二進制運算器測試15+15=30,CF=1,OF=0,ZF=0,SF=1

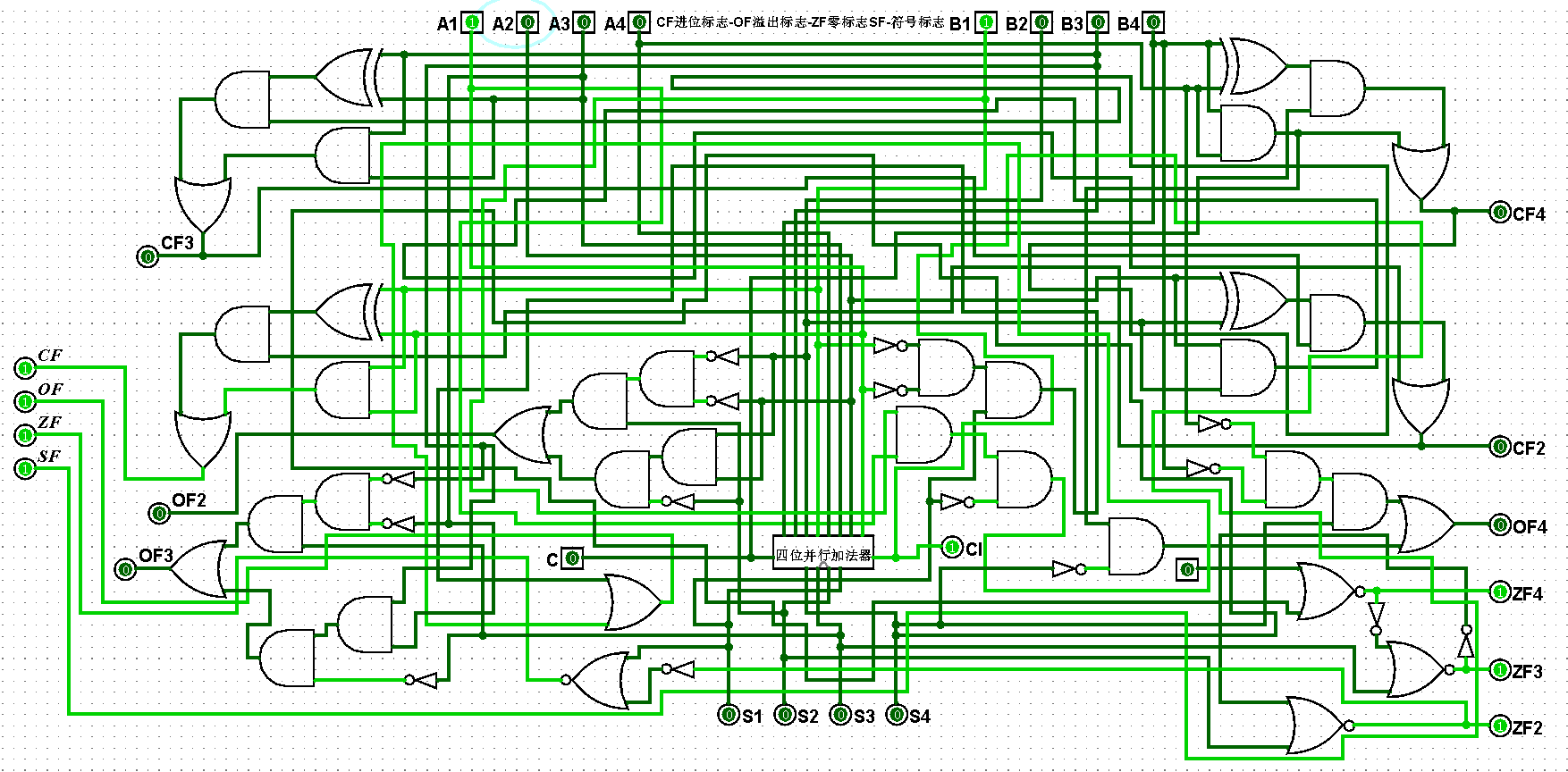
圖5-2-11 四位二進制運算器測試8+8=16,CF=1,OF=1,ZF=1,SF=1

3、打開Logisim軟件，利用兩個四位二進制加法器實現八位串行加法器，列出八位串行加法器邏輯電路真值表，并使用兩個四位二進制加法器實現八位串行加法器邏輯電路，鋪設完成后進行測試進而判斷電路是否鋪設成功。

????????（1）通過低位的高位進位是高位的低位進位的方式搭建八位串行加法器，將低位的高位進位輸入到高位的低位進位上實現八位串行加法器的邏輯電路，對應的部分八位串行加法器邏輯電路真值表如圖5-3-1所示：

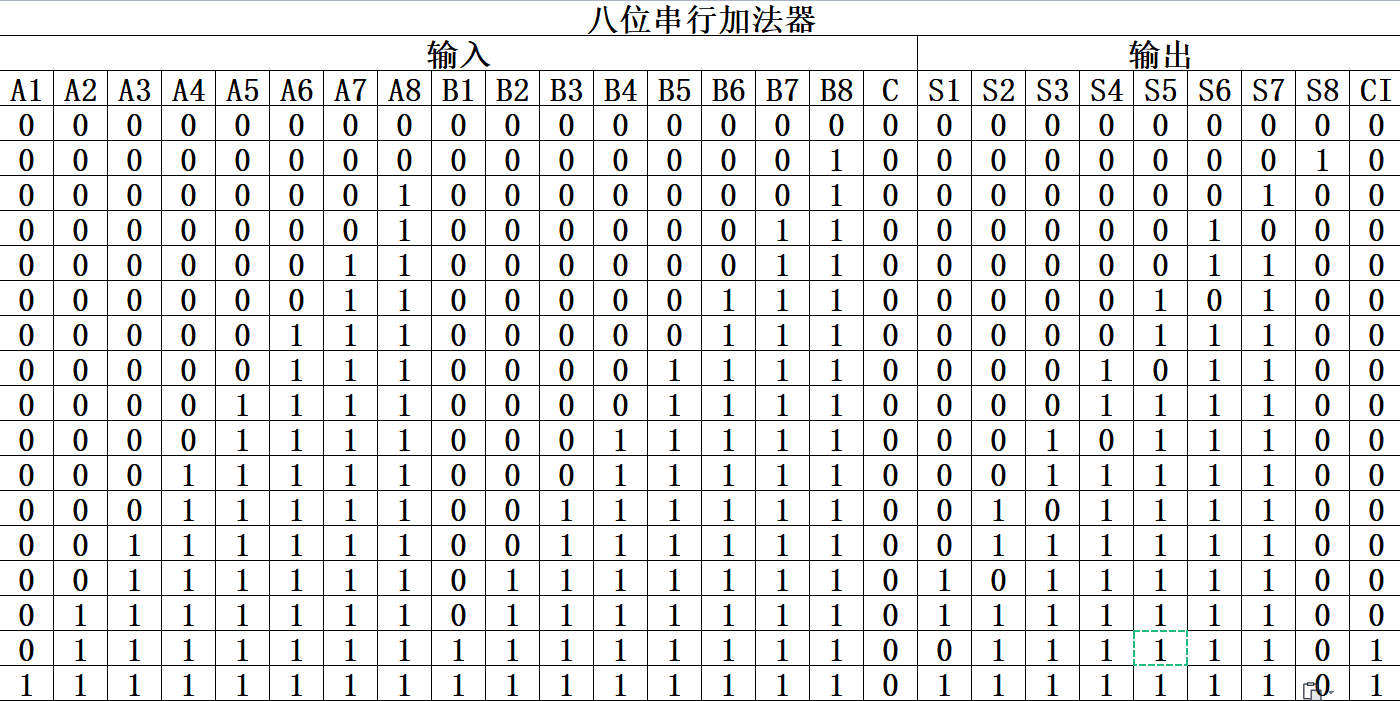
圖5-3-1 八位串行加法器邏輯電路真值表

????????（2）依據邏輯原理完成八位串行加法器邏輯電路的架構，在運行過程中低位的高位進位是高位的低位進位，將對應的進位進行構連即可實現八位串行加法器，對應的八位串行加法器邏輯電路如圖5-3-2至5-3-18所示：

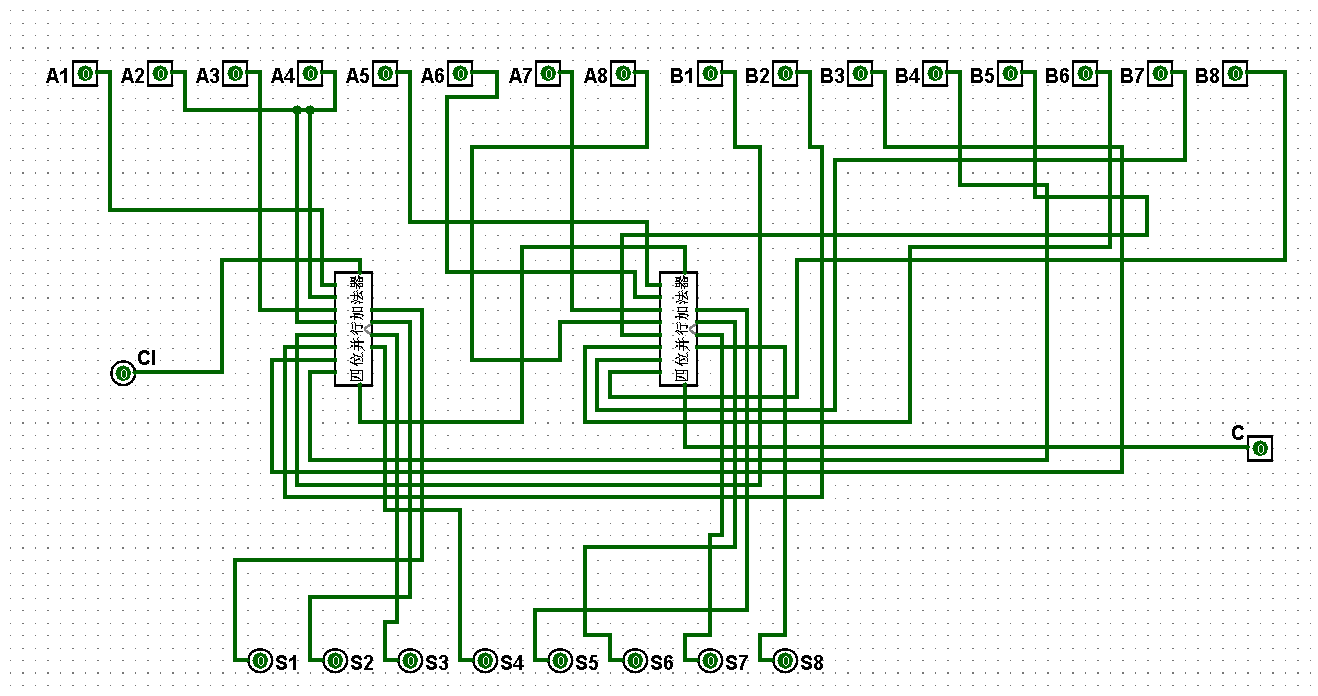
圖5-3-2 八位串行加法器邏輯電路

????????（3）八位串行加法器邏輯電路鋪設完畢后進行測試，進而判斷自己的電路是否鋪設成功，經過測試后此電路狀態一切正常，對應的八位串行加法器邏輯電路測試如圖5-3-3至5-3-18所示：

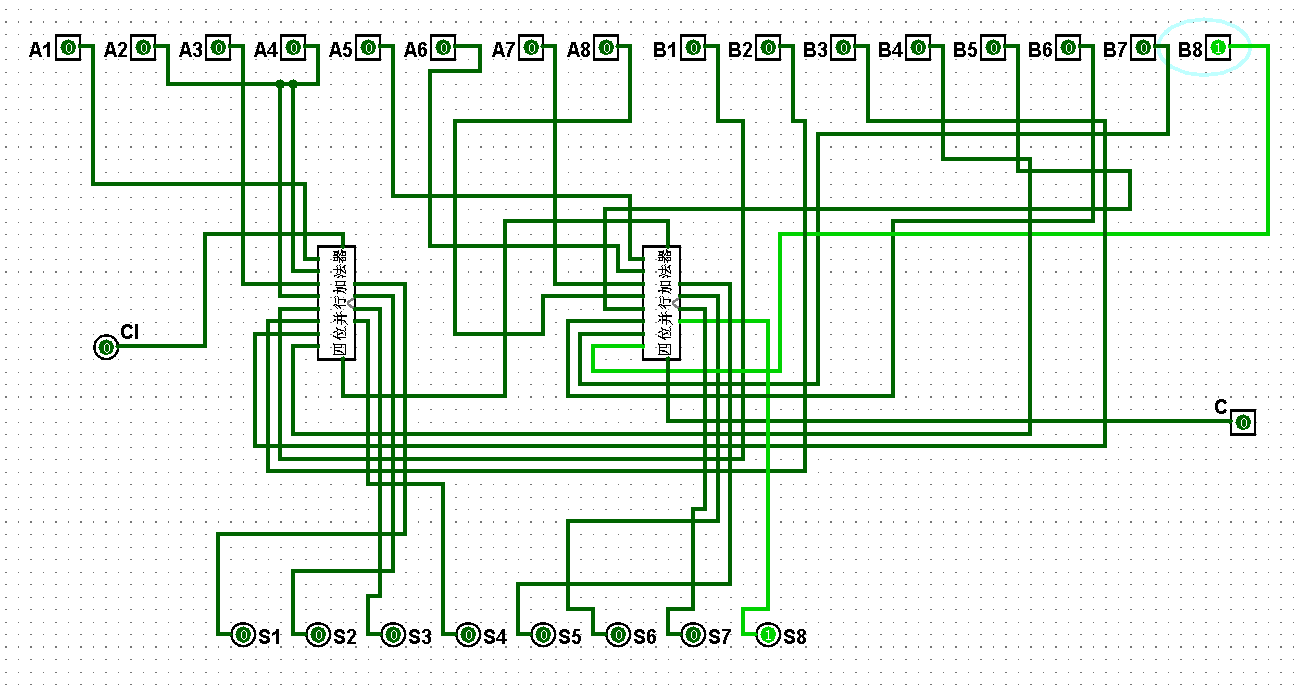
圖5-3-3 八位串行加法器測試0+1=1

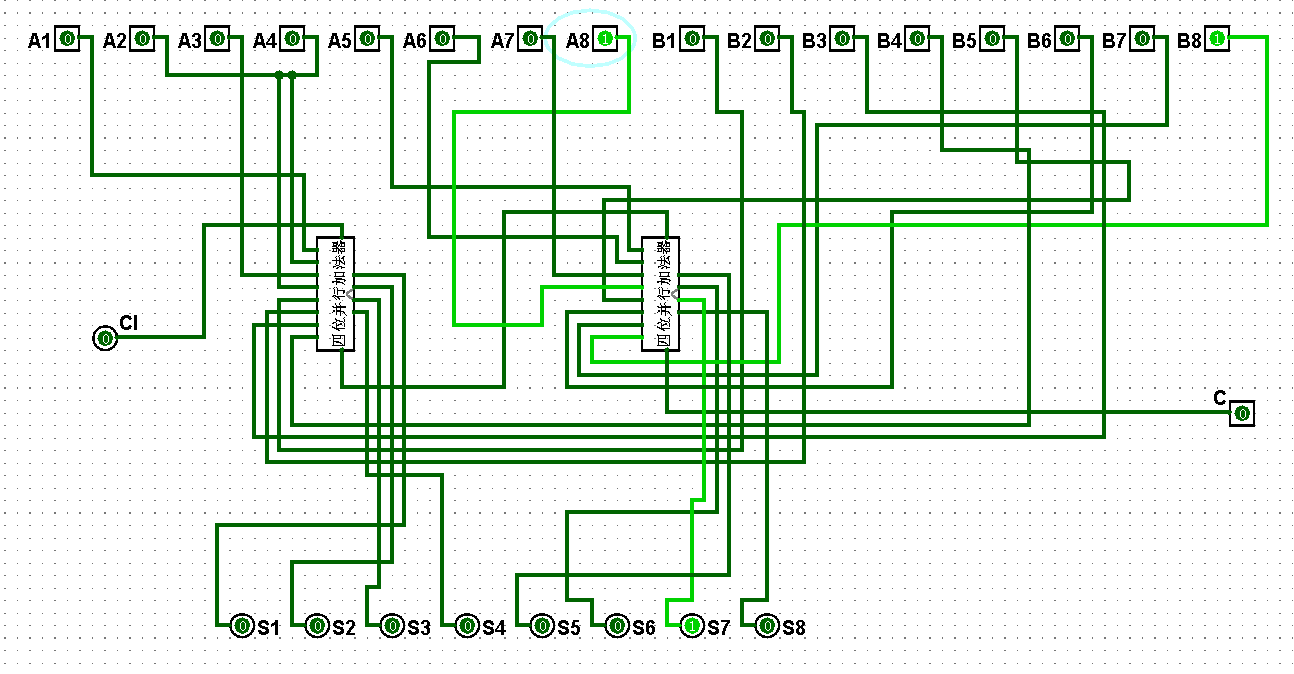
圖5-3-4 八位串行加法器測試1+1=2

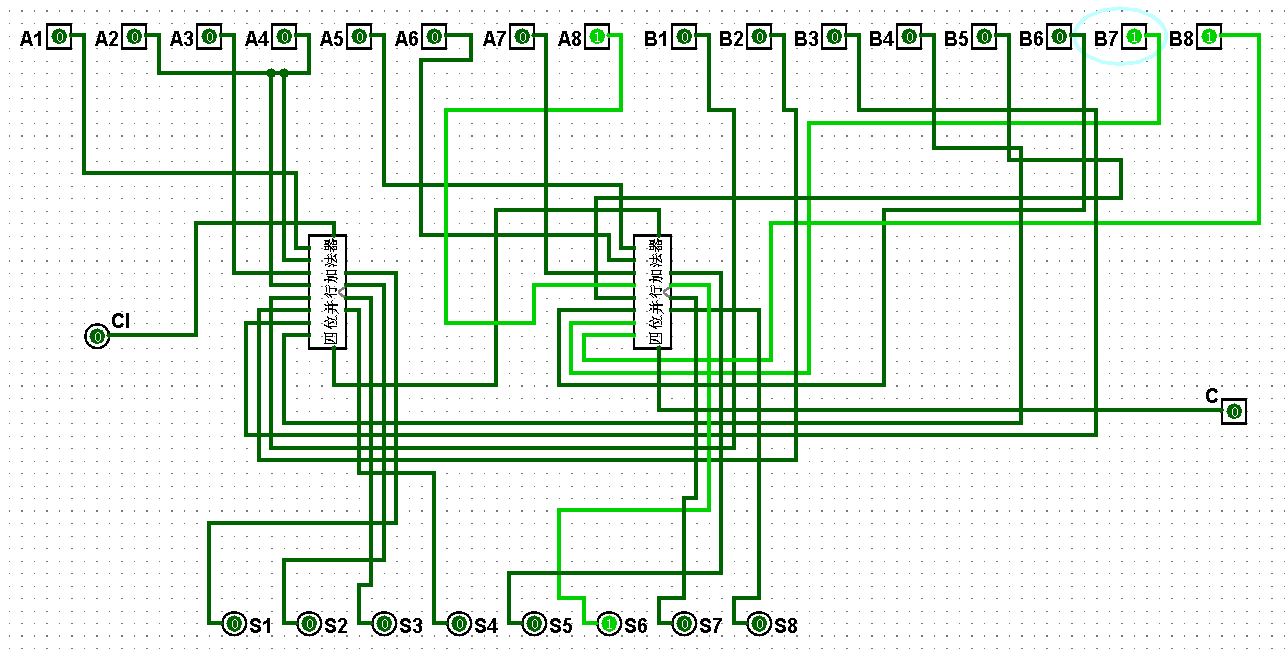
圖5-3-5 八位串行加法器測試1+3=4

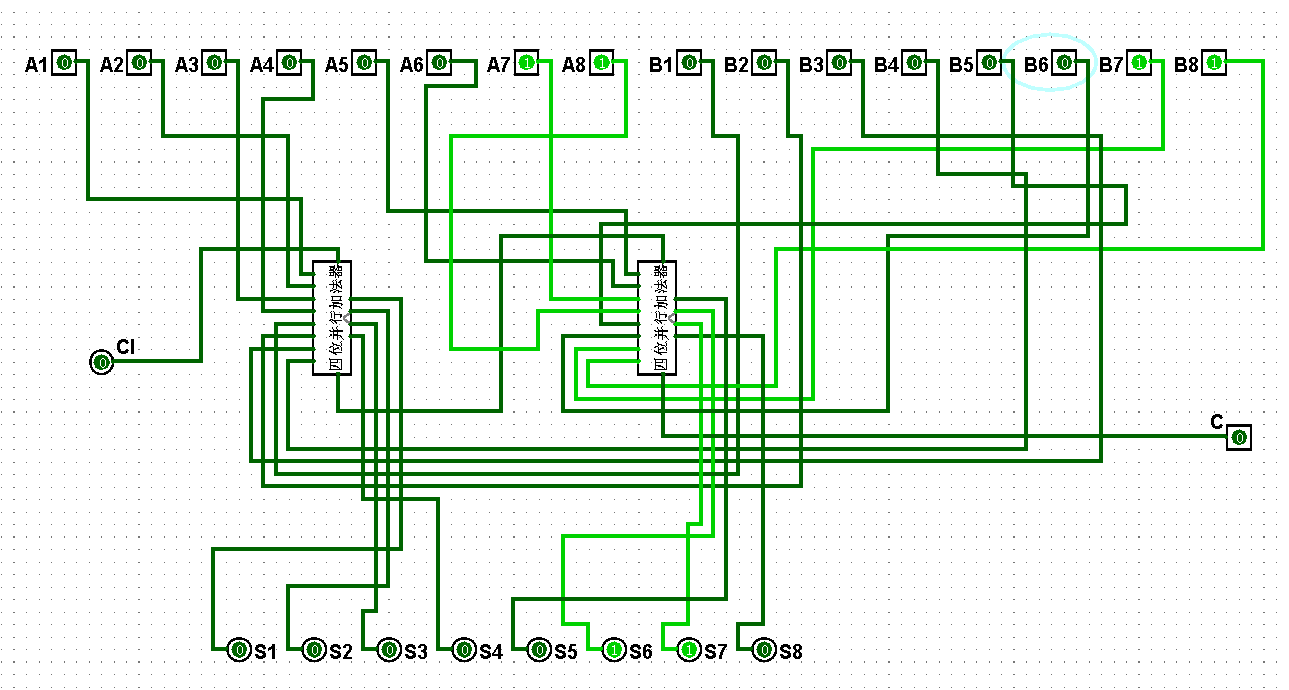
圖5-3-6 八位串行加法器測試3+3=6

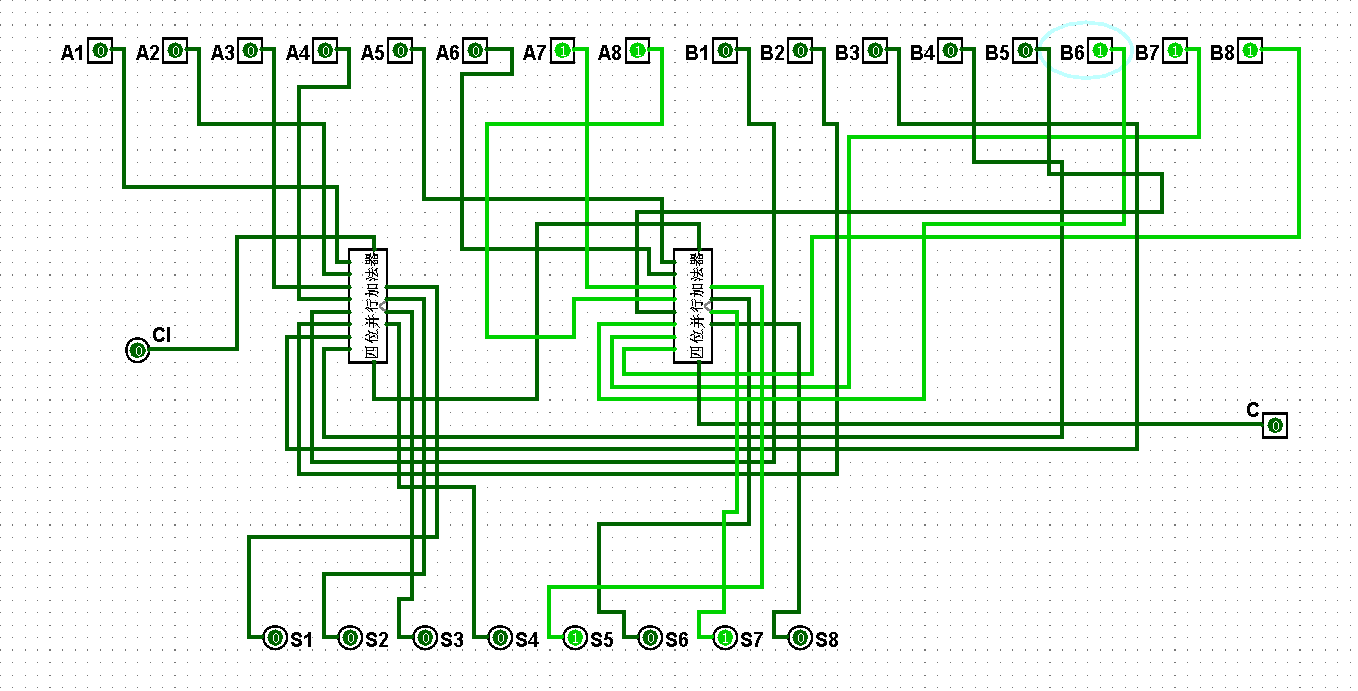
圖5-3-7 八位串行加法器測試3+7=10

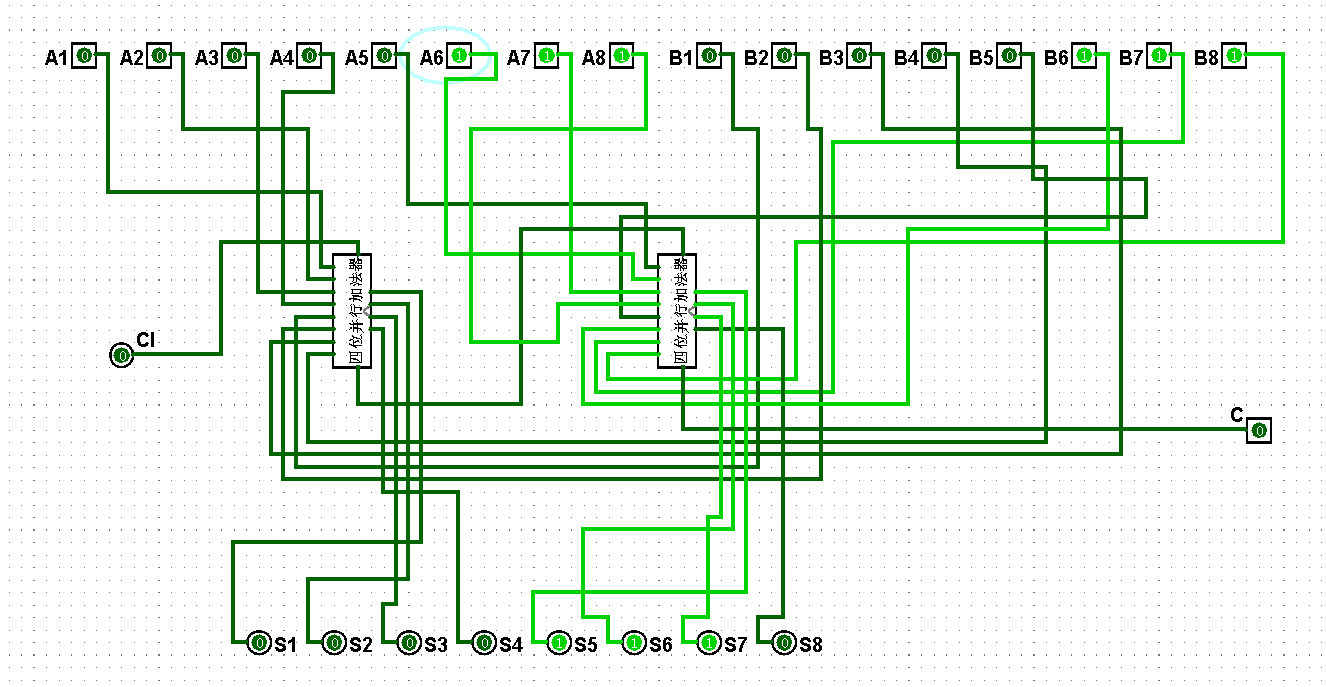
圖5-3-8 八位串行加法器測試7+7=14

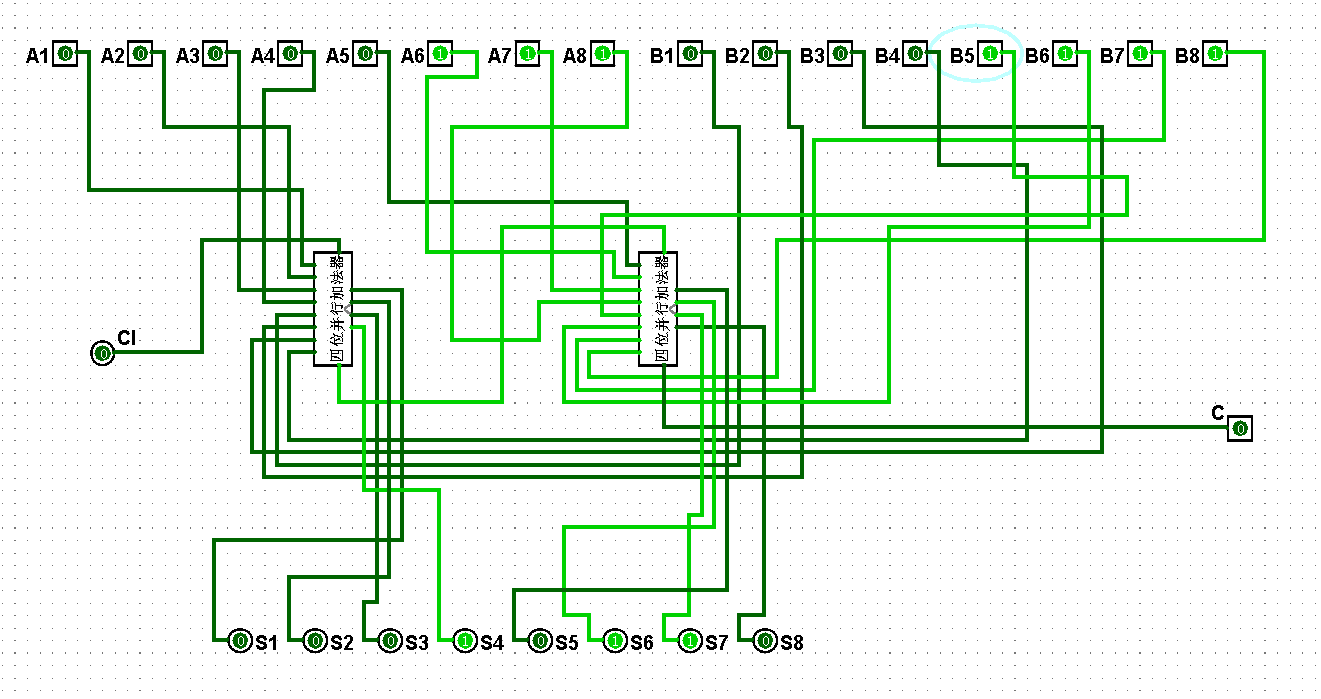
圖5-3-9 八位串行加法器測試7+15=22

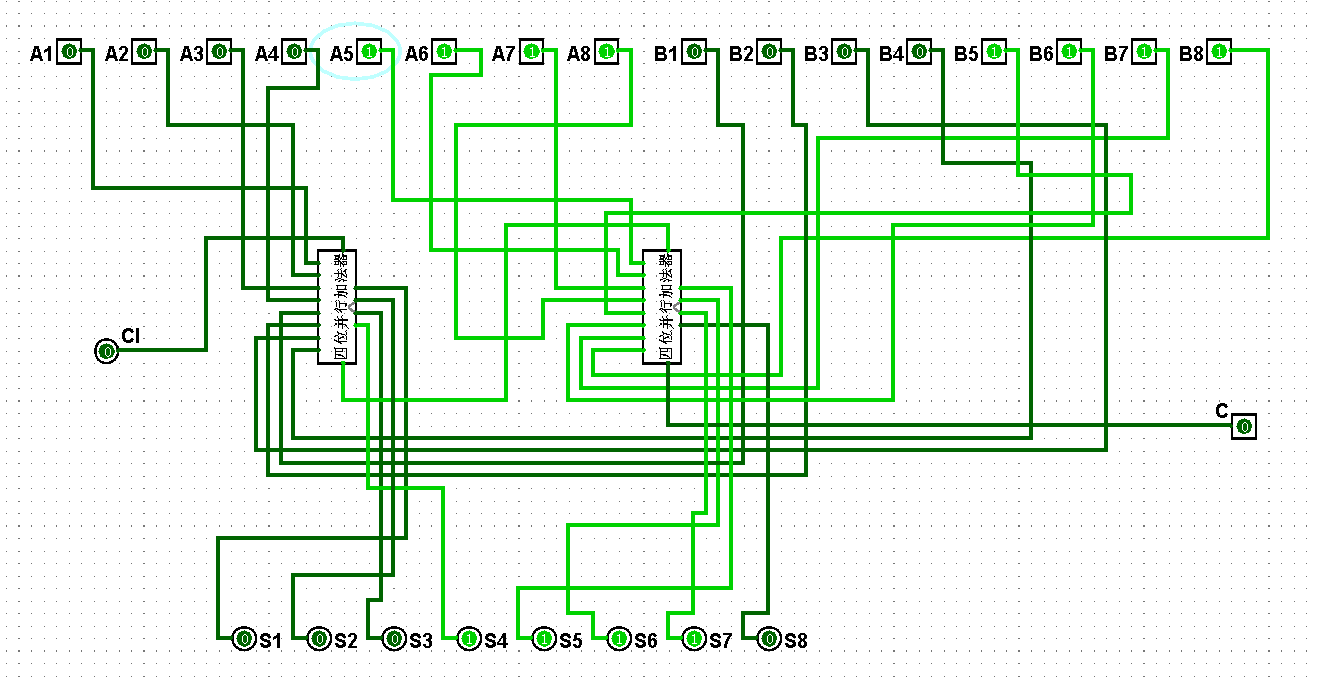
圖5-3-10 八位串行加法器測試15+15=30

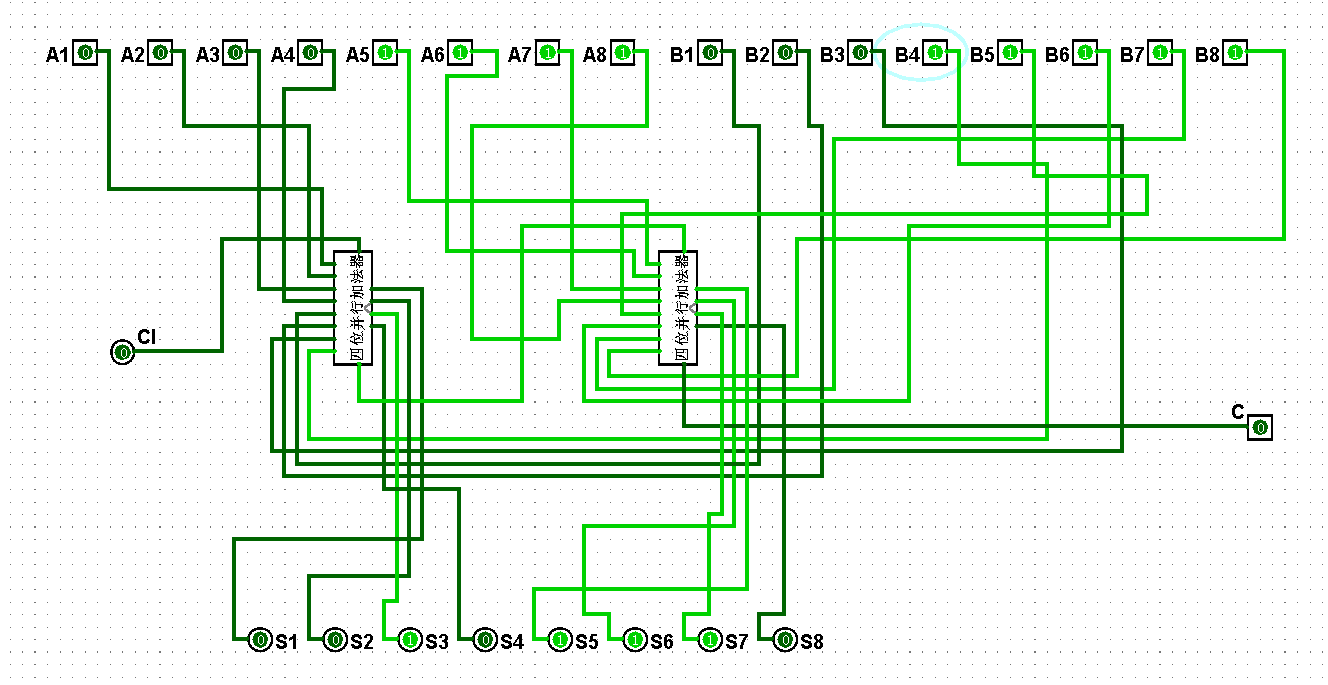
圖5-3-11 八位串行加法器測試15+31=46

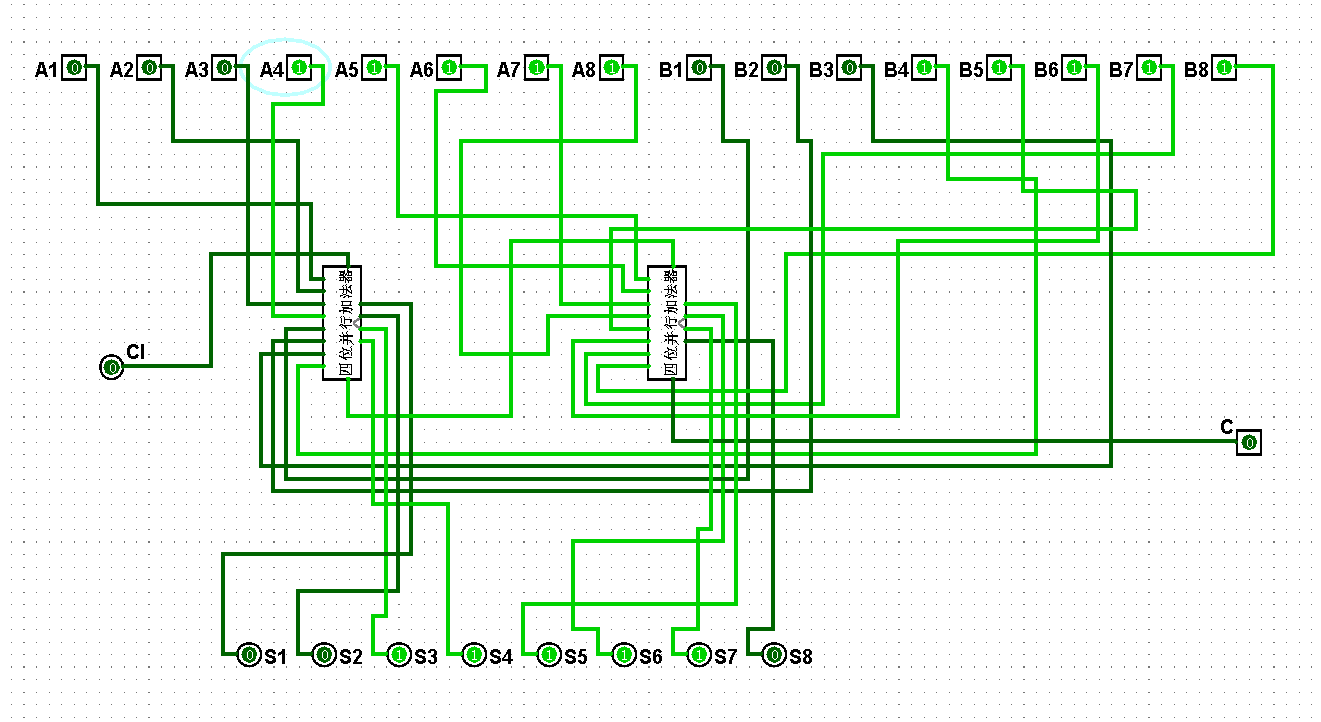
圖5-3-12 八位串行加法器測試31+31=62

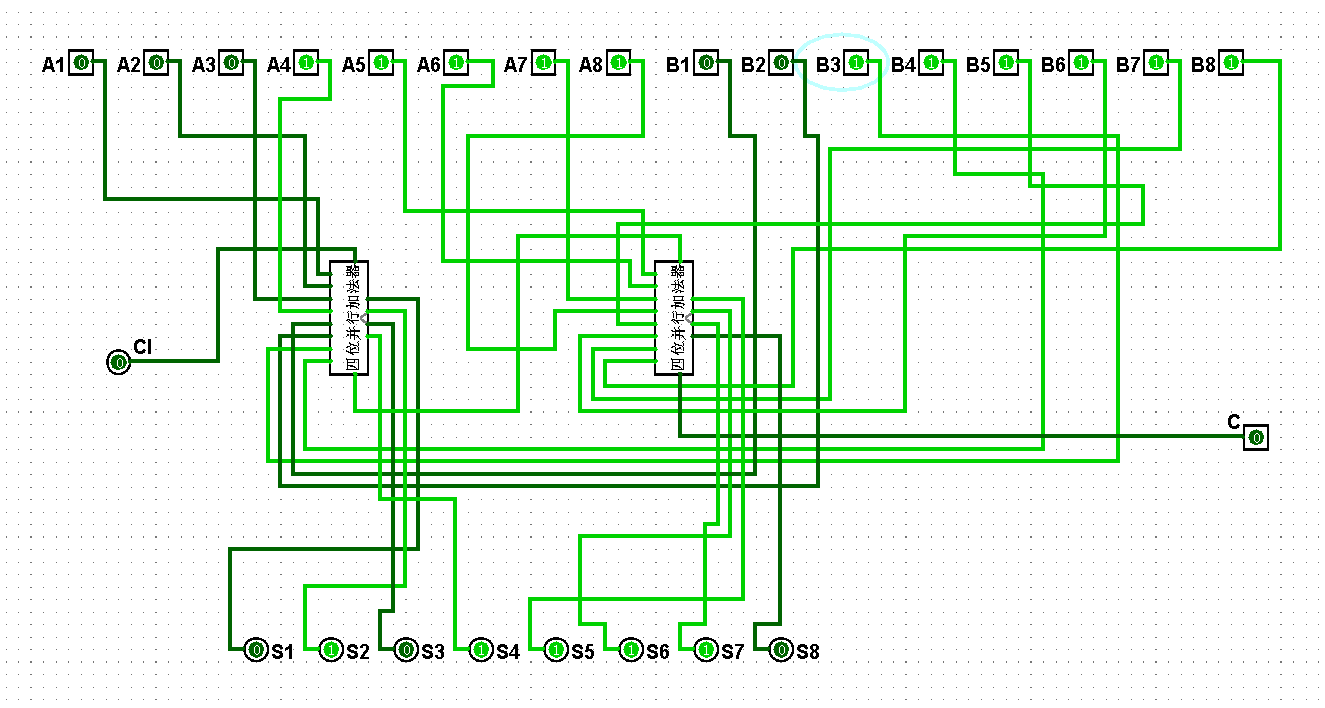
圖5-3-13 八位串行加法器測試31+63=94

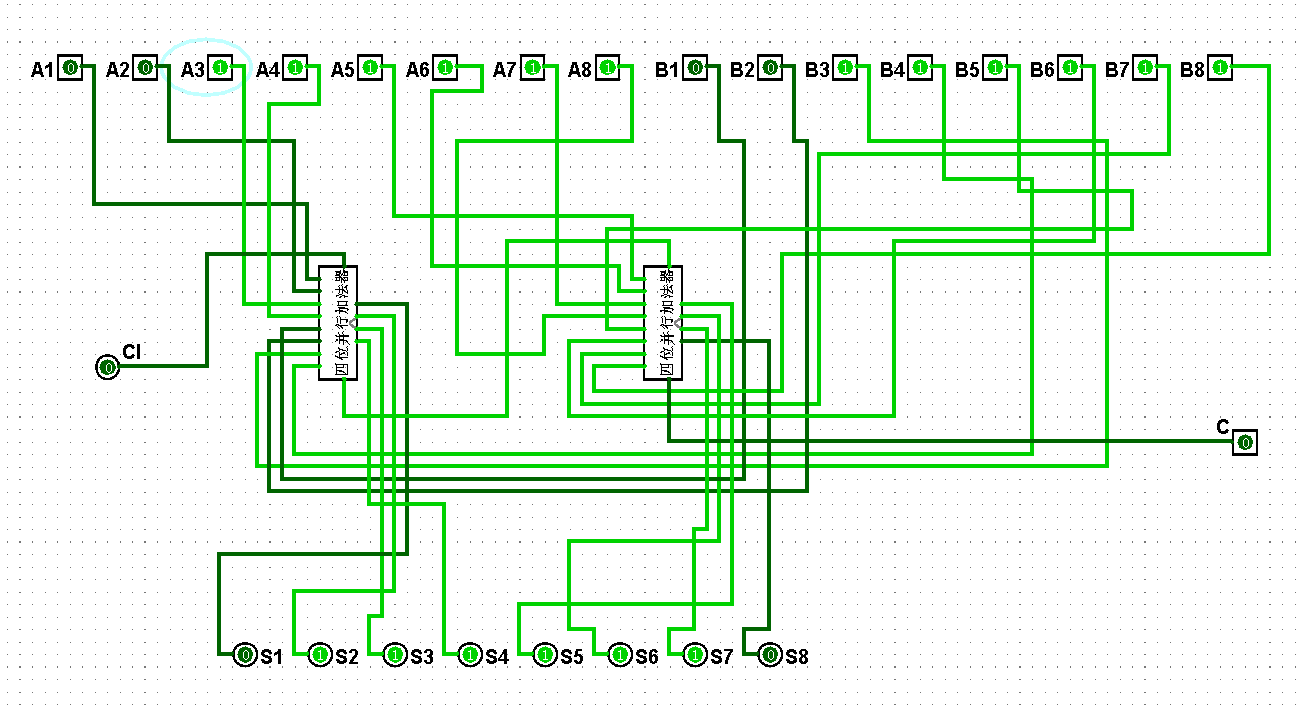
圖5-3-14 八位串行加法器測試63+63=126

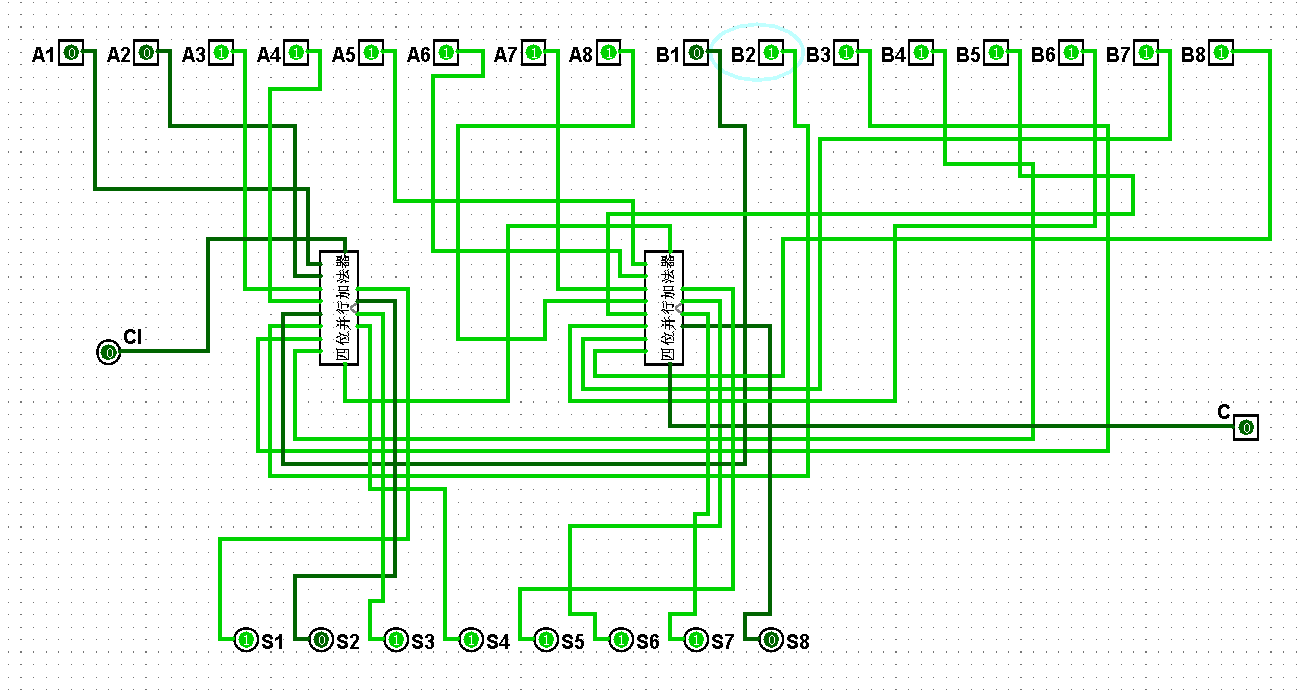
圖5-3-15 八位串行加法器測試63+127=190

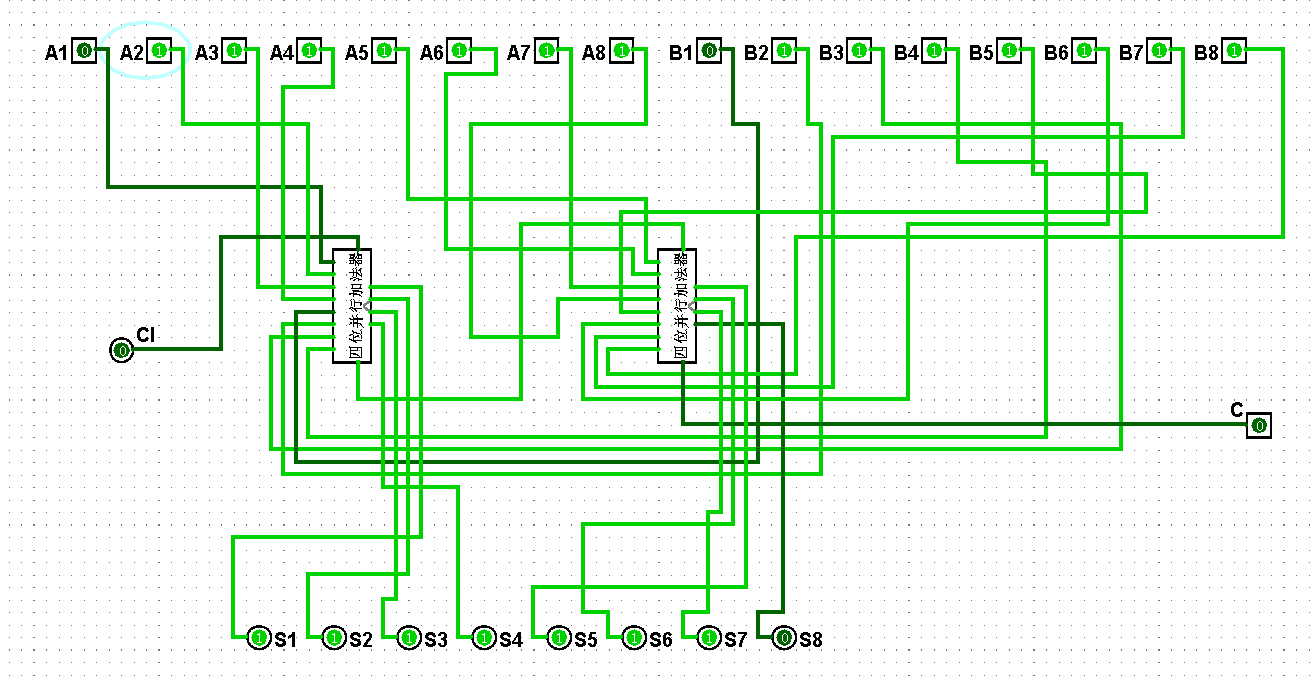
圖5-3-16 八位串行加法器測試127+127=254

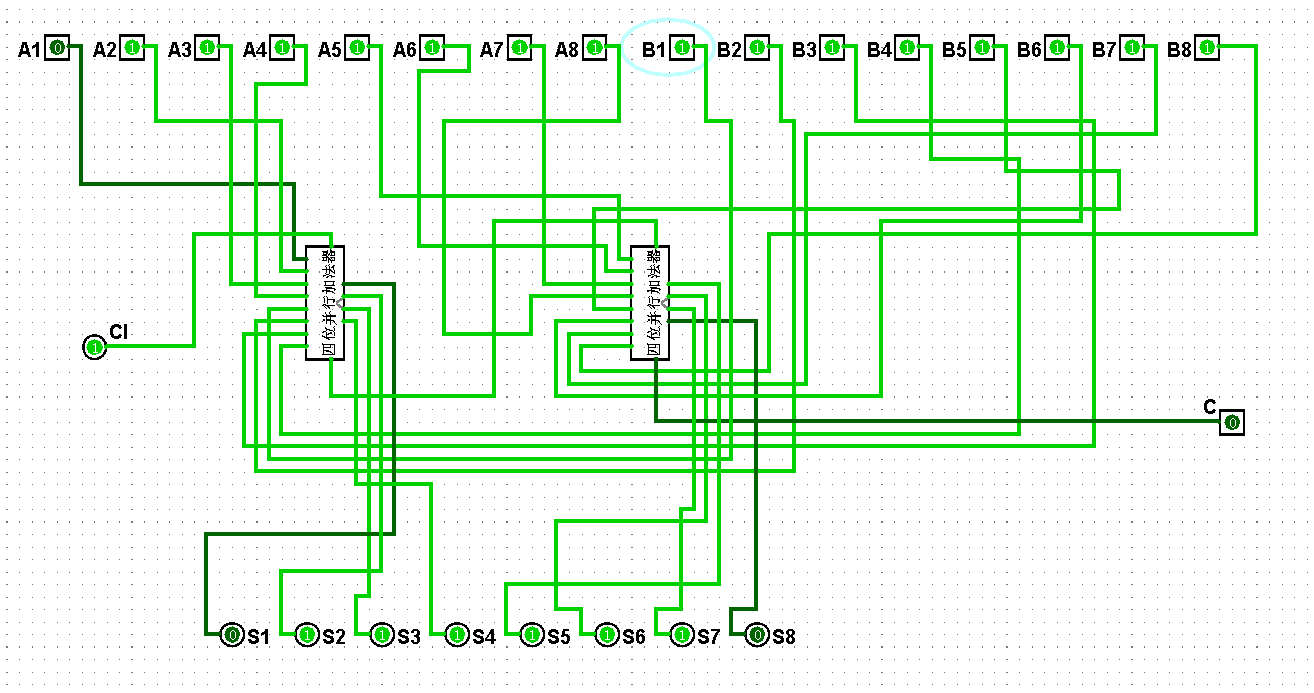
圖5-3-17 八位串行加法器測試127+255=382

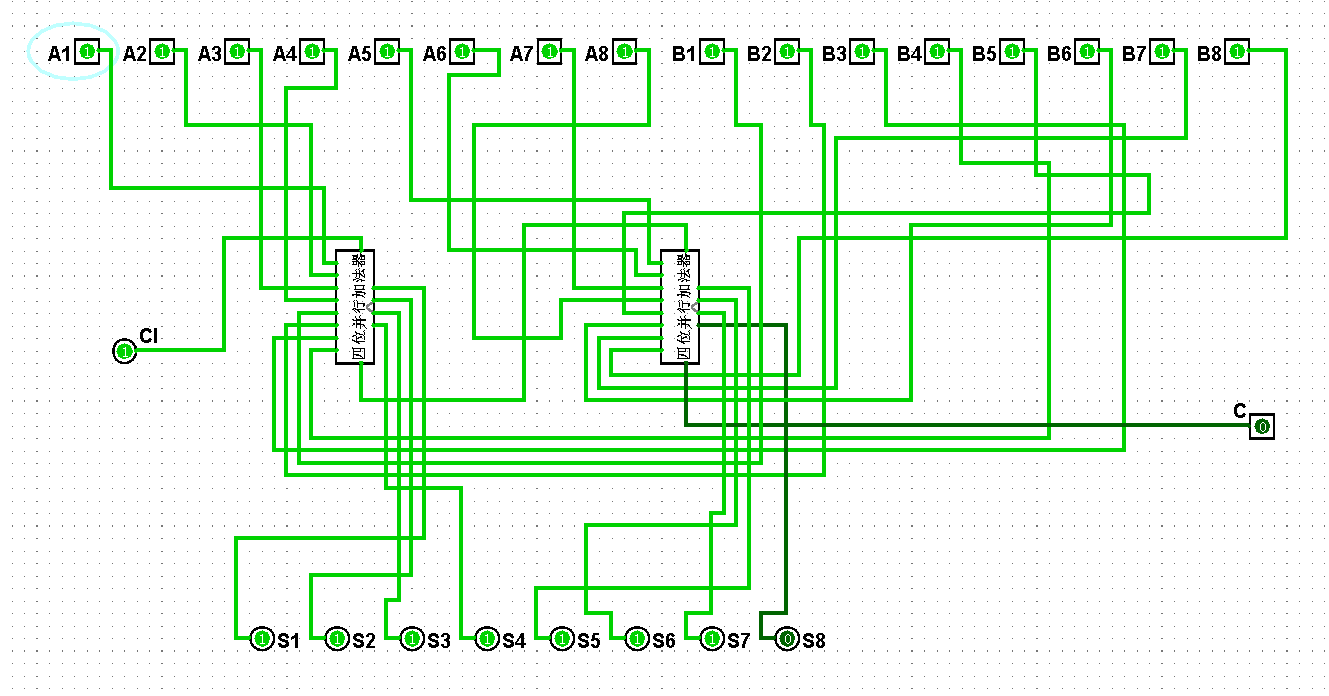
圖5-3-18 八位串行加法器測試255+255=510

4、打開Logisim軟件，利用兩個四位二進制加法器實現八位并行加法器，列出八位并行加法器邏輯電路真值表，并使用兩個四位二進制加法器實現八位并行加法器邏輯電路，鋪設完成后進行測試進而判斷電路是否鋪設成功。

????????（1）通過同時共享各位進位的方式搭建八位并行加法器，將低位的高位進位結果得到后進入高位的低位進位，進而使兩個四位二進制加法器同時處于工作狀態，實現八位并行加法器的邏輯電路，對應的部分八位并行加法器邏輯電路真值表如圖5-4-1所示：

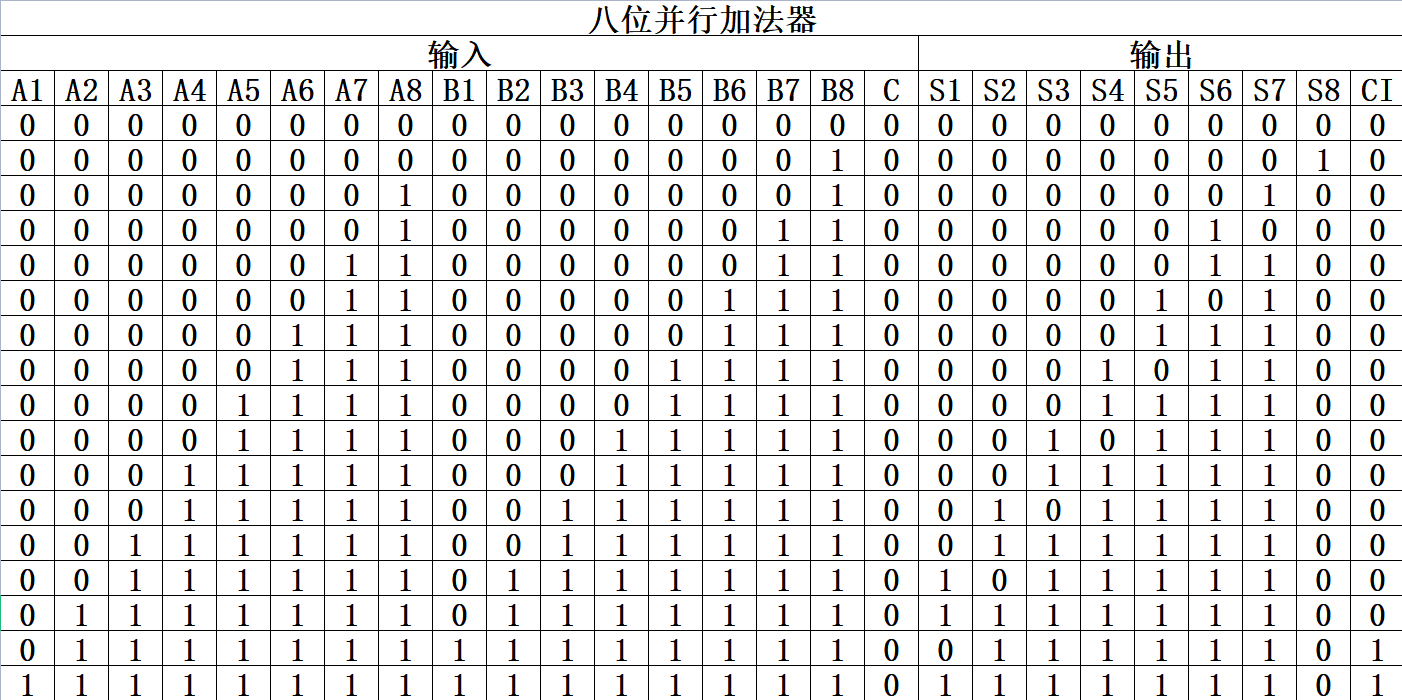
圖5-4-1 八位并行加法器邏輯電路真值表

????????（2）依據邏輯原理完成八位并行加法器邏輯電路的架構，在運行過程中將低位的高位進位結果共享到各個高位的低位進位上，將對應的進位進行構連即可實現八位并行加法器，對應的八位并行加法器邏輯電路如圖5-4-2至5-4-18所示：

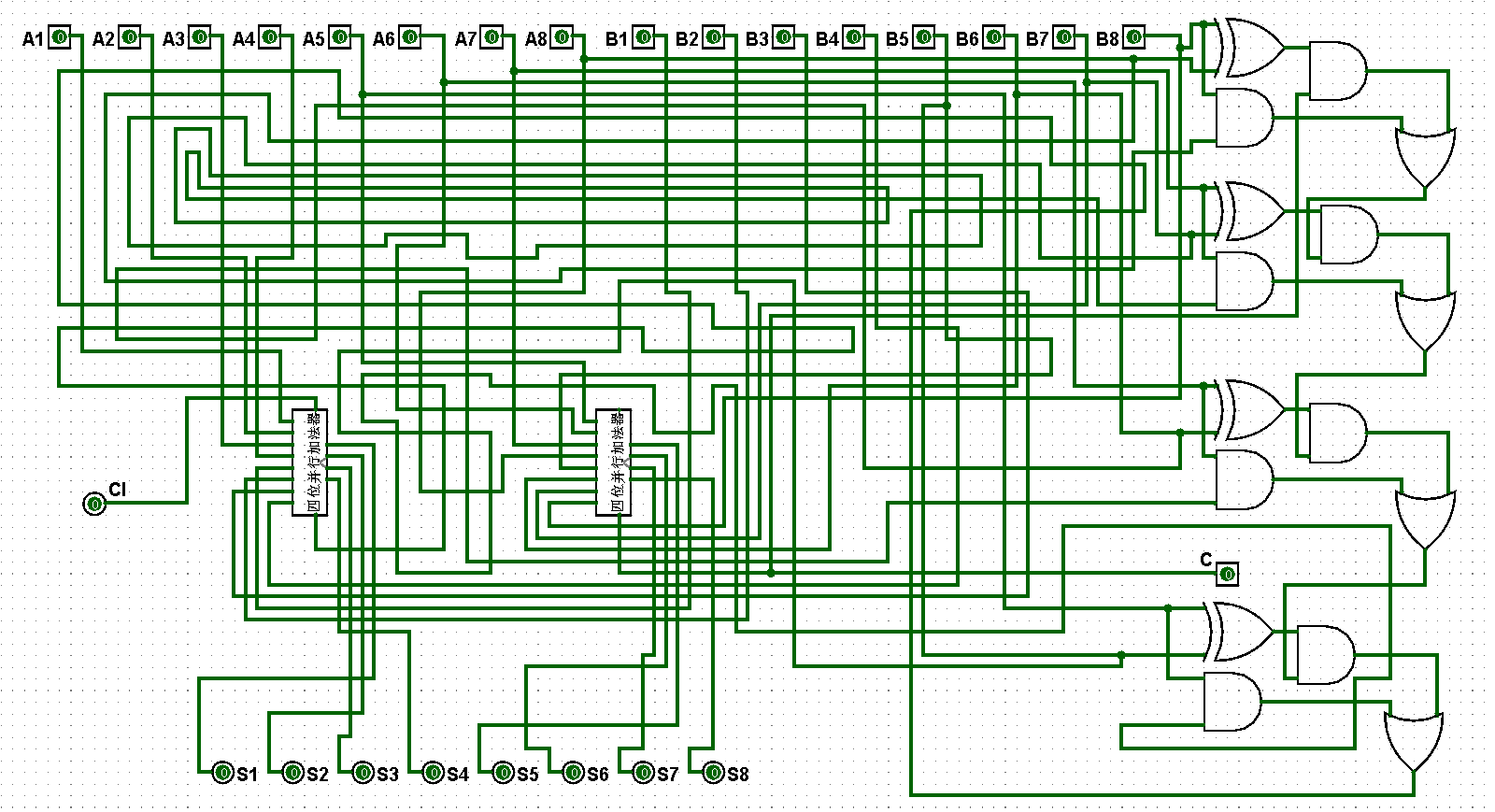
圖5-4-2 八位并行加法器邏輯電路

????????（3）八位并行加法器邏輯電路鋪設完畢后進行測試，進而判斷自己的電路是否鋪設成功，經過測試后此電路狀態一切正常，對應的八位并行加法器邏輯電路測試如圖5-4-3至5-4-18所示：

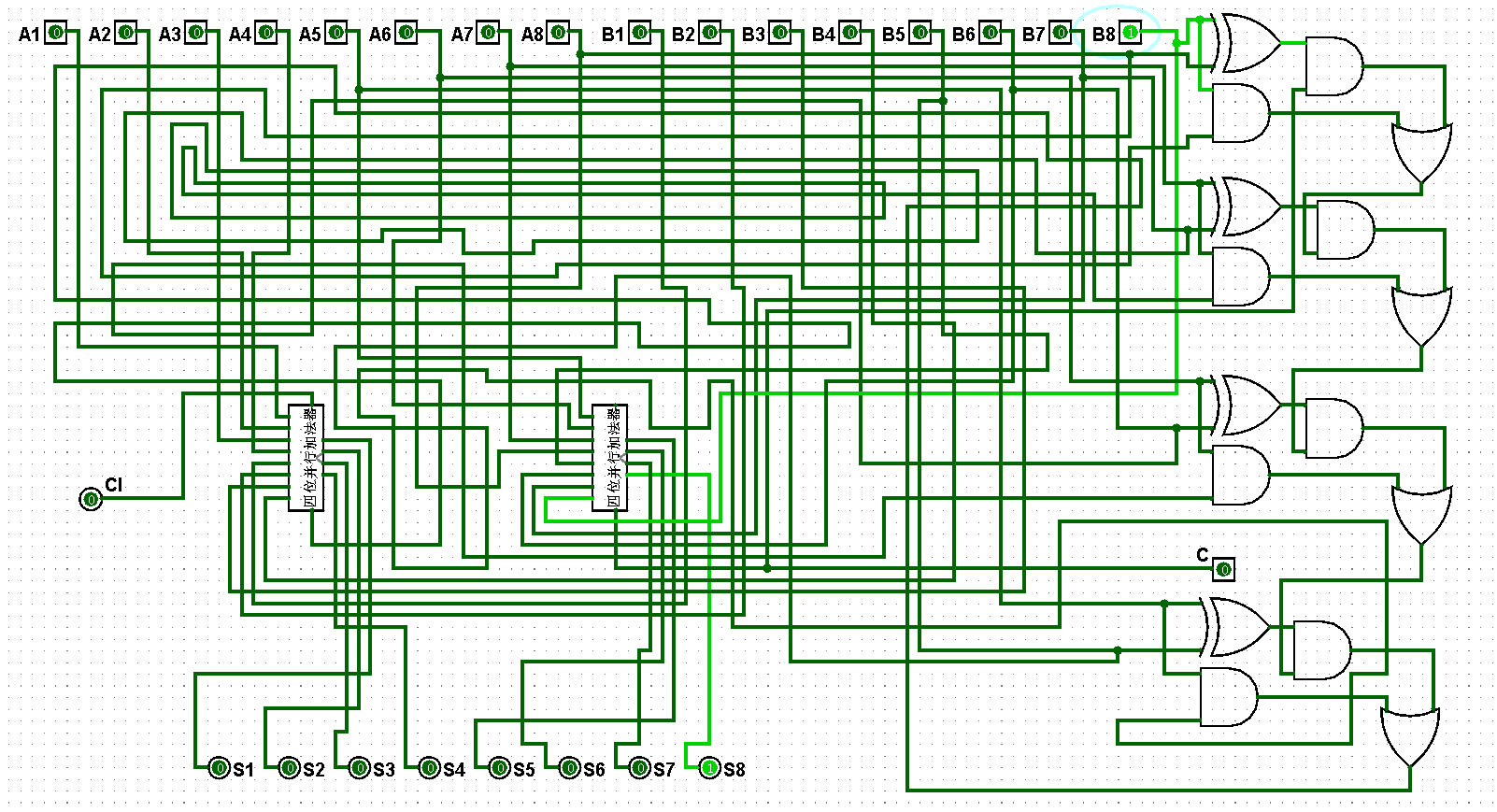
圖5-3-3 八位并行加法器測試0+1=1

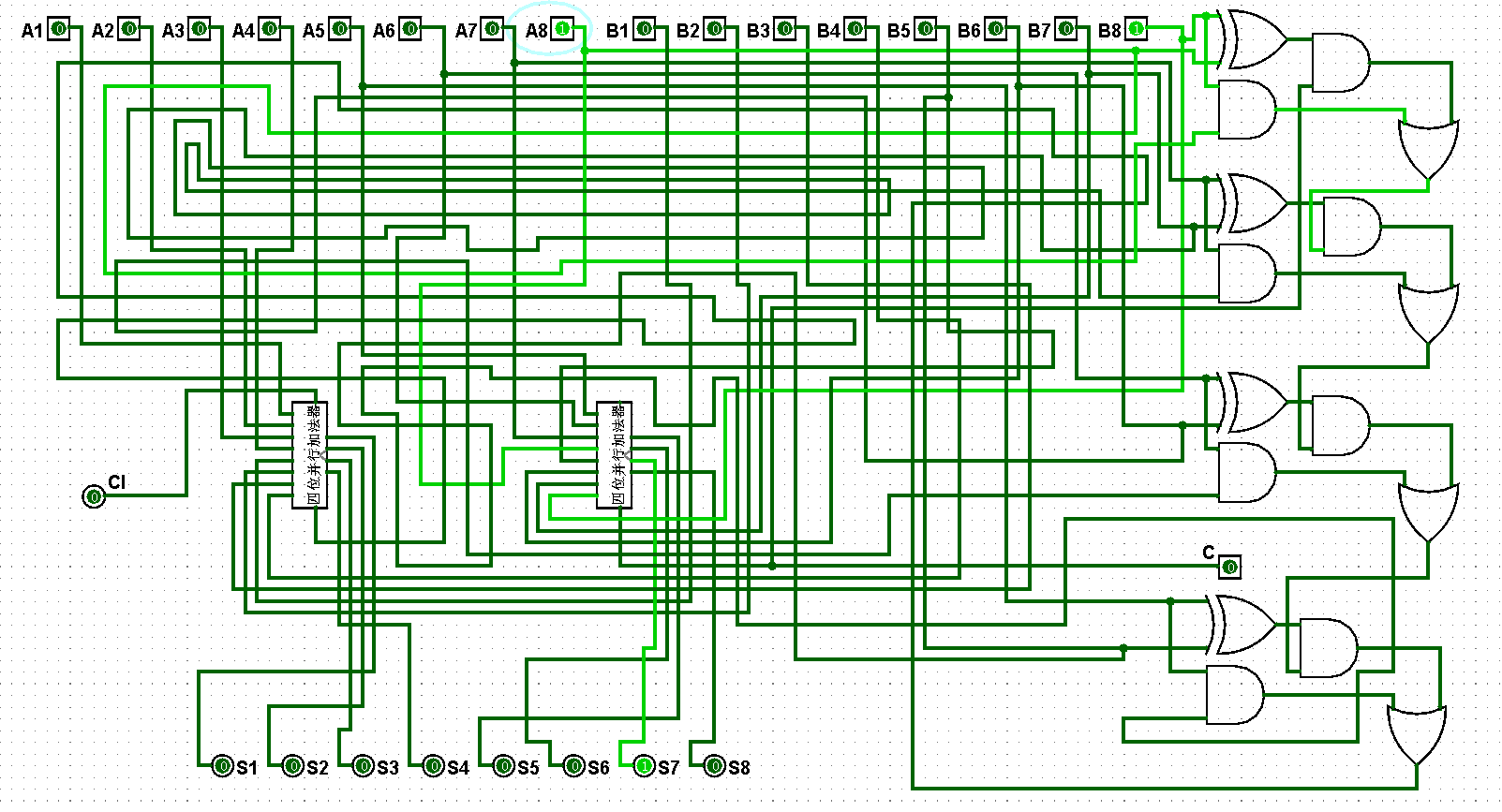
圖5-3-4 八位并行加法器測試1+1=2

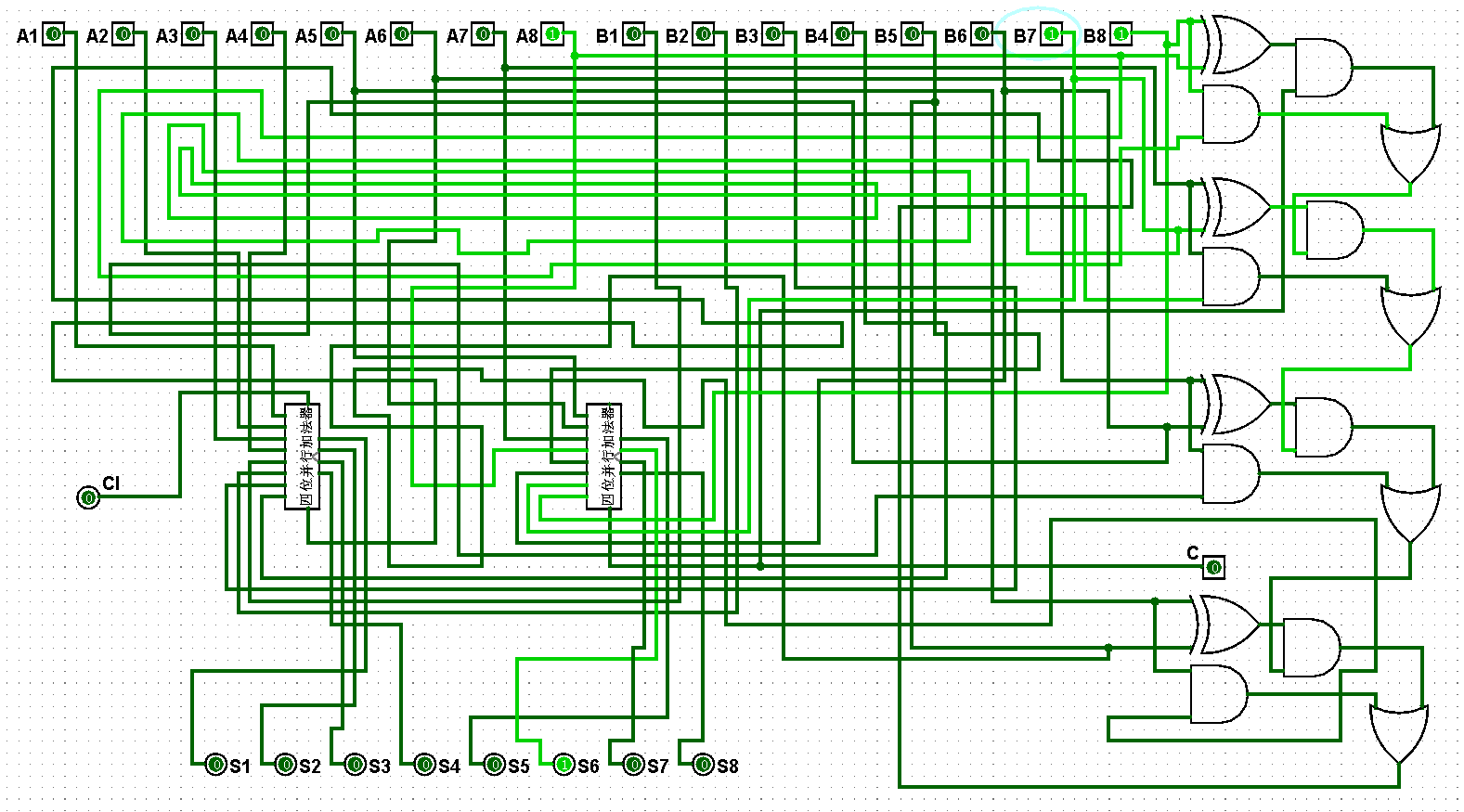
圖5-3-5 八位并行加法器測試1+3=4

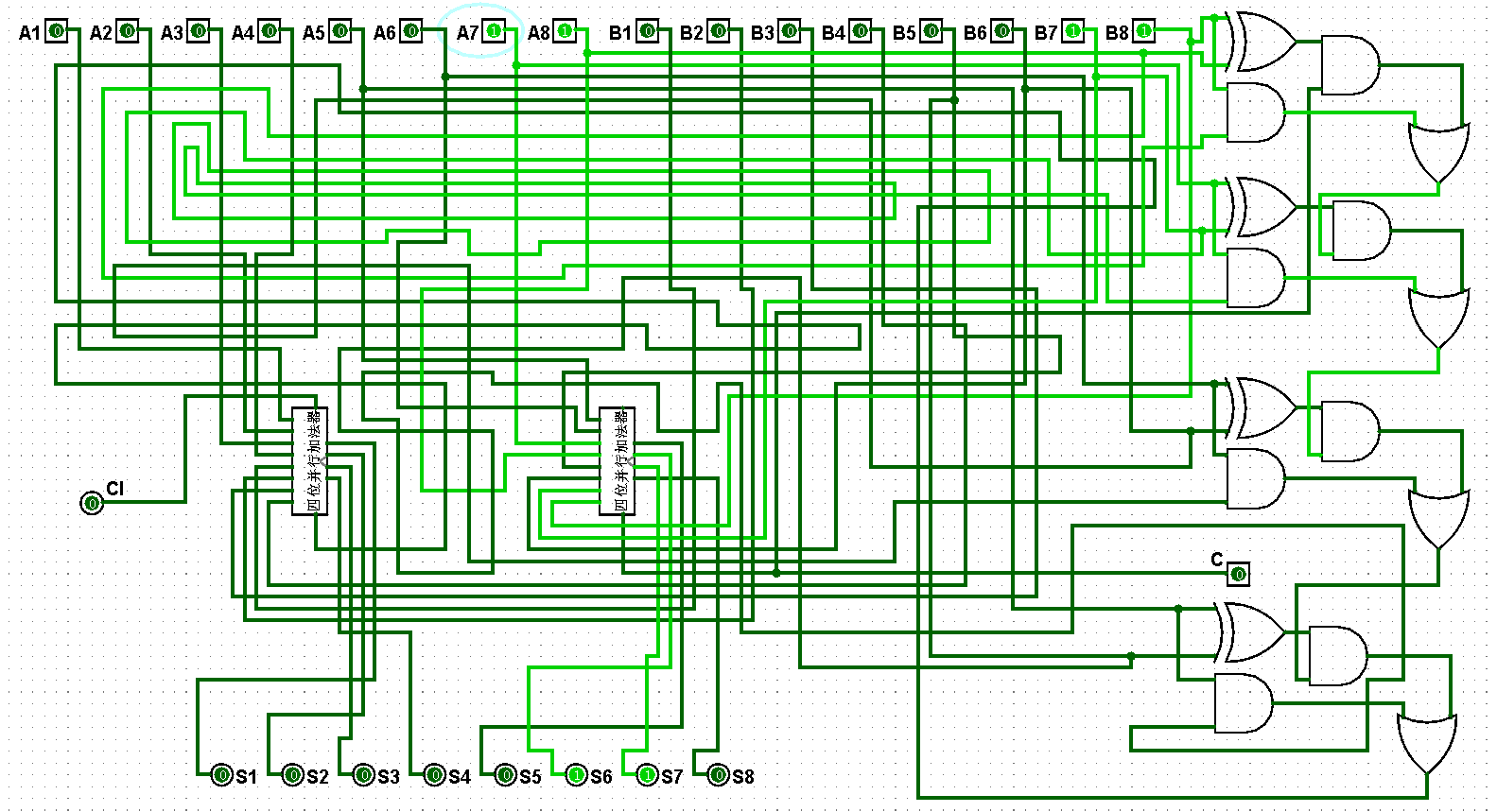
圖5-3-6 八位并行加法器測試3+3=6

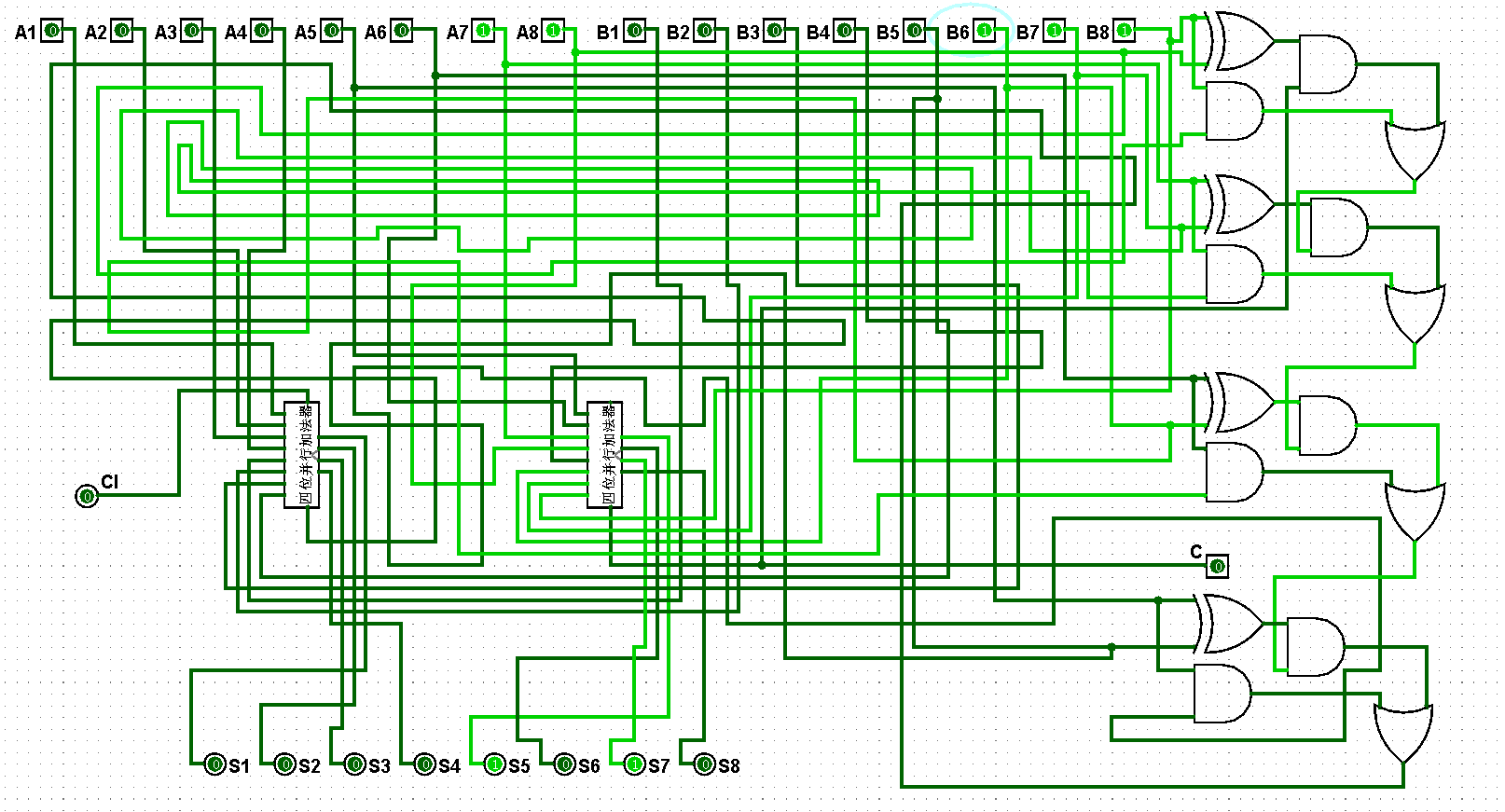
圖5-3-7 八位并行加法器測試3+7=10

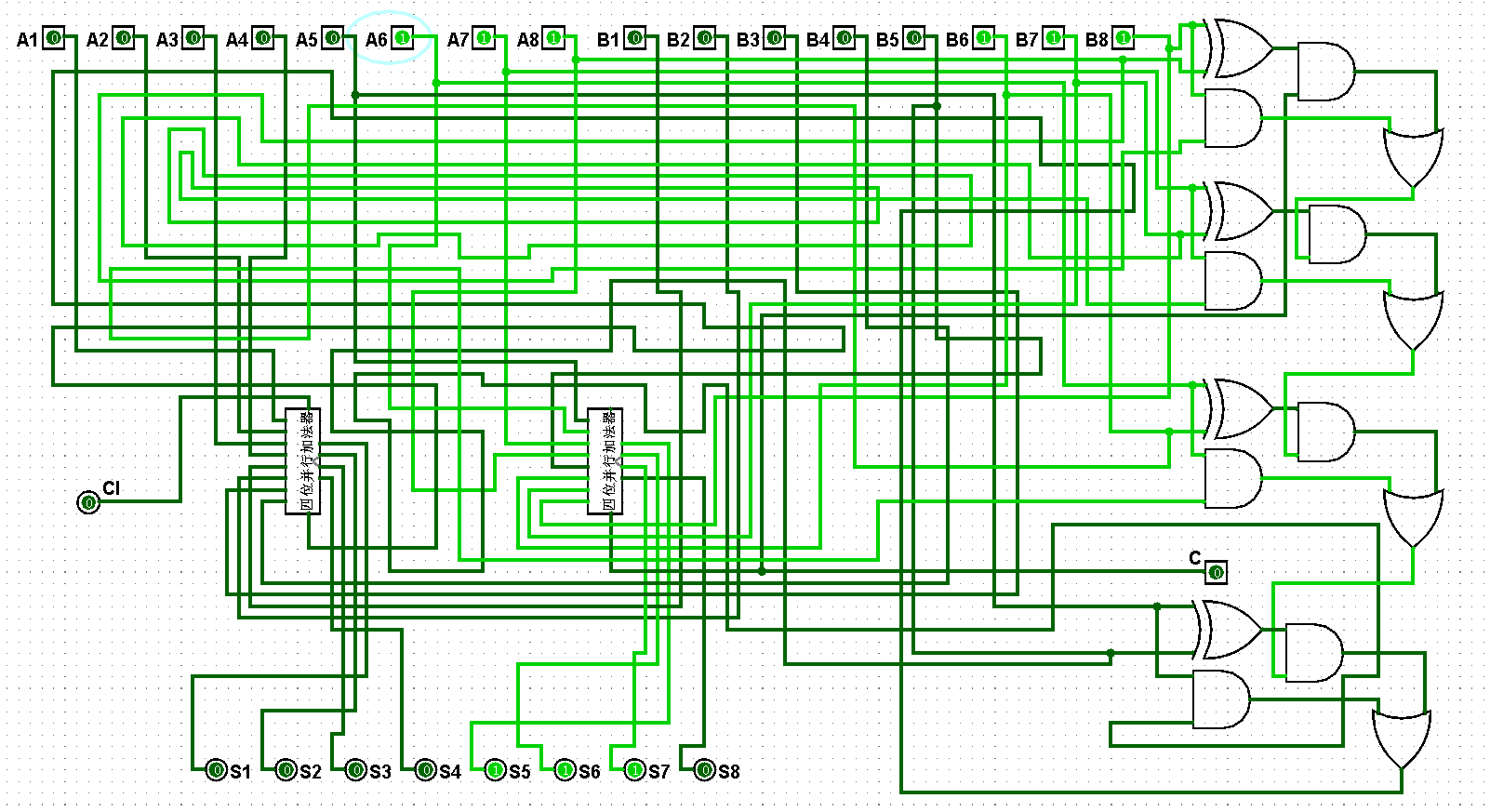
圖5-3-8 八位并行加法器測試7+7=14

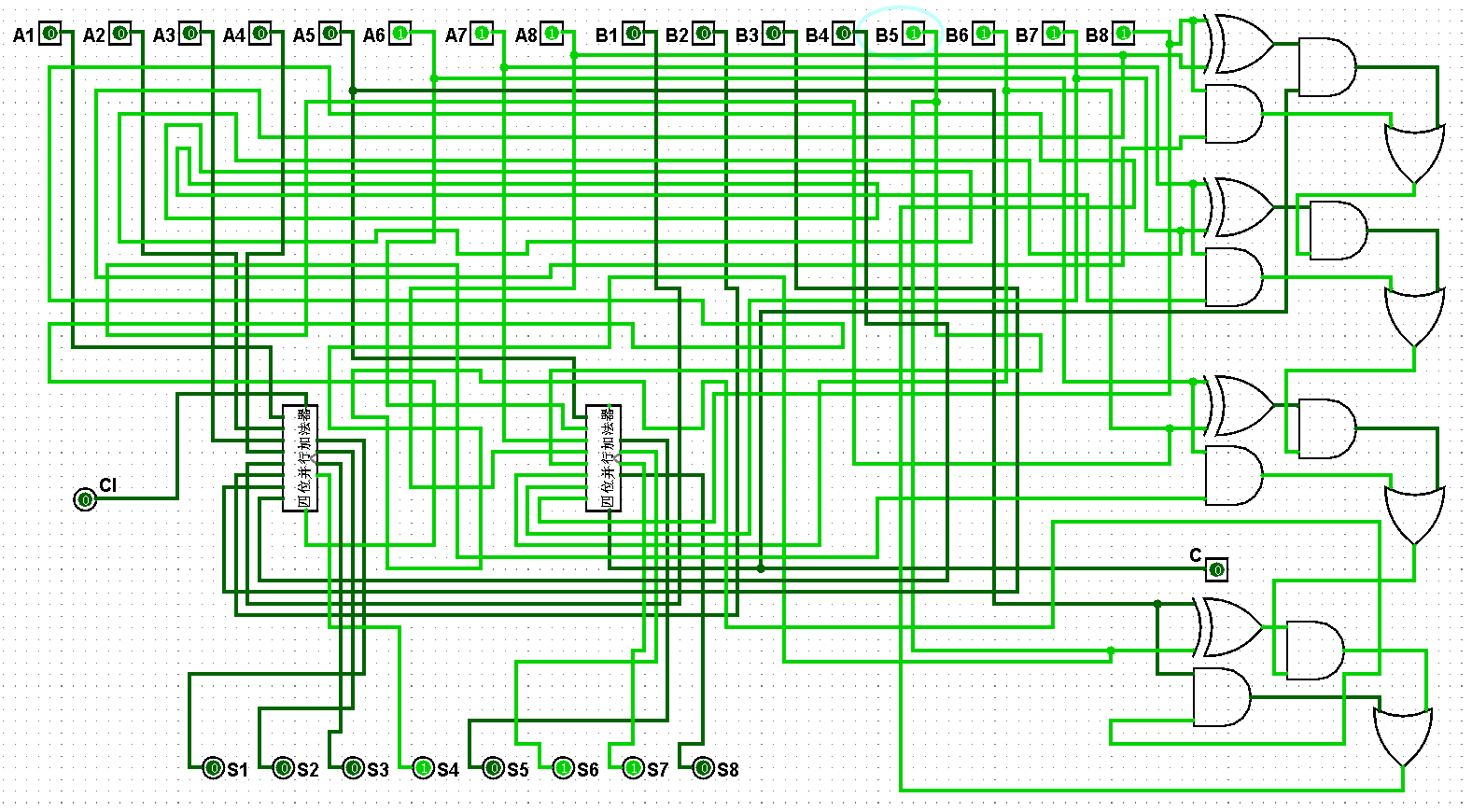
圖5-3-9 八位并行加法器測試7+15=22

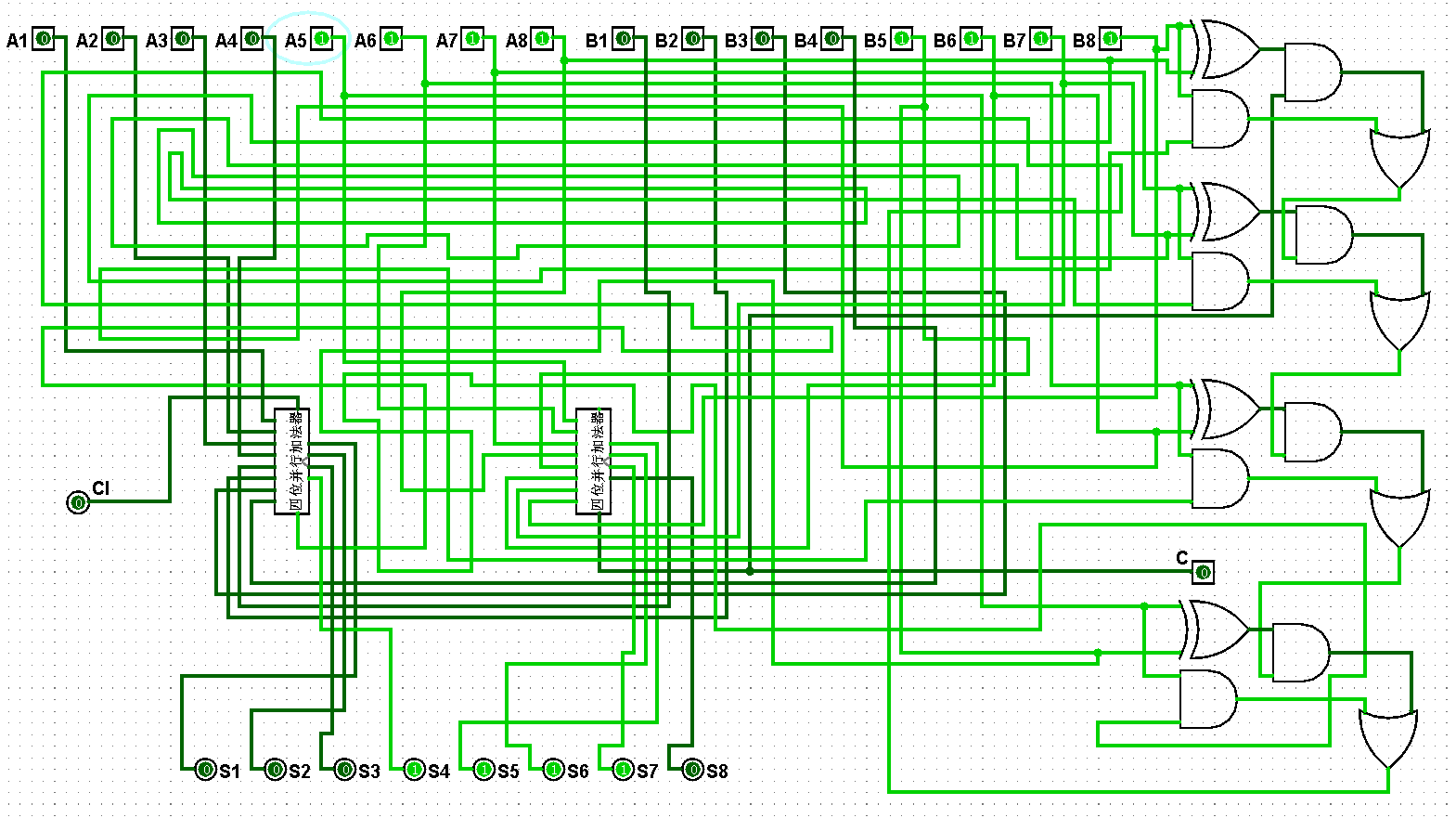
圖5-3-10 八位并行加法器測試15+15=30

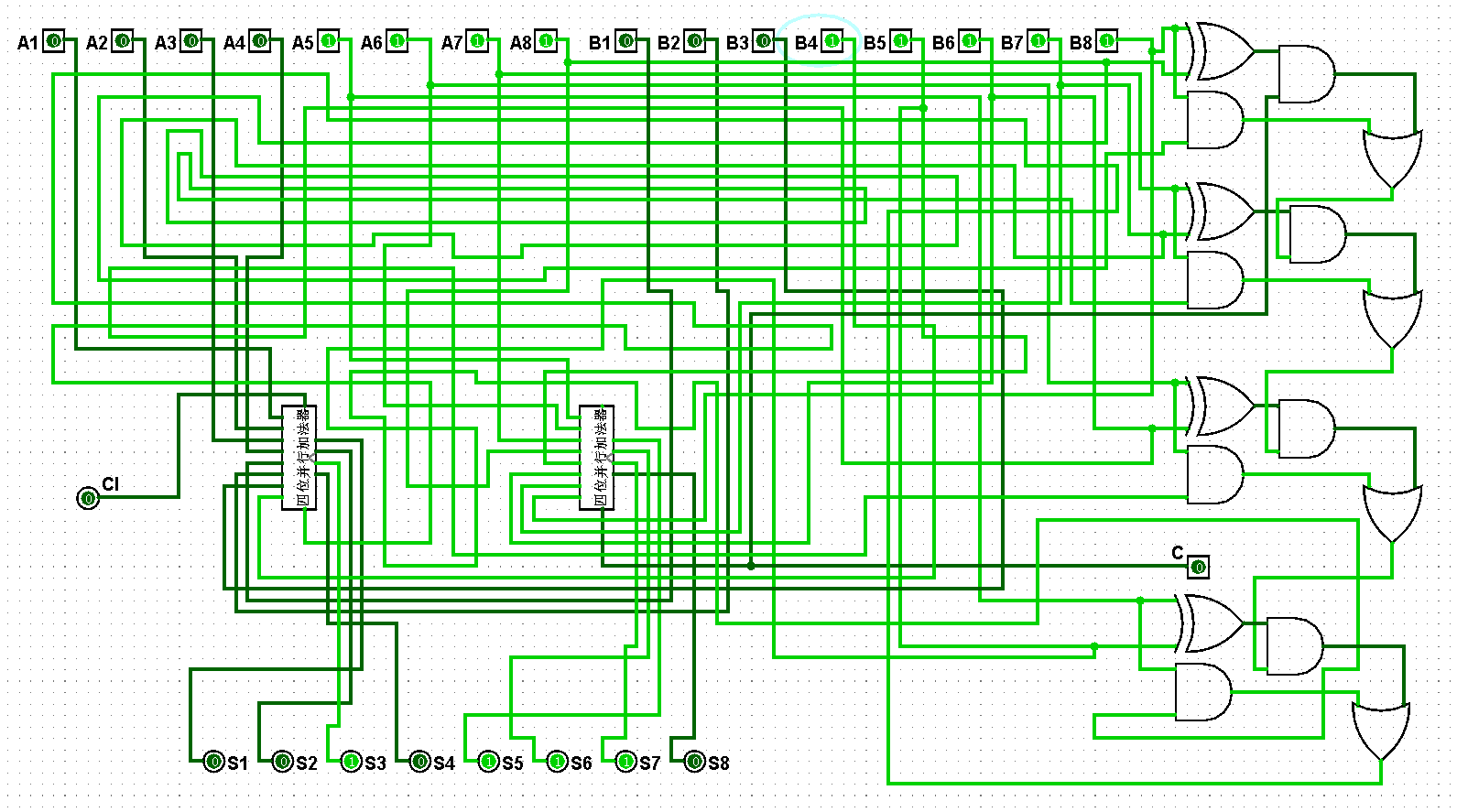
圖5-3-11 八位并行加法器測試15+31=46

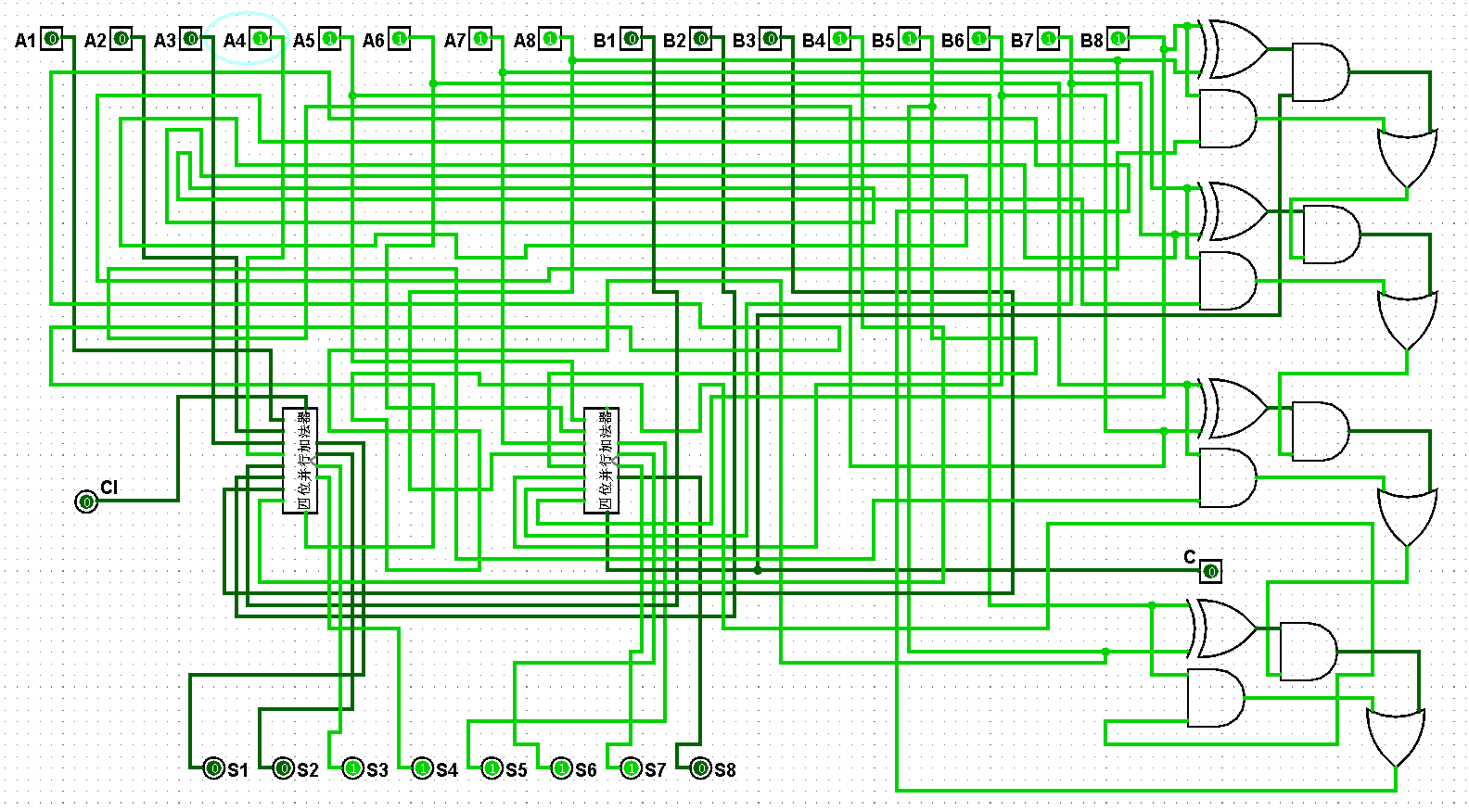
圖5-3-12 八位并行加法器測試31+31=62

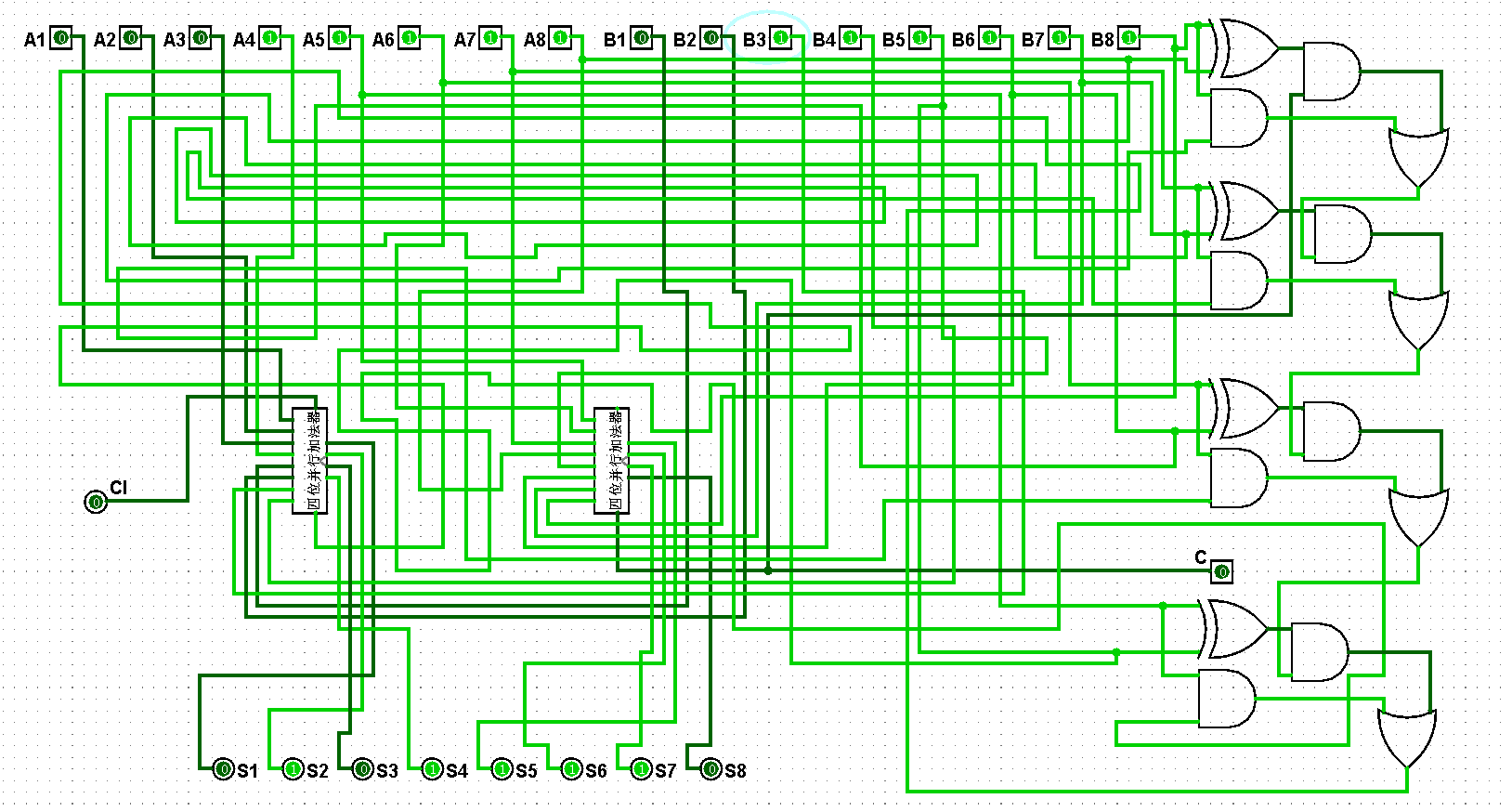
圖5-3-13 八位并行加法器測試31+63=94

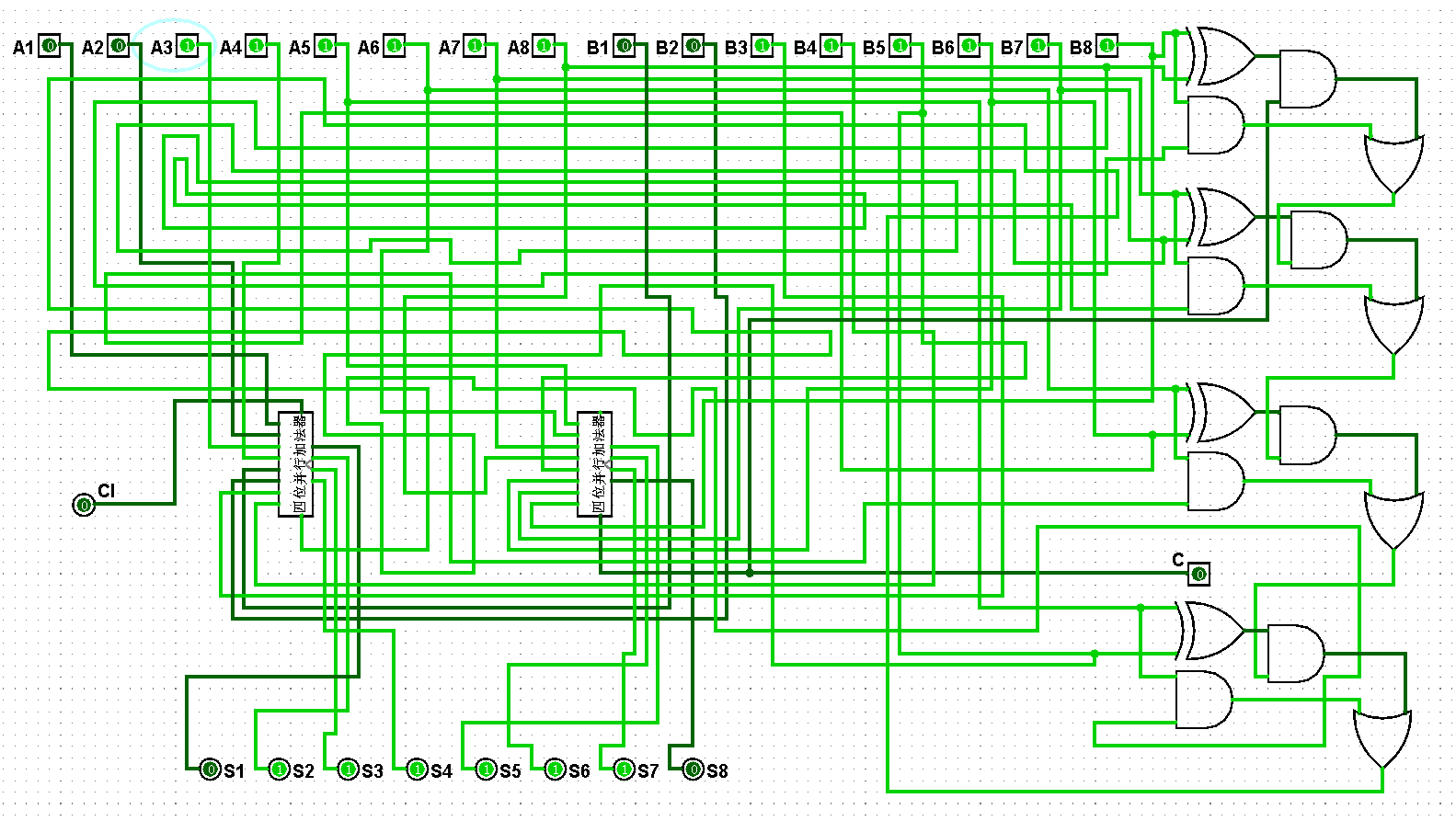
圖5-3-14 八位并行加法器測試63+63=126

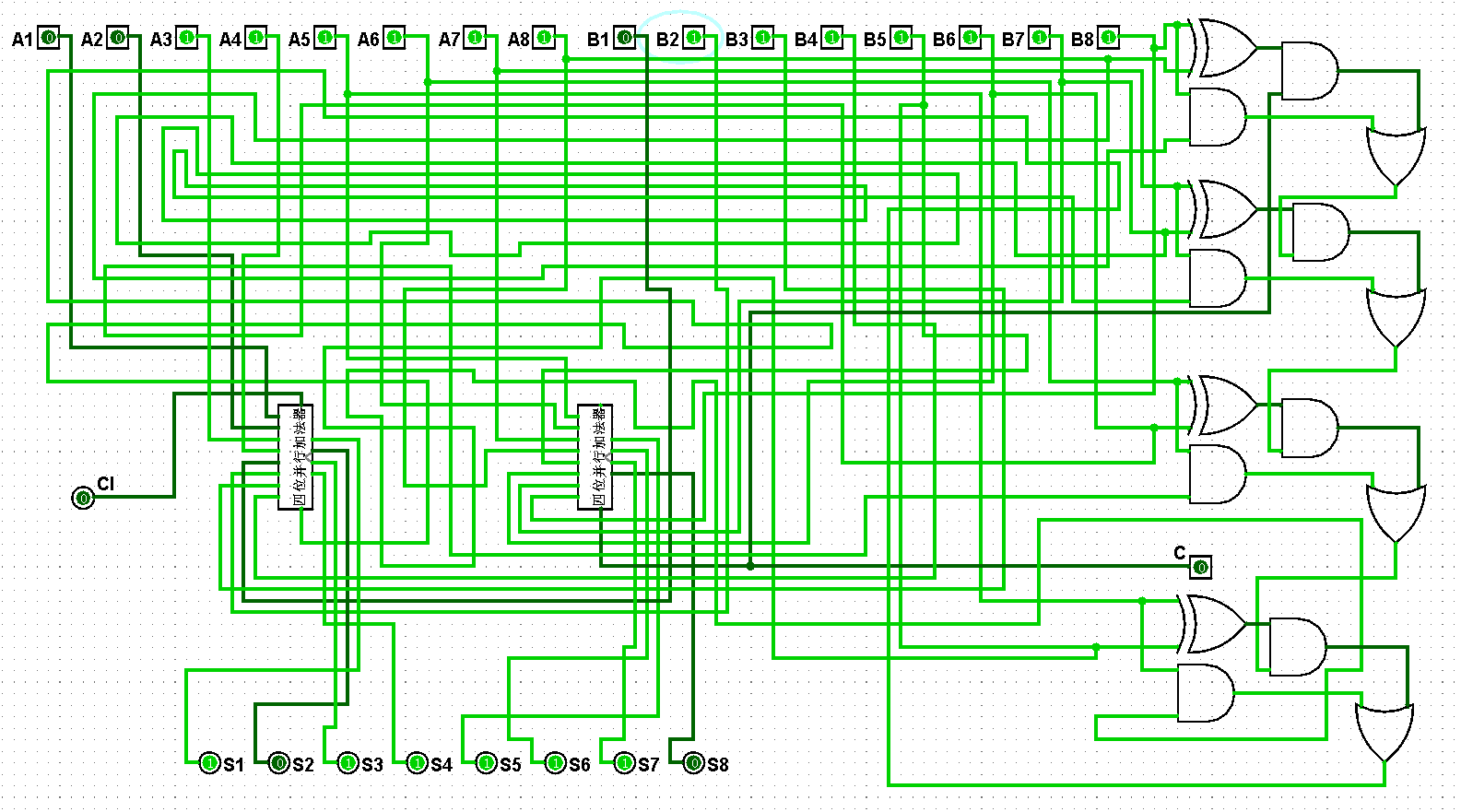
圖5-3-15 八位并行加法器測試63+127=190

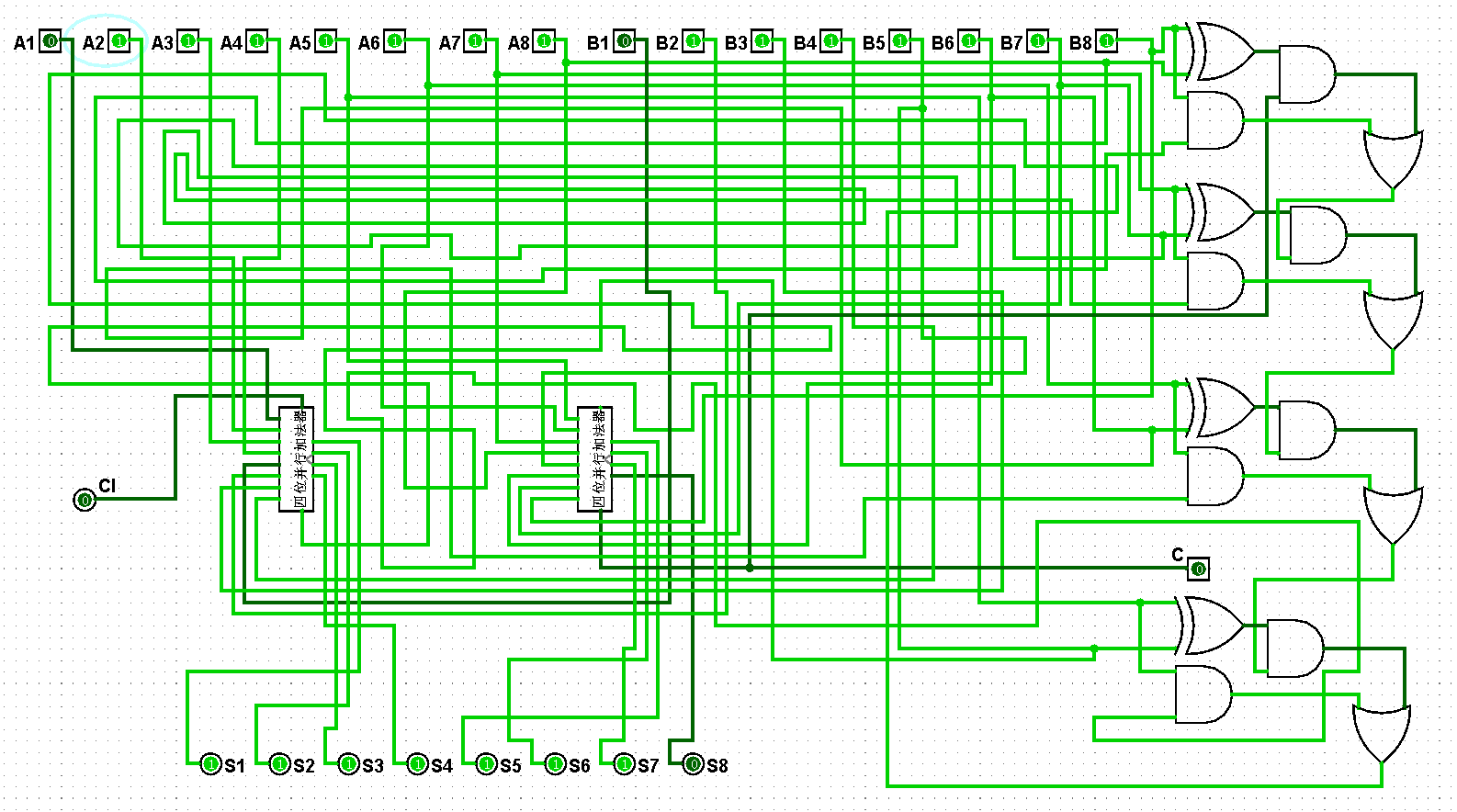
圖5-3-16 八位并行加法器測試127+127=254

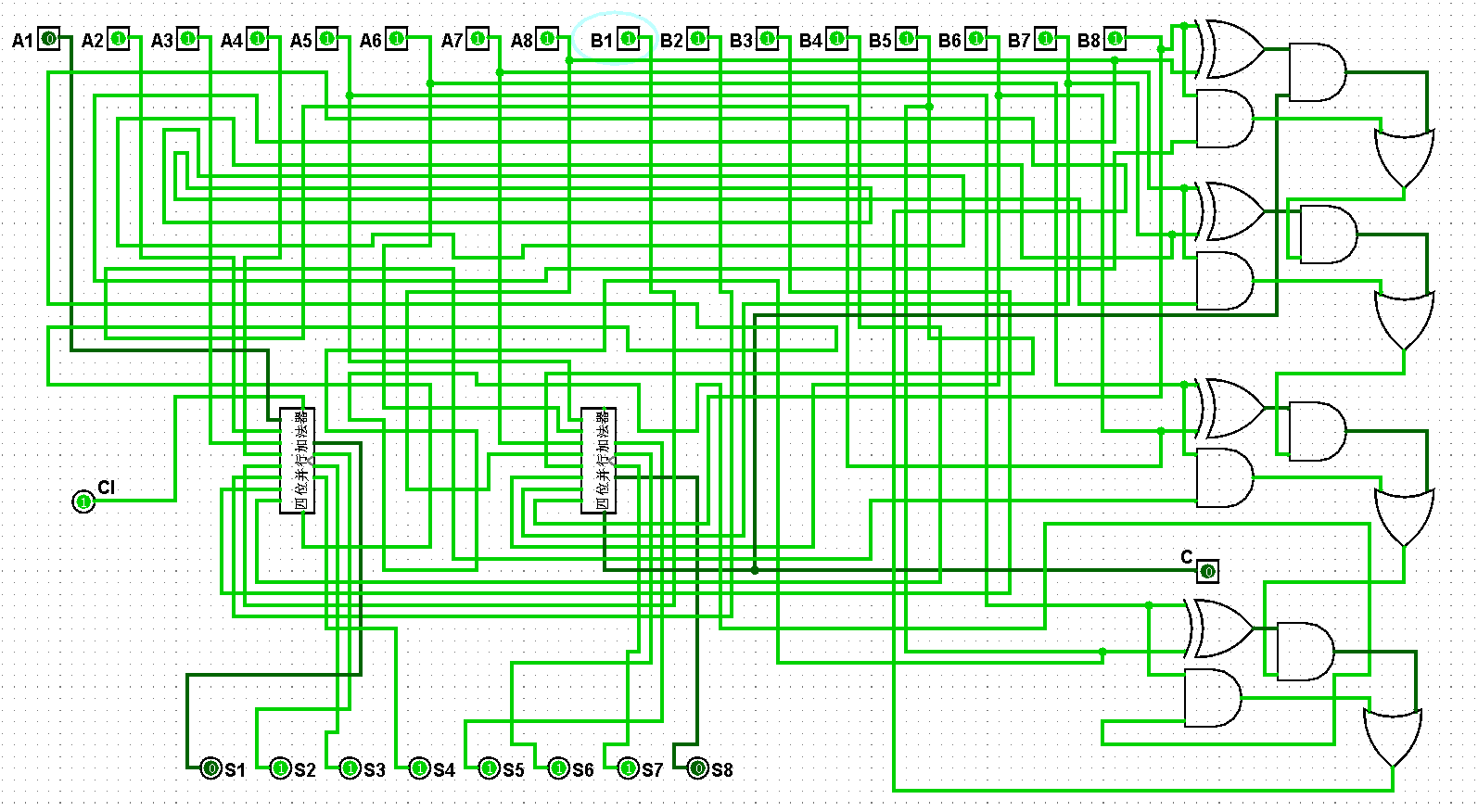
圖5-3-17 八位并行加法器測試127+255=382

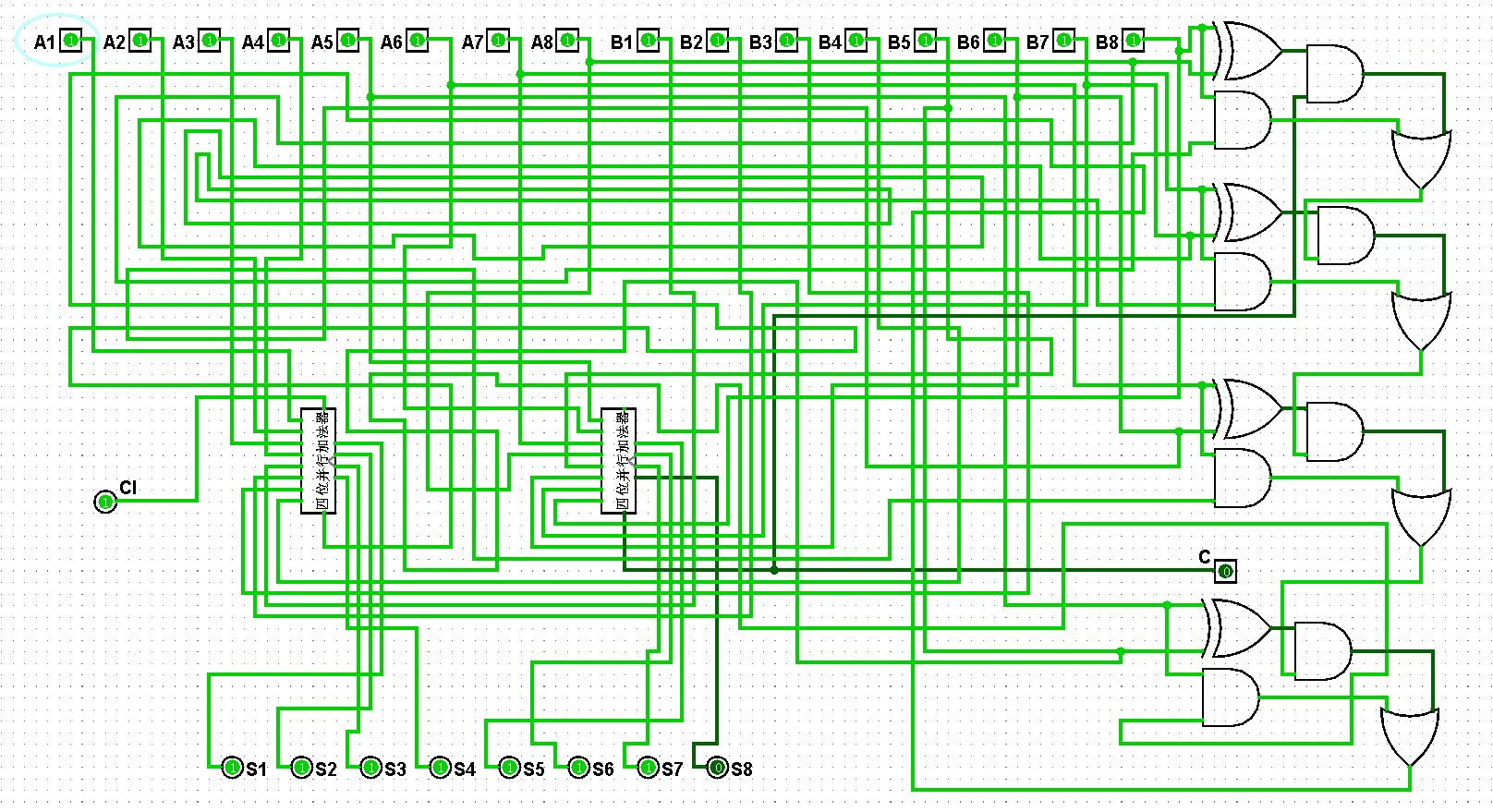
圖5-3-18 八位并行加法器測試255+255=510

5、打開Logisim軟件，用自己學號（20212501238）最后兩位數字（38）轉化為二進制（00000011，00001000）作為輸入，測試兩個八位加法器的功能。

????????（1）將對應的八位二進制分別輸入到八位串行加法器和八位并行加法器中進行運算，對應的八位串行加法器、八位并行加法器邏輯電路真值表分別如圖5-5-1、5-5-2所示：

圖5-5-1 八位串行加法器邏輯電路真值表

圖5-5-2 八位并行加法器邏輯電路真值表

????????（2）將轉化后的八位二進制直接輸入到對應的加法器中進行計算輸出即可，對應的八位串行加法器、八位并行加法器輸入邏輯電路分別如圖5-5-3、5-5-4所示：

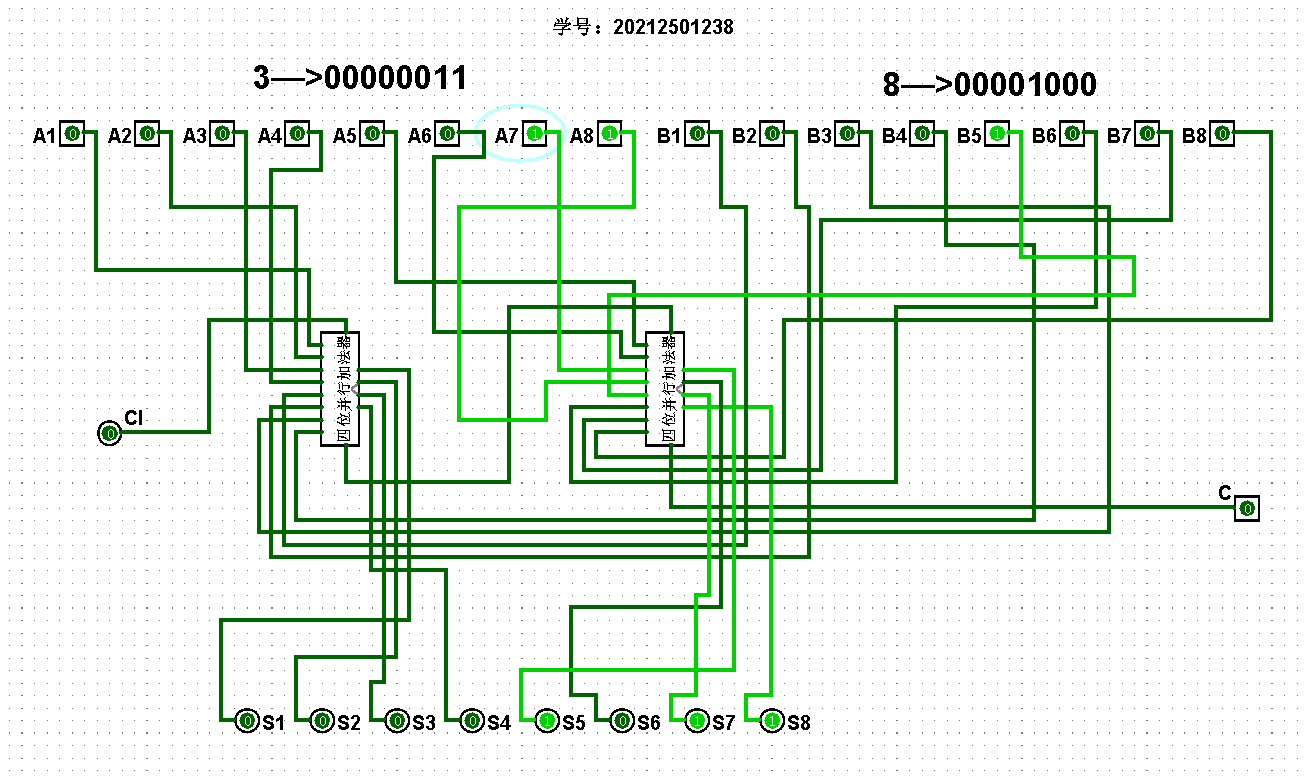
圖5-5-3 八位串行加法器輸入邏輯電路

圖5-5-4 八位并行加法器輸入邏輯電路

六、實驗小結

1、問題和解決方法：

????????（1）實驗問題：使用邏輯門和相關元素構建邏輯電路后發現有時輸出結果與自己的真值表內容不符。

解決方法：觀察自己的邏輯電路后發現部分邏輯門的引腳過多，與、或、非等邏輯門的默認引腳的個數為5個，因此我們需要根據自己需要的引腳數量進行設置，將對應的引腳數量改為自己需要的2個引腳后對應問題得到解決。

????????（2）實驗問題：在對邏輯門進行連線的過程中發現電路中出現了多余的連線。

解決方法：點擊對應多余的連線并進行刪除操作或者對該條連線重新進行勾連。

????????（3）實驗問題：邏輯電路連接完成后發現部分輸入端或者輸出端是藍色，且點擊輸入端進行數值切換對藍色的輸出端無影響。

解決方法：線路沒有徹底連接，輸入端和輸出端的引腳默認朝西，所以在連接電路時要首先將對應端口的引腳方向進行設置，進而方便邏輯電路的正常連接。

????????（4）實驗問題：邏輯電路中有部分區域的連線為紅色。

解決方法：由于紅色連線前方處于斷路狀態，邏輯信號無法正常到達后續的邏輯電路之中，因此出現了紅色連線，將對應區段的電路連接通路后即可恢復正常。

????????（5）實驗問題：在使用兩個以上的異或門進行邏輯電路操作時發現出現了錯誤。

解決方法：由于Logisim允許指定異或門的邏輯行為，默認是當一個輸入為1是輸出為1，另一種是奇數個1輸入時輸出為1，因此在使用過程中需要對默認值進行相應的修改操作，進而避免錯誤的出現。

????????（6）實驗問題：邏輯電路設計完畢以后，出現了紅色或者橘紅色的線條，但是自己的邏輯電路沒有任何的錯誤。

解決方法：由于軟件本身因素引起的，因此對自己的邏輯電路進行保存，關閉Logisim軟件后重新打開對應的邏輯電路文件后即可恢復正常。

2、心得體會：

????????（1）通過使用Logisim軟件對邏輯電路進行操作，讓我熟悉了相關的邏輯符號及邏輯運算等。其中藍色的方框表示輸入信號；藍色的圓框表示輸出信號；綠色的圓圈加上短橫表示錨，主要用于移動和定位。

????????（2）邏輯電路是用來對數字信號進行邏輯運算，以實現邏輯命題的電路。

????????（3）組合邏輯電路中電路的輸出只與該時刻的輸入有關，而時序邏輯電路中電路的輸出不僅與該時刻的輸入有關，還與電路的原狀態有關。

????????（4）真值表是描述邏輯功能的最底層工具，它是先結構而后內容的，列數據時輸入部分從全0到全1，逐個遞增。

????????（5）基本邏輯運算是與、或、非，而常用的復合邏輯為與非、或非、與或非、異或、同或。

????????（6）邏輯門電路（門電路）用于實現各種的基本邏輯運算、常用符合邏輯運算的電子電路。

????????（7）兩輸入異或、同或互為反函數，即非關系。

????????（8）兩輸入異或、同或的功能為：

????????兩輸入異或，輸入取值不同，輸出1，輸入取值相同，輸出0；

????????兩輸入同或，輸入取值不同，輸出1，輸入取值相同，輸出0.

? ? ? ? （9）n輸入異或的功能為當輸入中有奇數個1時，輸出值為1，有偶數個1時輸出值為0.

? ? ? ? （10）n為偶數時，異或、同或互為非關系；n為奇數時，異或、同或功能相同。

? ? ? ? （11）編碼器用于編碼，使用二進制代碼表示具有某種特定含義的信號，即輸入信號輸出代碼。

? ? ? ? （12）譯碼器用于譯碼，將使用一組代碼表示的特定含義翻譯出來，即輸入代碼輸出信號。

? ? ? ? （13）進行溢出判斷時可以采取以下三種方法進行判斷：

????????①用計算結果的符號位來判斷溢出。

????????②用計算結果最高數值位向符號位的進位值c1與符號位的進位值c0來判斷溢出。

????????③采用雙符號位進行判斷。

? ? ? ? （14）多位加法器的構成有兩種方式:并行進位和串行進位方式。

? ? ? ? （15）并行進位加法器設有并行進位產生邏輯，運算速度快;串行進位方式是將全加器級聯構成多位加法器。

? ? ? ? （16）通常，并行加法器比串行級聯加法器占用更多的資源，并且隨著位數的增加，相同位數的并行加法器比串行加法器的資源占用差距也會越來越大。

? ? ? ? （17）多位全加器連接可以是逐位進位，也可以是超前進位。逐位進位也稱串行進位，其邏輯電路簡單，但速度也較低。