目錄
?1、聚類任務
2、性能度量
(1)外部指標
(2)內部指標
?3、具體聚類方法
(1)原型聚類
(2)密度聚類
(3)層次聚類
“無監督學習”(unsupervised learning):訓練樣本的標記信息是未知的,目標是通過對無標記訓練樣本的學習來揭示數據的內在性質及規律,為進一步的數據分析提供基礎。“聚類”(clustering)是無監督任務中研究最多,應用最廣
聚類:試圖將數據集中的樣本劃分為若干個通常是不相交的子集聚類既能作為一個單獨過程,用于找尋數據內在的分布結構,也可作為分類等其他學習任務的前驅過程。它本著的是物以類聚,人以群居的這個方式來進行的,它并不需要標簽,但是它能夠把相似的樣本聚成一類
?
?1、聚類任務


2、性能度量
????????原來的時候是帶有標簽的,預測結果和標簽結果進一個比較。這樣的話我就知道我這個聚類到底是分對了還是我分類器是分對了分錯了,但是聚類任務中它是沒有標簽的話我怎么去度量我們這個分類的結果好壞?性能度量主要有兩個,一個是外部指標,一個是內部指標
(1)外部指標
? ? ? ? ? 外部指標是指的是我們在進行對具體方法的好壞進行評價的時候,我們要找一個參考模型。

有 了a,b,c,d這些值,就可以計算:

越大越好
(2)內部指標
????????不參考任何模型,只根據聚類結果進行判斷:類內相似度越高越好,類間相似度越差越好。簇內緊湊,簇間分散”

?輪廓系數

 ?
?
DB指數?

?距離計算:
????????如果這個屬性中它是離散的,而且它的屬性定義為飛機,火車和輪船。那么,我們怎么去計算飛機和火車之間的距離,怎么去計算火車和輪船之間的距離?通過分布形式比例的形式計算:
?3、具體聚類方法
(1)原型聚類
k-means算法 ※

學習向量量化算法:結合監督信息,通過原型向量(可理解為 “代表性樣本”)學習樣本的類別劃分,適用于帶有標簽的訓練數據。用監督信息輔助優化 “原型簇” 的劃分,核心邏輯仍是通過相似度分組(聚類的本質),因此屬于結合監督信號的聚類算法,監督信息是優化手段,而非改變其聚類的本質屬性。
高斯混合聚類

(2)密度聚類
DBSCAN
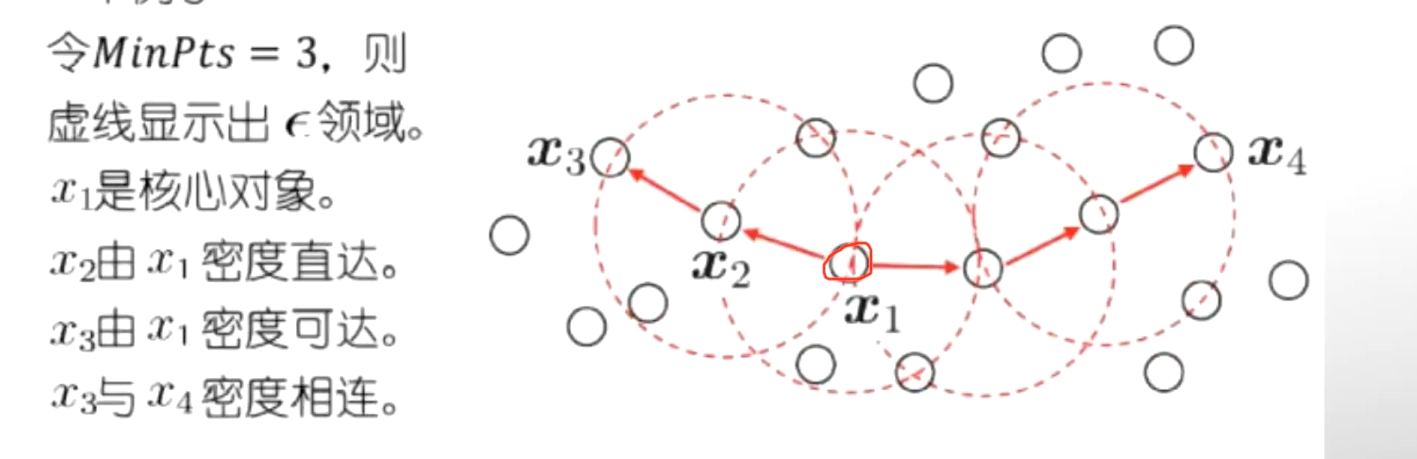

(3)層次聚類
????????層次聚類通過構建 “層次樹”( dendrogram )劃分簇,分為凝聚式(自底向上)和分裂式(自頂向下),常用凝聚式方法。
AGNES算法-自底向上
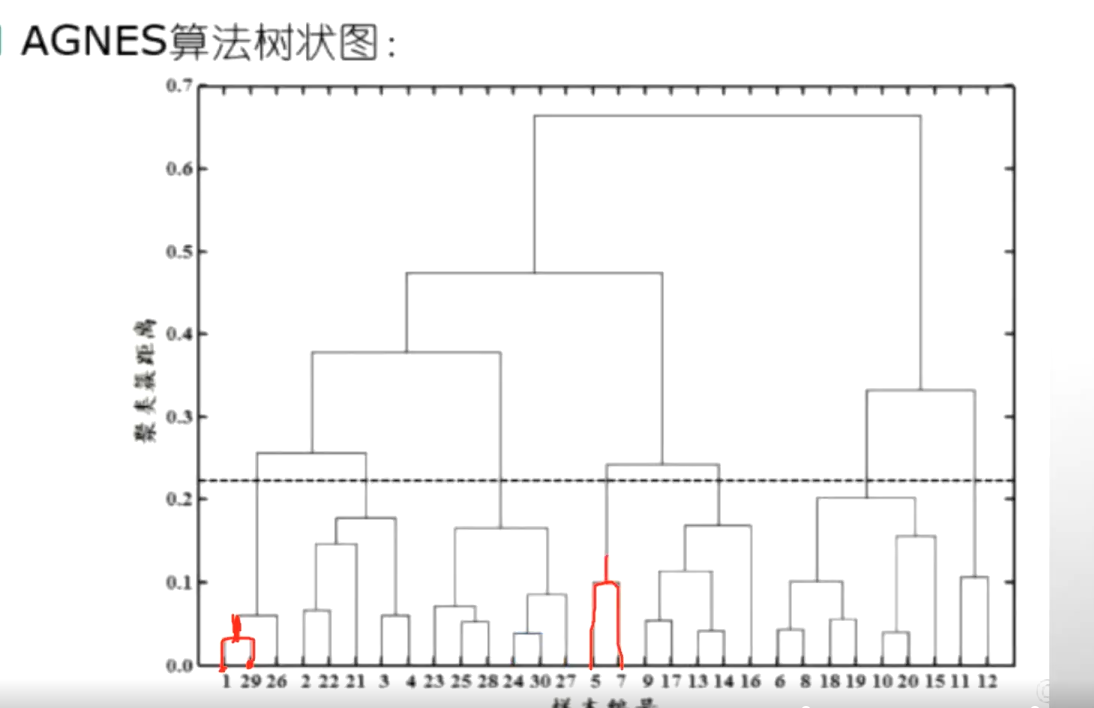
????????現在有一共有30個樣本,那么這30個樣本首先我們去選擇兩兩之間去選擇。兩兩之間進行計算,首先要計算出來最近的兩個樣本,我們發現1和29最近,就把1和29進行合并。合并之后計算它的一個向量均值,得到了一個新的樣本那這樣的話,這個樣本數量從30就變到了29,因為1和29合并了。那么我們再計算這29個和另外的這些兩兩計算它的一個距離。找到其中的最小的值再把它變成合并成為一個新的,那就29變成了28...........這樣兩兩計算的最后越來越小,越來越少,最后就變成了這兩個進行合并變成一類了。
4、代碼實現
import numpy as np
import matplotlib.pyplot as plt# 兩點歐氏距離
def distance(e1, e2):return np.sqrt((e1[0] - e2[0]) ** 2 + (e1[1] - e2[1]) ** 2)# 集合中心
def means(arr):return np.array([np.mean([e[0] for e in arr]), np.mean([e[1] for e in arr])]) # mean用于求取均值 arr存放某一個簇中的點if __name__ == "__main__":## 生成二維隨機坐標(如果有數據集就更好)arr = np.random.randint(0, 100, size=(100, 2))## 初始化聚類中心和聚類容器m = 5 # 聚類個數k_arr = np.random.randint(0, 100, size=(5, 2)) # 隨機初始5個中心cla_temp = [[], [], [], [], []] # 存放每個簇中的點## 迭代聚類n = 20 # 迭代次數for i in range(n): # 迭代n次for e in arr: # 把集合里每一個元素聚到最近的類ki = 0 # 假定距離第一個中心最近min_d = distance(e, k_arr[ki])for j in range(1, k_arr.__len__()):if distance(e, k_arr[j]) < min_d: # 找到更近的聚類中心min_d = distance(e, k_arr[j])ki = jcla_temp[ki].append(e)# 迭代更新聚類中心for k in range(k_arr.__len__()):if n - 1 == i:breakk_arr[k] = means(cla_temp[k])cla_temp[k] = []## 可視化展示col = ['HotPink', 'Aqua', 'Chartreuse', 'yellow', 'LightSalmon'] # 僅提供了5種顏色for i in range(m):plt.scatter(k_arr[i][0], k_arr[i][1], linewidth=10, color=col[i]) # 畫中心的散點圖plt.scatter([e[0] for e in cla_temp[i]], [e[1] for e in cla_temp[i]], color=col[i]) # 畫簇中的點plt.show()if __name__ == "__main__":## 1. 生成隨機數據# 生成100個二維隨機點,坐標范圍在0-100之間arr = np.random.randint(0, 100, size=(100, 2)) # 形狀為(100, 2),100個樣本,每個樣本2個特征(x,y)## 2. 初始化聚類參數m = 5 # 聚類的簇數(K=5)# 隨機初始化5個聚類中心(從0-100中隨機取坐標)k_arr = np.random.randint(0, 100, size=(5, 2)) # 形狀為(5, 2),每個中心是一個二維坐標# 初始化5個空列表,用于存放每個簇中的點cla_temp = [[], [], [], [], []] # 索引0-4對應5個簇## 3. 迭代執行K-Means聚類n = 20 # 迭代次數(可調整,次數越多結果越穩定)for i in range(n): # 迭代n次優化聚類結果# 步驟1:將每個數據點分配到最近的簇for e in arr: # 遍歷每個數據點ki = 0 # 初始假設最近的簇是第0個min_d = distance(e, k_arr[ki]) # 計算當前點到第0個中心的距離# 遍歷其他簇中心,找到更近的中心for j in range(1, k_arr.__len__()):d = distance(e, k_arr[j])if d < min_d: # 發現更近的簇中心min_d = dki = j # 更新最近簇的索引cla_temp[ki].append(e) # 將點分配到最近的簇# 步驟2:更新每個簇的中心(最后一次迭代不需要更新,直接保留結果)for k in range(k_arr.__len__()):if n - 1 == i: # 如果是最后一次迭代,不更新中心,直接跳出break# 計算當前簇的新中心(均值)k_arr[k] = means(cla_temp[k])# 清空當前簇的點列表,為下一次迭代做準備cla_temp[k] = []## 4. 可視化聚類結果# 定義5種顏色,用于區分不同的簇col = ['HotPink', 'Aqua', 'Chartreuse', 'yellow', 'LightSalmon']for i in range(m):# 繪制每個簇的中心(用大圓點表示)plt.scatter(k_arr[i][0], k_arr[i][1], linewidth=10, color=col[i])# 繪制每個簇中的數據點(用小圓點表示)plt.scatter([e[0] for e in cla_temp[i]], # 所有點的x坐標[e[1] for e in cla_temp[i]], # 所有點的y坐標color=col[i])plt.show() # 顯示圖像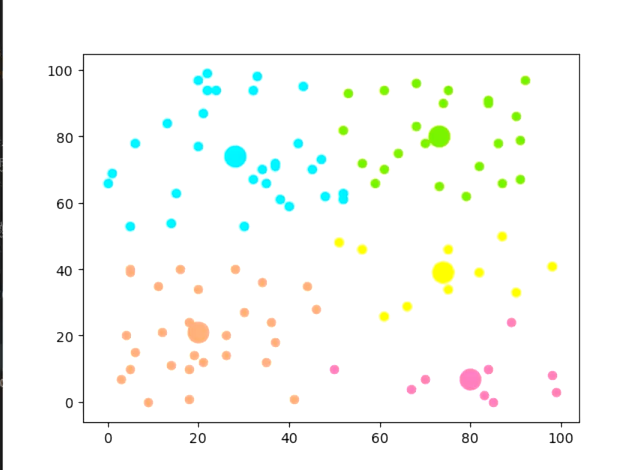
聚成五類
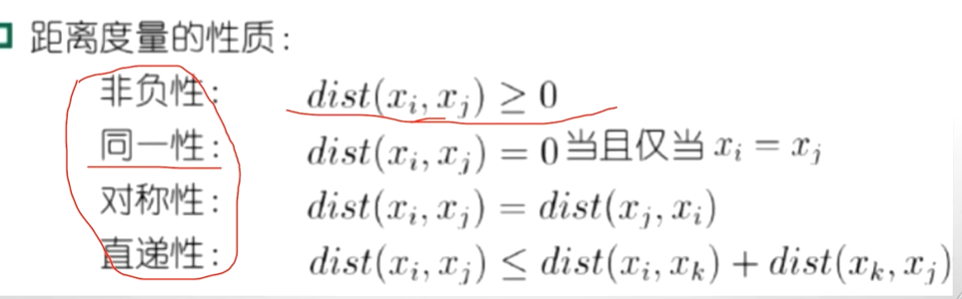








list的模擬實現)










顯示功能)
