本教程總結CS61B 關于圖章節中的最小生成樹(Minimum Spanning Trees, MST)問題,以及對應的的算法
什么是最小生成樹(MST)
考慮這樣一個問題,給你一個無向圖,你能不能找出這個圖中的一組邊,讓其滿足:
- 連通的
- 無環的
- 涉及到了所有的結點
比如這樣一張圖
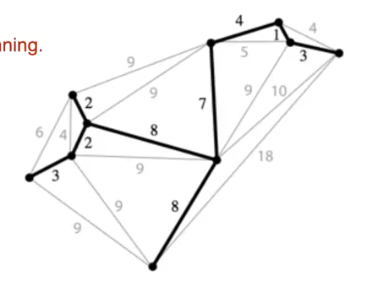
這樣的一組邊構成的樹,稱為生成樹
而讓這個樹中所有的邊權重之和最小即為最小生成樹
如何找到最小生成樹
一個非常有用的性質:割邊屬性(Cut Property)
- 一個 cut 就是將一個圖中的結點分成兩個非空集合
- 一個 crossing cut 就是從一個集合結點連接到了另一個集合結點的邊
割邊屬性是這樣描述的:給定任意一個 cut,最小權重的 crossing edge 一定在最小生成樹中
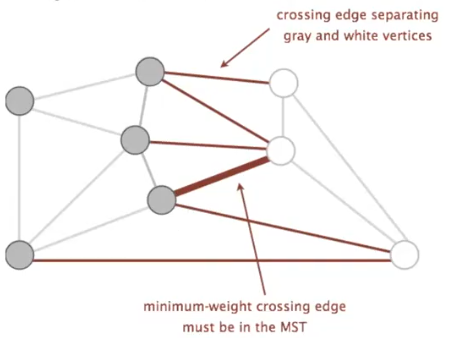
比如上面這張圖中,所有的紅色邊都是 crossing edge,其中最小的邊一定在最小生成樹中
我們判斷 crossing edge 只需要看這個邊是否連接了兩個屬于不同集合(也就是不同顏色)的結點即可
通用的尋找 MST 算法
基于割邊屬性,我們可以這樣構造一個算法:
首先一開始MST沒有邊:
- 找到一個沒有 crossing edge 在MST中的 cut
- 然后將最小權重的 crossing edge 加入 MST
- 一直重復到 V-1 條邊
Prim’s Algorithm
相比較最短路徑樹而言,最小生成樹并不需要給出一個起點,在最小生成樹中,只需要給你圖然后說告訴我哪些邊觸及所有頂點且權重之和最小即可。
但是并不代表我們不選取一個起始結點,相對來說,Prim 算法會隨機選擇一個起始結點,這個隨機性并不對最終結果產生影響(我們總要尋找一個結點來入手)
算法流程
從一個隨機結點開始:
- 將一個一頭連接已經在MST中結點的最短的邊,加入MST,直到 V-1 條邊
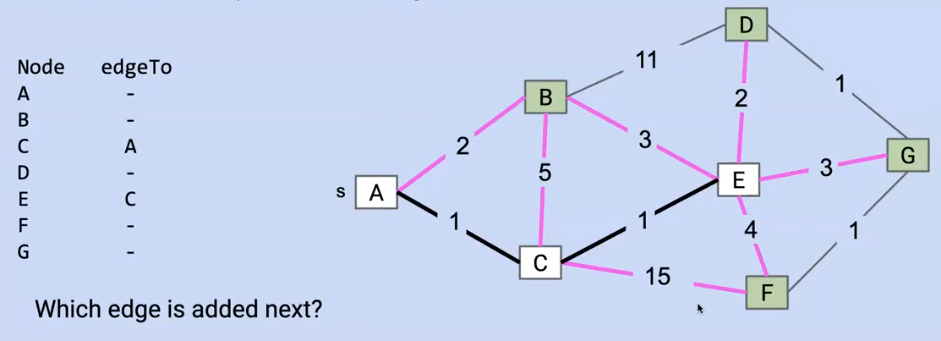
比如在這個圖中,所有符合上述條件的即為紅色的邊:連接了一個在MST中的結點
然后我們選取這些邊中最短的邊,也就是A->B或者E->D
Prim 算法實際上是不斷地使用了割邊屬性
改進的 Prim’s Algorithm
Prim 算法是可以奏效的,但效率太低了,因為你必須考慮大量的穿過這個 cut 的 crossing edge
我們對 Prim 算法進行改進:
- 將所有結點放入 fringe PQ 中,以結點到樹的距離作為排序標準
- 重復:將距離樹最近的結點移出,然后將其指出的所有邊進行relaxation,然后對 distTo 和 edgeTo 數組進行更新
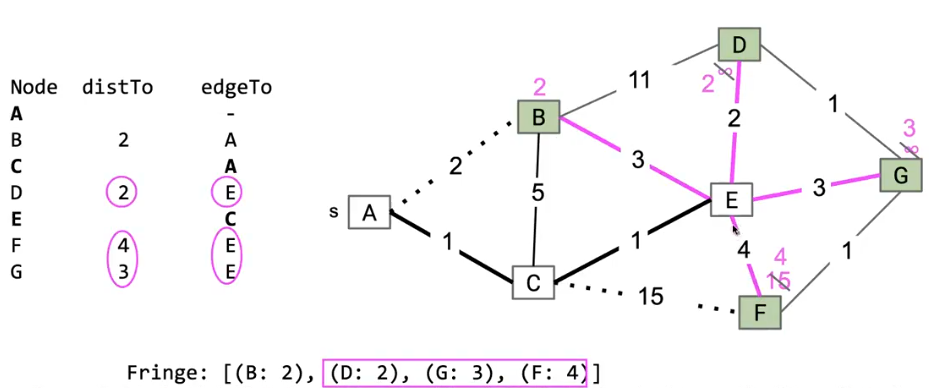
這個圖中我們剛剛把距離樹最近的結點E移出,加入到MST中,然后relax它的所有的邊,同時更新 distTo 和 edgeTo 數組
圖中加粗的邊為MST中的邊,圖中的虛線表示relax出來的邊,作為MST的候選邊,如果在relax中發現這條邊不如之前的邊(比如C->B),或者這條邊被后續的邊所取代(比如下一步的C->F即將被E->F取代),那么這條邊我們甚至不標注為虛線
而如果在MST中的邊被新邊取代,那么我們把新邊加入MST,原來的邊回到最開始的模樣(不加粗,也不標為虛線)
同時我們看到 Fringe 中的結點是按照到樹的距離進行排序的,同時 distTo 數組也變為了到樹的距離
算法實現
public PrimMST{public PrimMST(EdgeWeightedGraph G){edgeTo = new Edge[G.V()];distTo = new double[G.V()];marked = new boolean[G.V()];fringe = new SpecialPQ<Double>[G.V()];distTo[s] = 0.0;setDDistancesToInfinityExceptS(s);insertAllVertices(fringe);while(!fringe.isEmpty()){int v = fringe.delMin();scan(G,v);}} ....private scan(EdgeWeightedGraph G, int v){marked[v] = true;for(Edge e: G.adj(v)){int w = e.other(v);if(marked[w]){continue;}if(e.weight() < distTo[w]){distTo[w] = e.weight();edgeTo[w] = e;pq.decreasePriority(w, distTo[w]);}}}
}
Kruskal’s Algorithm
按照權重順序考慮所有的邊,只要這條邊加入MST后不構成環,那么就將它加入MST中,重復直到 V-1 條邊
Kruskal 算法計算過程中創造出的MST可能是割裂不連續的,但是沒關系,最后會得出正確的結果
我們可以通過維護兩個輔助數據結構來幫助我們實現:
- WQU 加權快速集合:幫助我們判斷是否有環生成
- MST :統計最小生成樹的邊
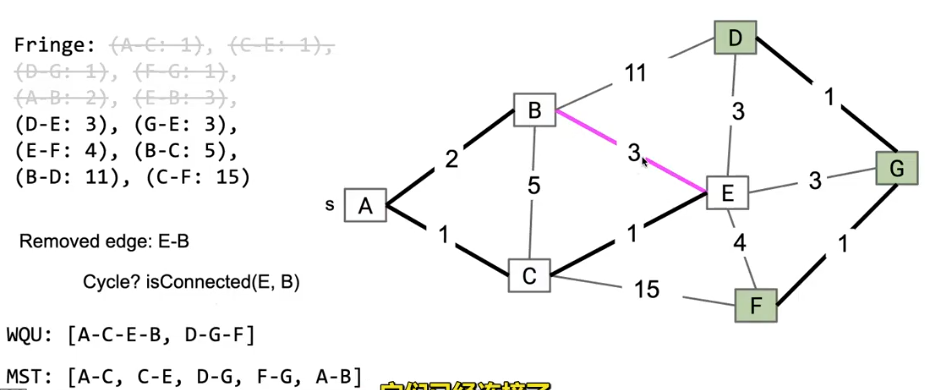
在這個圖中我們按順序從 Fringe 中取出對應的邊,當我們即將取出E->B這條邊時,WQU告訴我們已經有了一條從E到B的路徑,也就是下一步即將成環,所以我們不考慮E->B這條邊
算法實現
public class KruskalMST{private List<Edge> mst = new ArrayList<Edge>();public KruskalMST(EdgeWeighedGraph G){MinPQ<Edge> pq = new MinPQ<Edge>();for(Edge e: G.edges()){pq.insert(e);}WeighedQuickUnionPC uf = new WeighedQuickUnionPC(G.V());while(!pq.isEmpty()){Edge e = pq.delMin();int v = e.from();int w = e.to();if(!uf.connected(v,w)){uf.union(v,w);mst.add(e);}}}
}





)

)

)
)



 動火安全作業證)




