中國古代數學符號的演進 | 算籌 / 符號 / 算法

注：本文為“中國古代數學符號”相關合輯。

圖片清晰度受引文原圖所限。
略作重排，未整理去重。
如有內容異常，請看原文。

這個中國古代的數學瑰寶，到底厲害在哪？

原創朱一文科普中國 2024 年 07 月 31 日 15:30 北京

中國古代數學源遠流長，《九章算術》作為漢代成書的重要數學著作，歷來被稱作“算經之首”。已故中國科學院院士、著名數學家吳文俊先生（1919-2017）曾指出：“《九章算術》及其劉徽注，在數學發展史上具有崇高的地位，足以與古希臘歐幾里得《幾何原本》東西輝映，各具特色。”那么，《九章算術》究竟有哪些數學成就，又為何在數學史上有如此高的地位呢？

算籌與準十進制位值制記數法

《九章算術》總結了先秦以來的數學成就，其中最重要的數學成就是算籌的準十進制位值制記數法。所謂十進制（decimal system），是從 1 開始記數，到 10 換一個記數方式；而位值制（place - value system）是指同一個數字放在不同位置，具有不同的數量含義。古埃及數學采用十進制記數法，但并非位值制（而是壘數制）；古巴比倫數學采用位值制記數法，但使用的是 60 進制。現代的印度 - 阿拉伯數字是十進制位值制，而從文獻記載來看，其晚于中國算籌記數。因此，新加坡學者藍麗蓉（Lam Lay Yong）甚至提出印度 - 阿拉伯數字可能起源于中國算籌的說法。2016 年，中國科學院自然科學史研究所編寫的《中國古代重要科技發明與創造》一書，明確將這一成就列入其中。

算籌在中國使用了約 2000 年，直到 16 世紀被算盤取代之前，一直是中國人長期使用的數學工具，也是日本、朝鮮、越南、琉球等漢字文化圈國家長期使用的數學工具。其材質通常為竹子（也有象牙、骨、鉛、銀等），漢代的算籌長約 12 厘米。近代以來，多地有算籌出土，例如 1983 年 11 月在陜西省旬陽地區漢墓出土了 28 根象牙算籌。日本也藏有算籌。在古語中，“筭”與“算”不同，前者指擺弄竹子，即算籌；后者指裝算籌的器物，引申為計算。因此，古書中普遍寫作“筭術”（即運用算籌的算法），例如《九章筭術》。


陜西旬陽出土算籌	日本東大寺所藏算籌

算籌記數分為縱橫兩式，個、百、萬等位上用縱式，十、千、百萬等位上用橫式。例如，數字 12345 擺放為 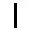12345 的算籌表示。由于十位上的 1 和個位上的 1 擺放不同，因此這種記數法被稱為“準位值制”。這一特點體現了算籌記數的優勢：遇 0 作空位處理，縱橫不同的擺放方式可以最大限度凸顯空位，例如 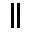203 的算籌表示表示 203，而不可能是 23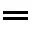（ 23 的算籌表示 )。《九章算術》卷八方程涉及正負術，通過算籌的顏色和擺放方式也可以區分正負。

正負術示意圖

以算法為中心

《九章算術》全書分為九卷，包含 246 個數學問題。學界曾存在誤解，認為該書是一本應用問題集，但實際上，246 個問題對應的算法（即“術”）僅有約 100 個，多個問題往往對應一個算法。因此，數學史家郭書春指出，該書采用的是“術文統率例題”的形式。另有誤解認為該書是一本算法操作手冊，運籌者無須理解其中的數學原理。然而，數學史家李繼閔指出，算法實施過程中蘊含著算理（即“寓理于算”），不懂數學原理實際無法進行計算。

吳文俊先生指出，中國古代的算法具有構造性和機械化的特點。構造性與現代存在性數學相對應，指算法往往給出求解路徑；機械化則體現在籌算過程。法國學者林力娜（Karine Chemla）通過大量文獻分析，指出《九章算術》及其劉徽注的數學問題、圖和棊等幾何工具以及算籌的實施，都是展現算法的工具，從而有力地證明了以《九章算術》為代表的中國古代數學是以算法為中心的數學。從世界數學史角度看，除了古希臘數學以外的其他數學文明都具有算法傾向，丹麥數學史家休儒（Jens H?yrup）進一步認為中國數學是所有文明中最重視算法的。學界以往多認為《九章算術》具有實用性和社會性的特點，其實這一特點其他數學文明也具備，唯有對算法的高度重視是中國古代數學的獨特之處。就此而言，《九章算術》可視作一本理論數學著作。

《九章算術》各卷內容如下：

卷一方田：給出籌算分數的計算法則和各種田面積的計算公式，其中圓面積公式為“半周乘半徑得積步”，即 $\pi r^2$ ，這一公式巧妙地回避了圓周率，是完全準確的。
卷二粟米：給出各種谷物的換算，其中提出“今有術”，即已知三個數求成比率的第四個數，這一算法在西方被稱作“三率法”。
卷三衰分：講述各種物品的比例分配問題。
卷四少廣：涉及土地的丈量和劃分，給出用算籌開平方和開立方的算法，這一方法在宋代發展成普遍求任意一元高次方程數值解的算法，與現代數學中的牛頓法類似。
卷五商功：處理工程問題，涉及各種幾何體的體積計算問題，提出三種基本幾何體（立方、塹堵和陽馬）作為求解任意幾何體體積的基礎。立方即正立方體；塹堵是底面為等邊直角三角形的三棱錐，兩塹堵合成一立方；陽馬是底面為正方形，一棱與底垂直的四棱錐，三陽馬合成一立方。
卷六均輸：關于稅收的比例分配問題。
卷七盈不足：通過兩次假設求解問題的算法，該算法在西方被稱作“雙假設法”。由于該法可以把任何問題理解成線性問題，進而求出解答，故也稱為萬能算法。
卷八方程：求解多元一次線性方程組的完整算法，其中給出涉及該問題時必須用到的正負術法則。例如第一問：

今有上禾三秉，中禾二秉，下禾一秉，實三十九斗；上禾二秉，中禾三秉，下禾一秉，實三十四斗；上禾一秉，中禾二秉，下禾三秉，實二十六斗。問：上、中、下禾實一秉各幾何？答曰：上禾一秉九斗四分斗之一，中禾一秉四斗四分斗之一，下禾一秉二斗四分斗之三。

按術列出如下方程，其求解過程類似現代的矩陣方程解法。清末現代數學傳入中國后，李善蘭借用古語“方程”翻譯“equation”，實際改變了方程的原意。
卷九勾股：講述平面圖形的面積計算問題，給出勾股定理及其各種變化形式。

給出算法正確性的論證

劉徽注《九章算術》

《九章算術》文本中只給出算法，而沒有其正確性的證明。這一特點曾被用作中國數學不如以《幾何原本》為代表的古希臘數學的論據，但現代數學史研究已證明這一觀點站不住腳。首先，除了古希臘數學以外的數學文明，往往只給出算法而沒有證明。吳文俊先生認為數學史是算法傾向與演繹傾向兩大主題此消彼長形成的。其次，文本中是否有證明取決于文本的性質和語境，文本中沒有證明并不代表數學實踐中也沒有證明。最后，林力娜等學者認為不應以古希臘的數學證明作為證明的唯一形態，其他文明中也有不同形態的證明。劉徽注可以驗證這后兩點。

魏景元四年（263 年），劉徽注解了《九章算術》，對大部分術文都給出其算法正確性的論證。例如，在卷一對圓面積公式的證明、卷四對球體積公式的注解、卷五對陽馬體積的證明中，劉徽用到極限逼近的推理方法，展現了極高的邏輯推理能力。在卷四求解球體積公式的過程中，劉徽發明出牟合方蓋，但無法求出其體積，故“以俟能言者”。這一問題最終被祖沖之父子解決。劉徽對幾何問題的證明需用到圖（平面問題）和棊（立體問題），其推理原理被吳文俊總結為“出入相補原理”。

《九章算術》的影響與歷史地位

《九章算術》在唐宋時期均為國子監算學館的教科書。劉徽之后，唐李淳風、北宋賈憲、劉益、蔣周、南宋秦九韶、楊輝、金李冶、元朱世杰等均沿著《九章算術》的路線發展中國古代數學，并使其在宋元時代達到一個高峰。明清時期，中國數學發展的主流雖發生改變，但《九章算術》的整體框架并未改變。日本數學則在中國宋元數學的基礎上發展出和算，在 19 世紀時可以處理面積求和等微積分初等問題。

自李儼（1892-1963）、錢寶琮（1892-1974）先生開創中國數學史研究以來，《九章算術》及其后世注解就作為中國數學成就的標志性著作。他們主要關注其中與現代數學相通之處，但實際上，《九章算術》中那些獨特算法同樣是中國數學的偉大成就。兩者共同說明了中國數學歷史道路的獨特性和其歷史經驗的有效性。

吳文俊先生將中國古代數學的算法理解成計算機的軟件，將算籌、算盤等工具理解成計算機的硬件，從而創造性地提出數學機械化的構想，這是中國古代數學“古為今用”的典范案例。

策劃制作

本片為科普中國?創作培育計劃扶持作品
出品丨中國科協科普部
監制丨中國科學技術出版社有限公司、北京中科星河文化傳媒有限公司
作者丨朱一文科學技術史博士，中山大學哲學系教授、博士生導師，邏輯與認知研究所專職研究員
策劃丨林林
責編丨林林鐘艷平
審校丨徐來

從刻痕與結繩到現代數學符號，人類如何創造語言的另一種奇跡

原創遇見數學科學演繹法 2024 年 11 月 27 日 20:05 河南

數學是一種獨特的語言，它以簡潔而精準的符號揭示自然規律，并幫助人類探索不可見或抽象的領域——從微觀粒子到宏觀宇宙，從無窮到高維空間，甚至復雜的邏輯結構。數學符號的誕生與發展是人類智慧的結晶，也是科學和技術進步的基石。今天，我們走近數學符號的世界，了解它是如何誕生、如何運作，以及為什么它如此重要。

數學符號的重要性

數學符號是用來表示數學對象、運算、關系和邏輯規律的符號體系，包括數字、變量與常量、運算符、關系符及各個不同數學分支中的特殊符號。數學符號的力量在于其簡潔性和通用性。它超越了語言的障礙，成為科學家、工程師和數學家共同的交流語言。

愛因斯坦的著名公式 $E = mc^2$ 是一個典型例子。當愛因斯坦提出質量和能量之間的關系時，他借助這一公式，將一個復雜的物理概念濃縮成簡短的表達式。沒有這些符號，就需要用一整段話甚至幾頁文字來描述這個等式的含義。

數學符號不僅簡潔，還具有通用性。無論是中國人、法國人還是印度人，公式 $E = mc^2$ 或 $a^2 + b^2 = c^2$ 的意義都是一致的。數學符號超越了語言和文化的障礙，成為全球通用的交流思想的工具。

不僅如此，數學符號還具有抽象性，能夠描述自然語言難以企及的深刻概念和復雜邏輯。例如，邏輯表達式 $\forall \; x \in \mathbb{R}, \exists\; y \in \mathbb{R}, y > x$ 用符號精確地表達了“對于任意一個實數 $x$ ，總存在一個比它大的實數 $y$ ”的數學思想。這種抽象能力使得數學不僅可以研究具體的對象，還能深入研究邏輯關系、集合結構甚至高維空間的性質。

數學符號的價值還在于其普適性。它不僅是科學研究的工具，更是思想的載體。正是通過這些符號，數學家得以將復雜的概念形式化，進而探索更遠的未知領域。

數學符號的起源與演化

數學符號的演化史是人類智慧發展的縮影。從最早的計數工具到今天復雜的公式，數學符號經歷了漫長而有趣的發展過程。數學符號的歷史可以追溯到人類文明之初，隨著人類對數學的理解不斷深化，符號才逐漸被抽象和系統化。

早期的計數和符號萌芽

數學符號的歷史可以追溯到數萬年前。當時，所謂的數學活動主要是計數，最古老的數學工具是簡單的刻痕、結繩或小石頭，這些原始的符號雖然簡單，但標志著人類開始嘗試用外部工具記錄和表達數學思維。

在這里插入圖片描述

例如：

伊尚戈骨（約 20,000 年前）：一塊來自非洲的骨頭，上面刻有規律的刻痕，被認為可能是早期的計數工具。
繩結記事法：安第斯山脈的印加文明使用“結繩”記錄數字和信息，這種方法被稱為“基普”。

隨著文明的進步，數字符號逐漸出現。巴比倫人發明了用楔形文字記錄數字的方式，發明了基于 60 進制的計數系統。而古埃及人則用象形符號表示數量。這些早期符號盡管原始，卻標志著數學思維的萌芽。

零的出現：數學符號史上的里程碑

數位的概念和零的發明是數學符號發展史上的重要一步。因為在此之前，零的概念并不存在。

巴比倫人（約公元前 2000 年）：最早使用零作為占位符。例如，數字 306 中的“0”表示“沒有十位數”。
印度數學家（約公元 5 世紀）：率先將零視為一個獨立的數字，并用點或圓圈表示。這一創新被阿拉伯數學家傳播到全世界，極大推動了數學的發展。

在這里插入圖片描述

零的出現不僅解決了數字記錄的難題，還為現代數學、科學和工程領域奠定了基礎。沒有零，代數、微積分乃至計算機科學的發展都將無從談起。

16 世紀：數學符號化的轉折點

數學符號的系統化發展始于文藝復興時期。在 16 世紀之前，數學的表達方式與今天我們熟悉的符號化數學有著天壤之別。幾乎所有的數學思想、計算步驟和證明過程都通過自然語言敘述，而不是符號化的表達。例如，古希臘數學家歐幾里得在《幾何原本》中使用長篇敘述來陳述幾何定理，而非符號化的表達方式。

在這里插入圖片描述

正是在這種背景下，部分數學家嘗試用更簡潔的形式表達數學思想。其中，丟番圖（Diophantus） 是重要的先驅之一。他的著作《算術》（Arithmetica）中，開創性地引入了一些符號化的方法，以簡化數學表達：

用符號表示未知數。例如，丟番圖用一種特殊的符號（類似希臘字母）來表示未知數，而不是用完整的文字描述。
使用縮寫表示某些數學運算。例如，他用一種簡寫的形式表達平方和平方根運算，而不是通過詳細的句子。

這標志著數學符號化的早期嘗試。然而，由于丟番圖的符號體系并未被廣泛傳播，因此直到文藝復興時期，這種符號化的思想才被再次發展和推廣。

現代數學符號的誕生

在這里插入圖片描述

數學符號的系統化始于文藝復興時期：

弗朗索瓦?韋達（Fran?ois Viète）（16 世紀）：首次使用字母表示未知數，開創了代數學符號化的先河。
笛卡爾（René Descartes）（17 世紀）：引入了我們今天熟悉的符號，比如用 $x, y, z$ 表示未知數，用 $a, b, c$ 表示已知量。他還提出了復數單位 $i$ 的概念。

18 至 19 世紀的標準化

萊布尼茨與牛頓：分別提出了微積分的符號體系。萊布尼茨的積分符號 $\int$ 和微分符號 $d$ 至今仍在使用。
隨后，歐拉（Leonhard Euler） 在 18 世紀對數學符號進行了進一步的完善。他發明或推廣了許多我們今天熟知的符號，例如函數表示法 $f (x)$ 、自然對數的底數 $e$ 和圓周率 $\pi$ 。

隨著數學的全球化傳播，符號逐漸被標準化。統一的符號體系不僅縮短了數學家之間的交流時間，還推動了數學思想的迅速傳播。

盡管數學符號的基礎體系在 18 世紀已經確立，但發展并未停止。隨著探索數學的不斷深入，許多新符號還在引入以應對復雜的數學需求。

現代符號的擴展

隨著數學分支的擴展（如拓撲學、統計學和量子力學），新的符號也不斷被創造出來。例如，拓撲學中，符號 $\partial$ 描述了邊界運算；量子力學中使用了狄拉克符號（如 $\psi \rangle$ 和 $\langle \psi |$ ）來表示量子態。

結語：數學符號的魅力

數學符號是人類智慧的結晶。它不僅是科學交流的工具，也是我們探索世界奧秘的鑰匙，是人類文明進步的縮影。當你下次看到復雜的數學公式時，不妨換個視角。試著去理解這些符號背后的故事和邏輯，它們不是冷冰冰的字符，更是通往知識殿堂更深處的橋梁。

位置示數法：一種具有代數符號功能并具優勢的中國傳統數學方法

鄒大海、夏慶卓返樸 2025 年 02 月 16 日 08:30 北京

代數符號的引入與使用，對數學的發展具有重大的促進作用。中國古代的籌算采用了一種位置示數法，具有代數符號的功能。它不僅借助位置來表示數，而且用位置來表現各種未知數及其不同次數的冪，還利用相對位置的調整來實現代數運算的功能，且在某些方面更具優勢，充分展現了中國傳統數學的特色。將中國傳統數學的位置示數法與現代數學的符號代數法結合，有可能為數學的發展提供新的思路。

撰文 | 鄒大海（中國科學院自然科學史研究所）、夏慶卓（中國科學院自然科學史研究所、中國科學院大學）

用代數符號來表示未知量或可變量，對于數學的發展具有重要的意義。[注釋 1] 成套的數學符號是 16 世紀以來在歐洲首先發展起來的 [1]。在西歐數學傳入以前，中國傳統數學很少使用代數符號，但代數學卻是很發達的。究其原因，中國古代的哲人充分發掘位置在數學中的重要作用 [注釋 2]，開發出了一套用位置標示數學含義的方法，可以實現后來近現代數學中代數符號的功能 [注釋 3]，這種方法我們稱為位置示數法。之所以不稱 “位置代數法”，是因為古代并不是讓一個位置本身一定代表一個數或未知量，而只是強調這個位置被用來賦予在該位置或其附近位置上所放置的數據的含義。位置示數法，不僅造就了最早的十進位值制記數法，而且利用位置標示不同的未知數或未知數的冪，進而通過簡單操作實現代數運算的功能。本文揭示，比之近現代數學中的代數符號及其運算，中國古代的位置示數法還未發展出那么豐富的功能，就已經在相當長的時期內失傳，但它在某些方面卻更具優勢。本文提出，將中國傳統數學中充分發揮位置功能的思想和方法與現代數學的符號表示法結合起來，借助現代計算機技術，或許可以為現代數學的發展提供新的思路，從而為中華優秀傳統科技文化在新時代的弘揚，提供一個新的契機。

1 算籌與籌算

中國傳統數學對位置的開發利用，始于算籌記數法。算籌是中國古代長期用來記數和計算的工具。古人用算籌來進行記數、表示數量關系，并進而以此為基礎進行演算。這些使用算籌的活動和相應的方法，叫做籌算。位置示數法，就是基于籌算語境而發展起來的數學方法。當然，這種方法后來也在珠算中發揮作用。

算籌又稱算、籌、策、籌策、算子等。算籌本身非常簡單，就是長條形小棍，材質有竹、木、金屬、骨頭乃至象牙等，但主要是竹和木，尤以竹質為多，所以表示算籌的字往往從竹。

算籌記數包括兩個方面。一方面，用算籌表示 1-9 的基本數字時，有縱、橫兩種形式：

表 1

其中，對于 1 至 5，表示幾就用幾根算籌；對于 6 至 9，用一根放在上面的算籌表示所含的 5，比 5 多幾就在下面用幾根算籌與表示 5 的算籌垂直靠攏放置。另一方面，用算籌表示十進制整數時，個、百、萬等奇數位用縱式，十、千、十萬等偶數位用橫式，縱、橫交錯擺放。若某位上數字為零，則空出相應的位置。如 68012 用算籌表示即 [2, 4-7]。此外，古人席地而坐，個位數字擺放在右膝蓋正前方的位置，這樣就可以很方便地對末幾位全為零的數（如 560、5600）進行區分。

算籌記數可以追溯到原始社會以草莖、小棍記數，上述算籌記數制度應出現于西周和春秋之交而可能更早。這種記數法，只用 9 套符號（每套縱、橫 2 個，同一數字橫式和縱式視為一個的話則只是 9 個符號）就可以表示任意的自然數，是世界上最早的典型的十進位值制記數法。除符號形式外，它與今天的印度 - 阿拉伯數字記數法相同，而早于后者至少數百年。不僅如此，古人還通過算籌的顏色（紅、黑）、形狀（截面為三角形、長方形）或擺放方式等來表示正負數。[2, 4-7]

2 位置的數值功能

前面已經說到，中國古代的算籌記數法采用十進位值制。在這記數系統中，同一個數字符號 $a$ 放在不同的數位，表示不同的數值：在個位表示 $a$ ，在十位表示 $a$ 個十，在百位表示 $a$ 個百。數字擺放所處的位置，標示相應的數字單位，這是位置在中國古代數學中最常見和直觀的功能，它也一直沿用于現代的世界各地。當然，中國古代的算籌記數法所擺成的符號與印度 - 阿拉伯數碼形狀不同，而后者在不同時代和地區的寫法，也有所變化。

3 位置的未知量功能

中國古代數學中，位置也具有標識未知數的功能。當然，這種功能是通過一定的規則來實現的。首先看現在常用的線性方程組及其解法，中國古代早在兩千多年前就有相應的列法和解法，就稱為 “方程”，《九章算術》專設第八章 “方程” 章來處理這類問題。不過，古人不用符號表示未知數，而是用不同的位置來體現不同的未知量或常數。如第一題是：

今有上禾三秉，中禾二秉，下禾一秉，實三十九斗；上禾二秉，中禾三秉，下禾一秉，實三十四斗；上禾一秉，中秉二秉，下禾三秉，實二十六斗。問：上、中、下禾實一秉各幾何？[9]

其中 “秉” 是量詞，表示把、束。“禾” 是從田間粟的植株收割下來帶有莖葉和谷穂的部分，“實” 是從禾上打下來的谷子。這個問題假設有上、中、下三等禾，已知它們的秉數的 3 種組合，各得到已知數量的谷子（體積），要求出每等禾一秉分別能打下多少谷子。按現代的方法，可設每秉上等禾、中等禾和下等禾打出的谷子分別為 $x$ 斗、 $y$ 斗和 $z$ 斗，那么由題設中每組已知條件可分別列出一個代數方程式。把 3 個代數方程式聯立起來，就得到一個線性方程組：

$\begin{cases} 3x + 2y + z = 39 \quad(1)\\ 2x + 3y + z = 34 \quad(2)\\ x + 2y + 3z = 26 \quad(3) \end{cases}$

《九章算術》用算籌將三個等量關系表示成右、中、左三列數，形成一個方程，如圖 1-1；如果把算籌符號換成現代的印度 - 阿拉伯數字，便得到圖 1-2。可以看出，只要把圖 1 的豎列變成橫行，則與現代的增廣矩陣并無二致。所以古代的方程是一種采用類似于現代增廣矩陣的簡單形式，它只用幾組數就構成一個整體，這個整體對應于一個聯立線性方程組。

這種表示法的核心是將等量關系中的具體數字按特定的順序進行排布：

（1）各個等量關系中諸未知量的倍數（即現代數學中未知量的系數），在擺放到表示這些等量關系的各列中時都具有相同的順序。按現代的說法，就是將各列中 $x$ 、 $y$ 、 $z$ 的系數都分別放置于從上至下的第一、二、三個位置。可見，各系數所處的位置具有表示相應未知量的功能。

（2）各個等量關系中的常數項總是放在對應列中的最下位置。也就是說，最下位置具有標示常數項的功能。

因此，盡管當時沒有使用未知量的符號，也沒有把常數項與未知項用可見的符號區分開來，卻通過無形的位置把它們都標識了出來，實現了近一千七八百年以后才采用的代數符號的功能。這種 “方程” 的表達方式與歐洲兩千年后用分離系數法表示線性方程組的增廣矩陣在形式和結構上都極為相似。不僅如此，中國上古時代 “方程” 的求解變換，與增廣矩陣的變換也是非常相似的。古代 “方程” 是增廣矩陣的一個太過早熟的先驅。法國科學院院士、曾任蘇黎士大學數學系主任的 P. Gabrieal 編寫的教科書《矩陣、幾何、線性代數》（Matrizen, Geometrie, Lineare Algebra）第 2 節題為 “方程算法”（Der Fang-Cheng Algorithmus），將處理線性方程組的增廣矩陣方法稱為 “方程法”（Fang-Cheng-Regel），取代了以前的流行稱謂 “高斯消元法” [10]。另外，正是由于 “方程” 這種特殊的結構與表達方式，導致了中國早在戰國時代就引入了正負數概念，并能順利地進行正負數的四則運算，而沒有陷入歐洲直到 19 世紀還存在的關于負數合法性的糾結中。[7, 11]

4 位置指示未知數的冪

對于一元多項式或一元高次方程，中國古代不用未知數符號，自然也就沒有符號來表示未知數的冪。古人想到的辦法，還是通過位置來區分。他們將表示某個數的算籌放置在特定的位置，來表明它是未知數若干次冪的倍數（或標示它為常數項）。例如在宋金元時期，對于一元高次方程，通常將常數項、一次項、二次項直到最高項的系數從下至上排列（也有反過來排列的）就可以把它表示出來。

也就是說，從下至上的位置對應著已知數（常數，按現代的說法也可以說是未知數的 0 次方）、未知數的一次方、未知數的二次方、…、未知數的最高次方。而一個位置上放著表示某數的算籌，表示這個數與該位置表示的未知數的冪相乘，

或表示放在該位置的數為已知數（也可以說是該數與未知數的 0 次方相乘）。圖 2-1 是《測圓海鏡》卷 3 第 5 題的算草中列出的帶從開方式，把算籌符號改為印度 - 阿拉伯數字后即圖 2-2，相當于一元三次方程 $x^3 - 336x^2 + 5184x + 2488320 = 0$ 。如果有必要，古人也在標示一次項的位置的旁邊放置一個 “元” 字或在常數項的旁邊放置一個 “太” 字 [5]，以避免混淆，這是方程式在當時的籌算表達式中唯一出現的符號，它們是數學符號但不能算是代數符號，它們與現代的代數符號只有一點點相似。因為，無論是 “元” 字還是 “太” 字，都并不表示具體的某個數或某個未知數，它們只是標示它旁邊的位置（而不是它自己所在的位置）上所放的數是一次項或常數項。

在對應于一元三次方程式 $x^3 - 336x^2 + 5184x + 2488320 = 0$ 的籌算表達式圖 2-1 中，在一次項系數（從下往上第 2 個數）的旁邊放一個 “元” 字就得到圖 3-1，在常數項（最下位置）的旁邊放置 “太” 字就得到圖 4-1。需要注意的是，這里的 “元” 字或 “太” 字，在當時的籌算操作中，是寫在一個卡片上的，解題者可以隨時根據需要移動它。

5 一個操作，一組運算

位置標示未知量或其冪的方法，不光比符號表示法簡單，而且在計算過程中具有相當的優勢。比如，上述圖 3-1 表示的一元三次方程式 $x^3 - 336x^2 + 5184x + 2488320 = 0$ ，如果方程兩邊同時乘以 $x$ ，在把每一項都乘以 $x$ 時，用現代的代數

符號表示法需要把每一項都重新寫一遍，得到 $x^4 - 336x^3 + 5184x^2 + 2488320x = 0$ ，而中國古代就簡單多了，只需要將 “元” 字卡片向下移動一位就可以表示出來（圖 5）；如果是將原方程兩邊除以 $x$ ，現代的符號表示法需要把每一項重新寫一遍，

成為 $x^2 - 336x + 5184 + \frac{2488320}{x} = 0$ ，而中國古代則只需把 “元” 字向上移一位即可（圖 6）。實際上，如果要乘以（除以） $x$ 的 $n$ 次方，則只要將 “元” 字向下（向上）移動 $n$ 位即可。這種簡單的數學操作，比今天利用代數符號做運算，有很大優勢：一是不需要每一項都寫，要省事得多也簡單得多；二是更不容易出錯。可見，古代這種移動位置的簡單操作，相當于方程的每一項都乘以或除以未知數的冪，起到了進行一組運算的功效；而且方程的項數越多，其優勢就越明顯。同樣地，古人有時不用 “元” 字標識未知數的一次項，而是用 “太” 字標識常數項，也可以通過移到 “太” 字的位置來做類似的乘除運算。

除了多元一次方程組和一元高次方程，宋金元時期的數學家發展出二元、三元和四元的高次方程組。如元代數學家朱世杰利用下、左、右、上四個方向上不同的位置，標示天（ $x$ ）、地 ( $y$ )、人 ( $z$ )、物 ( $w$ ) 四個未知數的相應次數的冪以及它們的乘積（如圖 7 所示），從而利用具有分離系數法功能的位置示數法可以表示多至四個未知數的多元高次方程組，并通過 “上升下降”、“左進右退”、“剔而消之”、“余籌易位” 之類的操作，進行消元和變換，予以求解。

中國古代數學充分發掘了位置的功能，不僅有位值觀念，還用來表示未知數和它們的冪及其乘積，取得了后來符號代數的功效，這種傳統方法甚至在乘以、除以未知數的冪等方面還明顯優于后來的符號代數方法。其中蘊含的創造精神和深刻思想，可以為今天的數學研究提供借鑒。

6 中國古代位置示數法的現代價值

中國社會在清末民初發生劇變，出現所謂 “三千年未有之大變局”，整個知識體系發生從傳統向現代的轉型，數學也是如此。從知識體系和表達方式上看，中國現代的數學在總體上是引進的，但這并不意味著中國傳統數學在現代消失了，它實際上是已融入到現代的數學體系中。比如十進位值制、九九、四則運算、比和比例、盈不足術、開方、面積和體積計算方法等。這些數學知識已成為今天人們工作和生活中一些基本的知識和觀念，只是由于表達形式上的差異、數學教學中鮮有講述其來源等原因，造成今人對中國古代數學的疏離感，所以現代人就很少知道其源于中國傳統數學。因此，我們建議，在今天的教科書和教輔材料中，在教師的教學工作中，要把這些數學知識和數學方法的中國古代來源講述清楚，并指出包括位置示數法在內的一些中國古代數學的方法和思想在某些方面的先進性。這既是對歷史事實和古代先賢的尊重，也有助于激勵年輕學子的文化自信，避免數典忘祖之憾。

中國傳統數學內容豐富多彩，其中有些方法和思想，由于年代久遠和中國學術從傳統向現代的轉型而湮沒不彰。這種情況并不都是優勝劣汰的結果。歷史的淘汰有其復雜性，中國傳統數學的歷史也是如此。比如，被稱贊為 “精妙” 的祖沖之《綴術》在宋代失傳，而宋元時代的重要成就天元術、四元術等也在明代沒有得到繼承，都是水平高卻被淘汰的例證。這些先進數學知識失傳的原因是多方面，其中一個原因反而是它們超越同時代絕大多數人的水平。既然被淘汰的不一定是落后的，那么如果我們仔細考察中國古代數學的思想和方法，就可以從中發現和汲取先進的營養，為今所用。在這一方面，吳文俊先生已經做出了表率。

1974 年春，在特殊的歷史條件下，吳文俊開始學習中國古代數學史。經過兩年多時間的研習，他形成了自己關于中國古代數學特征的認識。他認為，“中國古代數學基本上是一種機械化的數學”。中國古代算法不僅具有程序化、機械化和構造性特征，而且具有重視列方程、解方程的傳統，并形成了系統的方法和理論，同時也發展出了幾何代數化的思想方法，吳文俊對此有深刻的認識，從而大大啟發了他在機器證明數學定理方面的研究。從 1976 底至 1977 年初，吳文俊在機器證明定理方面取得重大突破，之后又進一步開創了數學機械化領域的新局面。他的機器證明研究采用不同于西方流行的數理邏輯方法，而是通過建立坐標系，將幾何問題代數化，通過方程和多項式理論來解決問題。他說：“我們從事機械化定理證明工作獲得成果之前，對泰斯基的已有工作并無接觸，更沒有想到希爾伯特的《幾何基礎》會與機械化有任何關系。我們是在中國古代數學的啟發之下提出問題并想出解決辦法來的。” 他聲明自己 “關于數學機械化的研究工作，就是在這些思想與成就啟發之下的產物，它是我國自《九章算術》以迄宋元時期數學的直接繼承”。[14]

上述吳文俊在數學史研究基礎上所做的數學機械化研究，說明中國古代數學對現代數學也能提供思想和方法上的借鑒和啟迪。

中國古代數學充分發揮位置的功能，不僅將它用于位值制記數法，而且用它表示未知數及其冪，甚至通過移動個別文字卡片來實現一組運算。特別是四元術，還利用各個方向的不同位置來表示各種的算式。不過，擺放算籌在水平面上只能利用前、后、左、右四個方向標示四個未知量，而在豎直面上擺放算籌就會由于重力的作用難以實現，因此超過四元的籌算操作法有著天然的難度。盡管如此，中國傳統數學中利用多維度上的位置與算籌記數法以及個別的文字卡片相結合，來達到后來運用代數表達式、進行代數運算之效果的方法，展現了具有明顯不同于現代符號代數的中國特征和某些優勢。認真分析這種方法的原理和特征或許可以為現代數學提供啟示。

由于技術條件的限制，中國古代籌算只能利用水平的二維操作面，從而使位置示數法局限于四個未知數之內。現代計算機技術的高度發展，可以模擬三維的空間結構，甚至能夠可視化多維的空間結構。將這種技術結合到中國古代的四元術上，可以很快地將四元拓展到更多元的情形。如果再加以擴展，將中國傳統數學中充分發揮位置作用的思想和方法與現代計算機技術結合起來，或許有可能為現代數學的發展提供新的思路。比如，采用現代的符號表示法與位置示數法表示各種算式，同時將算式置于不同的空間位置表示不同的含義，再根據問題類型的不同性質和條件，設計不同位置上的算式之間的運算法則，從而在發揮位置功能的同時，既能突破四元術由于所利用的維數少而導致未知量個數上的限制，又能充分保留現代符號代數的既有優點。這樣，古老的數學操作方法，可以轉化為現代數學的有效方法，從而為數學研究提供新的發展途徑。當然，這只是一種可能的思路，是不是可行，怎么樣才可行，皆有待今后的探索和驗證。可以肯定的是，具體的應用無疑會存在意想不到的困難，還有待多方努力探索。

中國古代數學內容豐富，思想和方法多樣，本文只是對其中位置示數法的特征做一簡明的闡述，并對其現代意義做初步的探索。更全面的討論，尚需俟諸異日。

致謝中國科學院數學與系統科學研究院魏蕾博士幫助查找資料，謹致謝忱。

注釋

本文系中國科學院戰略研究專項、中國科學院自然科學史研究所 “十四?五” 規劃重大項目 “中國科技傳統及其現實意義研究”（編號：GHJ-ZLZX-2021-17-2）的階段研究成果。
錢寶琮很早就比較系統地提出位置在中國古代數學中的作用，認為中國自古以來記數法就遵從十進位制，用分離系數法表示開方式和方程，是中國古代數學的特征 [2]。其論述具有重要意義，但不是從代數符號發展的視角論述的，而且有些地方也不太準確。
已有學者注意提出中國宋元時期的 “天元術”、“四元術” 在向 “符號化” 方面 “邁出了重要一步”[3]，就功能的相似性而言是可以這樣講的，但這種說法容易忽視中國古代數學方法的特色。因為宋元數學家雖然有 “立天元一為什么”、“立地元一為什么” 等說法相當于現代 “設 $x$ 為什么”、“設 $y$ 為什么”，但在算式中 “天”、“地” 等漢字往往并不出現，而是通過位置來表現它們及其冪，相應的運算方法也有很大不同。

參考文獻

[1] 李文林. 數學史教程（第三版）[M]. 北京：高等教育出版社，2011：127-131.

[2] 錢寶琮. 中國數學史話[M]. 北京: 中國青年出版社，1957: 14-18, 147-150.

[3] 李文林. 中國古代數學的發展及其影響[J]. 中國科學院院刊，2005, 20 (1): 31-36.

[4] 李儼. 籌算制度考[J]. 燕京學報, 1929(6): 1129-1144.

[5] 錢寶琮主編. 中國數學史[M]. 北京: 科學出版社, 1982: 7-9, 51-54, 168-173, 179-186.

[6] 鄒大海. 中國數學的興起與先秦數學[M]. 石家莊: 河北科學技術出版社, 2001: 95-102.

[7] 鄒大海. 中國數學在奠基時期的形態、創造與發展[M]. 廣州: 廣東人民出版社, 2022: 84-93, 102-105, 129-137, 353-357.

[8] Zou Dahai. Whole Number in Ancient Chinese Civilisation：A Survey Based on the System of Counting-units and Expressions[J]. ICMI Study 23: Primary Mathematics Study on Whole Numbers：Proceedings (Edited by Xuhua Sun, Berinderjeet Kaur, Jarmila Novotná), Macao: International Commission in Mathematical Instruction, University of Macau, the Education and Youth Affairs Bureau, Macau SAR, 2015: 157-164.

[9] 郭書春. 九章筭術新校[M]. 合肥: 中國科學技術大學出版社, 2014: 327-328.

[10] Peter Gabriel. Matrizen, Geometrie, Lineare Algebra[M]. Basel; Boston; Berlin: Birk?user, 1996: 19.

[11] 鄒大海. 從出土簡牘文獻看中國早期的正負數概念[J]. 考古學報, 2010 (4): 481-504.

[12] 莫若. 四元玉鑒前序.郭書春主編. 中國科學技術典籍通匯?數學卷一[M]. 鄭州: 河南教育出版社, 1993: 1205.

[13] 祖頤. 四元玉鑒后序. 郭書春主編. 中國科學技術典籍通匯?數學卷一[M]. 鄭州: 河南教育出版社, 1993: 1206.

[14] 吳文俊. 吳文俊論數學機械化[M]. 濟南: 山東教育出版社, 1996: 491, 430-439, 364-365.

【說明】本文刊于《數學通報》2024 年第 12 期第 51 - 56 頁，題為《位置示數法：一種具有代數符號功能的中國傳統數學方法》。
文章原本題為《位置示數法：一種有代數符號功能并具優勢的中國傳統數學方法》，雖嫌稍長，但更能反映本文主旨，故網絡版恢復原標題。文章本來備有摘要，但《數學通報》不需要，現將摘要作為導讀置于正文之前。