一.知識補充

1.什么是樹

如圖是一個現實生活中的樹，觀察可以發現，一棵樹只有一個主干，而主干又會分出許多枝干，這些枝干可能會再分出更多枝干，最后以葉子結束。

樹型結構在現實世界廣泛存在，如人類社會的族譜和各種社會組織機構都可以用樹來形象表示。

數據結構中的樹與現實的樹類似，下圖中的三種都是數據結構中的樹。

樹也是由結點構成的有限集合。我們將樹定義為：
①.有且僅有一個結點被稱為根結點（root）
②.剩余結點又可成為互不相交的集合，每個集合本身是一個樹，也是根結點的子樹。

2.樹的常見概念

根據此圖，為大家介紹一下樹的常見概念。

結點的度：每個結點擁有的子樹個數。

圖中樹的A結點的度為3，B結點的度為2。

葉子結點（終端結點）：度為0的結點，即沒有子樹的結點。

圖中樹的葉子結點有K、L、F、G、M、I、J。

子結點（孩子結點）：a結點是b結點的子樹的根，則a結點是b結點的孩子結點。

圖中樹的B、C、D結點都是A結點的子結點。

雙親結點（父結點）：a結點是b結點的子結點，那么b結點就是a結點的雙親結點。

圖中樹的A結點是B、C、D結點的雙親結點。

兄弟結點：具有相同父節點的結點被稱為兄弟節點。

圖中樹的B、C、D結點即為兄弟結點。

樹的度：一棵樹中所有結點的度中最大的度。

圖中樹的度為3，因為最大的度是A結點和D結點。

結點的層次：從根開始定義，根結點為第一層，根的孩子為第二層，孩子的孩子為第三層，以此類推。（也有的是將根結點定義為第0層，依次相加。）

樹的深度（高度）：結點層次中最大的那個。

圖中樹的深度即為4。

祖先：從根結點到某個結點路徑上的所有結點都是該結點的祖先。

圖中M結點的祖先有H、D、A結點。

子孫：以某結點為根的樹中的所有結點都是它的子孫。

圖中E、F、K、L結點都是B結點的祖孫。

有序樹、無序樹：樹的各個子樹從左至右是有順序的，不能改變，即稱為有序樹，反之為無序樹。

森林：由多棵互不相交的樹構成的集合。

二.二叉樹（Binary Tree）

1.二叉樹的定義

二叉樹是一種特殊的樹，它的特點是每個結點最多只有兩棵子樹，并且子樹的左右順序不能改變。

圖中五種都屬于二叉樹。

2.二叉樹的分類

①.一般二叉樹：

每個結點最多有兩個子結點，無其他要求，結構靈活。

如圖就是一棵普通二叉樹。

②.滿二叉樹：

除了葉子結點，其余所有結點度均為2，不存在度為1的結點。

如圖就是一棵滿二叉樹。

如果一棵滿二叉樹層數為k，那么總結點個數就是2^k - 1(等比數列求和)。

③.完全二叉樹：

對一棵具有n個結點的二叉樹按層序編號，每一個編號為i（1≤i≤n）的結點與同樣深度的滿二叉樹中編號為i 的結點的位置完全相同。

如圖右側就是一棵完全二叉樹。

我們會發現完全二叉樹就像滿二叉樹從最后一個結點開始向左任意刪除n個結點。完全二叉樹最后一層可能不滿，但從左往右結點一定是連續的，因此完全二叉樹只存在一個度為1的結點。
如圖就不是一棵完全二叉樹，因為最后一層葉子結點并非連續的。

滿二叉樹是一種特殊的完全二叉樹。

④.二叉排序樹（二叉查找樹）：

左子樹結點的值均小于根結點，右子樹的值均大于根結點。左右子樹又各是一棵二叉排序樹。

如圖是一棵二叉排序樹。

二叉排序樹常用于元素的搜索和排序。

⑤.平衡二叉樹：

平衡二叉樹上任意一個結點的左右子樹的高度差不會超過1。

如圖就是一棵平衡二叉樹。

平衡二叉樹與二叉查找樹相結合可以提高搜索效率。

⑥.其他二叉樹：
線索二叉樹（Threaded Binary Tree）：通過空指針指向先驅或后繼節點，優化遍歷。
哈夫曼樹（Huffman Tree）：用于數據壓縮，按頻率構建的帶權二叉樹。等等

3.二叉樹的性質

①.一棵二叉樹的第i層上，最多有2^i-1個結點。
②.一棵二叉樹如果總共有k層，那么它最多有2^k-1個結點。
③.一棵二叉樹如果其度為0的結點個數為n0，度為2的結點個數為n2，那么滿足n0=n2+1。

三.二叉樹的實現

在邏輯上，樹是用遞歸定義的，而二叉樹的各種操作也是使用遞歸實現的，因此對遞歸還不熟悉的朋友建議先學習一下遞歸，否則可能較難上手。

1.二叉樹的存儲

我們在實現數據元素的存儲時，應當明確的是，對于樹來說，它的存儲應當著重關注數據元素以及數據元素之間的邏輯關系在存儲器中的表示。說人話就是，如何表示樹的結點之間的邏輯關系，即如何表示結點的雙親和孩子。
二叉樹的存儲也有順序存儲和鏈式存儲兩種。（樹的存儲結構常用鏈表結構）

順序存儲：
一棵二叉樹的順序存儲就是用一組地址連續的存儲單元依次自上而下、自左至右存儲樹上的結點。

如圖是一棵完全二叉樹

如上所示，這棵樹的結點的編號就是按照從上到下、從左到右來編號。在數組中存儲時，就是按照下面這樣的方式來去順序存儲：(數組中的內容是相應編號的結點數據)。

借著完全二叉樹，我們可以理解一般二叉樹的順序存儲。
如圖是一棵普通二叉樹

我們在進行存儲時先將它補全：

那么在數組中的就是這樣存儲的：

這種存儲方式有較明顯的缺點，如圖是一棵很不平衡的二叉樹：

它僅有四個結點，但在數組中存儲時卻浪費了較大空間。

鏈式存儲：
因為二叉樹最多有兩個孩子結點，只有一個雙親結點，因此在定義鏈式存儲時有兩種表示：二叉鏈、三叉鏈。

二叉鏈：有兩個指針域，一個指向左孩子，另一個指向右孩子。

其結構表示為：

typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* leftchild;struct BinaryTreeNode* rightchild;
}BTNode;

三叉鏈：有三個指針域，一個指向雙親結點，另外兩個指向左、右孩子結點。

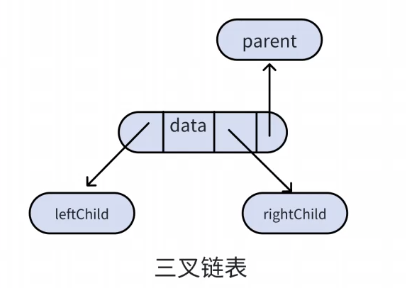
其結構表示為;

typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* leftchild;struct BinaryTreeNode* rightchild;struct BinaryTreeNode* parent;
}BTNode;

普通二叉樹一般用二叉鏈結構表示，特殊二叉樹（AVL樹、紅黑樹、B樹等）會采用三叉鏈結構來表示。

本文使用二叉鏈式結構來實現二叉樹。由于二叉樹是由根結點，左子樹，右子樹構成，其中左子樹也包含它的根結點，左子樹和右子樹。

2.二叉樹的遍歷

二叉樹的遍歷是指從根結點出發按照某種次序依次訪
問二叉樹中的所有結點，使得每個結點被訪問一次且僅被訪問一次。

對于線性結構，遍歷是很簡單的事。一個數組我們可以從頭到尾依次遍歷，一個鏈表我們可以根據結點的指向來遍歷，那么對于一個有多分支的樹形結構，我們如何遍歷一棵二叉樹呢？可以通過以下四種方法。

①.先序遍歷

先序遍歷也叫前序遍歷，就是根結點在前，按照根->左->右的順序遞歸遍歷一棵樹。
若二叉樹為空，則返回；否則：①訪問根結點；②前序遍歷根結點的左子樹；③前序遍歷根結點的右子樹。

由于每個結點又包含左子樹和右子樹，因此遍歷完該結點，遍歷它的左子樹時，同樣要進入左子樹的左子樹，按照根->左->右的順序遍歷，直到最底層的結點的左右子樹都遍歷完，再向上返回遍歷其他結點。
以圖中這棵樹為例，詳細講解一下先序遍歷的過程。

先序遍歷這棵樹，先訪問根結點，得到A，然后遍歷A的左子樹：
對于該左子樹，同樣先訪問根結點，得到A->B，再遍歷B的左子樹

同樣先訪問根結點，得到A->B->D，再遍歷D的左子樹，左子樹為空，然后遍歷D的右子樹，得到A->B->D->G。
B這棵左子樹遞歸遍歷完之后依次向上返回，進入A的右子樹。

同樣先訪問根結點，得到A->B->D->G->C，進入C的左子樹

同樣先訪問根結點，得到A->B->D->G->C->E，然后遍歷左子樹，為空，再遍歷右子樹，為空，返回。
C的左子樹遍歷完，進入C的右子樹

同樣先訪問根結點，得到A->B->D->G->C->E->F，然后遍歷左子樹，為空，再遍歷右子樹，為空，返回。

至此，整棵樹已經完全被遍歷完，順序如圖

得到先序遍歷結果是：A->B->D->G->C->E->F。

代碼實現為：

//先序遍歷
void PreOrder(BTNode* root)
{//根結點為空，即樹為空時，直接返回if (root == NULL)return;printf("%c ", root->data);  //遍歷根結點PreOrder(root->leftchild);  //遍歷左子樹PreOrder(root->rightchild); //遍歷右子樹}

②.中序遍歷

中序遍歷即根結點在中間，按照左->根->右的順序遞歸遍歷一棵樹，即：①中序遍歷根結點的左子樹；②訪問根結點；③中序遍歷根結點的右子樹。

每個結點都包含左子樹和右子樹。在遍歷時從根結點進入它的左子樹，再進入左子樹的左子樹，直到進入最后一個左子樹，訪問該左子樹的左孩子，然后訪問根結點，然后訪問右孩子，再依次向上返回遍歷剩下結點。
依舊按照這棵樹為例，詳細講述中序遍歷的過程。

中序遍歷這棵樹，首先根據根結點進入A的左子樹：

B的左子樹不為空，再進入B的左子樹：

發現D的左子樹為空，返回，然后訪問根結點得到D，然后進入D的右子樹：

發現G的左子樹為空，返回，訪問根結點得到D->G，G的右子樹也為空，返回。
此時B的左子樹遍歷完，訪問B這個結點，得到D->G->B，
然后進入B的右子樹，為空，返回。
A的左子樹已經全部遍歷完，訪問A這個結點，得到D->G->B->A，然后進入A的右子樹：

C的左子樹不為空，進入C的左子樹：

發現E的左子樹為空，返回，然后訪問B結點，得到D->G->B->A->E，E的右子樹也為空，返回。
C的左子樹遍歷完，訪問C結點，得到D->G->B->A->E->C，然后進入C的右子樹：
F的左子樹為空，返回，訪問F結點得到D->G->B->A->E->C->F，F的右子樹為空，返回。
此時C這棵樹已經全部遍歷完，向上返回，A這棵樹也全部遍歷完，中序遍歷結束，順序為：

遍歷結果為D->G->B->A->E->C->F。

代碼實現為：

//中序遍歷
void InOrder(BTNode* root)
{if (root == NULL)return;InOrder(root->leftchild);//先遍歷左子樹printf("%c ", root->data);//然后是根InOrder(root->rightchild);//最后是右子樹
}

③.后序遍歷

后序遍歷即按照左->右->根的順序，最后訪問根結點的操作，即：①后序遍歷根結點左子樹；②后序遍歷根結點的右子樹；③最后訪問根結點。

依舊以該樹為例進行后序遍歷，這次畫圖演示，不做詳細說明。


得到的后序遍歷結果為：G->D->B->E->F->C->A。
代碼實現為：

//后序遍歷
void PostOrder(BTNode* root)
{if (root == NULL)return;PostOrder(root->leftchild); //先遍歷左子樹PostOrder(root->rightchild);//再遍歷右子樹printf("%c ", root->data);  //最后遍歷根結點
}

④.層序遍歷

層序遍歷即一層一層地依次訪問每個結點。

如圖即為層序遍歷的順序：

層序遍歷是借助隊列這個數據結構來實現的（對隊列不清楚的可以先看看我這篇講述隊列的博客鏈接: 【數據結構】–隊列。）

首先將根結點加入隊列，當隊列不為空時，取出隊頭結點，訪問該結點，然后將隊頭結點的左孩子，右孩子加入隊列。循環執行該操作，直到隊列所有元素都取出，隊列為空時停止。
代碼實現為：

//層序遍歷
void LevelOrder(BTNode* root)
{//借助隊列完成Queue q;QueueInit(&q);if (root == NULL)return;QueuePush(&q, root);while (QueueSize(&q)){BTNode* tmp = QueueFront(&q);QueuePop(&q);if (tmp->leftchild)QueuePush(&q, tmp->leftchild);if (tmp->rightchild)QueuePush(&q, tmp->rightchild);printf("%c ", tmp->data);}
}

OK，這篇文章先講到這里，二叉樹內容有點多且相對較難，剩下的操作下篇文章再詳細介紹。
感謝閱讀！^ _ ^