一、什么是奇異值

?二、核心思想：

三、奇異值的主要應用

1、降維：

2、數據壓縮：

原理：圖像可以表示為一個矩陣，矩陣的元素對應圖像的像素值。對這個圖像矩陣進行 SVD 分解后，小的奇異值對圖像的主要結構貢獻很小，它們往往對應于圖像中的細節和噪聲。通過丟棄這些小的奇異值，只保留較大的奇異值及其對應的列向量，再用保留的部分重建圖像矩陣，就可以在盡量保持圖像主要內容的同時，大幅減少存儲圖像所需的數據量。

3、去噪：

在很多實際數據中，噪聲往往表現為在各個方向上的微小干擾，反映在奇異值上就是一些較小的奇異值。通過丟棄這些小的奇異值及其對應的奇異向量，然后用剩下的較大奇異值部分重建數據矩陣，就可以有效地去除噪聲，提高數據的質量。

4、推薦系統：

在推薦系統中，用戶-物品評分矩陣通常存在很多缺失值，對評分矩陣R進行SVD分解后，保留前k個較大的奇異值及其對應的U、V的部分列向量，構建低秩矩陣來近似R。這樣就可以利用已知的評分來預測缺失的評分值，從而為用戶推薦可能感興趣的內容。

四、矩陣代碼實例

import numpy as np# 創建一個矩陣 A (5x3)
A = np.array([[1, 2, 3],[4, 5, 6],[7, 8, 9],[10, 11, 12],[13, 14, 15]])
print("原始矩陣 A:")
print(A)# 進行 SVD 分解
# full_matrices=False表示不計算完整的 U 和 V 矩陣，而是計算經濟規模的分解，用于降維場景
U, sigma, Vt = np.linalg.svd(A, full_matrices=False)
print("\n奇異值 sigma:")
print(sigma)# 分別保留前 k 個奇異值進行降維
for k in [1, 2, 3]:U_k = U[:, :k] # 取 U 的前 k 列，因為要保持行數不變sigma_k = sigma[:k] # 取前 k 個奇異值Vt_k = Vt[:k, :] # 取 Vt 的前 k 行，因為要保持列數不變# 近似重構矩陣 A,p.diag() 將 sigma_k 轉換為對角矩陣。@ 運算符表示矩陣乘法。A_approx = U_k @ np.diag(sigma_k) @ Vt_k# 近似誤差等于差異程度的弗羅貝尼烏斯范數（fro 值）占原始矩陣fro值的比例。error = np.linalg.norm(A - A_approx, 'fro') / np.linalg.norm(A, 'fro')print(f"k={k} 時的近似誤差: {error:.6f}")

k=1 時：原始3維列空間降為1維，使用U的第1列和Vt的第1行，結合第一個奇異值，重新擬合原矩陣，近似誤差僅為4.19%。

k=2 時：原始3維列空間降為2維，使用U的前2列Vt的前2行，結合前兩個奇異值，重新擬合原矩陣，此時已完全重構原始矩陣（誤差為0）。

k=3 時：使用全部3個左/右奇異向量，但第三個奇異值為0，沒有額外價值。

想象一個三維數據點云，SVD 分解會找到三個正交方向：

• 第一個方向（對應最大奇異值）：數據方差最大的方向，即數據點最 “伸展” 的方向。
• 第二個方向（次大奇異值）：與第一個方向正交且方差次大的方向。
• 第三個方向（最小奇異值）：與前兩個方向正交且方差最小的方向。

當用?k=1?降維時，相當于將數據投影到第一個方向上，保留最主要的特征。如果選擇第三個方向（最小奇異值），則會丟失所有重要信息。

五、機器學習代碼實例

1、如何確保測試集和訓練集降維到同?k 個特征空間？

訓練集和測試集需經過相同變換來保證數據分布一致，這是確保模型評估和泛化有效性的關鍵。

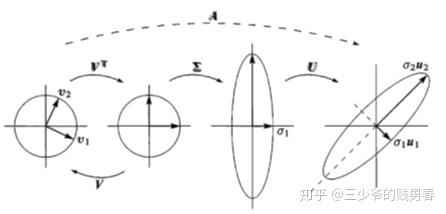
?任何線性變換（如矩陣乘法）都可以分解為旋轉 → 縮放 → 再旋轉三個步驟。?

為什么使用右奇異向量而不是左奇異向量？?

2、代碼實例

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score# 設置隨機種子以便結果可重復
np.random.seed(42)# 模擬數據：1000 個樣本，50 個特征
n_samples = 1000
n_features = 50
# 隨機生成特征數據，并改變數據尺度，使范圍大致在均值 0 附近，標準差變為 10
X = np.random.randn(n_samples, n_features) * 10 
y = (X[:, 0] + X[:, 1] > 0).astype(int)  # 模擬二分類標簽# 劃分訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
print(f"訓練集形狀: {X_train.shape}")
print(f"測試集形狀: {X_test.shape}")# 對訓練集進行 SVD 分解
U_train, sigma_train, Vt_train = np.linalg.svd(X_train, full_matrices=False)
print(f"Vt_train 矩陣形狀: {Vt_train.shape}")# 選擇保留的奇異值數量 k
k = 10
Vt_k = Vt_train[:k, :]  # 保留前 k 行，形狀為 (k, 50)
print(f"保留 k={k} 后的 Vt_k 矩陣形狀: {Vt_k.shape}")# 降維訓練集：X_train_reduced = X_train @ Vt_k.T
X_train_reduced = X_train @ Vt_k.T
print(f"降維后訓練集形狀: {X_train_reduced.shape}")# 使用相同的 Vt_k 對測試集進行降維：X_test_reduced = X_test @ Vt_k.T
X_test_reduced = X_test @ Vt_k.T
print(f"降維后測試集形狀: {X_test_reduced.shape}")# 訓練模型（以邏輯回歸為例）
model = LogisticRegression(random_state=42)
model.fit(X_train_reduced, y_train)# 預測并評估
y_pred = model.predict(X_test_reduced)
accuracy = accuracy_score(y_test, y_pred)
print(f"測試集準確率: {accuracy}")# 計算訓練集的近似誤差（可選，僅用于評估降維效果）
X_train_approx = U_train[:, :k] @ np.diag(sigma_train[:k]) @ Vt_k
error = np.linalg.norm(X_train - X_train_approx, 'fro') / np.linalg.norm(X_train, 'fro')
print(f"訓練集近似誤差 (Frobenius 范數相對誤差): {error}")

六、注意的問題?

1、標準化數據

不同特征可能具有不同的量綱（比如一個特征表示年齡，范圍可能是 0 - 100，另一個特征表示收入，可能是 0 - 1000000），如果不進行標準化，具有較大數值范圍的特征可能會在 SVD 計算中占據主導地位，從而影響降維結果。

標準化可以將所有特征轉化到相同的尺度，使得每個特征對降維的貢獻更加公平。可以使用 sklearn.preprocessing.StandardScaler。

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

對測試集?X_test調用transform方法，使用在訓練集上計算得到的均值和方差對測試集數據進行標準化。不能在測試集上使用fit_transform，否則會導致數據泄漏，會使模型評估結果過于樂觀。?

2、選擇合適的 k

可以通過累計方差貢獻率（explained variance ratio）選擇 k ，通常選擇解釋 90%-95% 方差的 k ?值，它可以幫助我們確定保留多少個奇異值能夠解釋大部分的數據方差。

# 表示前k個奇異值所解釋的方差（奇異值平方的累積和）占總方差的比例。
explained_variance_ratio = np.cumsum(sigma_train**2) / np.sum(sigma_train**2)
print(f"前 {k} 個奇異值的累計方差貢獻率: {explained_variance_ratio[k-1]}")

3、使用 sklearn 的 TruncatedSVD

對于大規模數據，完整的 SVD 計算可能非常耗時且占用大量內存。TruncatedSVD類專門用于高效降維，它直接計算前k個奇異值和向量，避免了完整 SVD 的計算開銷，提高了計算效率。

from sklearn.decomposition import TruncatedSVD
svd = TruncatedSVD(n_components=k, random_state=42)
X_train_reduced = svd.fit_transform(X_train)
X_test_reduced = svd.transform(X_test)
print(f"累計方差貢獻率: {sum(svd.explained_variance_ratio_)}")

@浙大疏錦行?