1. LC56 合并區間

題目鏈接

1. Arrays.sort先讓intervals里的子數組按照子數組的第一個數字值從小到大排列。
2. 開一個新數組，newInterval，存放合并好的子數組
3. 讓intervals的當前子數組i的第一個數字與newInterval的當前子數組index的最后一個數字比較大小：如果區間沒有重疊，則interval的i加入newInterval; 如果重疊，則與newInterval的區間合并
4. 注意合并時，并不是newInterval[index][1] = intervals[i][1]；
   而是newInterval[index][1] = Math.max(newInterval[index][1], intervals[i][1]);
   因為有可能是這種情況：[1,6],[2,4]——這種情況合并還是[1,6]。
   

秒懂力扣區間題目：重疊區間、合并區間、插入區間

class Solution {public int[][] merge(int[][] intervals) {Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]);int[][] newInterval = new int[intervals.length][2];newInterval[0] = intervals[0];int index = 0;for (int i=1; i<intervals.length; i++){if (intervals[i][0] > newInterval[index][1]){index++;newInterval[index] = intervals[i];}else{newInterval[index][1] = Math.max(newInterval[index][1], intervals[i][1]);}}return Arrays.copyOf(newInterval, index+1);}
}

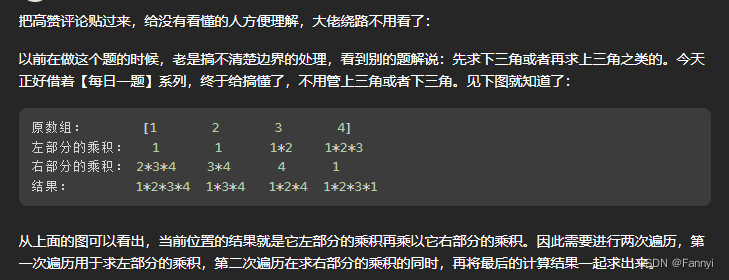
2. LC238除自身以外數組的乘積

題目鏈接

class Solution {public int[] productExceptSelf(int[] nums) {int[] left = new int[nums.length];int[] right = new int[nums.length];//leftleft[0] = 1;for (int i=1; i<left.length; i++){left[i] = left[i-1] * nums[i-1];}//rightright[right.length-1] = 1;for (int i=right.length-2; i>=0; i--){right[i] = right[i+1] * nums[i+1];}//合并int[] result = new int[nums.length];for (int i=0; i<nums.length; i++){result[i] = left[i] * right[i];}return result;}
}

3.隨想錄1、二分查找

題目鏈接

最重要的是確定左閉右閉區間，所以while條件是<=。因為左閉右閉就是左邊區間也包括，右邊區間也包括，所以左右區間可以=。如果是開區間，一個區間不包括，一個區間包括，那么兩個區間必不能相等。

代碼

class Solution {public int search(int[] nums, int target) {int left = 0;int right = nums.length-1;// 避免當 target 小于nums[0] nums[nums.length - 1]時多次循環運算if (target < nums[0] || target > nums[nums.length - 1]) {return -1;}while(left <= right){int mid = (right+left)/2;if (nums[mid] == target){return mid;}else if (nums[mid] > target){right = mid - 1;}else if (nums[mid] < target){left = mid + 1;}}return -1;}
}

4. LC560 和為k的子數組

題目鏈接

解法一：
暴力算法
易錯：在外層循環時，nums[i] == k了之后不要continue，還有繼續內循環。因為可能會有這種情況：滿足和為k之后，后面出現了1和-1。此時相加和依然為k。

class Solution {public int subarraySum(int[] nums, int k) {int sum = 0;int count = 0;for (int i=0; i<nums.length; i++){sum = nums[i];if (nums[i] == k){count++;}for (int j=i+1; j<nums.length; j++){sum += nums[j];if (sum == k){count++;}}}return count;}
}

解法二：
前綴和

假設數組的前綴和數組為prefixSum，其中prefixSum[i]表示從數組起始位置到第i個位置的元素之和。

對于任意的兩個下標i和j（i < j），如果prefixSum[j] - prefixSum[i] = k，即從第i個位置到第j個位置的元素之和等于k，那么說明從第i+1個位置到第j個位置的連續子數組的和為k。

遍歷數組，計算每個位置的前綴和，并使用一個哈希表來存儲每個前綴和出現的次數。在遍歷的過程中，檢查是否存在prefixSum[j] - k的前綴和，如果存在，說明從某個位置到當前位置的連續子數組的和為k，將對應的次數累加到結果中。

這樣，通過遍歷一次數組，統計出和為k的連續子數組的個數，并且時間復雜度為O(n)，其中n為數組的長度。

class Solution {public int subarraySum(int[] nums, int k) {int preSum = 0;int count = 0;Map<Integer, Integer> map = new HashMap<>();map.put(0,1); // 初始化前綴和為0的次數為1for (int i=0; i<nums.length; i++){preSum += nums[i];if (map.containsKey(preSum-k)){count += map.get(preSum-k);}if (map.containsKey(preSum)){map.put(preSum, map.get(preSum)+1);}else{map.put(preSum, 1);}}return count;}
}

！！為什么要初始化前綴和？
如果從數組的開始位置到當前位置的子數組的和恰好等于 k，那么這個子數組的前綴和就是 0，即 sum - k 等于 0。因此，需要初始化一個前綴和為 0 的次數為 1，表示從數組的開始位置到當前位置的子數組的和為 k 的情況。如果不初始化，那么這種情況會被漏掉，導致結果不正確。