[動態規劃]---part1

前言

作者：小蝸牛向前沖

專欄：小蝸牛算法之路

?專欄介紹："蝸牛之道，攀登大廠高峰，讓我們攜手學習算法。在這個專欄中，將涵蓋動態規劃、貪心算法、回溯等高階技巧，不定期為你奉上基礎數據結構的精彩算法之旅。一同努力，追逐技術的星辰大海。"

?

目錄

?一、什么是動態規劃

1、什么是動態規劃

2、動態規劃的學習

二、動態規劃刷題

1、第 N 個泰波那契數

a、解題思路：

b、代碼?

2、? ?面試題 08.01. 三步問題

?a、解題思路：

b、代碼

3 、746. 使用最小花費爬樓梯

a、解題思路?

b、代碼

? 4、解碼方法

a、解題思路?

b、代碼

c、代碼優化?

?5、不同路徑（medium）

a、解題思路?

b、代碼

本期我們將探討動態規劃，并提供5道經典動態規劃問題，難度由淺入深。

?一、什么是動態規劃

1、什么是動態規劃

在學習算法的過程中，我們往往會遇到一些算法題是要用動態規劃來解決。

但是做為小白的我們哪里知道動態規劃是什么？

從概念上說

動態規劃（Dynamic Programming）是一種解決復雜問題的算法設計技術。它通常用于解決具有重疊子問題和最優子結構性質的問題，通過將問題分解為更小的子問題，并利用子問題的解來構建原始問題的解。

看完概念我們知道什么是動態規劃，求重疊類子問題的?一般會用到動態規劃的思路。

那我們如何求學習動態規劃

2、動態規劃的學習

對于算法類題目，在我們掌握算法的基本原理后，就是進行大量刷題，進經驗的總結。

求解動態規劃的五步驟：

1、狀態表示

?在求解過程中，我們往往要創建dp表(其實就是數組），狀態表示就是我們要找出dp表中值的含義是什么。

狀態表?怎么來？

  • 根據題目要求
  • 經驗+題目要求
  • 分析題目的過程中，發現重復子問題

?2、狀態轉移方程

?簡單說是和dp[i]有關的一個方程

?3、初始化

保證在填寫dp表的時候不越界

4、填寫順序?

?根據前面的計算得來，可以從前往后，也可以從后往前。

?5、返回值

根據題目要求+狀態表示

?講完了解題步驟，下面就進行刷題訓練。

特別提醒：后面博客會帶領大家由易到難進行刷題，每期都為五題。

二、動態規劃刷題

1、第 N 個泰波那契數

泰波那契序列?Tn?定義如下：?

T0?= 0, T1?= 1, T2?= 1, 且在 n >= 0?的條件下 Tn+3?= Tn?+ Tn+1?+ Tn+2

給你整數?n，請返回第 n 個泰波那契數?Tn?的值。

示例 1：

輸入：n = 4
輸出：4
解釋：
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4

示例 2：

輸入：n = 25
輸出：1389537

提示：

  • 0 <= n <= 37
  • 答案保證是一個 32 位整數，即?answer <= 2^31 - 1。

a、解題思路：

1、題目中的狀態表示是什么？

?dp[i] 表?：第 i 個泰波那契數的值。

2、狀態轉移方程

由題目意很很容易知道是T(n) = T(n-1)+T(n-2)+T(n-3)

3、初始化dp表

為了防止數組越界我們只需要初始化:

dp[0]=0;

dp[1]=1;

dp[2]=1;

4、?填表順序

由狀態方程+題意知道從左往右填寫到N

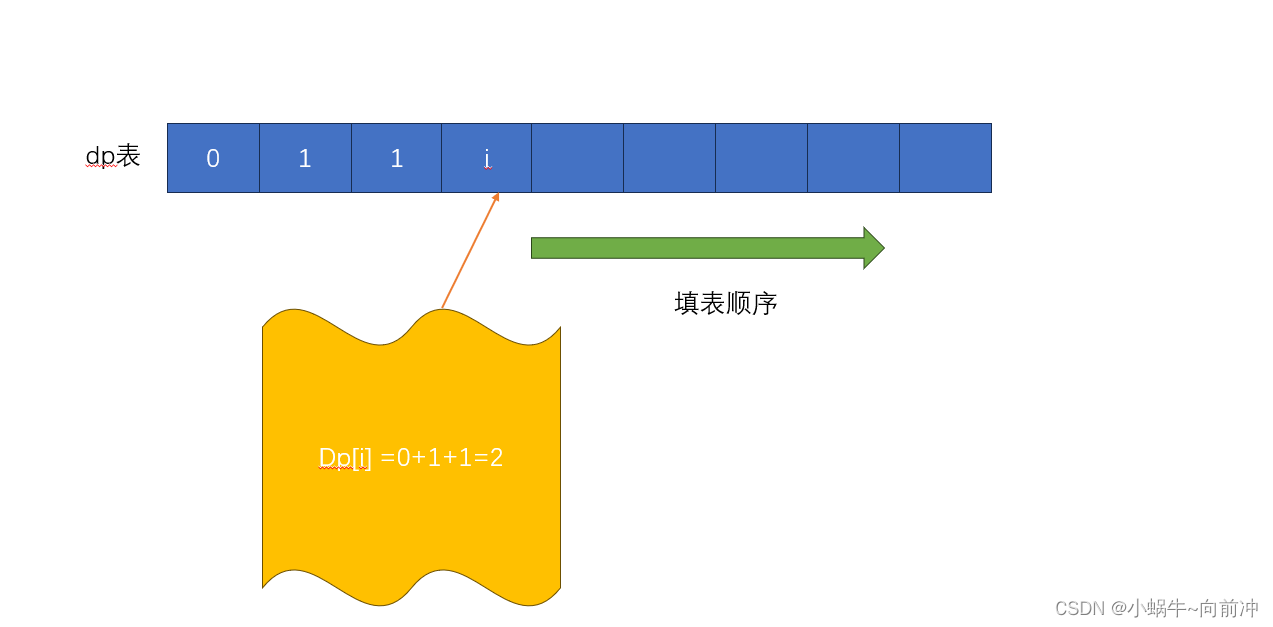
5、返回值

根據題目要求和dp[i]就為dp[n]

b、代碼?

class Solution {
public:int tribonacci(int n) {//動態規劃//1.創建dp表//2.初始化表//3.填表//4.返回值//處理邊界情況if(n==0)return 0;if(n==1||n==2)return 1;//1、創建dp表vector<int> dp(n+1);//2、初始化表dp[0]=0,dp[1]=1,dp[2]=1;//3、填表for(int i = 3;i<=n;i++){dp[i] = dp[i-1]+dp[i-2]+dp[i-3];}//4、返回return dp[n];}
};

Leetcode 測試結果：?

2、? ?面試題 08.01. 三步問題

三步問題。有個小孩正在上樓梯，樓梯有n階臺階，小孩一次可以上1階、2階或3階。實現一種方法，計算小孩有多少種上樓梯的方式。結果可能很大，你需要對結果模1000000007。

示例1:

 輸入：n = 3 
 輸出：4
 說明: 有四種走法

示例2:

 輸入：n = 5
 輸出：13

提示:

  1. n范圍在[1, 1000000]之間

?a、解題思路：

從0位置開始跳，下面我們來思考一下題意：

?----->（表示跳臺階）

n=1時候

從0----->1?

走法為1

n=2時候

從0----->2

或者說我們讓1----->2因為從?0----->1的走法我們已經考慮過了

走法為2

n=3時候

從0----->3或者說

我們讓1----->3因為從?0----->1的走法我們已經考慮過了走法為1

也可以2----->3因為從?0----->2的走法我們已經考慮過了走法為2

走法為1+1+2=4

n=4時候

不管怎么說先走到1，在從1----->4走法為1

不管怎么說先走到2，在從2----->4走法為2

不管怎么說先走到3，在從3----->4走法為4

總共走法：1+2+4=7

大家這里是不是已經思路清晰起來了?

1、轉態表示

以i位置為結尾，正好是到達第N個臺階，所以我們認為：

dp[i]表示：到達i位置時，一共有多少方法。

?2、狀態轉移方程

以i位置的狀態，最近進的一步進行劃分

從(i-1)--->i? ?dp[i-1]種走法

從(i-2)--->i? ?dp[i-2]種走法

從(i-3)--->i? ?dp[i-3]種走法

所以狀態方程為：dp[i]=dp[i-1]+dp[i-2]+dp[i-3]?;

3、初始化

這里我們注意我們用不到i==0,因為0臺階的研究沒有意義。

? dp[1] = 1, dp[2] = 2, dp[3] = 4;

4、?填表順序

根據前面的推斷肯定是從左往右。

5、返回值

根據題目要求和dp[i]就為dp[n]

b、代碼

這題雖然和第一題非常相似但是有細節要處理、

class Solution {
public://取模const int MOD = 1e9 + 7;int waysToStep(int n){//處理邊界情況：if (n == 1 || n == 2)return n;if (n == 3)return 4;//創建dp表vector<int> dp(n + 1);//初始化dp[1] = 1, dp[2] = 2, dp[3] = 4;//填表for (int i = 4; i <= n; i++){//結果可能很大要進去取模dp[i] = ((dp[i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;}//返回return dp[n];}
};

Leetcode 測試結果：?

3 、746. 使用最小花費爬樓梯

給你一個整數數組?cost?，其中?cost[i]?是從樓梯第?i?個臺階向上爬需要支付的費用。一旦你支付此費用，即可選擇向上爬一個或者兩個臺階。

你可以選擇從下標為?0?或下標為?1?的臺階開始爬樓梯。

請你計算并返回達到樓梯頂部的最低花費。

示例 1：

輸入：cost = [10,15,20]
輸出：15
解釋：你將從下標為 1 的臺階開始。
- 支付 15 ，向上爬兩個臺階，到達樓梯頂部。
總花費為 15 。

示例 2：

輸入：cost = [1,100,1,1,1,100,1,1,100,1]
輸出：6
解釋：你將從下標為 0 的臺階開始。
- 支付 1 ，向上爬兩個臺階，到達下標為 2 的臺階。
- 支付 1 ，向上爬兩個臺階，到達下標為 4 的臺階。
- 支付 1 ，向上爬兩個臺階，到達下標為 6 的臺階。
- 支付 1 ，向上爬一個臺階，到達下標為 7 的臺階。
- 支付 1 ，向上爬兩個臺階，到達下標為 9 的臺階。
- 支付 1 ，向上爬一個臺階，到達樓梯頂部。
總花費為 6 。

提示：

  • 2 <= cost.length <= 1000
  • 0 <= cost[i] <= 999

a、解題思路?

這里我們要注意到達樓頂，應該是const數組最后一個位置的下一個位置

這里我們有二種思路：

思路一：

1、轉態表示

以i位置為結尾，正好是樓頂，所以我們認為：

dp[i]表示：到達i位置時，最小花費

?2、狀態轉移方程

根據最近的一個位置劃分

先到達i-1的位置，然后支付const[i-1],走一步，?花費：dp[i-1]+cost[i-1]

先到達i-2的位置，然后支付const[i-2],走一步，?花費：dp[i-2]+cost[i-2]

所以dp[i] =min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);

3、初始化

保證dp表不越界就好dp[0]=dp[1]=0;

4、?填表順序

從左往右

5、返回值

dp[n]

思路2：

1、轉態表示

以i位置為起點，到達樓頂，所以我們認為：

dp[i]表示：從i位置出發到達樓頂，此時最小花費

?2、狀態轉移方程

根據最近的一個位置劃分

  • 支付const[i],往后走一步，?從i+1位置出發到樓頂，花費：dp[i+1]+cost[i]
  • 支付const[i],往后走二步，?從i+2位置出發到樓頂，花費：dp[i+2]+cost[i]

所以dp[i] =min(dp[i+1]+cost[i],dp[i+2]+cost[i]);

3、初始化

保證dp表不越界就好dp[n-1]=cost[n-1],dp[n-2]=cost[n-2];

4、?填表順序

從右往左

5、返回值

min(dp[0],dp[1]);

b、代碼

這里有二種解題思路：

思路一：

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {//處理邊界情況int n = cost.size();if(n==0||n==1)return cost[n];//創建dp表vector<int> dp(n+1);//填表for(int i = 2;i<=n;i++){dp[i] =min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}//返回return dp[n];}
};

?Leetcode 測試結果：?

?解法二：

class Solution {
public:int minCostClimbingStairs(vector<int>& cost){int n = cost.size();//創建dp表vector<int> dp(n+1);//初始化dp[n-1]=cost[n-1],dp[n-2]=cost[n-2];//填表for(int i = n-3;i>=0;i--){dp[i] = min(dp[i+1]+cost[i],dp[i+2]+cost[i]);}//返回return min(dp[0],dp[1]);}
};

?Leetcode 測試結果：??

? 4、解碼方法

一條包含字母?A-Z?的消息通過以下映射進行了?編碼?：

'A' -> "1"
'B' -> "2"
...
'Z' -> "26"

要?解碼?已編碼的消息，所有數字必須基于上述映射的方法，反向映射回字母（可能有多種方法）。例如，"11106"?可以映射為：

  • "AAJF"?，將消息分組為?(1 1 10 6)
  • "KJF"?，將消息分組為?(11 10 6)

注意，消息不能分組為??(1 11 06)?，因為?"06"?不能映射為?"F"?，這是由于?"6"?和?"06"?在映射中并不等價。

給你一個只含數字的?非空?字符串?s?，請計算并返回?解碼?方法的?總數?。

題目數據保證答案肯定是一個?32 位?的整數。

?

示例 1：

輸入：s = "12"
輸出：2
解釋：它可以解碼為 "AB"（1 2）或者 "L"（12）。

示例 2：

輸入：s = "226"
輸出：3
解釋：它可以解碼為 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。

示例 3：

輸入：s = "06"
輸出：0
解釋："06" 無法映射到 "F" ，因為存在前導零（"6" 和 "06" 并不等價）。

提示：

  • 1 <= s.length <= 100
  • s?只包含數字，并且可能包含前導零。

a、解題思路?

看我們題目后，根據經驗此題位動態規劃解題

1、轉態表示

首先我們想以i位置為結尾表示什么

dp[i]表示：以i位置結尾的時候，解碼的方法有多少種

?2、狀態轉移方程

根據最近的一個位置劃分

讓s[i]單獨解碼的時候,假設a=s[i]

  • 成功,a!='0'（或者說是a>='1'&&a<='9'），解碼的種類有dp[i-1]種
  • 失敗為0

讓s[i-1]和s[i]組合進行解碼?假設組合為b

  • 成功b>='10'&&b<='26',解碼的種類有dp[i-2]種
  • 失敗為0

有同學可能會想為什么不讓dp[i]和dp[i+1]進行組合，但是大家?要明白，填表到dp[i]的時候，我們是知道dp[i-1]有多少種解碼，但是我們不知道dp[i+1]有多少種解碼。

所以狀態轉移方法為

單獨解碼

dp[i] +=dp[i-1];

組合解碼

dp[i]=dp[i-2];

3、初始化

保證dp表

dp[0] = s[0]!='0';if(s[0]!='0'&&s[1]!='0') dp[1] +=dp[0];//這里我們還要把組合轉換為數字進行判斷int t = (s[0]-'0')*10+(s[1]-'0');if(t>=10&&t<=26) dp[1] +=1;

4、?填表順序

從左往右

5、返回值

dp[n-1]

b、代碼

class Solution {
public:int numDecodings(string s){//創建dp表int n = s.size();vector<int> dp(n);//初始化dp[0] = s[0]!='0';//處理邊界情況if(n==1) return dp[0];//單解碼if(s[0]!='0'&&s[1]!='0') dp[1] +=dp[0];//組合起來int t = (s[0]-'0')*10+(s[1]-'0');if(t>=10&&t<=26) dp[1] +=1;//填表for(int i = 2;i<n;i++){//單解碼if(s[i]!='0') dp[i] +=dp[i-1];//雙解碼int t = (s[i-1]-'0')*10+(s[i]-'0');if(t>=10&&t<=26) dp[i] +=dp[i-2];}//返回return dp[n-1];}
};

?Leetcode 測試結果：?

c、代碼優化?

不知道大家分發現沒，我們在初始化的代碼和填表的代碼，有著非常相似的特色，那我們能不能進行優化呢？

其實是可以的，多一個數組的空間就可以了。

簡單的理解就是，把初始化的過程和填表合并了。但要注意二個問題：

那個虛擬節點dp[0]填寫多少？后面大家做都了這種題，很多情況下都是填寫0但，但是這里卻是填寫dp[0]=1;?

為什么了，因為我們這里要保證后面填寫的正確

比如：在進雙解碼的時候dp[i]+=dp[i-2]，如何i=2時候，這里我們吧dp[0]初始化為0就會漏掉這種情況。

下標映射關系如上圖。

class Solution {
public:int numDecodings(string s){//創建dp表int n = s.size();vector<int> dp(n+1);//初始化dp[0] = 1;//保證后面的填表的正確性//處理邊界情況dp[1] = s[1-1]!='0';if(n==1) return dp[1];//填表for(int i = 2;i<=n;i++){//單解碼if(s[i-1]!='0') dp[i] +=dp[i-1];//雙解碼int t = (s[i-2]-'0')*10+(s[i-1]-'0');if(t>=10&&t<=26) dp[i] +=dp[i-2];}//返回return dp[n];}
};

?Leetcode 測試結果：??

?5、不同路徑（medium）

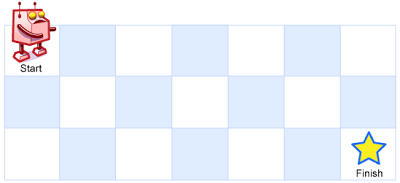
一個機器人位于一個?m x n?網格的左上角 （起始點在下圖中標記為 “Start” ）。

機器人每次只能向下或者向右移動一步。機器人試圖達到網格的右下角（在下圖中標記為 “Finish” ）。

問總共有多少條不同的路徑？

?

示例 1：

輸入：m = 3, n = 7
輸出：28

示例 2：

輸入：m = 3, n = 2
輸出：3
解釋：
從左上角開始，總共有 3 條路徑可以到達右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

輸入：m = 7, n = 3
輸出：28

示例 4：

輸入：m = 3, n = 3
輸出：6

提示：

  • 1 <= m, n <= 100
  • 題目數據保證答案小于等于?2 * 109

a、解題思路?

看我們題目后，根據經驗此題位動態規劃解題

1、轉態表示

首先我們想以i，j位置為結尾表示什么

dp[i][j表示：以i,j位置結尾的時候，機器人到這里有多少條路徑

?2、狀態轉移方程

根據最近的一個位置劃分

我要求到[i,j]?路徑，本質上就是求dp[i - 1][j] + dp[i][j - 1]的路徑和

所以狀態轉移方法為

dp[i][j] = dp[i-1][j]+dp[i][j-1];

3、初始化

這里我們要初始化，就是在二維數組多開一行和一列，但我們要思路多開的行列填什么呢（一切都是為了填表走服務）？，很明顯，在根據dp[i][j] = dp[i-1][j]+dp[i][j-1];填寫表格的時候，走一步就到終點，那最外層從從到都應該填1（dp[i][j表示：以i,j位置結尾的時候，機器人到這里有多少條路徑），為達到這不目的，應該把dp[0][1]=1其余為0。

4、?填表順序

從上往下填寫每一行，每一行都是從左往又開始填寫?

5、返回值

dp[m][n]

b、代碼

class Solution {
public:int uniquePaths(int m, int n){//創建二維dp表vector<vector<int>> dp(m + 1, vector<int>(n + 1));//初始化dp[0][1] = 1;//填表for (int i = 1; i <= m; i++){for (int j = 1; j <= n; j++){dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m][n];}
};

?Leetcode 測試結果：???

?

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/719352.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/719352.shtml
英文地址，請注明出處：http://en.pswp.cn/news/719352.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

Java基礎 - 模擬醫院掛號系統

Java基礎 - 模擬醫院掛號系統

模擬醫院掛號系統功能 1. 科室管理：新增科室，刪除科室（如果有醫生在，則不能刪除該科室），修改科室 2. 醫生管理：錄入醫生信息以及科室信息，修改醫生信息（主要是修改個人信息和科室） 3. 坐診信息設置：可以設置醫生當天和未來6天的坐診情況，包括上午和下午的坐診時…
閱讀更多...
Linux設備模型(九) - bus/device/device_driver/class

Linux設備模型(九) - bus/device/device_driver/class

一&#xff0c;設備驅動模型 1&#xff0c;概述 在前面寫的驅動中&#xff0c;我們發現編寫驅動有個固定的模式只有往里面套代碼就可以了&#xff0c;它們之間的大致流程可以總結如下&#xff1a; 實現入口函數xxx_init()和卸載函數xxx_exit() 申請設備號 register_chrdev_r…
閱讀更多...
Spring源碼：手寫SpringDI

Spring源碼：手寫SpringDI

我們是在實現了SpringIOC的基礎上&#xff0c;進行拓展&#xff0c;IOC實現源碼可以查看&#xff1a;手寫SpringIOC 文章目錄 一、分析二、實現1、構造注入1&#xff09;分析2&#xff09;版本1BeanReferenceBeanDefinitionGenericBeanDefinitionDefaultBeanFactory1、改造構造…
閱讀更多...
install Ubuntu again

install Ubuntu again

參考鏈接&#xff1a;Windows 下安裝 Ubuntu 雙系統(更新) - duan22677 - 博客園 這里的總的空間是120G 它里面指出雙系統的時候&#xff0c;/boot 應該是主分區 參考鏈接&#xff1a;win10下安裝Ubuntu16.04雙系統_windows10安裝引導ubuntu-CSDN博客 這里面講到了&#xf…
閱讀更多...
ES入門六：Suggesters Api實踐

ES入門六：Suggesters Api實踐

都是負擔在很多app上&#xff0c;當我們輸入某些內容時候&#xff0c;它會立即做一些補全操作&#xff0c;如果我想實現上述的需求&#xff0c;我們就可以使用ES提供的Suggesters Api。那Suggesters是如何做到的那&#xff1f;簡單來說&#xff0c;Suggesters會將輸入的文本拆分…
閱讀更多...
【網站項目】167固定資產管理系統

【網站項目】167固定資產管理系統

&#x1f64a;作者簡介&#xff1a;擁有多年開發工作經驗&#xff0c;分享技術代碼幫助學生學習&#xff0c;獨立完成自己的項目或者畢業設計。 代碼可以私聊博主獲取。&#x1f339;贈送計算機畢業設計600個選題excel文件&#xff0c;幫助大學選題。贈送開題報告模板&#xff…
閱讀更多...
誰才是“內卷”之王？眾多洗地機品牌哪家清潔力最強？清潔最干凈？

誰才是“內卷”之王？眾多洗地機品牌哪家清潔力最強？清潔最干凈？

在如今快節奏的生活中&#xff0c;家庭清潔工作愈發顯得繁瑣而耗時。添可洗地機憑借其高效的一體化清潔功能和智能化操作&#xff0c;為現代家庭生活帶來了極大的便利。面對眾多款品牌洗地機型號&#xff0c;消費者不禁會問&#xff1a;哪家洗地機清潔力最強&#xff1f;在性能…
閱讀更多...
解決tomcat雙擊startup.bat一閃而過的問題

解決tomcat雙擊startup.bat一閃而過的問題

這種問題可能是tomcat找不到你的jdk環境配置路徑 1、首先在tomcat的bin文件夾找到startup.bat 和catalina.bat兩個文件 2、startup.bat用記事本打開 在末尾添加pause 3、保存修改&#xff0c;雙擊startup.bat如果出現這種問題&#xff0c;就是找不到jdk路徑 4、用記事本打開ca…
閱讀更多...
2194. 負載平衡問題（網絡流，費用流）

2194. 負載平衡問題（網絡流，費用流）

活動 - AcWing G 公司有 n 個沿鐵路運輸線環形排列的倉庫&#xff0c;每個倉庫存儲的貨物數量不等。 如何用最少搬運量可以使 n 個倉庫的庫存數量相同。 搬運貨物時&#xff0c;只能在相鄰的倉庫之間搬運。 數據保證一定有解。 輸入格式 第 1 行中有 1 個正整數 n&#x…
閱讀更多...
MySQL - 聯表查詢從表即使有索引依然 ALL 的一個原因

MySQL - 聯表查詢從表即使有索引依然 ALL 的一個原因

問題描述 今天排查 MySQL 語句性能發現&#xff0c;主外鍵都添加索引了&#xff0c;為什么 explain 分析 type ALL&#xff1f; 原因分析 主表和從表的關聯字段的編碼方式不一樣&#xff0c;改成一樣的編碼方式即可 解決方案 # 修改某張表某字段編碼 ALTER TABLE t_xxx CHA…
閱讀更多...
STM32CubeMX實戰教程: TIM6、TIM7 - 基本定時器

STM32CubeMX實戰教程: TIM6、TIM7 - 基本定時器

目錄 一、基本定時器的作用 二、常用型號的TIM時鐘頻率 三、CubeMX配置 四、編寫執行代碼 一、基本定時器的作用 基本定時器&#xff0c;主要用于實現定時和計數功能。作用包括&#xff1a; 定時功能&#xff1a;可以產生周期性的中斷&#xff0c;用于實現定時任務。例如&…
閱讀更多...
什么是Docker容器？

什么是Docker容器？

Docker是一種輕量級的虛擬化技術&#xff0c;同時是一個開源的應用容器運行環境搭建平臺&#xff0c;可以讓開發者以便捷方式打包應用到一個可移植的容器中&#xff0c;然后安裝至任何運行Linux或Windows等系統的服務器上。相較于傳統虛擬機&#xff0c;Docker容器提供輕量化的…
閱讀更多...
【C++通關攻略 · 基礎篇】輸入輸出語句

【C++通關攻略 · 基礎篇】輸入輸出語句

目錄 輸入語句 原理 什么是流&#xff1f; 語法 補充 輸出語句 原理 語法 補充 示例 輸入語句 輸入語句&#xff0c;就是用來接受用戶輸入的內容。比如用戶在控制臺輸入一個數字&#xff0c;就可以用輸入語句去就收。 原理 在 C 中&#xff0c;cin 就是最常用的輸入…
閱讀更多...
linux安裝mysql5.7

linux安裝mysql5.7

linux安裝mysql5.7 一、下載mysql5.7二、解壓包介紹三、上傳包到linux四、卸載mariadb五、安裝mysql六、修改權限七、啟動mysql八、使用過navicat創作不易&#xff0c;筆記不易&#xff0c;如覺不錯&#xff0c;請三連&#xff0c;謝謝~~ 一、下載mysql5.7 去mysql官方下載&am…
閱讀更多...
MES系統在離散制造企業中的功能解析

MES系統在離散制造企業中的功能解析

隨著信息技術的快速發展和制造業的轉型升級&#xff0c;MES在離散制造企業中的作用日益凸顯。MES系統不僅提高了生產效率和產品質量&#xff0c;還優化了資源配置&#xff0c;增強了企業的市場競爭力。 一、生產管理功能 MES系統能夠實時監控生產現場的各種數據&#xff0c;包…
閱讀更多...
二叉搜索樹題目：將有序數組轉換為二叉搜索樹

二叉搜索樹題目：將有序數組轉換為二叉搜索樹

文章目錄 題目標題和出處難度題目描述要求示例數據范圍 解法思路和算法證明代碼復雜度分析 題目 標題和出處 標題&#xff1a;將有序數組轉換為二叉搜索樹 出處&#xff1a;108. 將有序數組轉換為二叉搜索樹 難度 4 級 題目描述 要求 給定整數數組 nums \texttt{nums}…
閱讀更多...
一、低代碼平臺-數據庫設計規范

一、低代碼平臺-數據庫設計規范

數據庫設計規范目的 a、規格化管理各個業務數據表 b、通過字段名稱快速了解表與表之間的關聯關系 c、通過字段第一位快速了解字段數據類型等等所有規范都為了更好的開發與后期系統運維。 1、數據庫設計規范 答&#xff1a;數據庫安裝必須選擇大小寫敏感&#xff1b;編碼格式…
閱讀更多...
15 easy 141. 環形鏈表

15 easy 141. 環形鏈表

法1&#xff1a;快慢指針法&#xff1a; //給你一個鏈表的頭節點 head &#xff0c;判斷鏈表中是否有環。 // // 如果鏈表中有某個節點&#xff0c;可以通過連續跟蹤 next 指針再次到達&#xff0c;則鏈表中存在環。 為了表示給定鏈表中的環&#xff0c;評測系統內部使用整數…
閱讀更多...
Python爬蟲副業真的可行嗎？

Python爬蟲副業真的可行嗎？

首先回答你&#xff0c;是可行的&#xff0c;python爬蟲能當副業&#xff0c;副業的方式比較多&#xff0c;等下我會講幾種。 那學到哪個層次可以接單呢&#xff1f;主要看你是接什么樣的單&#xff0c;爬一些資料&#xff0c;視頻這種簡單的學一兩個月就沒什么問題&#xff0…
閱讀更多...
第一天 走進Docker的世界

第一天 走進Docker的世界

第一天 走進Docker的世界 介紹docker的前世今生&#xff0c;了解docker的實現原理&#xff0c;以Django項目為例&#xff0c;帶大家如何編寫最佳的Dockerfile構建鏡像。通過本章的學習&#xff0c;大家會知道docker的概念及基本操作&#xff0c;并學會構建自己的業務鏡像&…
閱讀更多...
最新文章

Copyright @ 2022~2023