文章目錄
- 題目
- 標題和出處
- 難度
- 題目描述
- 要求
- 示例
- 數據范圍
- 解法
- 思路和算法
- 證明
- 代碼
- 復雜度分析
題目
標題和出處
標題:將有序數組轉換為二叉搜索樹
出處:108. 將有序數組轉換為二叉搜索樹
難度
4 級
題目描述
要求
給定整數數組 nums \texttt{nums} nums,其中元素已經按升序排列,將其轉換為高度平衡二叉搜索樹。
高度平衡二叉樹滿足每個結點的左右子樹的高度差的絕對值不超過 1 \texttt{1} 1。
示例
示例 1:
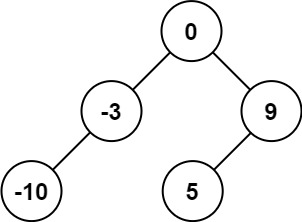
輸入: nums = [-10,-3,0,5,9] \texttt{nums = [-10,-3,0,5,9]} nums?=?[-10,-3,0,5,9]
輸出: [0,-3,9,-10,null,5] \texttt{[0,-3,9,-10,null,5]} [0,-3,9,-10,null,5]
解釋: [0,-10,5,null,-3,null,9] \texttt{[0,-10,5,null,-3,null,9]} [0,-10,5,null,-3,null,9] 也將被視為正確答案:
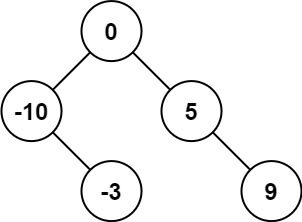
示例 2:
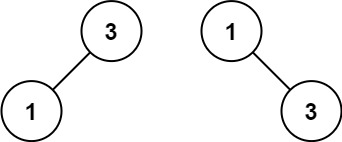
輸入: nums = [1,3] \texttt{nums = [1,3]} nums?=?[1,3]
輸出: [3,1] \texttt{[3,1]} [3,1]
解釋: [1,null,3] \texttt{[1,null,3]} [1,null,3] 和 [3,1] \texttt{[3,1]} [3,1] 都是高度平衡二叉搜索樹。
數據范圍
- 1 ≤ nums.length ≤ 10 4 \texttt{1} \le \texttt{nums.length} \le \texttt{10}^\texttt{4} 1≤nums.length≤104
- -10 4 ≤ nums[i] ≤ 10 4 \texttt{-10}^\texttt{4} \le \texttt{nums[i]} \le \texttt{10}^\texttt{4} -104≤nums[i]≤104
- nums \texttt{nums} nums 按嚴格遞增順序排列
解法
思路和算法
由于二叉搜索樹的中序遍歷序列是單調遞增的,因此給定的升序數組即為二叉搜索樹的中序遍歷序列。在只有中序遍歷序列的情況下,無法唯一地確定二叉搜索樹。
為了得到高度平衡二叉搜索樹,構造的二叉搜索樹應滿足根結點的左子樹和右子樹的結點數盡可能接近。當結點總數是奇數時,根結點值應為中序遍歷序列的中間位置的結點值,根結點的左子樹和右子樹的結點數應相等;當結點總數是偶數時,根結點值應為中序遍歷序列的中間位置的兩個結點值之一,根結點的左子樹和右子樹的結點數之差的絕對值應等于 1 1 1。
確定高度平衡二叉搜索樹的根結點之后,其余的結點值分別位于根結點的左子樹和右子樹中,數組中位于根結點左側的值都在左子樹中,數組中位于根結點右側的值都在右子樹中,左子樹和右子樹也是高度平衡二叉搜索樹。可以通過數學歸納法證明,如果兩個高度平衡二叉搜索樹的結點數之差的絕對值不超過 1 1 1,則這兩個高度平衡二叉搜索樹的高度之差的絕對值不超過 1 1 1。
由于高度平衡二叉搜索樹的每個子樹也都是高度平衡二叉搜索樹,每個子樹包含的結點值的集合對應給定的數組中的連續子數組,因此可以使用遞歸的方式構造高度平衡二叉搜索樹,遞歸的過程中只要指定每個子樹包含的結點值的集合對應的連續子數組的下標區間 [ start , end ] [\textit{start}, \textit{end}] [start,end] 即可。
遞歸的終止條件是下標區間為空,即 start > end \textit{start} > \textit{end} start>end,此時對應的子樹為空。對于其余情況,首先根據 start \textit{start} start 和 end \textit{end} end 計算得到根結點值的下標 mid \textit{mid} mid 并使用該結點值創建根結點,然后分別使用下標區間 [ start , mid ? 1 ] [\textit{start}, \textit{mid} - 1] [start,mid?1] 和 [ mid + 1 , end ] [\textit{mid} + 1, \textit{end}] [mid+1,end] 創建根結點的左子樹和右子樹。
當 start ≤ end \textit{start} \le \textit{end} start≤end 時, mid \textit{mid} mid 的取值的唯一性取決于下標區間 [ start , end ] [\textit{start}, \textit{end}] [start,end] 內的元素個數的奇偶性。如果下標區間 [ start , end ] [\textit{start}, \textit{end}] [start,end] 內的元素個數是奇數,則 mid \textit{mid} mid 的取值是唯一的;如果下標區間 [ start , end ] [\textit{start}, \textit{end}] [start,end] 內的元素個數是偶數,則 mid \textit{mid} mid 的取值是不唯一的,可以是中間位置左邊的下標或者中間位置右邊的下標。
-
當 mid = ? start + end 2 ? \textit{mid} = \Big\lfloor \dfrac{\textit{start} + \textit{end}}{2} \Big\rfloor mid=?2start+end?? 時, mid \textit{mid} mid 是中間位置左邊的下標。
-
當 mid = ? start + end + 1 2 ? \textit{mid} = \Big\lfloor \dfrac{\textit{start} + \textit{end} + 1}{2} \Big\rfloor mid=?2start+end+1?? 時, mid \textit{mid} mid 是中間位置右邊的下標。
如果下標區間 [ start , end ] [\textit{start}, \textit{end}] [start,end] 內的元素個數是奇數,則上述兩種方法計算得到的 mid \textit{mid} mid 的值相同。
由此可以得到三種構造高度平衡二叉搜索樹的方法。
-
每次都將根結點值取為中間位置左邊的下標處的值。
-
每次都將根結點值取為中間位置右邊的下標處的值。
-
每次隨機將根結點值取為中間位置左邊或右邊的下標處的值。
證明
為了證明上述構造高度平衡二叉搜索樹的方法的正確性,需要證明:如果兩個高度平衡二叉搜索樹的結點數之差的絕對值不超過 1 1 1,則這兩個高度平衡二叉搜索樹的高度之差的絕對值不超過 1 1 1。
用 h ( n ) h(n) h(n) 表示有 n n n 個結點的高度平衡二叉搜索樹的高度,其中 n ≥ 1 n \ge 1 n≥1,規定 h ( 1 ) = 0 h(1) = 0 h(1)=0, h ( 2 ) = h ( 3 ) = 1 h(2) = h(3) = 1 h(2)=h(3)=1,則對于 1 ≤ n ≤ 3 1 \le n \le 3 1≤n≤3 有 h ( n ) = ? log ? n ? h(n) = \lfloor \log n \rfloor h(n)=?logn?。
當 n ≥ 4 n \ge 4 n≥4 時,假設對于任意 1 ≤ m < n 1 \le m < n 1≤m<n 都有 h ( m ) = ? log ? m ? h(m) = \lfloor \log m \rfloor h(m)=?logm?,需要證明 h ( n ) = ? log ? n ? h(n) = \lfloor \log n \rfloor h(n)=?logn?。
-
當 n n n 是奇數時,令 n = 2 k + 1 n = 2k + 1 n=2k+1,其中 k ≥ 1 k \ge 1 k≥1,則根結點的左子樹和右子樹各有 k k k 個結點。由于 k < n k < n k<n,因此 h ( k ) = ? log ? k ? h(k) = \lfloor \log k \rfloor h(k)=?logk? 已知,此時 h ( n ) = h ( k ) + 1 = ? log ? k ? + 1 h(n) = h(k) + 1 = \lfloor \log k \rfloor + 1 h(n)=h(k)+1=?logk?+1。由于 n = 2 k + 1 n = 2k + 1 n=2k+1,因此 n ? 1 = 2 k n - 1 = 2k n?1=2k, log ? ( n ? 1 ) = log ? 2 k = log ? k + 1 \log (n - 1) = \log 2k = \log k + 1 log(n?1)=log2k=logk+1,取整得 ? log ? ( n ? 1 ) ? = ? log ? k ? + 1 \lfloor \log (n - 1) \rfloor = \lfloor \log k \rfloor + 1 ?log(n?1)?=?logk?+1。由于 n n n 是奇數,因此 ? log ? n ? = ? log ? ( n ? 1 ) ? \lfloor \log n \rfloor = \lfloor \log (n - 1) \rfloor ?logn?=?log(n?1)?, ? log ? n ? = ? log ? k ? + 1 \lfloor \log n \rfloor = \lfloor \log k \rfloor + 1 ?logn?=?logk?+1, h ( n ) = ? log ? n ? h(n) = \lfloor \log n \rfloor h(n)=?logn?。
-
當 n n n 是偶數時,令 n = 2 k + 2 n = 2k + 2 n=2k+2,其中 k ≥ 1 k \ge 1 k≥1,則根結點的左子樹和右子樹分別有 k k k 個結點和 k + 1 k + 1 k+1 個結點。由于 k + 1 < n k + 1 < n k+1<n,因此 h ( k + 1 ) = ? log ? ( k + 1 ) ? h(k + 1) = \lfloor \log (k + 1) \rfloor h(k+1)=?log(k+1)? 已知,此時 h ( n ) = h ( k + 1 ) + 1 = ? log ? ( k + 1 ) ? + 1 h(n) = h(k + 1) + 1 = \lfloor \log (k + 1) \rfloor + 1 h(n)=h(k+1)+1=?log(k+1)?+1。由于 n = 2 k + 2 = 2 ( k + 1 ) n = 2k + 2 = 2(k + 1) n=2k+2=2(k+1),因此 log ? n = log ? 2 ( k + 1 ) = log ? ( k + 1 ) + 1 \log n = \log 2(k + 1) = \log (k + 1) + 1 logn=log2(k+1)=log(k+1)+1,取整得 ? log ? n ? = ? log ? ( k + 1 ) ? + 1 \lfloor \log n \rfloor = \lfloor \log (k + 1) \rfloor + 1 ?logn?=?log(k+1)?+1, h ( n ) = ? log ? n ? h(n) = \lfloor \log n \rfloor h(n)=?logn?。
因此對于任意正整數 n n n,都有 h ( n ) = ? log ? n ? h(n) = \lfloor \log n \rfloor h(n)=?logn?。由于任意兩個相鄰正整數的對數之差一定不超過 1 1 1,因此當 n ≥ 2 n \ge 2 n≥2 時,一定有 h ( n ) ? h ( n ? 1 ) ≤ 1 h(n) - h(n - 1) \le 1 h(n)?h(n?1)≤1。
代碼
下面的代碼為每次都將根結點值取為中間位置左邊的下標處的值的做法。
class Solution {public TreeNode sortedArrayToBST(int[] nums) {return createBST(nums, 0, nums.length - 1);}public TreeNode createBST(int[] nums, int start, int end) {if (start > end) {return null;}int mid = (end - start) / 2 + start;return new TreeNode(nums[mid], createBST(nums, start, mid - 1), createBST(nums, mid + 1, end));}
}
下面的代碼為每次都將根結點值取為中間位置右邊的下標處的值的做法。
class Solution {public TreeNode sortedArrayToBST(int[] nums) {return createBST(nums, 0, nums.length - 1);}public TreeNode createBST(int[] nums, int start, int end) {if (start > end) {return null;}int mid = (end - start + 1) / 2 + start;return new TreeNode(nums[mid], createBST(nums, start, mid - 1), createBST(nums, mid + 1, end));}
}
下面的代碼為每次隨機將根結點值取為中間位置左邊或右邊的下標處的值的做法。
class Solution {public TreeNode sortedArrayToBST(int[] nums) {return createBST(nums, 0, nums.length - 1);}public TreeNode createBST(int[] nums, int start, int end) {if (start > end) {return null;}int mid = (end - start + (int) (Math.random() * 2)) / 2 + start;return new TreeNode(nums[mid], createBST(nums, start, mid - 1), createBST(nums, mid + 1, end));}
}
復雜度分析
-
時間復雜度: O ( n ) O(n) O(n),其中 n n n 是數組 nums \textit{nums} nums 的長度。每個元素都被訪問一次。
-
空間復雜度: O ( log ? n ) O(\log n) O(logn),其中 n n n 是數組 nums \textit{nums} nums 的長度。空間復雜度主要是遞歸調用的棧空間,由于構造的是高度平衡二叉搜索樹,因此遞歸調用棧的深度是 O ( log ? n ) O(\log n) O(logn)。注意返回值不計入空間復雜度。








![[環境配置]ssh連接報錯“kex_exchange_identification: read: Connection reset by peer”](http://pic.xiahunao.cn/[環境配置]ssh連接報錯“kex_exchange_identification: read: Connection reset by peer”)
)








![Linux基礎命令[10]-cmp](http://pic.xiahunao.cn/Linux基礎命令[10]-cmp)
