代碼過程

訓練過程：

1. 準備數據集
2. 設計模型（用來計算 $\hat{y}$）
3. 構造損失函數和優化器（API）
4. 訓練周期（前饋、反饋、更新）

準備數據

這里的輸入輸出數據均表示為3×1的，也就是維度均為1

# 行表示實例數量，列表示維度feature
import torch
x_data=torch.Tensor([[1.0],[2.0],[3.0]])
y_data=torch.Tensor([[2.0],[4.0],[6.0]])

設計模型

模型繼承Module類，并且必須要實現 init 和 forward 兩個方法，其中self.linear=torch.nn.Linear(1,1)表示實例化Linear類，這個類是可調用的，其__call__函數調用了 forward 方法

class LinearModel(torch.nn.Module):def __init__(self):super(LinearModel,self).__init__()# weight 和 bias 1 1 self.linear=torch.nn.Linear(1,1)def forward(self,x):# callabley_pred=self.linear(x)return y_pred# callable
model=LinearModel()

pytorch中的linear類是在某一個數據上應用線性轉換，其公式表達為 $y=x{w}^T+b$

class torch.nn.Linear(in_features,out_features,bias=True) ：其中in_features和out_features分別表示輸入和輸出的數據的維度（列的數量），bias表示偏置，默認是true，該類有兩個參數

• weight：可學習參數，值從均勻分布$U(?\sqrt{k},\sqrt{k})$中獲取，其中 $k=\frac{1}{in\_features}$
• bias：shape和輸出的維度一樣，也是從分布$U(?\sqrt{k},\sqrt{k})$中初始化的
  

設計構造函數與優化器

# 構造損失函數和優化器
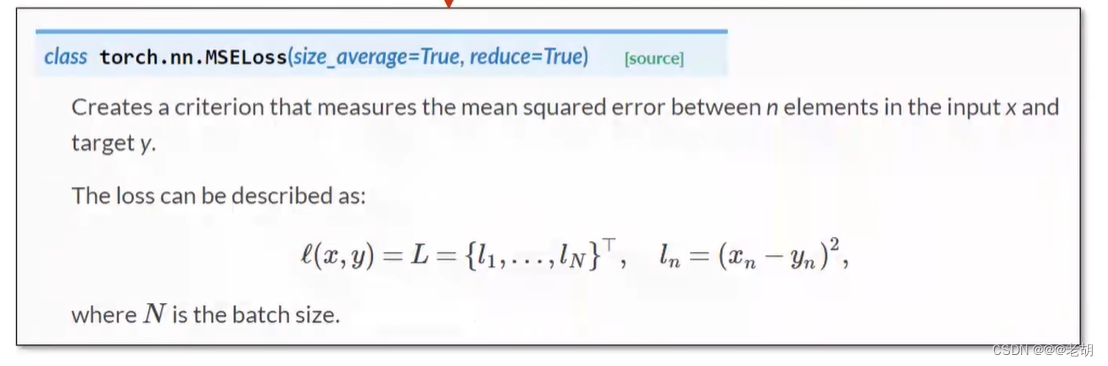
criterion=torch.nn.MSELoss(size_average=False)# w和b--->parameters
opyimizer=torch.optim.SGD(model.parameters(),lr=0.01)

訓練過程

# 訓練過程
for epoch in range(100):y_pred=model(x_data)loss=criterion(y_pred,y_data)# loss標量，自動調用__str__()print(epoch,loss)optimizer.zero_grad()# backwardloss.backward()# updateoptimizer.step()

訓練代碼和結果

# 行表示實例數量，列表示維度feature
import torch
x_data=torch.Tensor([[1.0],[2.0],[3.0]])
y_data=torch.Tensor([[2.0],[4.0],[6.0]])class LinearModel(torch.nn.Module):def __init__(self):super(LinearModel,self).__init__()# weight 和 bias 1 1 self.linear=torch.nn.Linear(1,1)def forward(self,x):# callabley_pred=self.linear(x)return y_pred# callable
model=LinearModel()# 構造損失函數和優化器
criterion=torch.nn.MSELoss(size_average=False)
optimizer=torch.optim.SGD(model.parameters(),lr=0.01)# 訓練過程
for epoch in range(100):y_pred=model(x_data)loss=criterion(y_pred,y_data)# loss標量，自動調用__str__()print(epoch,loss)optimizer.zero_grad()# backwardloss.backward()# updateoptimizer.step()# 打印信息
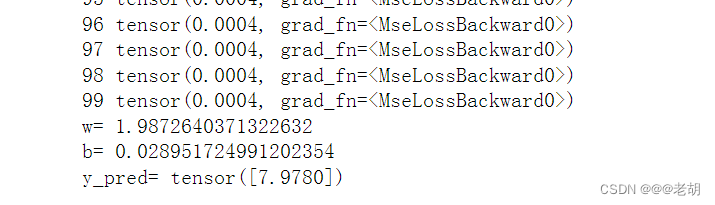
print('w=',model.linear.weight.item())
print('b=',model.linear.bias.item())x_test=torch.Tensor([4.0])
y_test=model(x_test)
print('y_pred=',y_test.data)

---

pytorch中的Linear層的底層原理（個人喜歡，不用看）

我們在課本使用到的線性函數的基本公式表達為$y=x{w}^T+b$，但是在Linear層中，當輸入特征被Linear層接收是，它會接收后轉置，然后乘以權重矩陣，得到的是輸出特征的轉置，換句話說可以在底層使用Linear，它實際上做的是$y^T=w{x}^T+b$。可以使用下面的案例進行驗證：

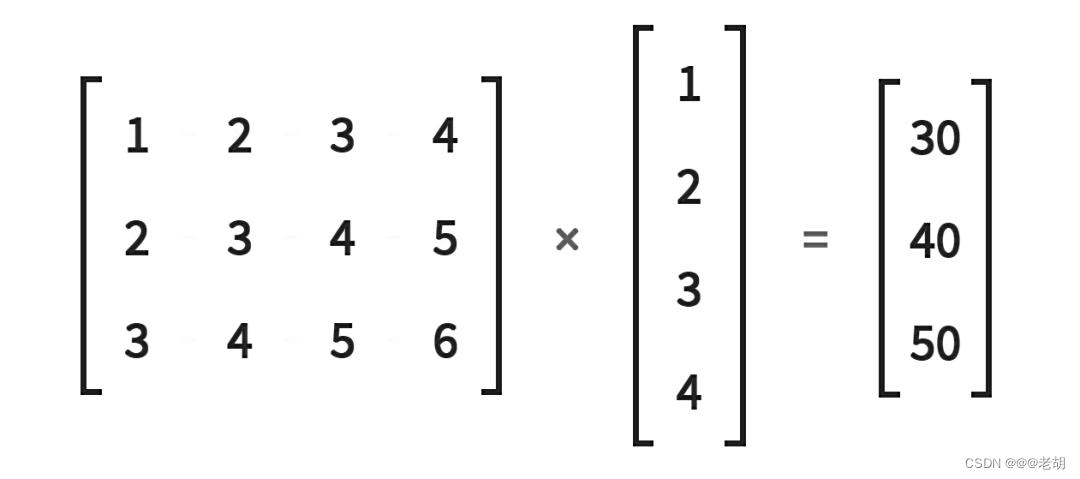
普通矩陣乘法實現

很明顯，上面的圖標表示一個 3×4 的矩陣乘以 4×1 的矩陣，得到一個 3×1 的輸出矩陣，使用普通矩陣的乘法實現如下。

import torchin_features=torch.tensor([1,2,3,4],dtype=torch.float32)
weight_matrix=torch.tensor([[1,2,3,4],[2,3,4,5],[3,4,5,6]
],dtype=torch.float32)weight_matrix.matmul(in_features)# 矩陣乘法

實現截圖：

Linear層實現

# 這里還是使用上面使用過的數據
import torch
in_features=torch.tensor([1,2,3,4],dtype=torch.float32)
weight_matrix=torch.tensor([[1,2,3,4],[2,3,4,5],[3,4,5,6]
],dtype=torch.float32)print(weight_matrix.matmul(in_features))# 矩陣乘法fc = torch.nn.Linear(in_features=4, out_features=3, bias=False)
# 這里是隨機一個權重矩陣
print('fc.weight',fc.weight)
fc(in_features)

輸出結果：

print('fc.weight',fc.weight)# 使用上面的權重矩陣進行計算
fc.weight = torch.nn.Parameter(weight_matrix)
print('fc.weight',fc.weight)
fc(in_features)

結果截圖：

可以看到上面截圖與下面的截圖的區別，一開始隨機一個權重的時候，進行運算，使用到前面提及到的權重矩陣后，Linear層進行運算之后，得到與使用普通矩陣乘法一樣的結果，相同的結果說明，Linear底層的實現與上面的矩陣乘法的邏輯是一致的。

以上的論證可以說明，Linear的底層實現其實是$y^T=w{x}^T+b$，而不是$y=x{w}^T+b$，可能會有人好奇，為什么書本上都是寫的后者而不是寫前者，其實本質上二者都一樣，前者的轉置就是后者。

回調機制

在pytorch學習（一）線性模型中，第一個代碼中，我們沒有通過pytorch實現線性模型的時候，我們會顯式調用forward函數，計算前饋的值，我們是這樣寫的y_pred_val=forward(x_val)，但是在使用pytorch之后，我們是這樣寫的y_pred=model(x_data)，直接實例化一個對象，然后通過對象直接計算預測值（前饋值），但是并沒有使用到forward函數。這是因為pytorch模塊類中實現了python中一個特殊的函數，也就是回調函數。

如果一個類實現了回調方法，那么只要對象實例被調用，這個特殊的方法也會被調用。我們不直接調用forward()方法，而是調用對象實例。在對象實例被調用之后，在底層調用了__ call __方法，然后調用了forward()方法。這適用于所有的PyTorch神經網絡模塊。

以上僅代表小白個人學習觀點，如有錯誤歡迎批評指正。

參考