The Closest Fibonacci Number
The?Fibonacci sequence?Fn??is defined by?Fn+2?=Fn+1?+Fn??for?n≥0, with?F0?=0?and?F1?=1. The?closest Fibonacci number?is defined as the Fibonacci number with the smallest absolute difference with the given integer?N.
Your job is to find the closest Fibonacci number for any given?N.
Input Specification:
Each input file contains one test case, which gives a positive integer?N?(≤10^8).
Output Specification:
For each case, print the closest Fibonacci number. If the solution is not unique, output the smallest one.
Sample Input:
305
Sample Output:
233
Hint:
Since part of the sequence is { 0, 1, 1, 2, 3, 5, 8, 12, 21, 34, 55, 89, 144, 233, 377, 610, ... }, there are two solutions: 233 and 377, both have the smallest distance 72 to 305. The smaller one must be printed out.
題意:輸入一個n,輸出離他最相近的斐波那契數。
解析:因為n的范圍在1e8之內,我們直接暴力遍歷一定范圍內的斐波那契數與答案取min即可。
#include <bits/stdc++.h>
using namespace std;
const int N=1e3+5;
int a[N];
void solve()
{int n,mi,ans=1;scanf("%d",&n);a[1]=a[2]=1;mi=n-1;//初始最小距離直接取跟1for(int i=3;;i++){a[i]=a[i-1]+a[i-2];if(abs(n-a[i])<mi) mi=abs(n-a[i]),ans=a[i];//更新即可if(a[i]>1e9) break;//如果大于1e9,那么最近數肯定已經取到了}printf("%d\n",ans);
}
int main()
{int t=1;//scanf("%d",&t);while(t--) solve();return 0;
}Subsequence in Substring
A?substring?is a continuous part of a string. A?subsequence?is the part of a string that might be continuous or not but the order of the elements is maintained. For example, given the string?atpaaabpabtt,?pabt?is a substring, while?pat?is a subsequence.
Now given a string?S?and a subsequence?P, you are supposed to find the shortest substring of?S?that contains?P. If such a solution is not unique, output the left most one.
Input Specification:
Each input file contains one test case which consists of two lines. The first line contains?S?and the second line?P.?S?is non-empty and consists of no more than?104?lower English letters.?P?is guaranteed to be a non-empty subsequence of?S.
Output Specification:
For each case, print the shortest substring of?S?that contains?P. If such a solution is not unique, output the left most one.
Sample Input:
atpaaabpabttpcat
pat
Sample Output:
pabt題意:給兩個字符串a b,要求你在a中找出一段子串的子序列是b,輸出滿足條件的最短且最左的子串。
解法一:不懂,居然直接暴力匹配就行了,而且還跑的比"優化的"還快。。
#include <bits/stdc++.h>
using namespace std;
const int N=1e4+5;
void solve()
{string a,b,ans;cin>>a>>b;int ans_len=1e9;//答案字符串長度for(int i=0;i<a.size();i++){if(a[i]!=b[0]) continue;string x;for(int j=i,k=0;j<a.size();j++){if(a[j]==b[k]) k++;x+=a[j];if(k==b.size())//匹配完成{if(j-i+1<ans_len) ans_len=j-i+1,ans=x;//更新break;}}}cout<<ans<<"\n";
}
int main()
{int t=1;//scanf("%d",&t);while(t--) solve();return 0;
}解法二:建一個pos[N][30]來記錄第i位開始往后某個字母最近的位置,pos數組可以從后往前遍歷建造,復雜度是O(N*26),然后匹配時候就可以跳著進行,復雜度卡線,抖動過題😥
#include <bits/stdc++.h>
using namespace std;
const int N=1e4+5;
char a[N],b[N];
int pos[N][30];
void solve()
{scanf("%s%s",a+1,b+1);int n=strlen(a+1),m=strlen(b+1);for(int i=n;i>=1;i--)//記錄第i位開始往后某個字母最近的位置{for(int j=1;j<=26;j++) pos[i][j]=pos[i+1][j];pos[i][a[i]-'a'+1]=i;}int ans_len=1e9,ansl=-1,ansr=-1;for(int i=1;i<=n;i++){if(a[i]==b[1]){int l=i,r=i,k=2;while(pos[r+1][b[k]-'a'+1]!=0&&k<=m)//注意要從r+1開始,避免相同字母導致原地跳{r=pos[r+1][b[k]-'a'+1];if(r-l+1>=ans_len) break;//剪枝..k++;}if(k==m+1&&r-l+1<ans_len) ans_len=r-l+1,ansl=l,ansr=r;}}for(int i=ansl;i<=ansr;i++) printf("%c",a[i]);printf("\n");
}
int main()
{int t=1;//scanf("%d",&t);while(t--) solve();return 0;
}File Path?
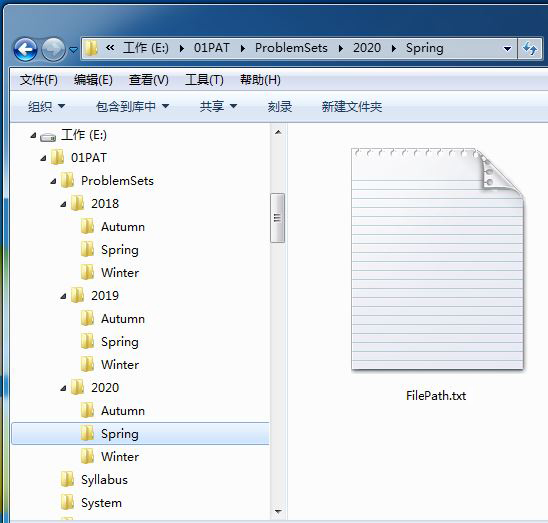
The figure shows the tree view of directories in Windows File Explorer. When a file is selected, there is a file path shown in the above navigation bar. Now given a tree view of directories, your job is to print the file path for any selected file.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer?N?(≤103), which is the total number of directories and files. Then?N?lines follow, each gives the unique 4-digit ID of a file or a directory, starting from the unique root ID?0000. The format is that the files of depth?d?will have their IDs indented by?d?spaces. It is guaranteed that there is no conflict in this tree structure.
Then a positive integer?K?(≤100) is given, followed by?K?queries of IDs.
Output Specification:
For each queried?ID, print in a line the corresponding path from the root to the file in the format:?0000->ID1->ID2->...->ID. If the?ID?is not in the tree, print?Error: ID is not found.?instead.
Sample Input:
14
00001234223432344234423523335234623472349999000182340002
4 9999 8234 0002 6666
Sample Output:
0000->1234->2234->6234->7234->9999
0000->1234->0001->8234
0000->0002
Error: 6666 is not found.題意:如圖所示,給n個文件,空格的個數就是深度,有q個詢問,要求輸出該文件的路徑或者報告不存在。
解析: 空格的個數其實就是文件的深度,而一個文件的父親一定在它的上方,數據較小,直接往上不斷尋找深度比自身小1的就是父親文件。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e3+5;
string str[N];
map<string,int> dep;//記錄每個文件夾的"深度"
map<string,string> fa;//記錄該文件夾歸屬哪個文件
void solve()
{int n;scanf("%d",&n);getchar();//下方要getline,需要吃掉scanf的回車for(int i=1;i<=n;i++){string name;getline(cin,str[i]);int cnt=0;for(int j=0;j<str[i].size();j++){if(str[i][j]==' ') cnt++;//空格個數就是深度else name+=str[i][j];}dep[name]=cnt;str[i]=name;if(name=="0000") continue;for(int j=i-1;j>=1;j--)//直接從此往上暴力尋找父親{if(dep[str[j]]==cnt-1){fa[name]=str[j];break;}}}int q;scanf("%d",&q);fa["0000"]="0000";//根目錄父親是本身while(q--){string x;cin>>x;if(fa[x]=="")//找不到{printf("Error: ");cout<<x;printf(" is not found.\n");continue;}vector<string> path;//答案路徑while(x!="0000") path.push_back(x),x=fa[x];path.push_back("0000");reverse(path.begin(), path.end());for(int i=0;i<path.size();i++){if(i!=0) printf("->");cout<<path[i];}printf("\n");}
}
int main()
{int t=1;//scanf("%d",&t);while(t--) solve();return 0;
}Chemical Equation
A?chemical equation?is the symbolic representation of a chemical reaction in the form of symbols and formulae, wherein the reactant entities are given on the left-hand side and the product entities on the right-hand side. For example,?CH4?+2O2?=CO2?+2H2?O?means that the reactants in this chemical reaction are methane and oxygen:?CH4??and?O2?, and the products of this reaction are carbon dioxide and water:?CO2??and?H2?O.
Given a set of reactants and products, you are supposed to tell that in which way we can obtain these products, provided that each reactant can be used only?once. For the sake of simplicity, we will consider all the entities on the right-hand side of the equation as one single product.
Input Specification:
Each input file contains one test case. For each case, the first line gives an integer?N?(2≤N≤20), followed by?N?distinct indices of reactants. The second line gives an integer?M?(1≤M≤10), followed by?M?distinct indices of products. The index of an entity is a 2-digit number.
Then a positive integer?K?(≤50) is given, followed by?K?lines of equations, in the format:
reactant_1 + reactant_2 + ... + reactant_n -> product
where all the reactants are distinct and are in increasing order of their indices.
Note: It is guaranteed that
- one set of reactants will not produce two or more different products, i.e. situation like?
01 + 02 -> 03?and?01 + 02 -> 04?is impossible; - a reactant cannot be its product unless it is the only one on the left-hand side, i.e.?
01 -> 01?is always true (no matter the equation is given or not), but?01 + 02 -> 01?is impossible; and - there are never more than 5 different ways of obtaining a product given in the equations list.
Output Specification:
For each case, print the equations that use the given reactants to obtain all the given products. Note that each reactant can be used only?once.
Each equation occupies a line, in the same format as we see in the inputs. The equations must be print in the same order as the products given in the input. For each product in order, if the solution is not unique, always print the one with the smallest sequence of reactants -- A sequence {?a1?,?,am??} is said to be smaller than another sequence {?b1?,?,bn??} if there exists?1≤i≤min(m,n)?so that?aj?=bj??for all?j<i, and?ai?<bi?.
It is guaranteed that at least one solution exists.
Sample Input:
8 09 05 03 04 02 01 16 10
3 08 03 04
6
03 + 09 -> 08
02 + 08 -> 04
02 + 04 -> 03
01 + 05 -> 03
01 + 09 + 16 -> 03
02 + 03 + 05 -> 08
Sample Output:
02 + 03 + 05 -> 08
01 + 09 + 16 -> 03
04 -> 04題意:給定n個反應物,m個要求生成物,k個反應方程式,自身可以直接等于反應物,每個反應物只能用一次,要求輸出能夠生產所有給定生成物的方程式,如果多條滿足,輸出參數最小的。
解析:數據小,DFS暴力每個方案,用map存下當前合成物所有的方程式,DFS前可以直接將生成物的所有方程式排序,這樣DFS找到的第一個可行方案就是答案。
#include <bits/stdc++.h>
using namespace std;
const int N=1e2+5;
int n,m,k;
map<int,vector<vector<int>>> mp;
int has[N],a[N],ans_id[N];//分別記錄是否存在該物質以及要求合成的物質
bool find_ans;
void dfs(int cnt)
{if(find_ans) return;if(cnt==m+1){find_ans=true;for(int i=1;i<=m;i++){int vl=a[i],id=ans_id[vl];vector<int> v=mp[vl][id];for(int j=0;j<v.size();j++){if(j!=0) printf(" + ");printf("%02d",v[j]);}printf(" -> %02d\n",vl);}return;}int vl=a[cnt];//當前需要合成的物質for(int i=0;i<mp[vl].size();i++){vector<int> v=mp[vl][i];bool ok=true;//判斷當前所需物質是否還有for(int j=0;j<v.size();j++){if(!has[v[j]]){ok=false;break;}}if(ok)//余料充足{for(int j=0;j<v.size();j++) has[v[j]]--;//使用這些物質ans_id[vl]=i;//物質vl使用第i個方案dfs(cnt+1);for(int j=0;j<v.size();j++) has[v[j]]++;//回溯}}
}
void solve()
{scanf("%d",&n);for(int i=1;i<=n;i++){int x;scanf("%d",&x);has[x]++;}scanf("%d",&m);for(int i=1;i<=m;i++) scanf("%d",&a[i]);scanf("%d",&k);getchar();//因為下面要getline,因此要吃掉scanf最后一個回車for(int i=1;i<=k;i++){string s;getline(cin,s);int sum=0;vector<int> v;for(int j=0;j<s.size();j++){if(s[j]==' '||s[j]=='-') continue;if(s[j]>='0'&&s[j]<='9') sum=sum*10+s[j]-'0';else v.push_back(sum),sum=0;}mp[sum].push_back(v);}for(int i=1;i<=m;i++){int vl=a[i];if(has[vl]) mp[vl].push_back({vl});//自身等于合成物sort(mp[vl].begin(),mp[vl].end());//每個合成物內部排序}dfs(1);
}
int main()
{int t=1;//scanf("%d",&t);while(t--) solve();return 0;
})


:能源行業應用)











(掃雷,灌溉,回文日期))
)


