本章我們來學習一下數據結構的排序算法！

目錄

1.排序的概念及其運用

1.1排序的概念

1.2?常見的排序算法

2.常見排序算法的實現

2.1 插入排序

2.1.1基本思想：

2.1.2直接插入排序：

2.1.3 希爾排序( 縮小增量排序 )

2.2 選擇排序

2.2.1基本思想：

2.2.2 直接選擇排序:

2.2.3 堆排序

2.3 交換排序

2.3.1冒泡排序

2.3.2 快速排序

1. hoare版本

2. 挖坑法

3. 前后指針版本??編輯

2.3.2 快速排序優化

?2.3.3?快速排序非遞歸

2.4 歸并排序

2.5 非比較排序

3.排序算法復雜度及穩定性分析

1.排序的概念及其運用

1.1排序的概念

（1）排序：所謂排序，就是使一串記錄，按照其中的某個或某些關鍵字的大小，遞增或遞減的排列起來的操作。

（2）穩定性：假定在待排序的記錄序列中，存在多個具有相同的關鍵字的記錄，若經過排序，這些記錄的相對次???序保持不變，即在原序列中，??r [ i ] = r?[ j ]，且?r [ i ]?在?r [ j ]?之前，而在排序后的序列中，??r [ i ]?仍在?r [ j ]之前，則稱這種排序算法是穩定的；否則稱為不穩定的。

（3）內部排序：數據元素全部放在內存中的排序。

（4）外部排序：數據元素太多不能同時放在內存中，根據排序過程的要求不能在內外存之間移動數據的排序。

1.2?常見的排序算法

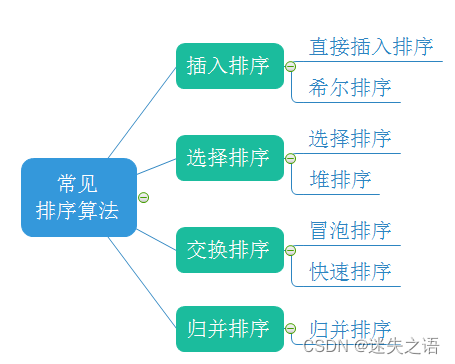
2.常見排序算法的實現

2.1 插入排序

2.1.1基本思想：

直接插入排序是一種簡單的插入排序法，其基本思想是：

????????把待排序的記錄按其關鍵碼值的大小逐個插入到一個已經排好序的有序序列中，直到所有的記錄插入完為止，得到一個新的有序序列 。

2.1.2直接插入排序：

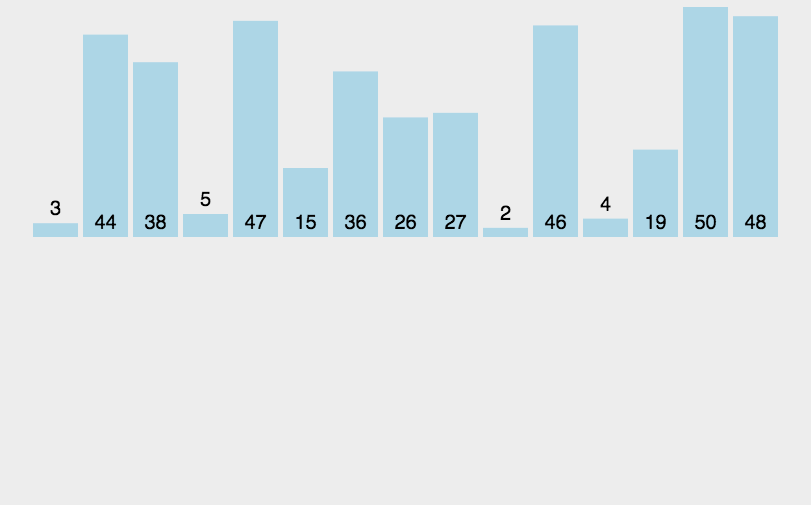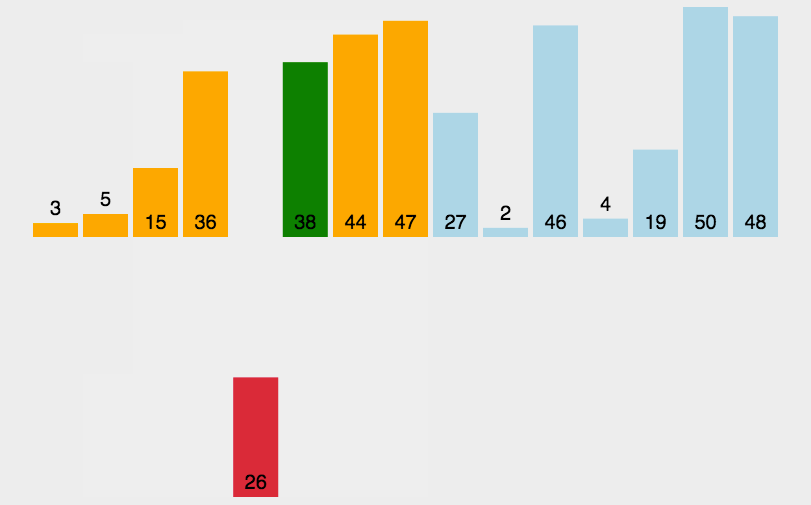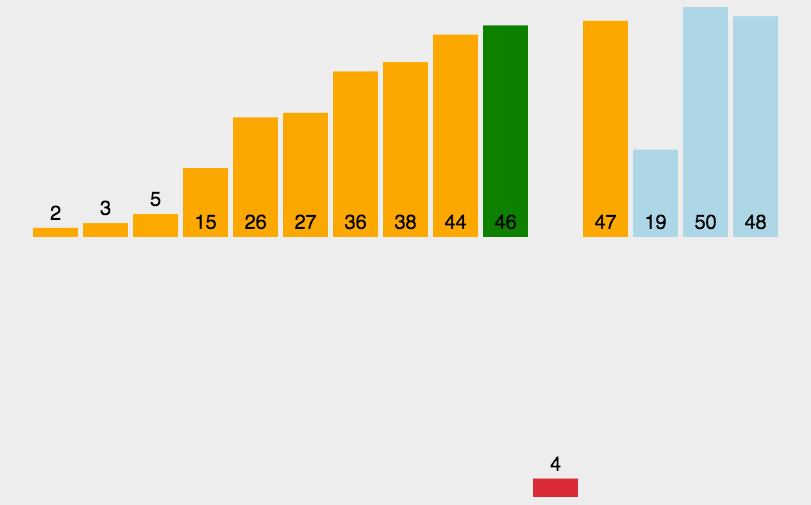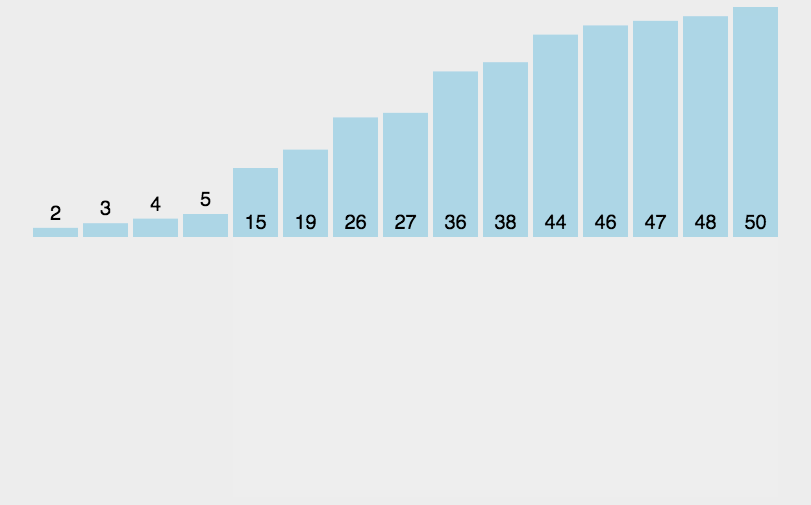
// 時間復雜度：O(N^2) 逆序
// 最好的情況：O(N)  順序有序
void InsertSort(int* a, int n)
{// [0, end] end+1for (int i = 0; i < n-1; ++i){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp > a[end]){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;}
}

直接插入排序的特性總結：

????????1. 元素集合越接近有序，直接插入排序算法的時間效率越高。

????????2. 時間復雜度： O(N^2)

????????3. 空間復雜度： O(1) ，它是一種穩定的排序算法。

????????4. 穩定性：穩定

2.1.3 希爾排序( 縮小增量排序 )

?

?代碼案例：

// 平均O(N^1.3)
void ShellSort(int* a, int n)
{int gap = n;// gap > 1時是預排序，目的讓他接近有序// gap == 1是直接插入排序，目的是讓他有序while (gap > 1){//gap = gap / 2;gap = gap / 3 + 1;for (int i = 0; i < n - gap; ++i){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}

希爾排序的特性總結：

????????1. 希爾排序是對直接插入排序的優化。

????????2. 當 gap > 1 時都是預排序，目的是讓數組更接近于有序。當 gap == 1 時，數組已經接近有序的了，這樣就會很快。這樣整體而言，可以達到優化的效果。我們實現后可以進行性能測試的對比。

????????3. 希爾排序的時間復雜度不好計算，因為 gap 的取值方法很多，導致很難去計算，因此在好些書中給出的希爾排序的時間復雜度都不固定：

《數據結構 (C 語言版 ) 》 --- 嚴蔚敏

?《數據結構-用面相對象方法與C++描述》--- 殷人昆

因為gap是按照Knuth提出的方式取值的，而且Knuth進行了大量的試驗統計，我們暫時就按照： 到? 來算。

????????4. 穩定性：不穩定

2.2 選擇排序

2.2.1基本思想：

2.2.2 直接選擇排序:

??代碼案例：

// 時間復雜度：O(N^2)
// 最好的情況下：O(N^2)
void SelectSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){int mini = begin, maxi = begin;for (int i = begin + 1; i <= end; ++i){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[begin], &a[mini]);if (maxi == begin){maxi = mini;}Swap(&a[end], &a[maxi]);++begin;--end;}
}

直接選擇排序的特性總結：

????????1. 直接選擇排序思考非常好理解，但是效率不是很好。實際中很少使用。

????????2. 時間復雜度： O(N^2)

????????3. 空間復雜度： O(1)

????????4. 穩定性：不穩定

2.2.3 堆排序

?

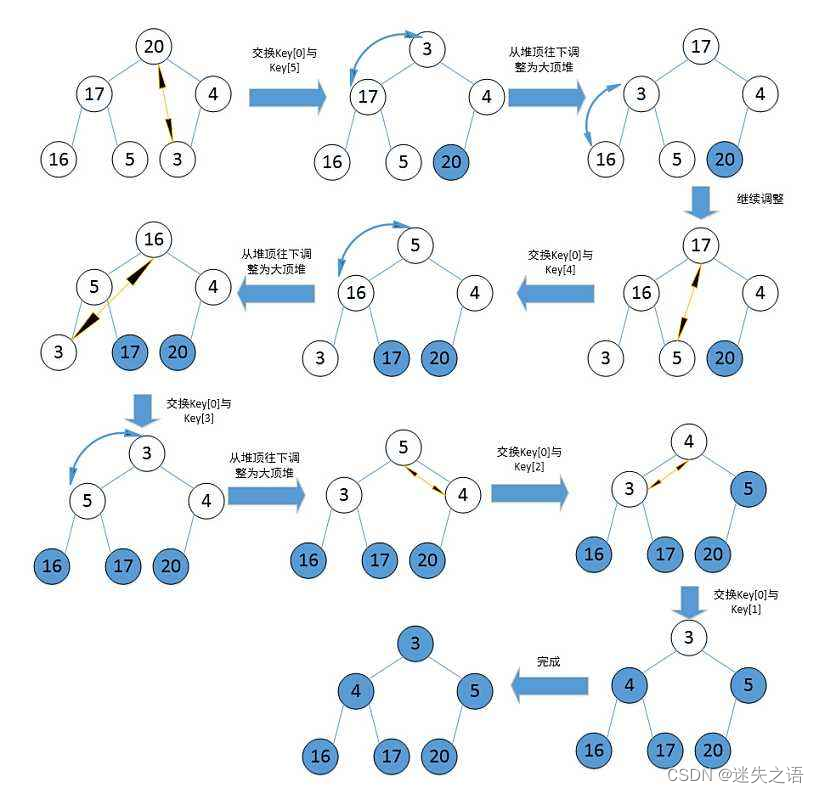
?代碼案例：

void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){// 假設左孩子小，如果解設錯了，更新一下if (child + 1 < size && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}// 升序
void HeapSort(int* a, int n)
{// O(N)// 建大堆for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}// O(N*logN)int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}

堆排序的特性總結：

????????1. 堆排序使用堆來選數，效率就高了很多。

????????2. 時間復雜度： O(N*logN)

????????3. 空間復雜度： O(1)

????????4. 穩定性：不穩定

2.3 交換排序

2.3.1冒泡排序

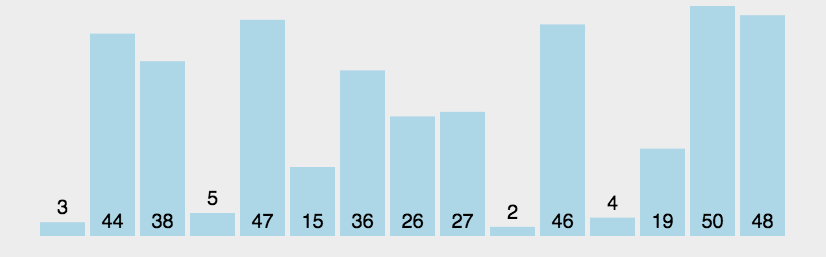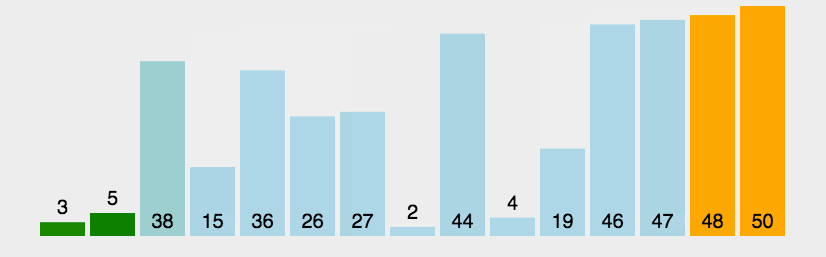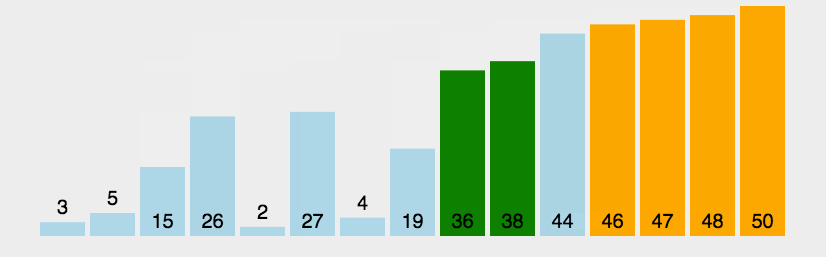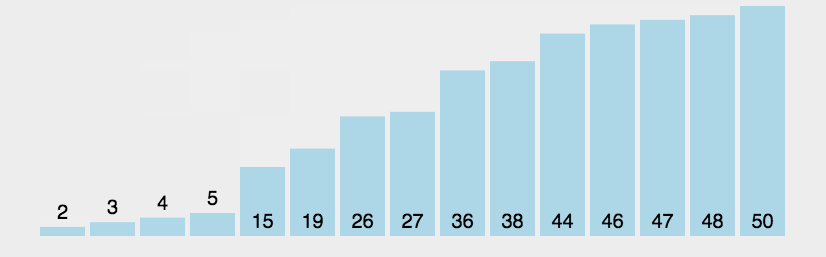
?代碼案例：

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// 時間復雜度：O(N^2)
// 最好情況是多少：O(N)
void BubbleSort(int* a, int n)
{for (int j = 0; j < n; j++){bool exchange = false;for (int i = 1; i < n-j; i++){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = true;}}if (exchange == false)break;}

冒泡排序的特性總結：

????????1. 冒泡排序是一種非常容易理解的排序

????????2. 時間復雜度： O(N^2)

????????3. 空間復雜度： O(1)

????????4. 穩定性：穩定

2.3.2 快速排序

?代碼案例：

// 假設按照升序對array數組中[left, right)區間中的元素進行排序
void QuickSort(int array[], int left, int right)
{if(right - left <= 1)return;// 按照基準值對array數組的 [left, right)區間中的元素進行劃分int div = partion(array, left, right);// 劃分成功后以div為邊界形成了左右兩部分 [left, div) 和 [div+1, right)// 遞歸排[left, div)QuickSort(array, left, div);// 遞歸排[div+1, right)QuickSort(array, div+1, right);
}int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;// begin end midi三個數選中位數if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else{//...}
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){// 右邊找小while (left < right && a[right] >= a[keyi]){--right;}// 左邊找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;// [begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}

1. hoare版本

代碼案例：

int PartSort1(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){// 右邊找小while (left < right && a[right] >= a[keyi]){--right;}// 左邊找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);return left;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort1(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}

2. 挖坑法

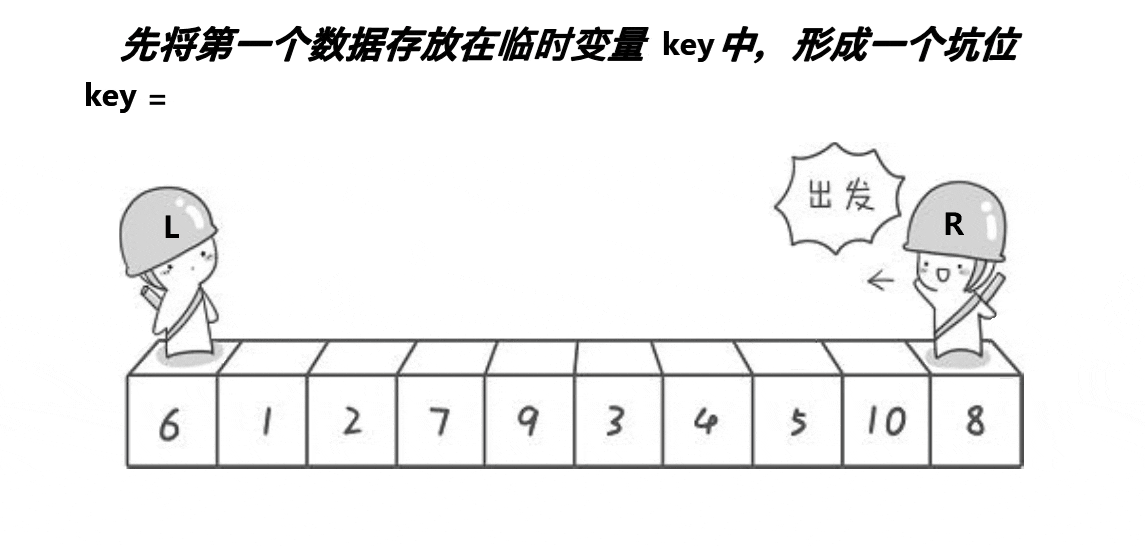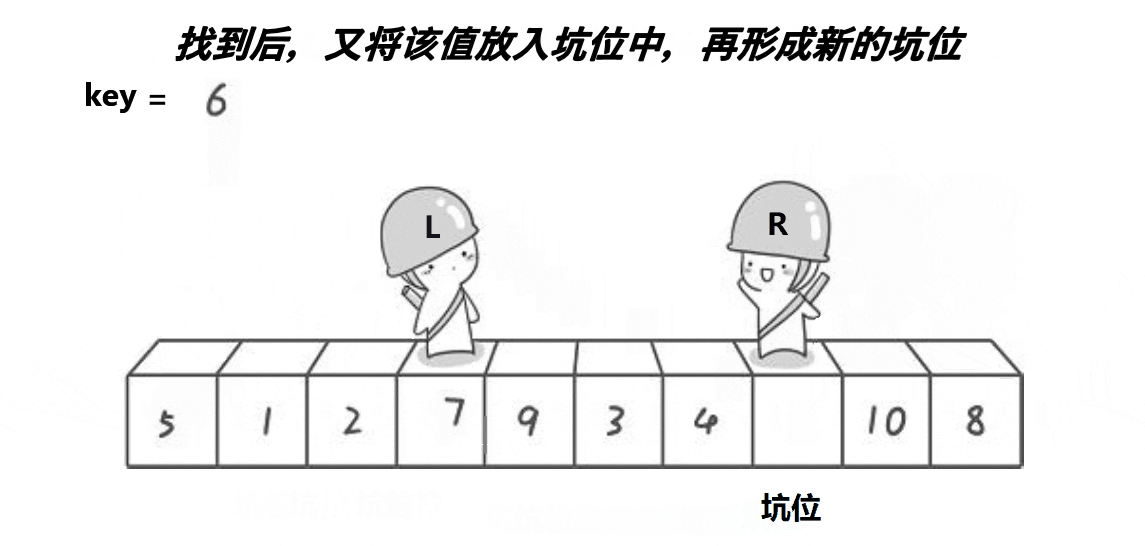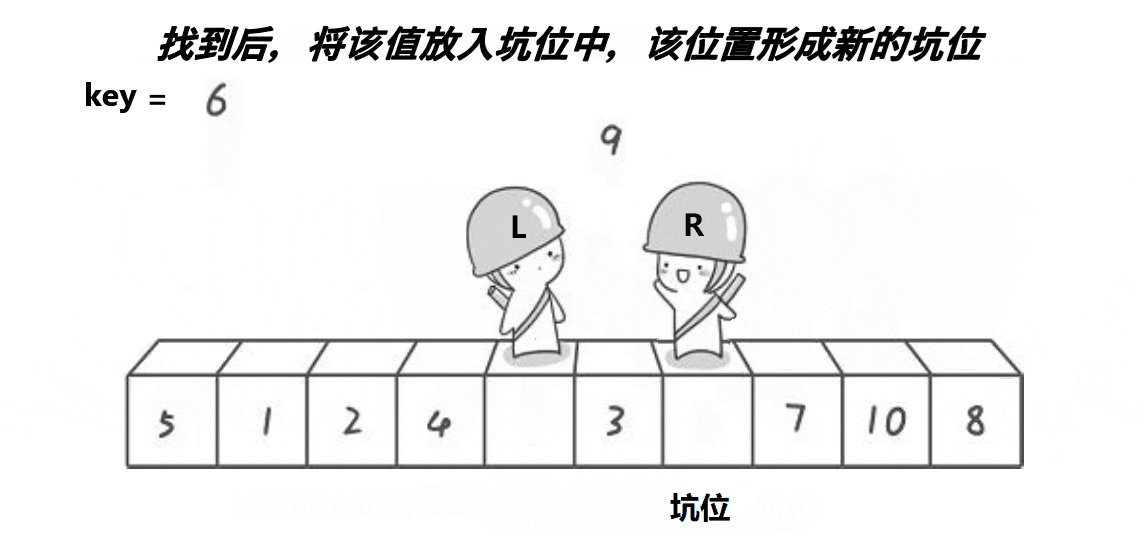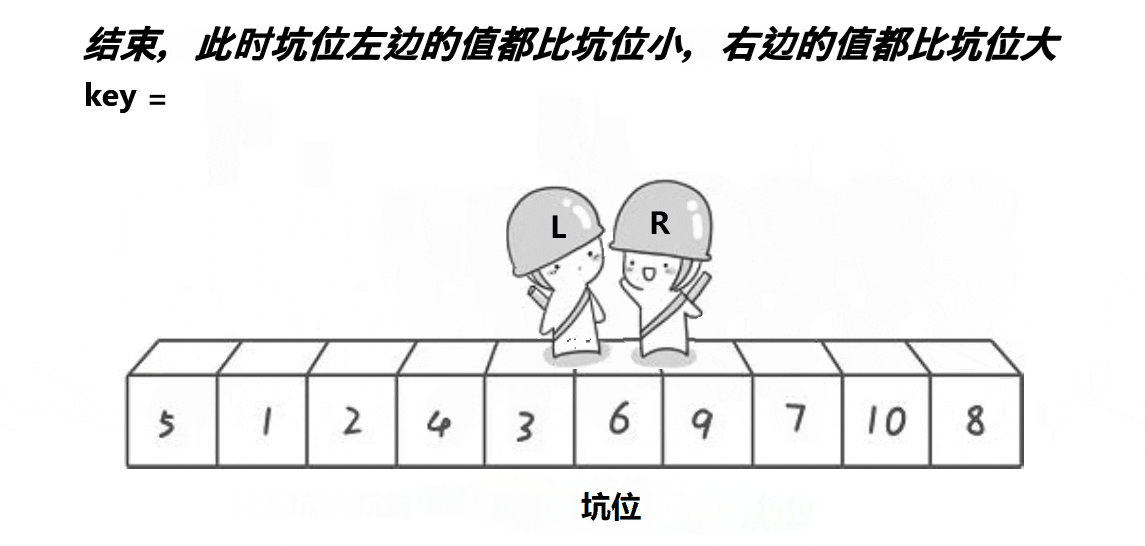
?代碼案例：

// 挖坑法
int PartSort2(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int key = a[begin];int hole = begin;while (begin < end){// 右邊找小，填到左邊的坑while (begin < end && a[end] >= key){--end;}a[hole] = a[end];hole = end;// 左邊找大，填到右邊的坑while (begin < end && a[begin] <= key){++begin;}a[hole] = a[begin];hole = begin;}a[hole] = key;return hole;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort2(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}

3. 前后指針版本?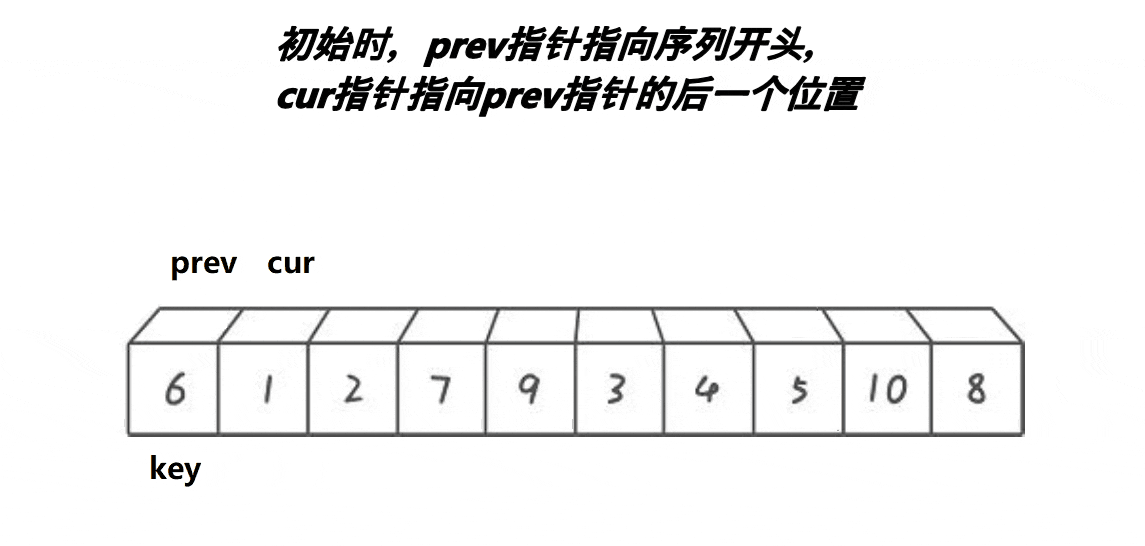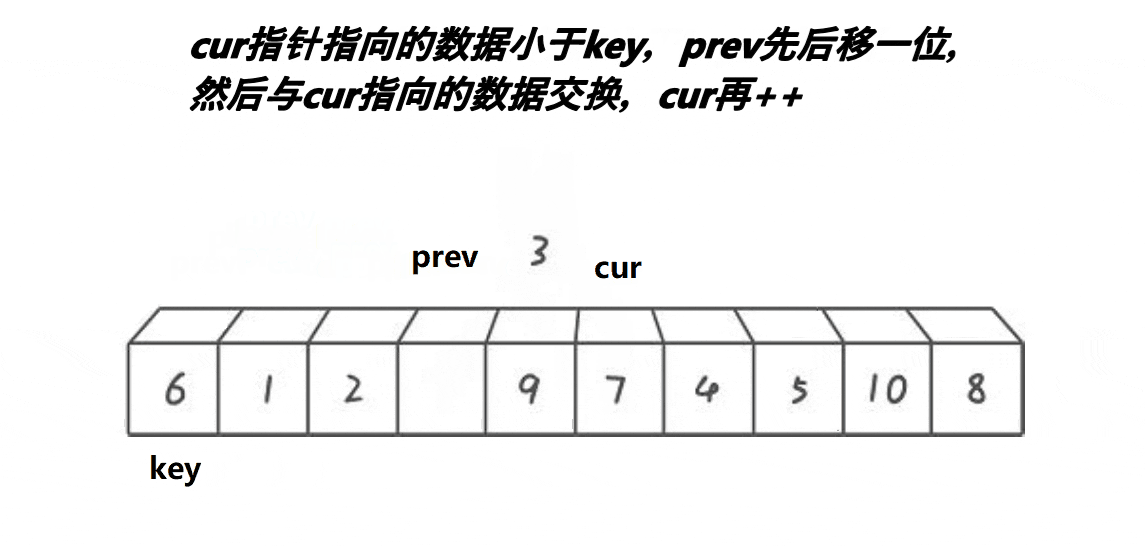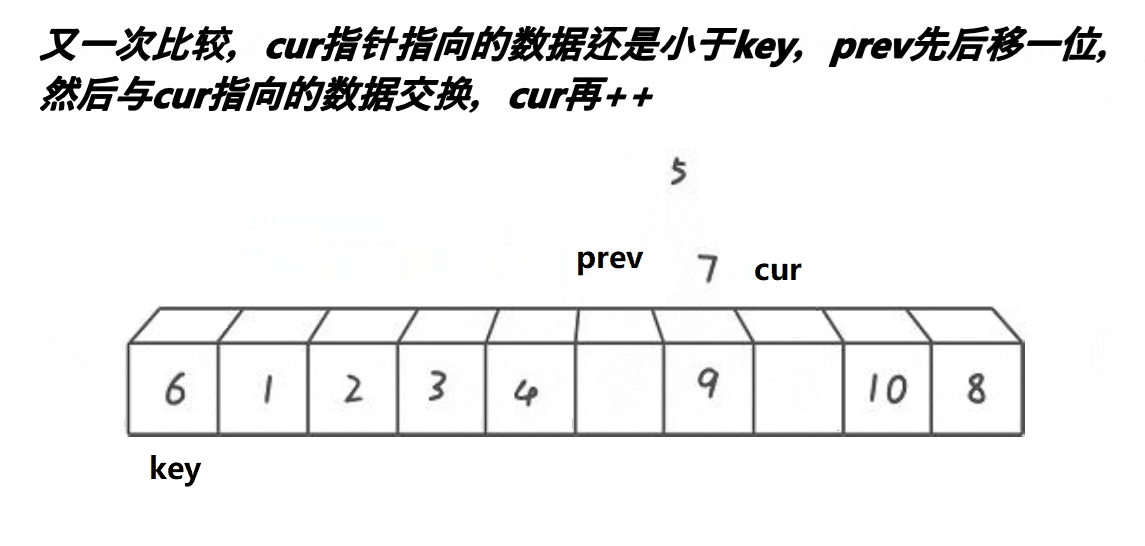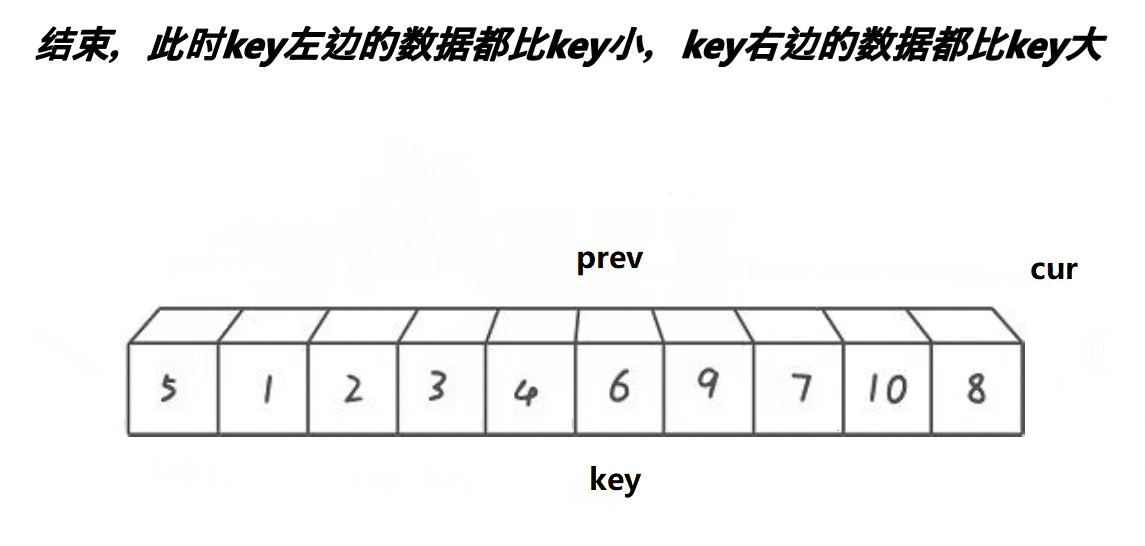

?代碼案例：

int PartSort3(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int keyi = begin;int prev = begin;int cur = prev + 1;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort3(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}

2.3.2 快速排序優化

1. 三數取中法選 key

2. 遞歸到小的子區間時，可以考慮使用插入排序

?2.3.3?快速排序非遞歸

?代碼案例：

void QuickSortNonR(int* a, int left, int right)
{Stack st;StackInit(&st);StackPush(&st, left);StackPush(&st, right);while (StackEmpty(&st) != 0){right = StackTop(&st);StackPop(&st);left = StackTop(&st);StackPop(&st);if(right - left <= 1)continue;int div = PartSort1(a, left, right);// 以基準值為分割點，形成左右兩部分：[left, div) 和 [div+1, right)StackPush(&st, div+1);StackPush(&st, right);StackPush(&st, left);StackPush(&st, div);}StackDestroy(&s);
}

快速排序的特性總結：

????????1. 快速排序整體的綜合性能和使用場景都是比較好的，所以才敢叫 快速 排序

????????2. 時間復雜度： O(N*logN)

3. 空間復雜度： O(logN)

4. 穩定性：不穩定

2.4 歸并排序

基本思想：

????????歸并排序（MERGE-SORT ）是建立在歸并操作上的一種有效的排序算法 , 該算法是采用分治法（ Divide and Conquer）的一個非常典型的應用。將已有序的子序列合并，得到完全有序的序列；即先使每個子序列有序，再使子序列段間有序。若將兩個有序表合并成一個有序表，稱為二路歸并。 歸并排序核心步驟：

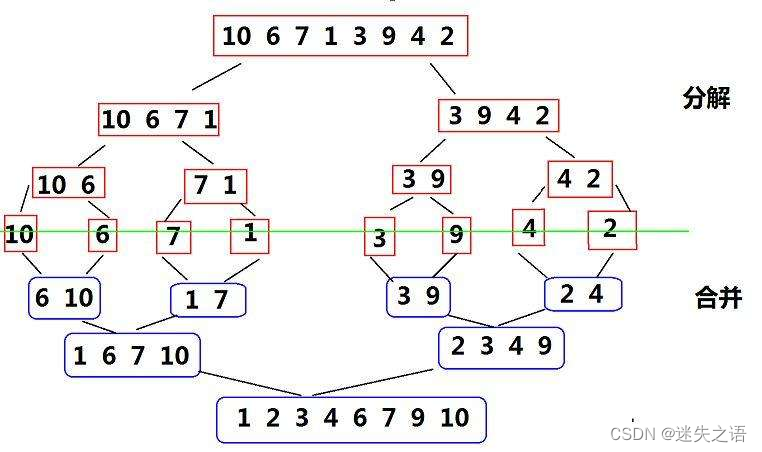
??代碼案例：

void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin >= end)return;int mid = (begin + end) / 2;// [begin, mid][mid+1, end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid+1, end, tmp);// [begin, mid][mid+1, end]歸并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while(begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp);
}//非遞歸法
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){printf("gap:%2d->", gap);for (size_t i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;// [begin1, end1][begin2, end2] 歸并//printf("[%2d,%2d][%2d, %2d] ", begin1, end1, begin2, end2);// 邊界的處理if (end1 >= n || begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}//printf("[%2d,%2d][%2d, %2d] ", begin1, end1, begin2, end2);int j = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2-i+1));}printf("\n");gap *= 2;}free(tmp);
}

歸并排序的特性總結：

????????1. 歸并的缺點在于需要 O(N) 的空間復雜度，歸并排序的思考更多的是解決在磁盤中的外排序問題。

????????2. 時間復雜度： O(N*logN)

????????3. 空間復雜度： O(N)

????????4. 穩定性：穩定

2.5 非比較排序

思想：計數排序又稱為鴿巢原理，是對哈希直接定址法的變形應用。 操作步驟：

????????1. 統計相同元素出現次數

????????2. 根據統計的結果將序列回收到原來的序列中

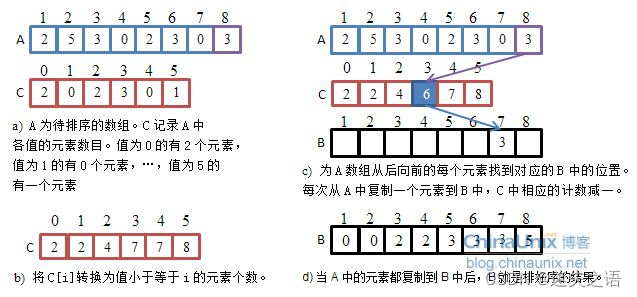
?代碼案例：

// 基數排序/桶排序// 計數排序
// 時間：O(N+range)
// 空間：O(range)
void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (int i = 1; i < n; i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}int range = max - min + 1;int* count = (int*)calloc(range, sizeof(int));if (count == NULL){printf("calloc fail\n");return;}// 統計次數for (int i = 0; i < n; i++){count[a[i] - min]++;}// 排序int i = 0;for (int j = 0; j < range; j++){while (count[j]--){a[i++] = j + min;}}
}

計數排序的特性總結：

????????1. 計數排序在數據范圍集中時，效率很高，但是適用范圍及場景有限。

????????2. 時間復雜度： O(MAX(N, 范圍 ))

????????3. 空間復雜度： O( 范圍 )

????????4. 穩定性：穩定

3.排序算法復雜度及穩定性分析

?

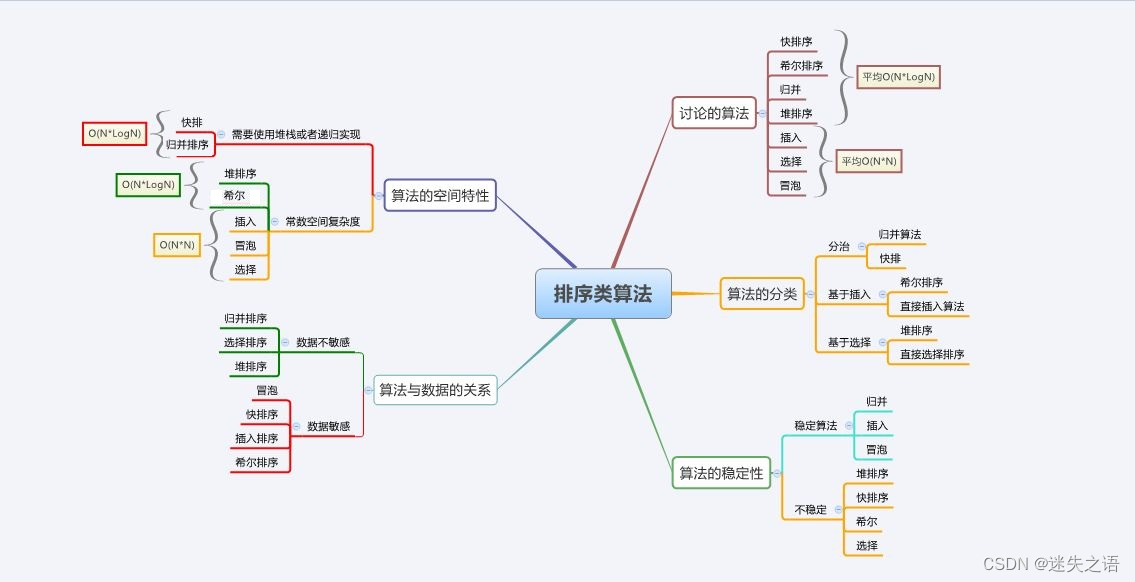
?注：

? ? ? ? （1）算法穩定性是指，待排序列中相同的值在排序后相對順序不變，這就是算法穩定。

????????（2）輔助空間是指在排序的過程中開辟了新的空間。

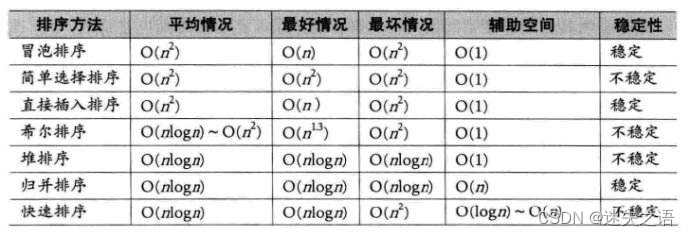
?本篇完！