像素
- 像素是分辨率的單位;
- 構成位圖圖像的最基本單元;
- 每個像素都有自己的顏色;
圖像分辨率
- 單位英寸內的像素點數;
- 單位為PPI(Pixels?Per?Inch),為像素每英寸;
- PPI表示每英寸對角線上所擁有的像素數目:
,x:長度像素數目,y:寬度像素數目,Z:屏幕大小;
- 屏幕尺寸(大小)指的是對角線長度;
- 圖像清晰度的評價指標;
顏色模型
- 色彩三原色(CMYK):品紅,黃,青;
- 光學三原色(RGB):紅\綠\藍;

RGB模型?
- 三維直角坐標顏色系統中的一個單位正方體;
- 正方體的主對角線上,各原色的量相等;
- 產生由暗到亮的白色,即灰度;
- 正方體的其他六個角點分別為紅\黃\綠\青\藍\品紅;

灰度
- 表示圖像像素明暗程度的數值;
- 黑白圖像中點的顏色深度;
- 范圍一般為0~255;
- 白色為255,黑色為0;
通道
- 把圖像分解成一個或多個顏色成分;
單通道
- 一個像素點只需一個數值表示;
- 只能表示灰度;
- 0為黑色,255為白色;
- 可表示二值圖/灰度圖;
三通道
- RGB模式;
- 把圖像分為紅\綠\藍三個通道;
- 可以表示彩色;
- 全0表示黑色;
四通道
- RGBA模式;
- 在RGB的基礎上加上alpha通道,表示透明度;
- alpha=0表示全透明;
對比度
- 不同顏色之間的差別;
- 對比度=最大灰度值/最小灰度值;
RGB轉為Gray
- 浮點算法:
;
- 整數算法:
;
- 移位算法:
;
- 平均值閥:
;
- 僅取綠色:
;
RGB值轉化為浮點數
- 浮點運算結果更精確;
- 整數運算中會丟失小數部分;
- 導致顏色值嚴重失真;
- 計算過程越多,失真越嚴重;
- 將RGB值轉化為[0,1]浮點數:x/255即可;
二值化
- 閾值隨意設置;
if(img_gray[i,j]<=0.5):img_gray[i,j]=0
else:img_gray[i,j]=1通用概念(庫的安裝和使用)
- 使用pip或者conda安裝;
- 百度搜索python?安裝xxx;
- 得到庫的名稱;
- 使用的時候用import引入;
- 不需要死記硬背函數;
- 需要使用的時候搜索函數名;
- 可了解函數用法和參數含義;
常用視覺庫
- opencv:安裝使用pip install opencv-python,使用時:import?cv2
- matplotlib:安裝使用pip?install?matplotlib,使用時:import?matplotlib.pyplot?as?plt
- skimage:安裝使用pip?install?scikit-image,使用時:import?skimage;
opencv?BGR
- opencv讀進來的圖片通道排列:B--G--R;
- 不是主流的R--G--B;
#opencv讀入的矩陣時BGR,想轉為RGB,可以這樣:
img=cv2.imread('1.jpg')
img=cv2.cvtColor(img,cv2.COLOR_BGR2RGB)圖像頻率
- 灰度值變化劇烈程度的指標;
- 是灰度在平面空間上的梯度;
圖像幅值
- 在一個周期內;
- 交流電瞬時出現的最大絕對值;
- 也是一個正弦波;波峰到波谷距離的一半;
數字圖像
- 計算機保存的圖像都是一個個像素點,稱為數字圖像;
圖像數字化過程
- 由圖像的取樣與量化來完成;
圖像的取樣
- 取樣就是決定用多少點來描述一幅圖像;
- 取樣結果質量的好壞用圖像的分辨率來衡量;
- 數字化坐標值稱為取樣;
- 若橫向的像素數(列數)為M,縱向的像素數(行數)為N;
- 圖像的總像素數為MxN個像素;
圖像的量化
- 指要用多大范圍的數值表示圖像采樣之后的一個點;
- 數字化圖像的幅度值稱為量化;
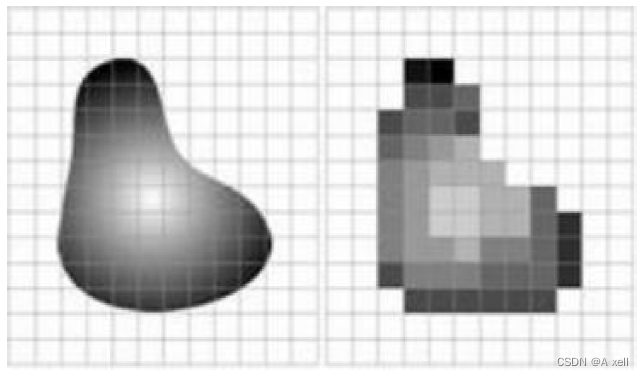
上采樣
- 放大圖像,或稱上采樣:upsampling或圖像插值:interpolating;
- 放大原圖像;
- 可將圖像顯示在更高分辨率的顯示設備上;
下采樣
- 縮小圖像,或稱下采樣:subsampled,或降采樣:downsampled;
- 使圖像符合顯示區域的大小;
- 生成對應圖像的縮率圖;
上采樣原理
- 內插值
下采樣原理
常用的插值方法
- 最臨近插值;
- 單線性插值;
- 雙線性插值;
最臨近插值
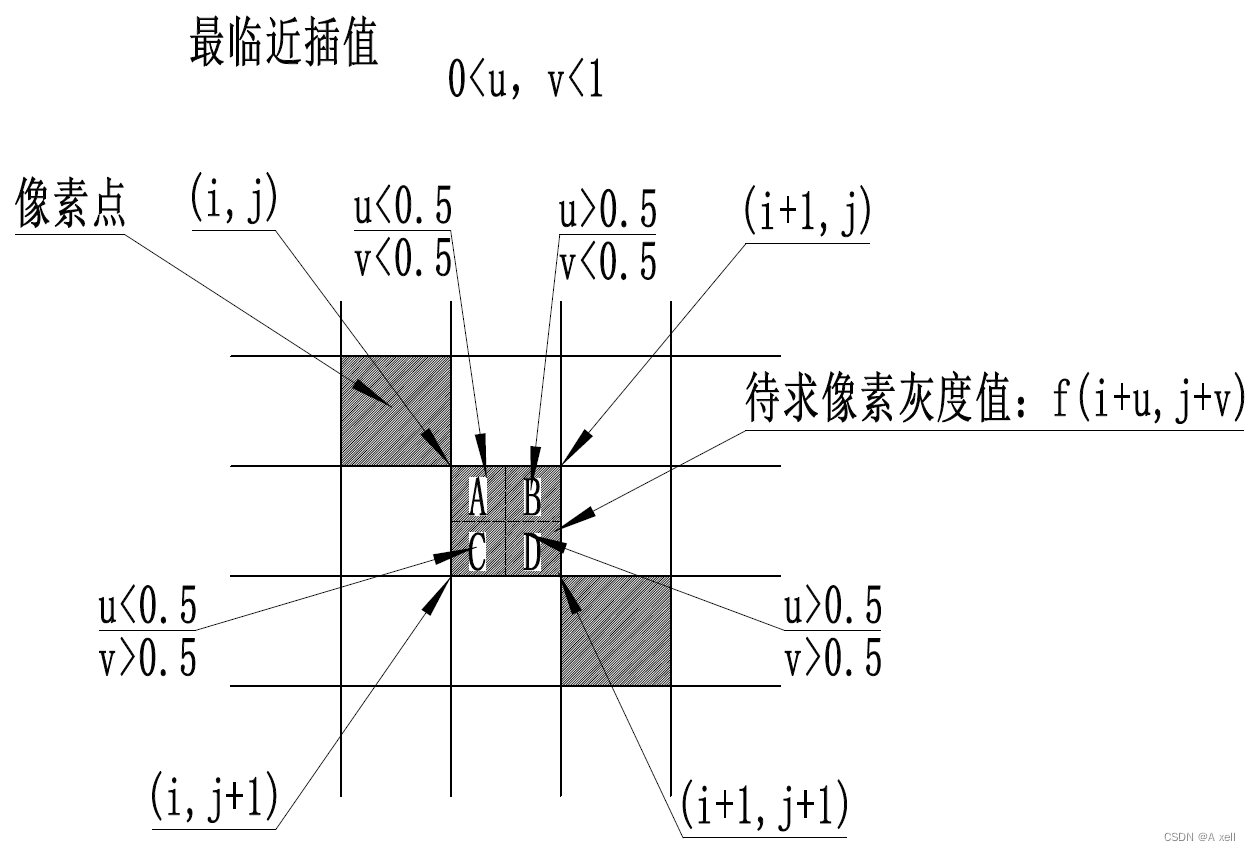
- The?nearest?interpolation;
- i+u,j+v為待求像素坐標;
- i,j為整數,u,v為大于零小于1的小數;
- 待求像素灰度值表示為f(i+u,j+v);
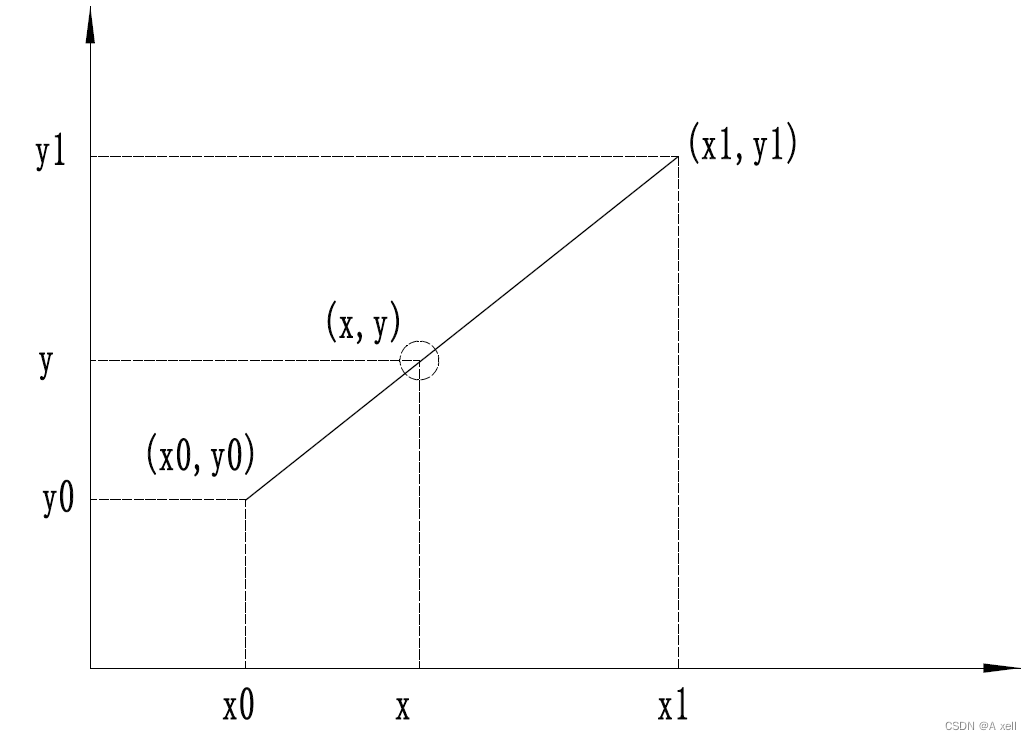
單線性插值
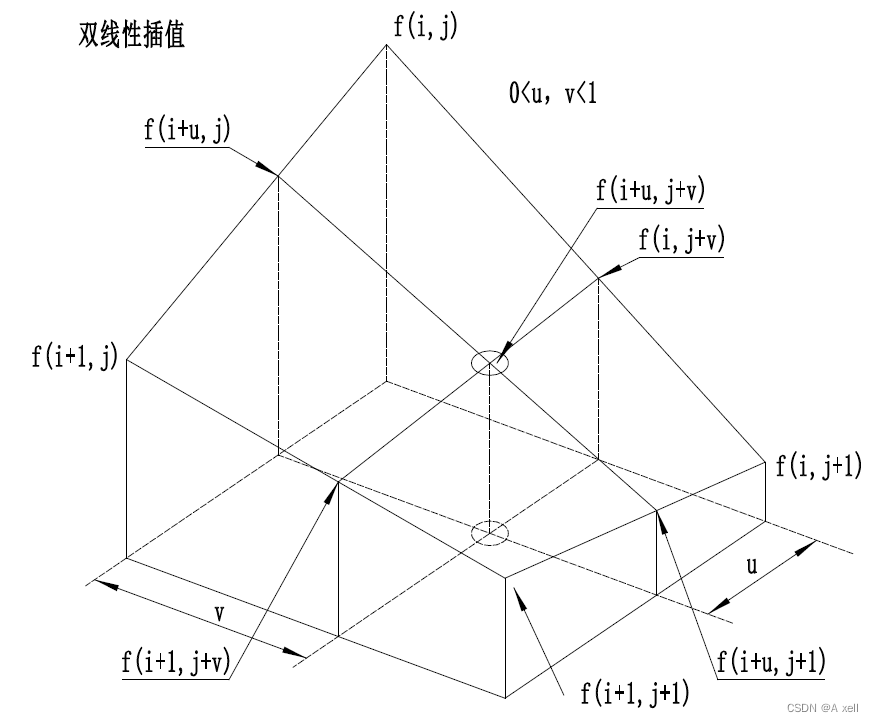
雙線性插值
????????????????????????????????
??????????????????????????????????????????????
?????????????????????????????????????????????????????
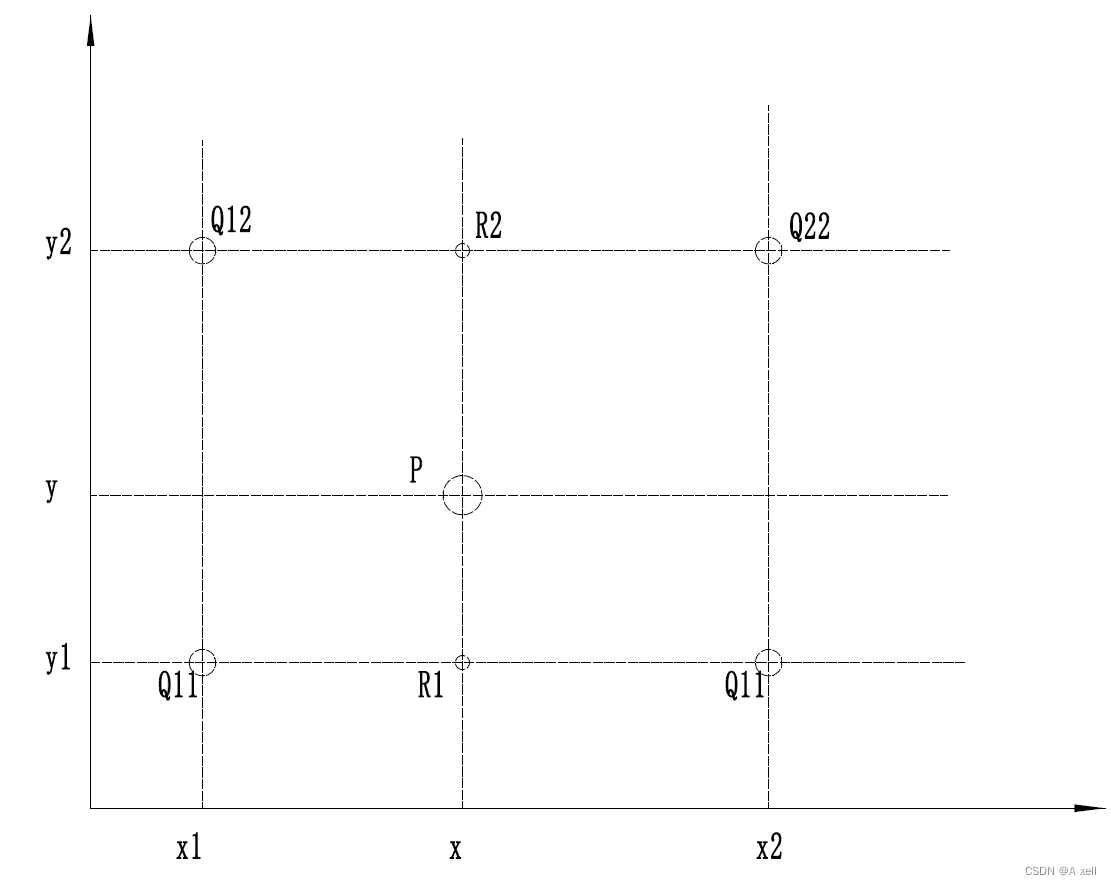
- 在x方向做插值:
- 在y方向作插值:
- 綜合起來
- 圖像雙線性插值只用相鄰的4個點,上述公式的分母都為1;
雙線性插值坐標系的選擇
- dst像素點的坐標對應到src圖像當中的坐標;
- 通過雙線性插值的方法算出src中相應坐標的像素值;
坐標對應關系
- 按比例對應:
源圖像和目標圖像的左上角對齊
- 如果源圖像和目標圖像的原點(0,0)均選擇左上角;
- 根據插值公式計算目標圖像每點像素;
- 假設需要將一幅5x5圖像縮小為3x3;
- 源圖像和目標圖像各像素之間的對應關系如下圖:

?源圖像和目標圖像的中心對齊
- 兩個圖像的幾何中心重合;
- 目標圖像的每個像素之間等間隔;
- 目標圖像的四邊和源圖像都有一定的邊距;
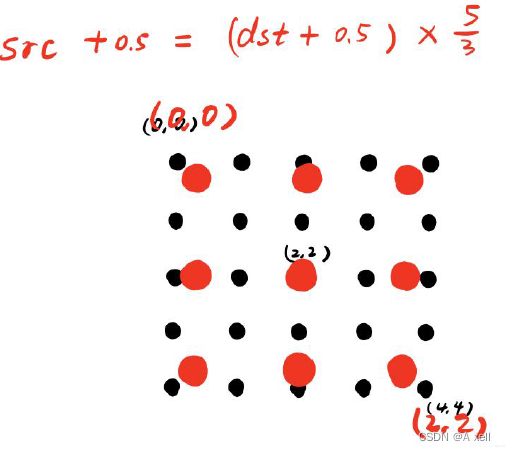
源圖像和目標圖像中心對齊平移參數的證明

雙線性插值存在的問題
- 雙線新插值較最臨近插值算法復雜;
- 計算量較大;
- 但是沒有灰度不連續的缺點;
- 圖像看起來更光滑;
直方圖
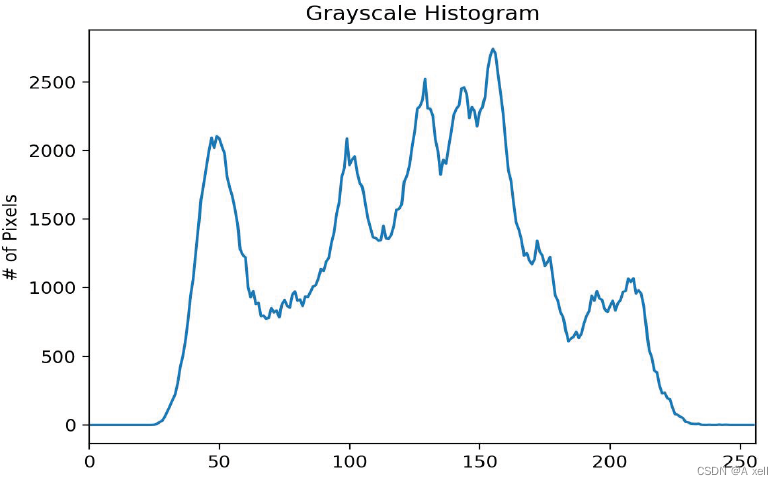
- 圖像處理中,經常用到直方圖:如顏色直方圖,灰度直方圖;
- 灰度直方圖描述了圖像中灰度分布的情況;
- 能夠直觀展示圖像中各灰度級所占比例;
- 灰度直方圖是灰度級的函數;
- 描述圖像中該灰度級的像素的個數;
- 直方圖中橫坐標是灰度級;
- 縱坐標是該灰度級出現的頻率;
直方圖的性質
- 反映圖像中的灰度分布規律;
- 描述每個灰度級具有的像素個數;
- 不包含像素在圖像中的位置信息;
- 不關心像素所處的空間位置;
- 不受圖像旋轉和平移變化的影響;
- 可以作為圖像的特征;
- 任何圖像都有唯一的直方圖對應;
- 不同的圖像可以有相同的直方圖;
- 如果一幅圖像有兩個不相連的區域組成;
- 每個區域的直方圖已知;
- 整幅圖像的直方圖是該兩個區域的直方圖之和;
直方圖的應用
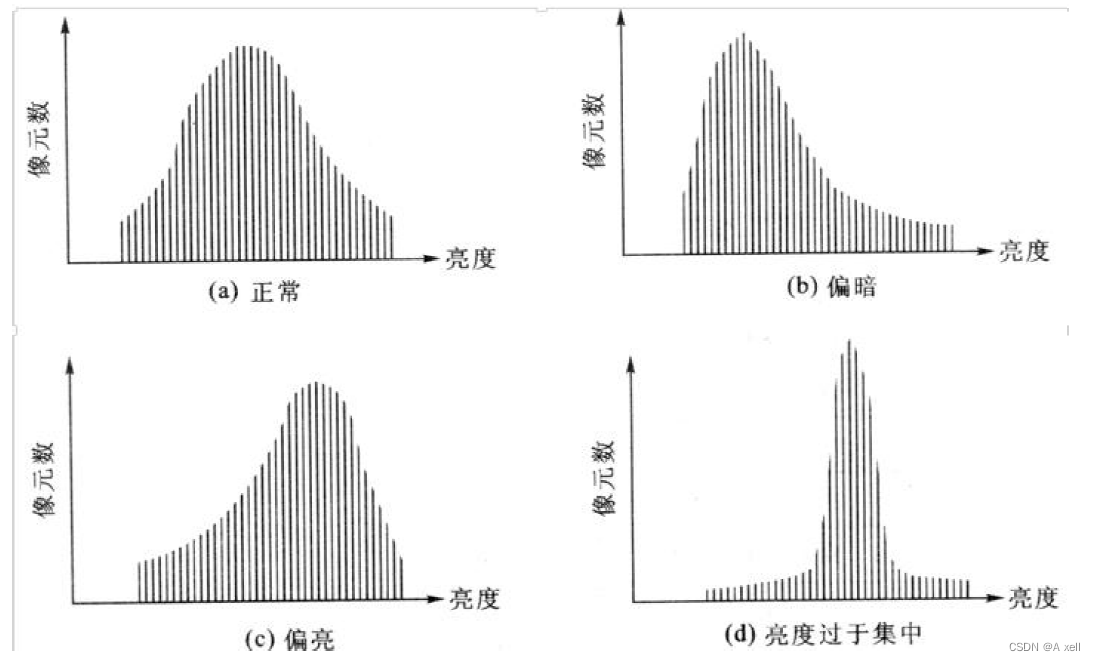
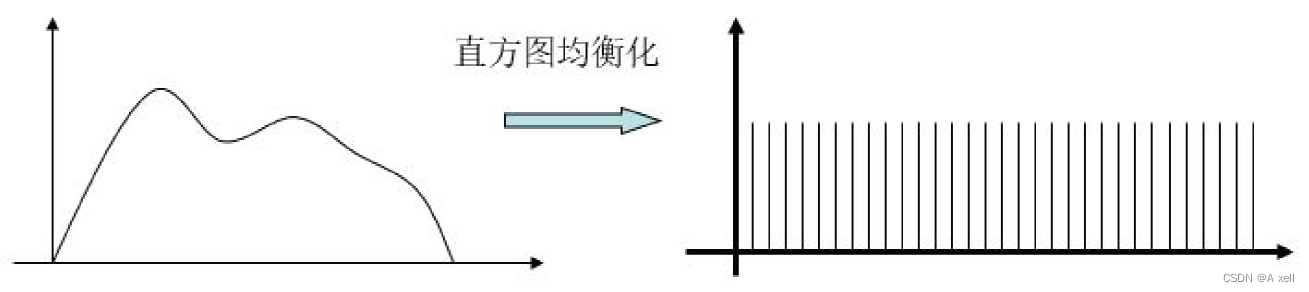
直方圖均衡化
- 將源圖像的直方圖變換為均勻的直方圖;
- 按均勻直方圖修改原圖像;
- 獲得灰度分布均勻的新圖像;
- 是用一定的算法使直方圖大致平和的方法;
- 作用是圖像增強;
直方圖均衡化的應用考慮
- 為了將原圖像的亮度范圍擴展;
- 需要一個映射函數;
- 將原圖像的像素值均衡映射到新直方圖中;
- 映射函數需要滿足:
- 不打亂原有的亮暗布局;
- 映射后亮\暗的關系不改變;
- 且映射后必須在原有的范圍內,比如(0-255);
直方圖均衡化的步驟
- 依次掃描原始灰度圖像的每一個像素;
- 計算出圖像的灰度直方圖H;
- 計算灰度直方圖的累加直方圖;
- 根據累加直方圖和直方圖均衡化的原理;
- 得出輸入與輸出之間的映射關系;
- 最后根據映射關系得出結果:
直方圖均衡化的計算原理
- 輸入圖像的任意一個像素p,
;
- 總能在輸出圖像中有對應的像素q,
;
- 滿足輸入和輸出的像素總量相等;
- 計算公式為(累加直方圖公式):
- 輸出圖像每個灰度級的個數為:
- 代入累加直方圖公式:
直方圖均衡化實例
- 原圖像矩陣,image:5x5,最大像素值max=9,最小像素值min=0;
| 1 | 3 | 9 | 9 | 8 |
| 2 | 1 | 3 | 7 | 3 |
| 3 | 6 | 0 | 6 | 4 |
| 6 | 8 | 2 | 0 | 5 |
| 2 | 9 | 2 | 6 | 0 |
- 直方圖均衡化計算表格:
| 像素值 | 該像素 值數量 | 該像素值占圖片 總像素值數量百分比: | 百分比 加合 | 四舍 五入 | |
| 0 | 3 | 3/25=0.12 | 0.12 | 29.72 | 30 |
| 1 | 2 | 2/25=0.08 | 0.2 | 50.2 | 50 |
| 2 | 4 | 0.16 | 0.36 | 91.16 | 91 |
| 3 | 4 | 0.16 | 0.52 | 132.12 | 132 |
| 4 | 1 | 0.04 | 0.56 | 142.36 | 142 |
| 5 | 1 | 0.04 | 0.6 | 152.6 | 153 |
| 6 | 4 | 0.16 | 0.76 | 193.56 | 194 |
| 7 | 1 | 0.04 | 0.8 | 203.8 | 204 |
| 8 | 2 | 0.08 | 0.88 | 224.28 | 224 |
| 9 | 3 | 0.12 | 1 | 255 | 255 |
- 目標圖像矩陣
| 50 | 132 | 255 | 255 | 224 |
| 91 | 50 | 132 | 204 | 132 |
| 132 | 194 | 30 | 194 | 142 |
| 194 | 224 | 91 | 30 | 153 |
| 92 | 255 | 91 | 194 | 30 |
線性濾波
- 是圖像處理的最基本方法;
- 允許對圖像進行處理,產生很多不同效果;
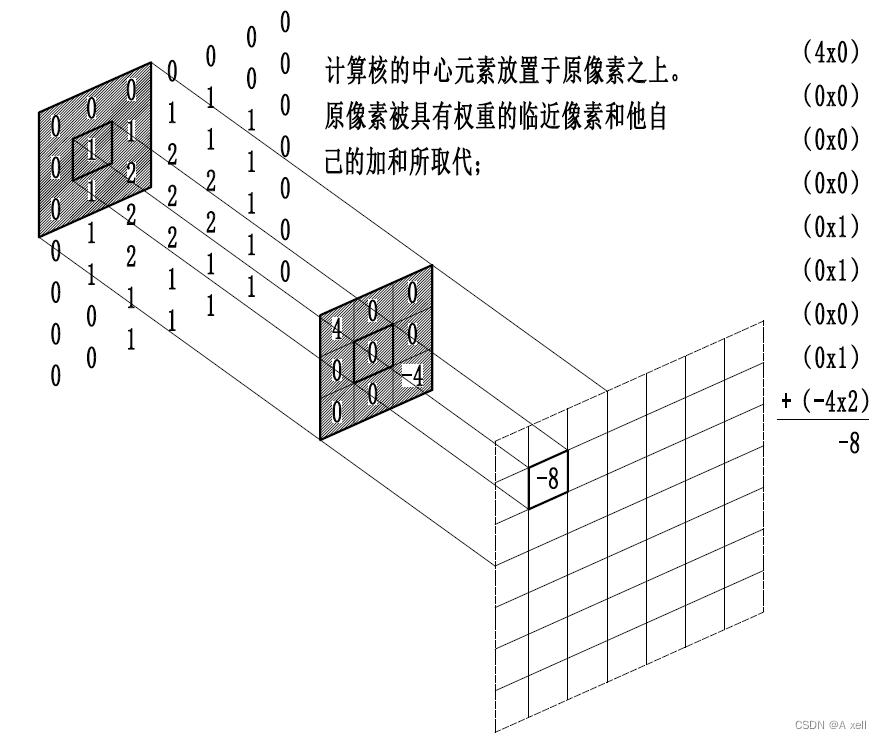
卷積
- 數學定義:
;
- g稱為作用在f上的過濾器(filter)或者核(kernel);
過濾器/卷積核的要求
- 大小應為奇數;
- 奇數才有一個中心,比如3x3,5x5或者7x7;
- 有中心才有半徑,比如,5x5的核半徑為2;
- 濾波器矩陣所有元素之和應該等于1;
- 這樣的核保證濾波前后圖像的亮度保持不變;
- 但不是硬性要求;
- 如果濾波器所有矩陣的元素之和大于1;
- 濾波后的圖像會比原圖像更亮;
- 如果濾波器所有矩陣元素之和小于1;
- 濾波后的圖像會比原圖像更暗;
- 如果濾波器矩陣的所有元素和為0;
- 圖像不會變黑,但會非常暗;
- 濾波后的圖像像素值可能會出現負數或者大于255的情況;
- 大于255的直接截斷;
- 負數取絕對值;
- 具體應用中的多卷積核;
- 認為每個卷積核代表一種圖像模式;
- 圖像與卷積核卷積出的值較大,說明圖像值接近卷積核;
- 假設我們設計了6個卷積核;
- 可以理解,我們認為該圖像上有6種底層紋理模式;
- 也就是我們使用6種基礎模式能描繪一幅圖像;
沒有任何效果的卷積
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
- 原像素中間像素值乘1;
- 其余像素全部乘以0;
- 像素值不會發生任何變化;
平劃均值濾波
| 1/9 | 1/9 | 1/9 |
| 1/9 | 1/9 | 1/9 |
| 1/9 | 1/9 | 1/9 |
- 取九個值的平均值代替中間像素值;
- 可以起到平滑的效果;
高斯平滑
| 1/16 | 2/16 | 1/16 |
| 2/16 | 2/16 | 2/16 |
| 1/16 | 2/16 | 1/16 |
- 高斯平滑水平和垂直方向呈現高斯分布;
- 突出了中心點在像素平滑后的權重;
- 相較于均值濾波,有更好的平滑效果;
圖像銳化
| -1 | -1 | -1 |
| -1 | 9 | -1 |
| -1 | -1 | -1 |
?
| 0 | -1 | 0 |
| -1 | 5 | -1 |
| 0 | -1 | 0 |
- 圖像銳化使用拉普拉斯變換核函數;
邊緣檢測
,

- 使用
卷積上圖;
- 會在圖像中間黑白邊界處獲得比較大的值;
Sobel邊緣檢測
- 水平梯度卷積核
| -1 | 0 | 1 |
| -2 | 0 | 2 |
| -1 | 0 | 1 |
- 垂直梯度卷積核
| -1 | -2 | -1 |
| 0 | 0 | 0 |
| 1 | 2 | 1 |
- ?Sobel更強調和邊緣相鄰的像素點對邊緣的影響;
卷積解決的問題
- 卷積負責提取圖像中的局部特征
卷積--步長/stride
- 卷積核的尺寸
;
- 圖片的尺寸
;
- 用卷積核來卷積圖片;
- 每次移動一個像素;
- 輸出結果的尺寸為:
;
- 如果每次移動不止一個像素,而是s個;
- 輸出結果的尺寸為:
;
- s稱為卷積步長/stride;
- 如果f或s的值比1大;
- 每次卷積之后結果的長寬,比卷積前小一些;
- 會丟失信息;
填充/padding
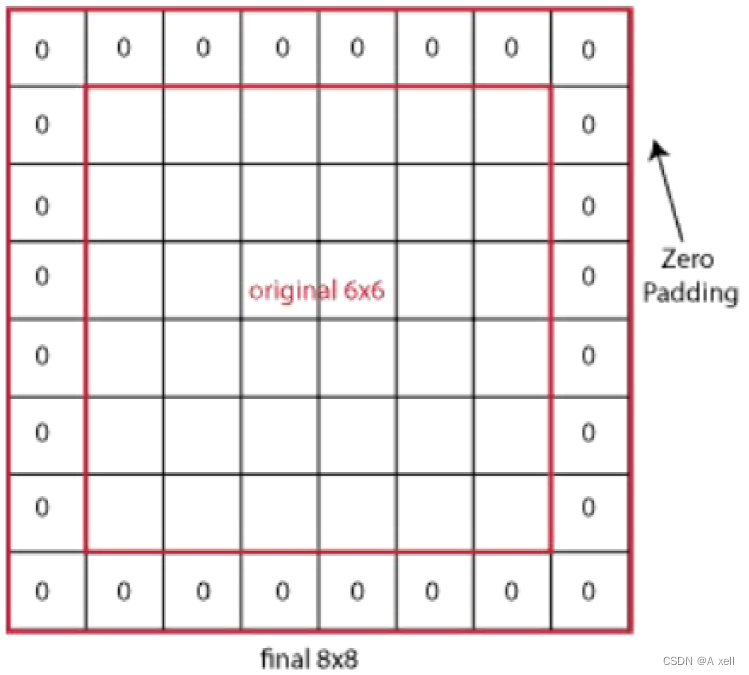
- 填充后,做卷積后的圖像大小:
- 如果想讓高(寬)不變:
- 假設步長s=1:
三種填充模式
- 橙色部分為圖像/image;
- 藍色部分為Filter/過濾器;
- 三種填充模式分別是full/same/valid;
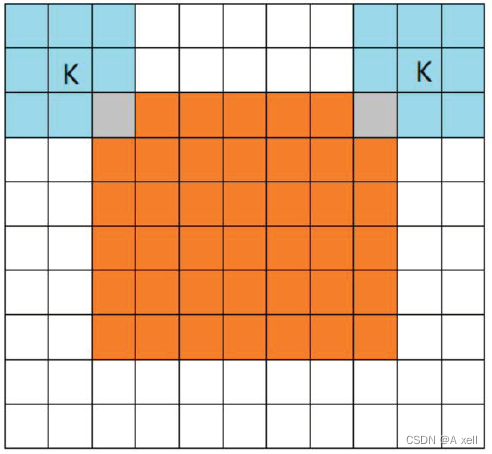
- 從filter和image剛相交開始做卷積.
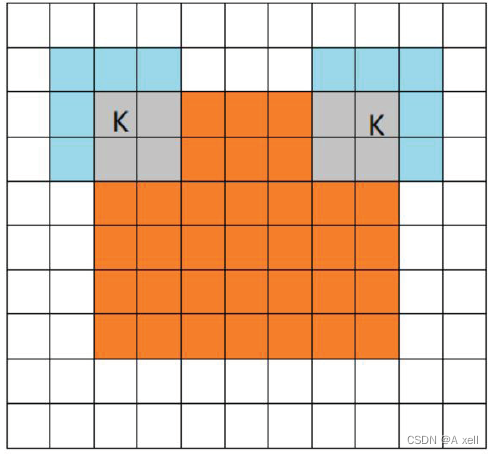
- filter中心(k)與image的邊角重合,開始卷積;?
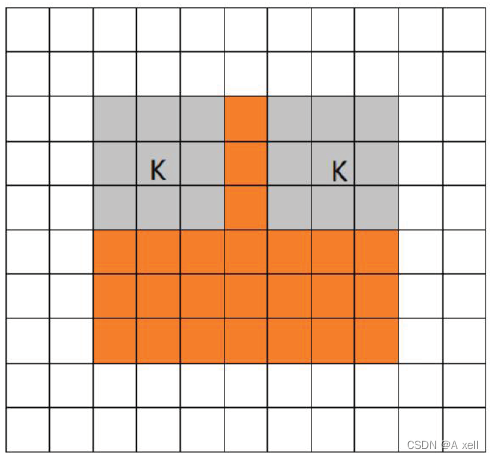
- filter全部在image內部時,開始卷積.?
- same還有另外一個意思;
- 卷積后輸出的feature?map尺寸保持不變(相對于輸入圖片);
- same模式不代表完全輸入輸出尺寸一樣;
- 同卷積核的步長有關系;
- same模式是最常見的模式;
- 該模式可以在卷積過程中保持圖像大小不變;?
三通道卷積
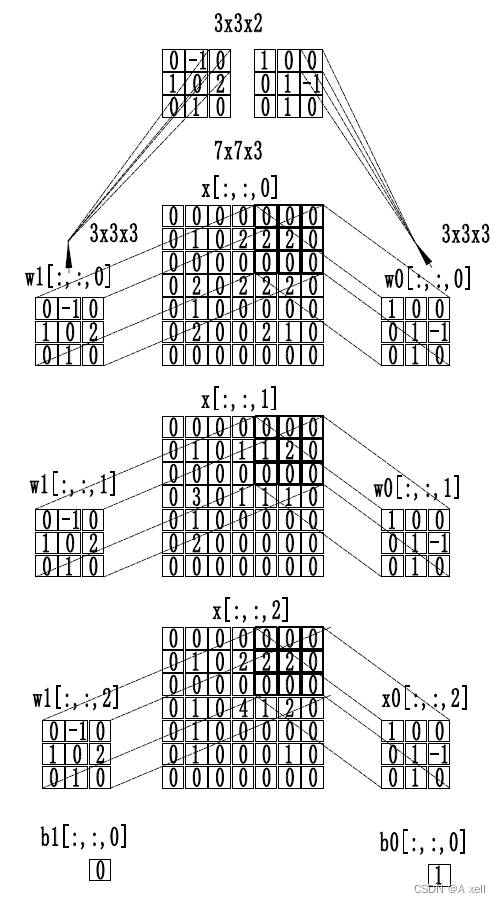
卷積核的確定
- CNN的厲害在于:
- 過濾器的特征不是人為設定;
- 而是通過大量圖片自己訓練出來的;
?
(八))

——排序算法)



按鍵產生中斷)


、查看equals底層、final--學習JavaEE的day15)
)

部署CNI網絡插件(4))



算法)
)

