1. 題目

給定一個包含非負整數的數組?nums?，返回其中可以組成三角形三條邊的三元組個數。

2. 示例

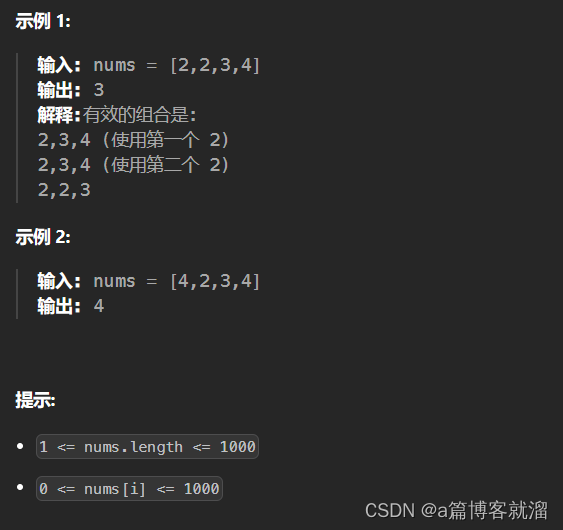
3. 分析?

利用已升序了的數組通過 a + b > c 這條公式找出符合要求的三元組，利用這個公式的前提是三條邊為從小到大，再利用單調性快速統計出符合要求的三元組個數。

解題方法：

1. 先固定到最大的數(c)，即nums[nums.size()-1]。
2. 再最大數的左區間內，定位一左(a)一右(b)指針分別指向區間左右。

現在就可以開始尋找符合要求的三條邊了。
兩邊之和有兩種情況：

• a + b > c
  這是符合要求的情況。我們知道數組是升序的，因為此時 left(a) + right(b) 已經是大于 c 了，那么[left+1, right-1] (a)這個區間內的數 + right(b) 也是肯定大于 c 了，因為數組是升序的(單調性)。所以此時符合要求的三元組個數就為(right-left)，這個組合下的right(b)可以舍棄掉了，再--看下一個b的情況即可。
• a + b <= c
  這是不符合要求的情況，為無效三角形。因為此時 left(a) + right(b) 已經是小于或等于 c 了，那么[left+1, right-1] (a)這個區間內的數 + right(b) 也是肯定小于或等于 c 了，因為數組是升序的(單調性)。這個組合下的left(a)可以舍棄掉了，再++看下一個a的情況即可。

當區間內的所以情況判斷完畢，即最大數的所有組合已統計完畢，再重新固定新的最大數，即上一個最大數的前一位數，再去統計符合要求的三元組個數。

---

class Solution {
public:int triangleNumber(vector<int>& nums) {// 1. 升序sort(nums.begin(), nums.end());// 2. 雙指針int ret = 0, n = nums.size();for(int i = n-1; i >= 2; i--)// 固定最大的數，因為是三元組，從2開始{// 利用雙指針統計出符合要求的三元組的個數int left = 0, right = i - 1;while (left < right){if (nums[left]+nums[right] > nums[i]){ret += right - left;right--;}else{left++;}}}return ret;}
};