
?💯 博客內容:【茶話數據結構】查找最短路徑——Dijkstra算法詳解
😀 作??者:陳大大陳
🦉所屬專欄:數據結構筆記
🚀 個人簡介:一個正在努力學技術的準前端,專注基礎和實戰分享 ,歡迎私信!
💖 歡迎大家:這里是CSDN,我總結知識和寫筆記的地方,喜歡的話請三連,有問題請私信 😘 😘 😘
目錄
題記?
兩大注意事項
實例題目
超超超詳細圖解
?答案以及詳盡總結
后記
題記?
?復習到離散數學圖論時,想起來這個算法,感覺很有寫博客的必要!今天這篇博客就來講一下查找最短路徑的Dijkstra算法。
Dijkstra 算法,是由荷蘭計算機科學家 Edsger Wybe Dijkstra 在1956年發現的算法,戴克斯特拉算法使用類似廣度優先搜索的方法解決賦權圖的單源最短路徑問題。Dijkstra 算法原始版本僅適用于找到兩個頂點之間的最短路徑,后來更常見的變體固定了一個頂點作為源結點然后找到該頂點到圖中所有其它結點的最短路徑,產生一個最短路徑樹。本算法每次取出未訪問結點中距離最小的,用該結點更新其他結點的距離。需要注意的是絕大多數的Dijkstra 算法不能有效處理帶有負權邊的圖。
兩大注意事項
需要注意兩個問題
1.每次從未標記的節點中選擇距離出發點最近的節點,標記它,收錄到最短路徑集合中。
2.計算剛加入的節點A的臨近節點B的距離(不包含標記的節點),若(節點A的距離+節點B的距離到節點B的邊長)<節點B,就更新節點B的距離和其前一個位置的點。
實例題目
?如圖,計算從起點0到終點4的最短路徑長度。?

超超超詳細圖解
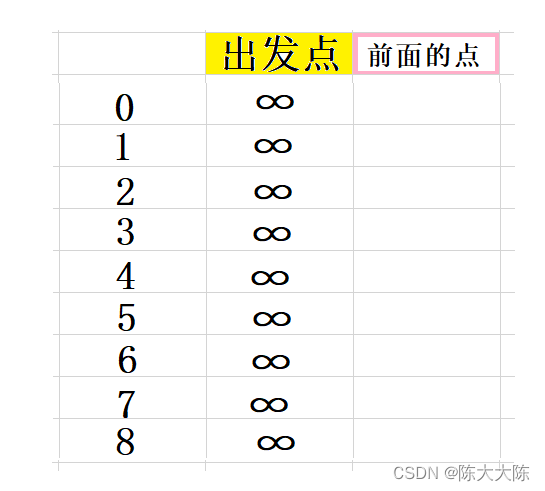
?我們作出這樣的表格,用于施展Dijkstra算法。
出發點表示從出發點到現在位置地距離。
首先從距離出發點最近的點,也就是出發點開始,它距離出發點的位置顯然是0,。
標記它,并收錄到最優路徑集合中,我們用一個對鉤來表示已被收錄。

?下一步就是找它的臨近節點,分別是1和7。
更新1和7的出發點距離和前面點,如圖。

?緊接著從沒有被標記的節點中選出出發點距離最短的,即為1,標記它,并收錄到最短路徑集合中。
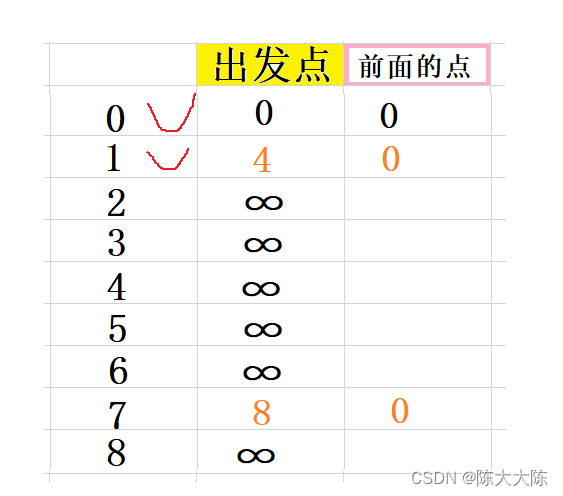
緊接著計算它的鄰接節點,即為7和2,因為0已經被標記所以不算。
計算出0和它們的距離分別是15和12,12小于默認的正無窮,更新。
15比8大,不更新。

?選出出發點距離最小的點,即為7,標記它,并收錄到最短路徑集合中。
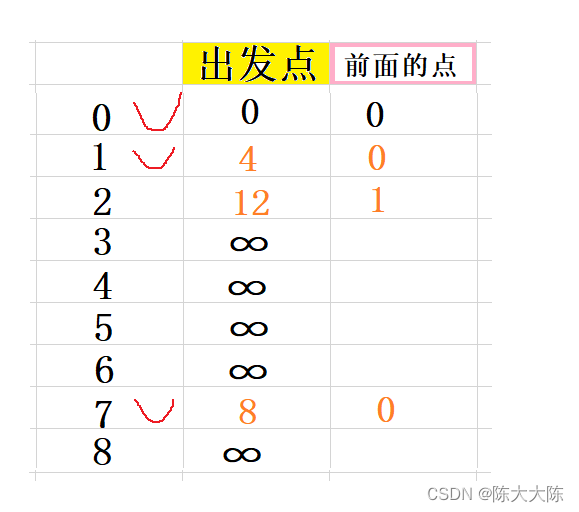
緊接著計算它的鄰接節點,即為6和8,因為1和0已經被標記所以不算。
計算出0和它們的距離分別是9和15,小于默認的正無窮,更新。

?選出出發點距離最小的點,即為6,標記它,并收錄到最短路徑集合中。
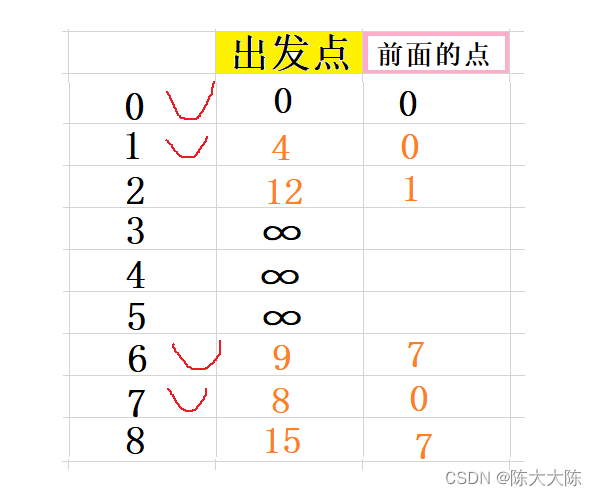
緊接著計算它的鄰接節點,即為5和8,因為7已經被標記所以不算。
計算出0和它們的距離分別是11和15,11的更新,15的和之前相等,不更新。

??選出出發點距離最小的點,即為5,標記它,并收錄到最短路徑集合中。

緊接著計算它的鄰接節點,即為2,3和4,因為6已經被標記所以不算。
計算出0和它們的距離分別是15和25和21。
15大于12,不更新,25小于正無窮,更新,21小于正無窮,更新。
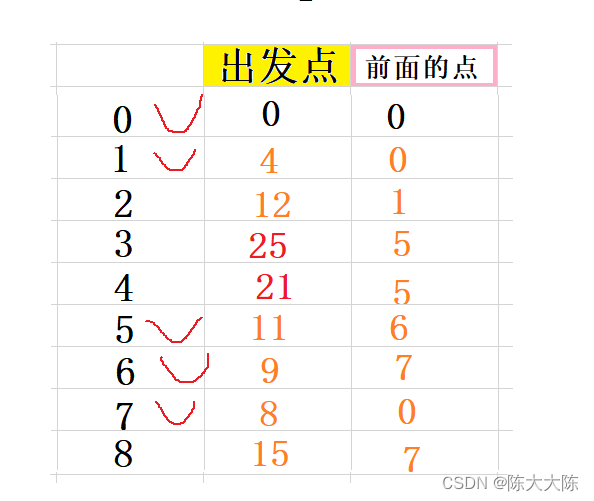
?選出出發點距離最小的點,即為2,標記它,并收錄到最短路徑集合中。

緊接著計算它的鄰接節點,即為3和8,因為1和5已經被標記所以不算。
計算出0和它們的距離分別是19和14,分別小于25和15,都更新。
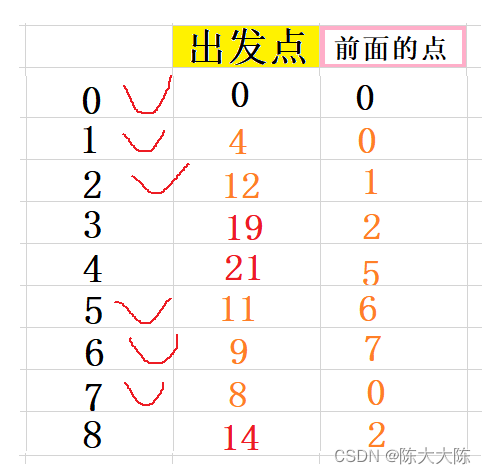
?選出出發點距離最小的點,即為8,標記它,并收錄到最短路徑集合中。

緊接著計算它的鄰接節點,全都標記過了,最方便的一集,小時候寫哭了。
直接標記后跳過。
?選出出發點距離最小的點,即為8,標記它,并收錄到最短路徑集合中。

緊接著計算它的鄰接節點,就剩下一個4沒被標記了。
計算出距離它的距離是28,大于21,不更新。
最后一步將4標記,并收錄到最短路徑集合中。、
我們的最終答案堂堂出爐!!!

?答案以及詳盡總結
從上面的表中可以得到答案,0到4的最短路徑是21。
從頭到尾經過的節點是 0 7 6 5 4。
其實需要注意的就這兩點。?
1.每次從未標記的節點中選擇距離出發點最近的節點,標記它,收錄到最短路徑集合中。
2.計算剛加入的節點A的臨近節點B的距離(不包含標記的節點),若(節點A的距離+節點B的距離到節點B的邊長)<節點B,就更新節點B的距離和其前一個位置的點。
后記
韓信帶凈化,成為大牛道阻且長,小僧還在山腰上。。。
博客里如果有問題的話,還請大佬私信我,我會修改的。
有問題的話請私信問我,我看到就會回的。?








)










