一、效果圖
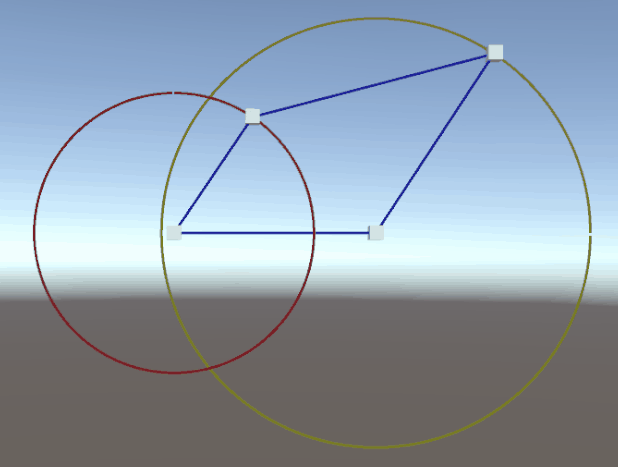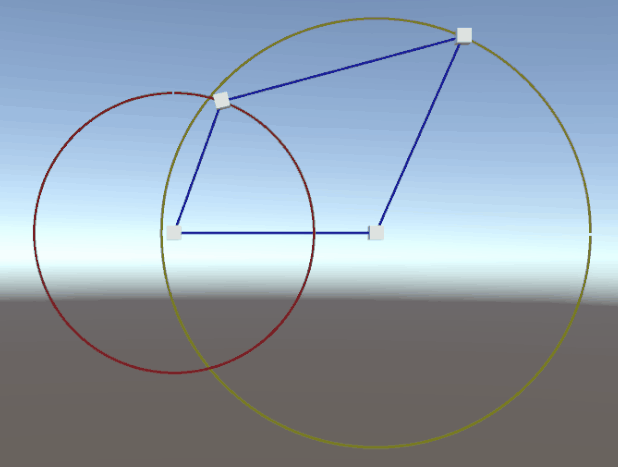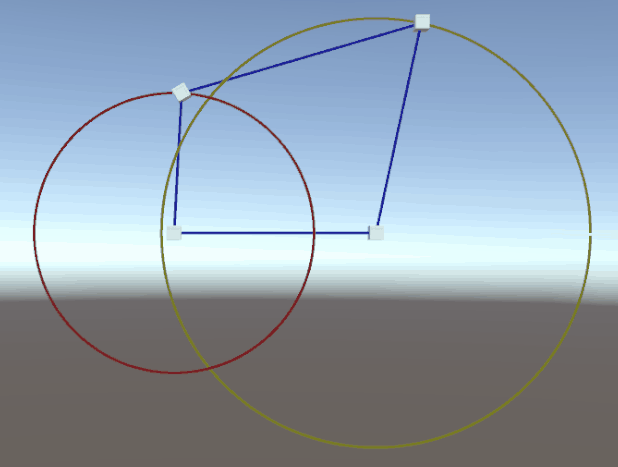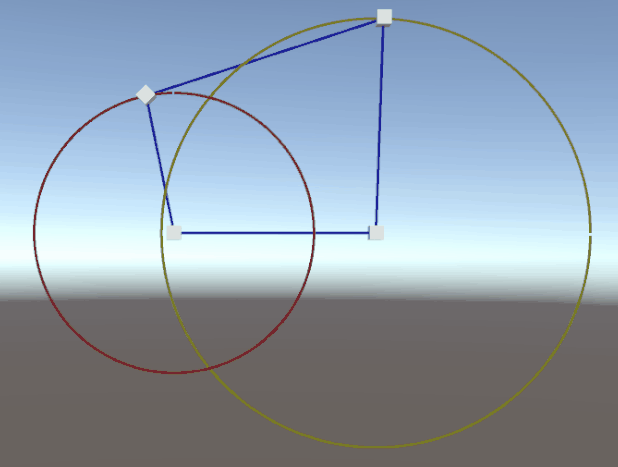
設定好各邊長度和轉速后,點擊【設置并啟動】,自動生成一個機構模型,并按照原理進行運轉
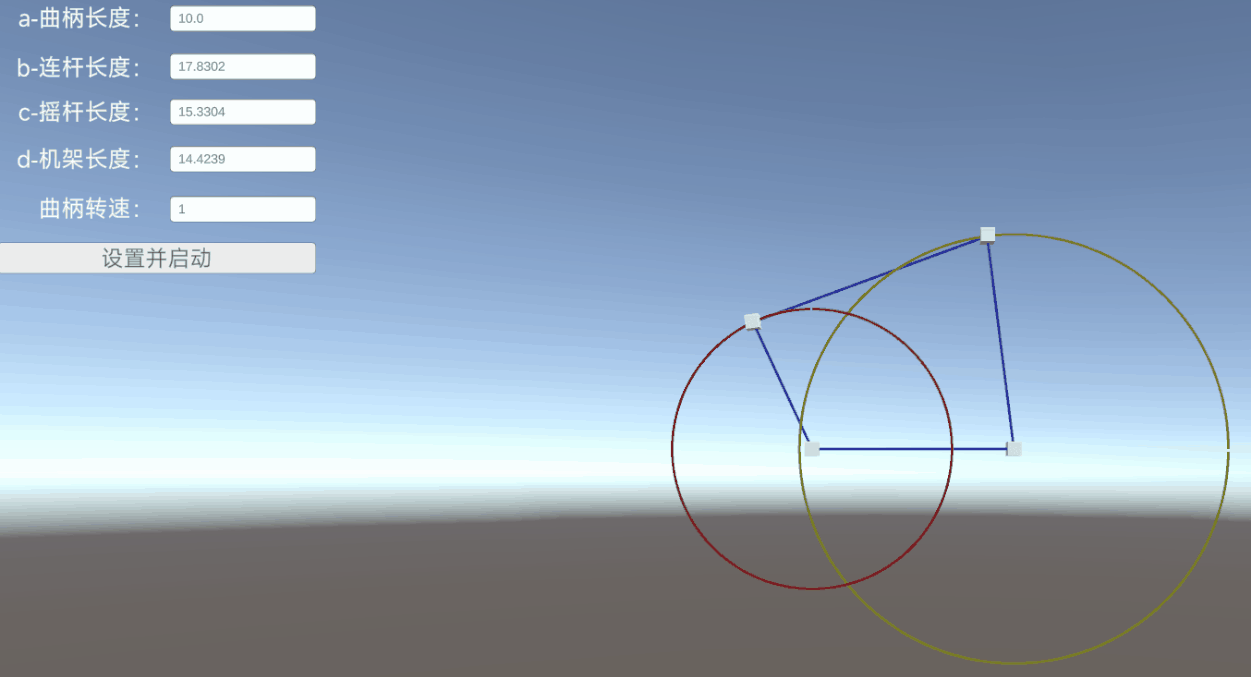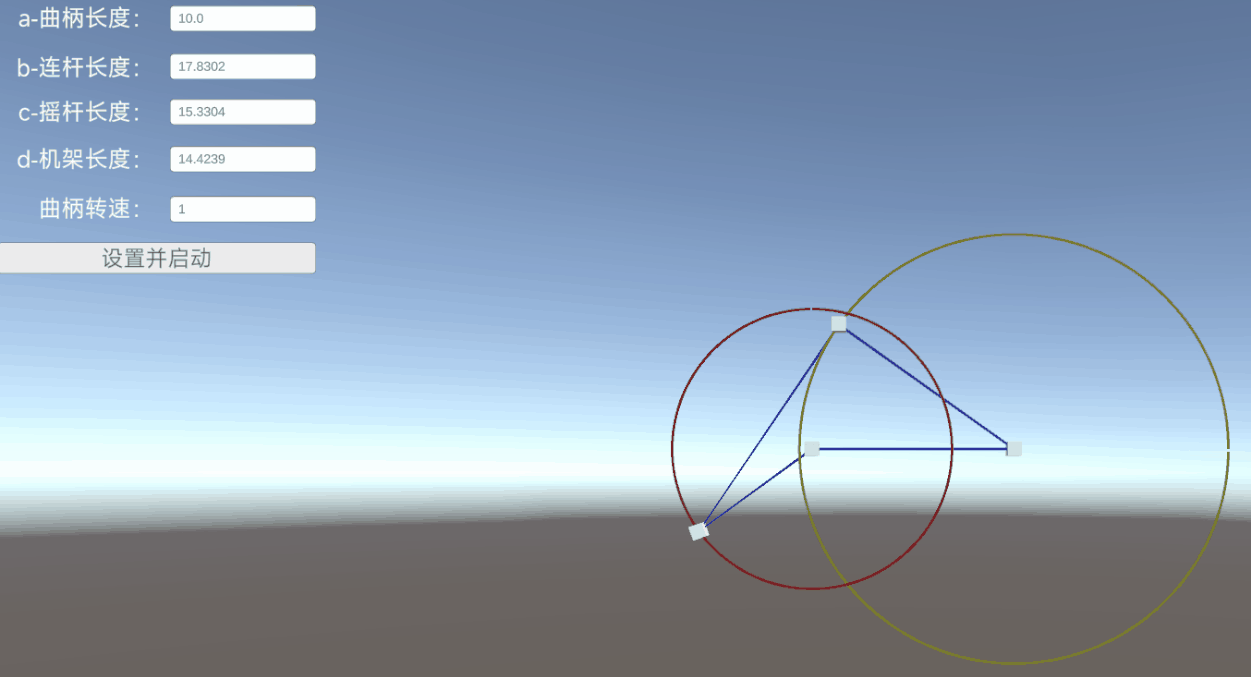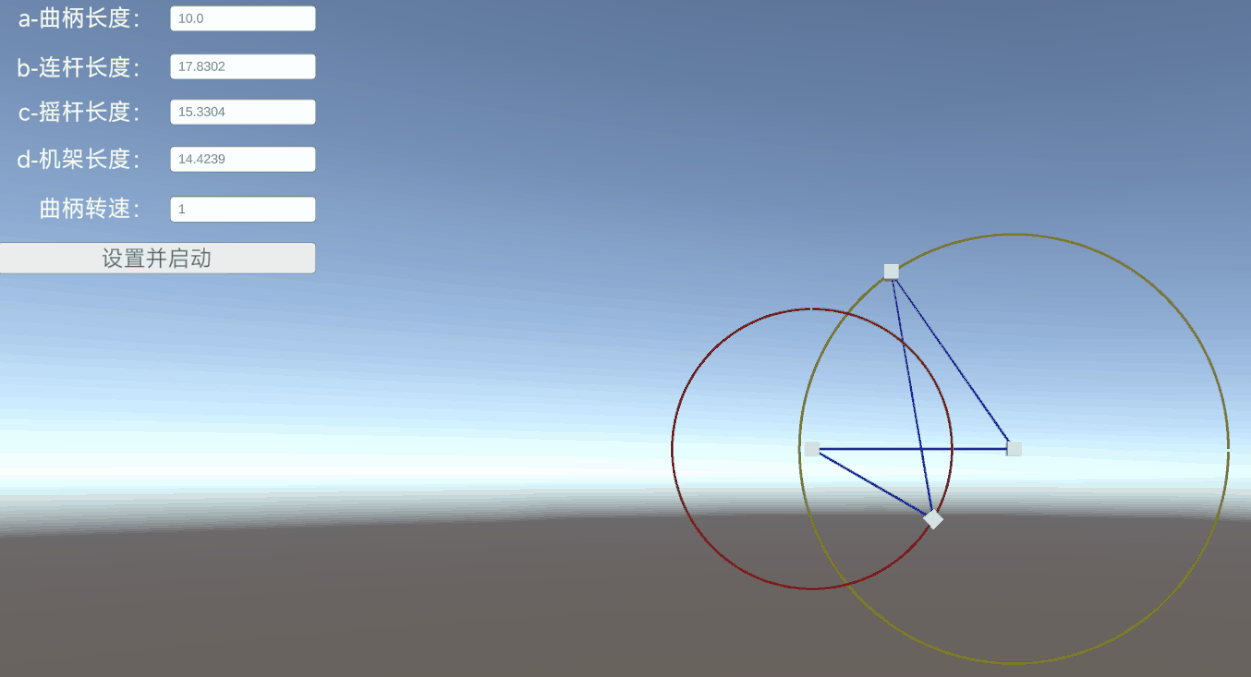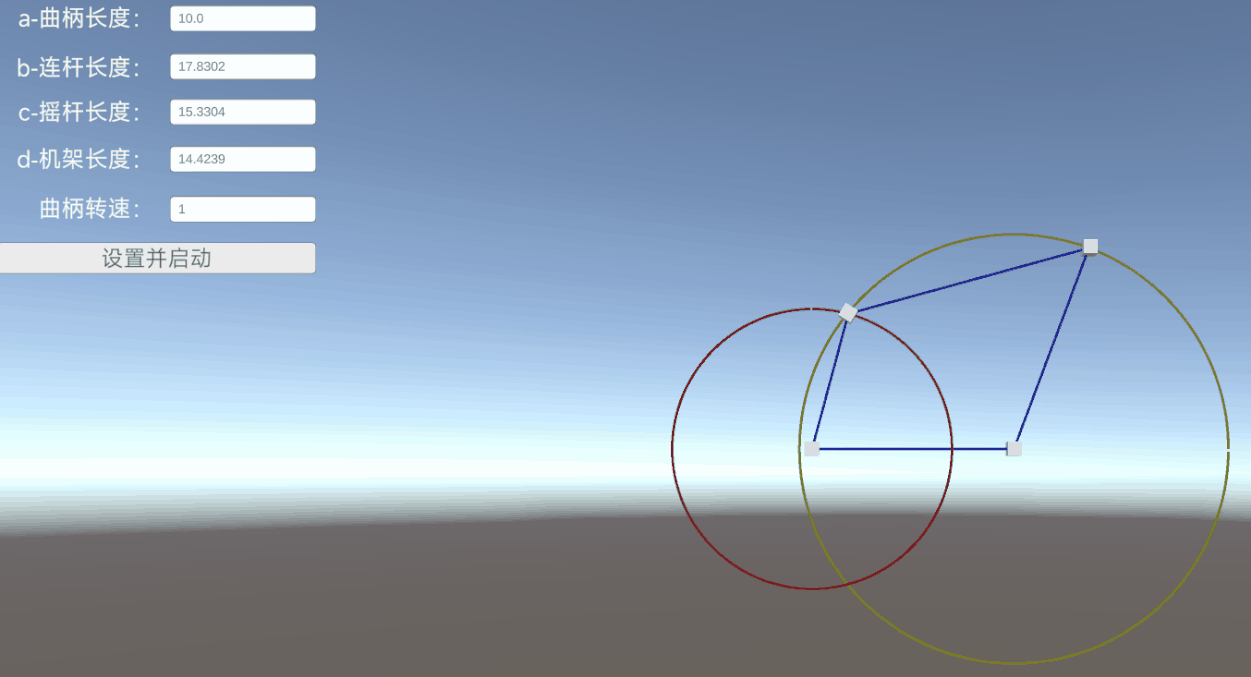
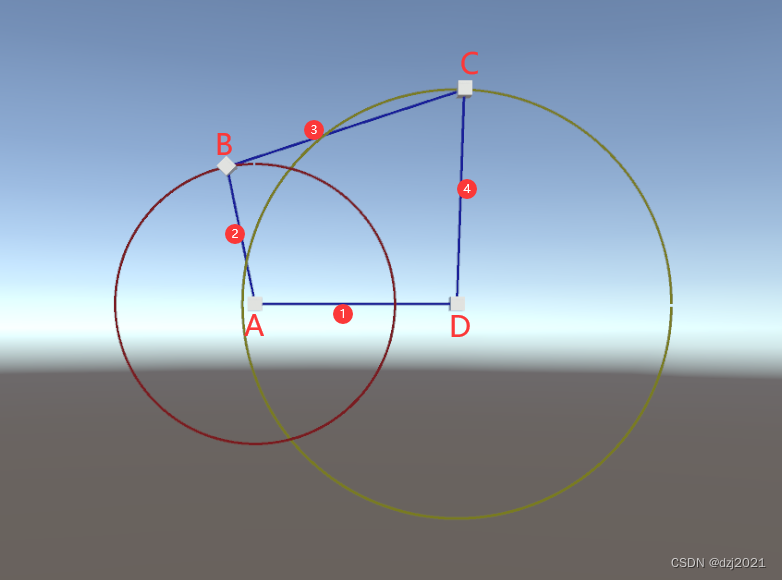
二、鉸鏈四桿機構介紹
機架:A和D是固定位置,叫做機架。
曲柄:B點繞A點旋轉,構成曲柄。
連桿:C點和B點相連,構成連桿。
搖桿:C點繞著D點轉動,構成搖桿。
三、運動原理
1、機構示意圖
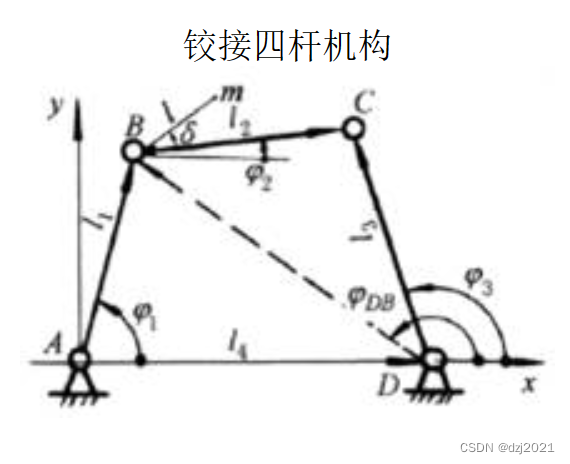
第一步:計算Φ1(∠BAD)
曲柄轉動了多少度
第二步:計算BD的長度
已知B點和D點位置,計算BD的長度,可用機械公式計算,或者直接使用Vector3.Distance計算。
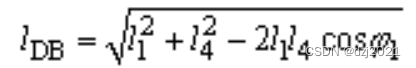
第三步:計算∠ΦDB(∠BDA’)
-
(1)用機械原理公式計算的依據:
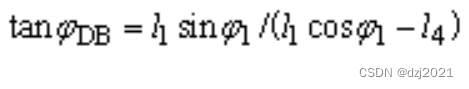
-
(2)直接用Unity向量距離api計算:
Vector3.Distance(A, D);//示例代碼
第四步:計算計算∠Φ3的值
只能用機械原理的公式計算:
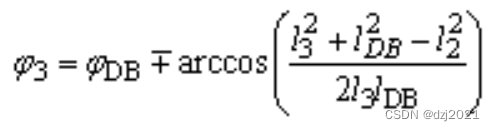
第五步:根據∠Φ3計算C點位置
∠Φ3已知的時候,在射線DC上取C點
四、關鍵代碼實現
代碼為計算部分的代碼,僅供交流學習之用。
/// <summary>/// 計算曲柄和搖桿位置/// </summary>/// <returns></returns>bool JiSuanWeiZhi(){//設定B的位置 AB = avar posB = A.transform.position + (B.transform.position - A.transform.position).normalized * (float)a_AB;B.transform.position = posB;//計算Φ1(∠BAD)double phi1 = Vector3.Angle(B.transform.position - A.transform.position, D.transform.position - A.transform.position);//象限判斷if (B.transform.position.y < A.transform.position.y){phi1 = 360 - phi1;}//公式計算lenDB的值var lDB2 = math.sqrt(a_AB * a_AB + d_DA * d_DA - 2 * a_AB * d_DA * Cos(phi1.ToRadians()));//計算ΦDB(∠BDA')double phiDB = Vector3.Angle(B.transform.position - D.transform.position, D.transform.position - A.transform.position);//象限處理if (B.transform.position.y < A.transform.position.y){phiDB = 360 - phiDB;}//計算Φ3的值var phi3 = phiDB - Acos((c_CD*c_CD + lDB2 * lDB2 - b_BC * b_BC)/(2 * c_CD * lDB2)).ToDegrees();//擺放C點if (double.IsNaN(phi3)){Debug.Log($"無法計算Φ3的值 {(c_CD*c_CD + lDB2 * lDB2 - b_BC * b_BC)/(2 * c_CD * lDB2)}");return false;}else{Quaternion q = Quaternion.AngleAxis((float)phi3, new Vector3(0,0,1));var dir = q * (D.transform.position - A.transform.position);C.transform.position = D.transform.position + dir.normalized * (float)c_CD;}return (true);}
五、機械原理附錄:
1、平面示意圖
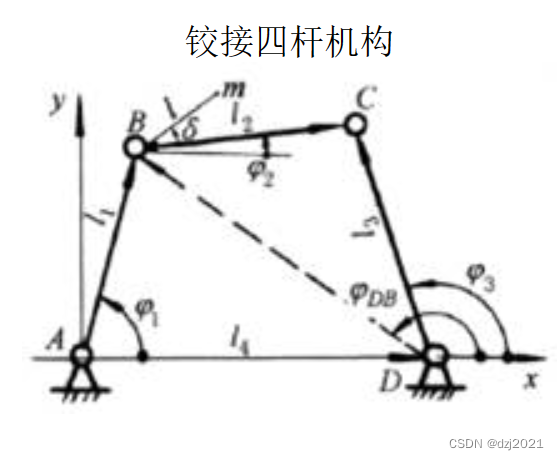
2、運動分析公式——位置計算
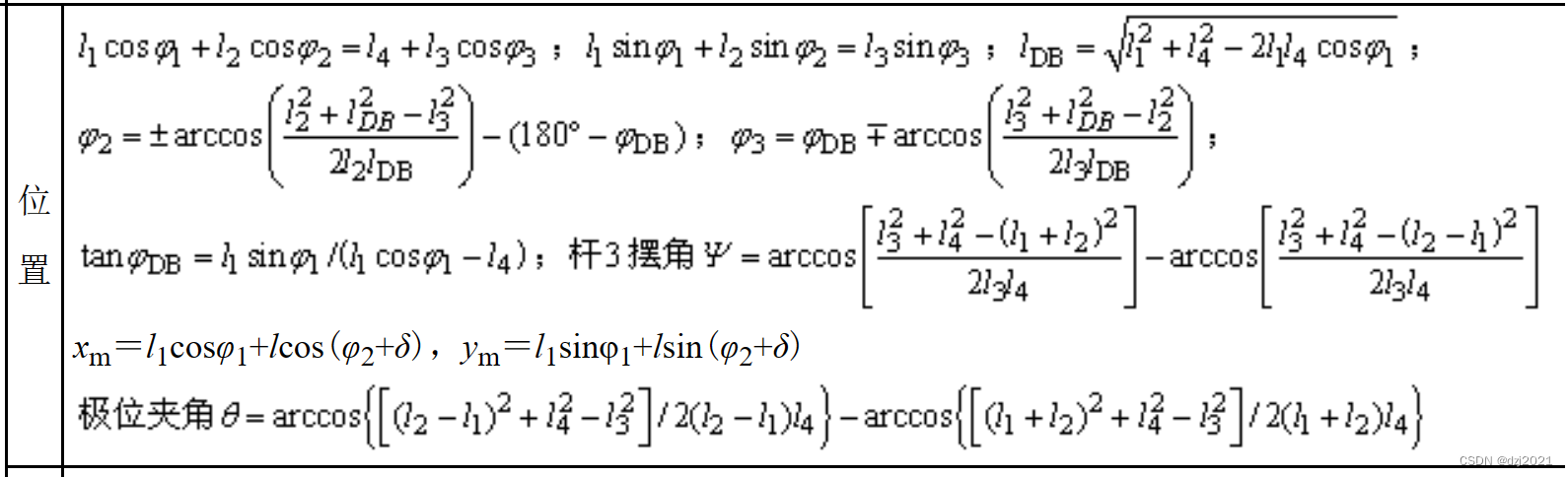
3、運動分析公式——速度計算
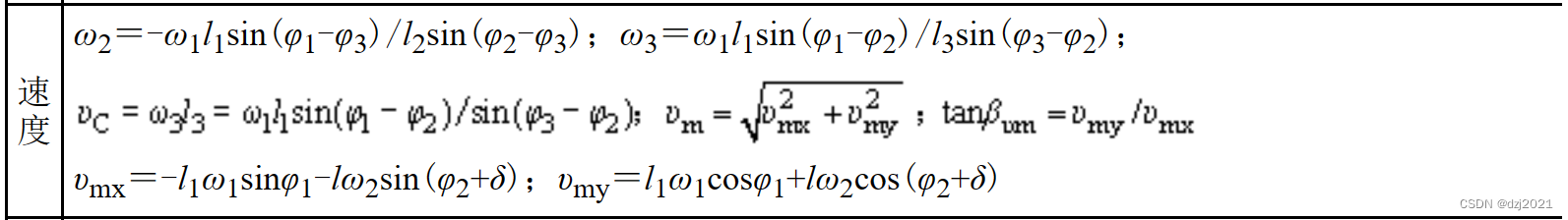
4、運動分析公式——加速度計算
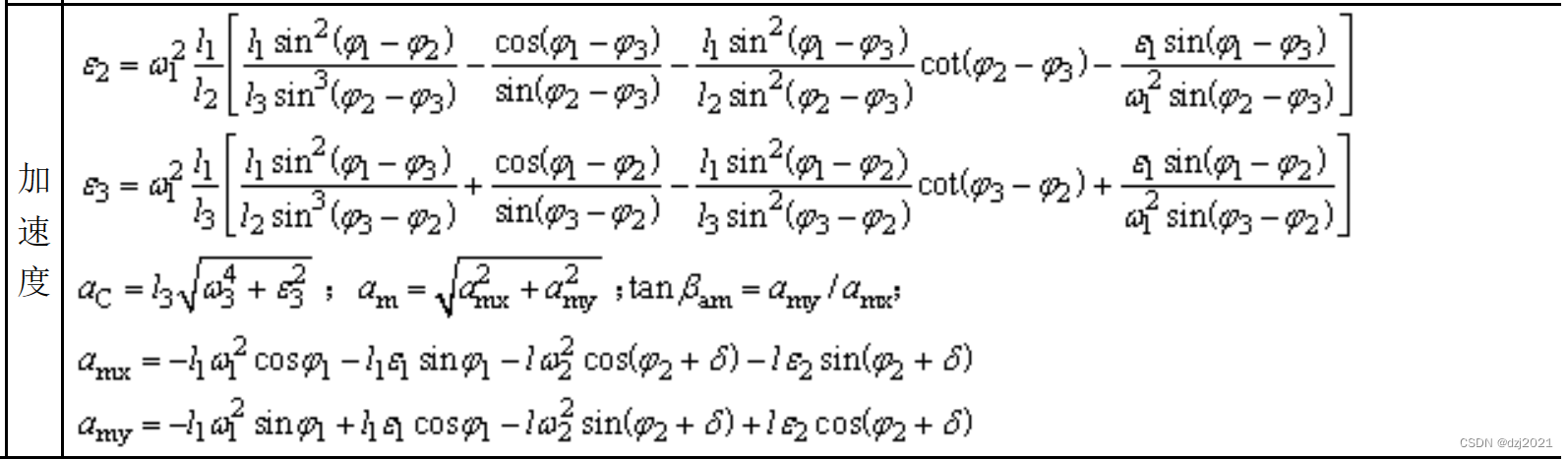




(下))

求解23個基準函數)



:Sora技術路徑整體認知)


)





