? ? ? ?

目錄

1、紅黑樹的規則

2、紅黑樹節點的定義?

3、紅黑樹插入節點的調整操作

3.1 情況一

3.2 情況二

3.3 情況三?

4、紅黑樹的實現

結語

---

前言：

????????在C++中，紅黑樹是二叉搜索樹的另一種優化版本，他與AVL樹的區別在于保持樹的平衡方式不同，AVL樹保持平衡的方式是在節點中多存儲一個成員來記錄平衡因子，紅黑樹保持平衡的方式也是增加了一個成員，但是該成員的作用是記錄節點的兩種狀態（顏色）：紅色--黑色。當然只記錄顏色并不能保持平衡，紅黑樹還規定最長路徑的節點個數不會超過最短路徑的節點個數的兩倍，因此紅黑樹不會因為插入有序數據而演變成“單支樹”。

1、紅黑樹的規則

? ? ? ? 紅黑樹有如下規則：

? ? ? ? 1、顧名思義，紅黑樹的節點只能有黑色和紅色兩種狀態。

? ? ? ? 2、根結點默認為黑色。

? ? ? ? 3、紅色節點的兩個孩子只能是黑色節點。

? ? ? ? 4、插入的節點默認為紅色節點。

? ? ? ? 5、每條路徑的黑色節點都相同。

? ? ? ? 紅黑樹正確示意圖：

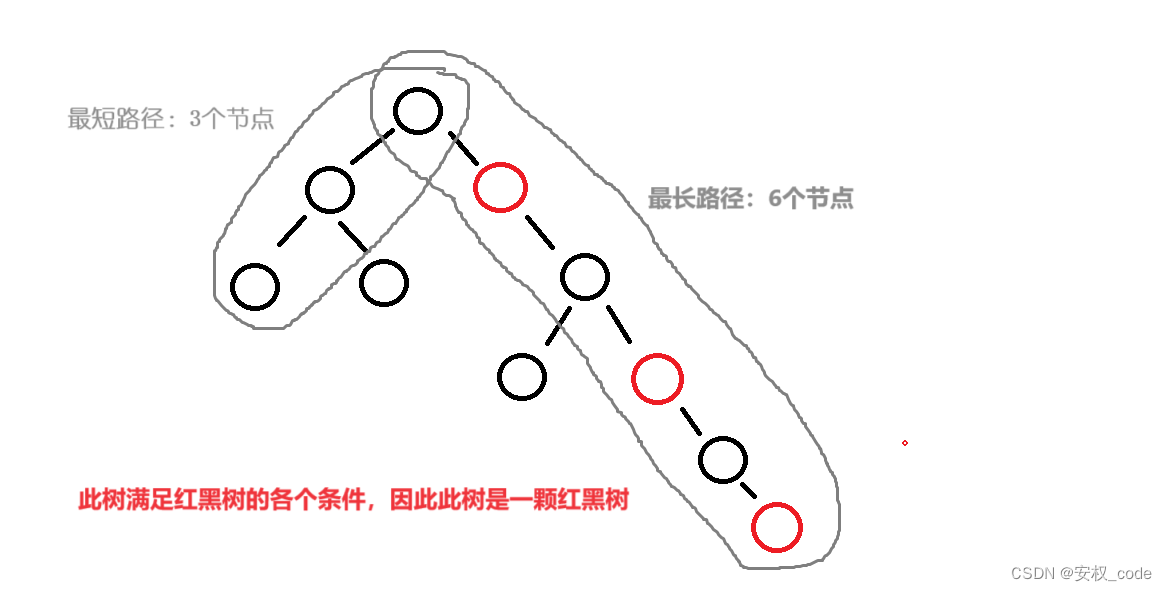
? ? ? ? ?紅黑樹錯誤示意圖：

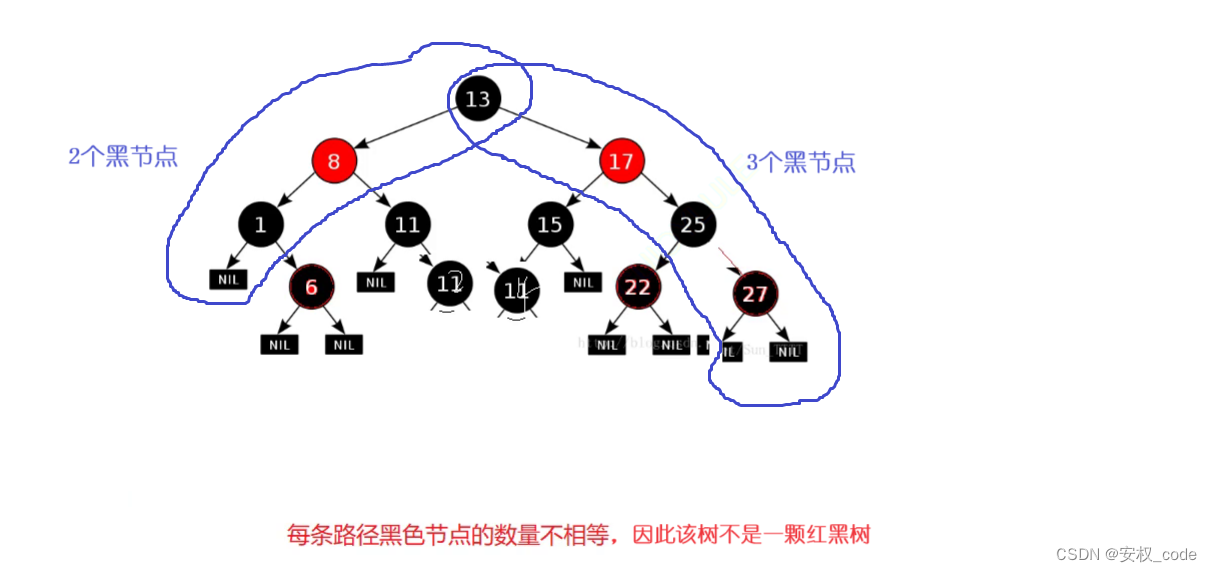
2、紅黑樹節點的定義?

? ? ? ? 通過上述對紅黑樹的簡述，可以給出紅黑樹的節點代碼：

#define _CRT_SECURE_NO_WARNINGS 1enum Colour//定義一個枚舉
{RED,BLACK,
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;//指向左孩子RBTreeNode<K, V>* _right;//指向右孩子RBTreeNode<K, V>* _parent;//指向父母節點pair<K, V> _kv;//記錄數據Colour _col;//若是AVL樹這里記載的是平衡因子，紅黑樹是顏色RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED)//默認插入的節點是紅色{}
};

? ? ? ? 可以發現，紅黑樹的節點代碼幾乎和AVL樹一模一樣，只是控制平衡的條件有區別，僅此而已。?

3、紅黑樹插入節點的調整操作

? ? ? ? 紅黑樹的插入函數可以分兩個步驟：

? ? ? ? 1、找到合適的位置插入，即二叉搜索樹插入的邏輯（小于根節點的放在左邊，大于根節點的放在右邊）。

? ? ? ? 2、因為插入的節點默認為紅色，則插入節點后，查看當前樹是否破壞了紅黑樹的規則，即觀察其節點的父母節點是否為紅色，如果是則需要進行調整操作（規則3）。

? ? ? ? 在分析之前，先確定好節點之間的關系名稱（cur表示新插入的節點，parant表示父母節點，uncle表示叔叔節點，gparent表示祖父節點）：

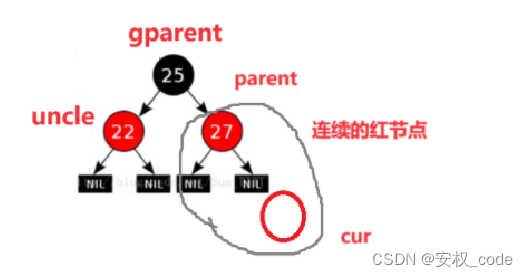
3.1 情況一

????????當叔叔節點存在且為紅，父母節點為紅，祖父節點為黑：

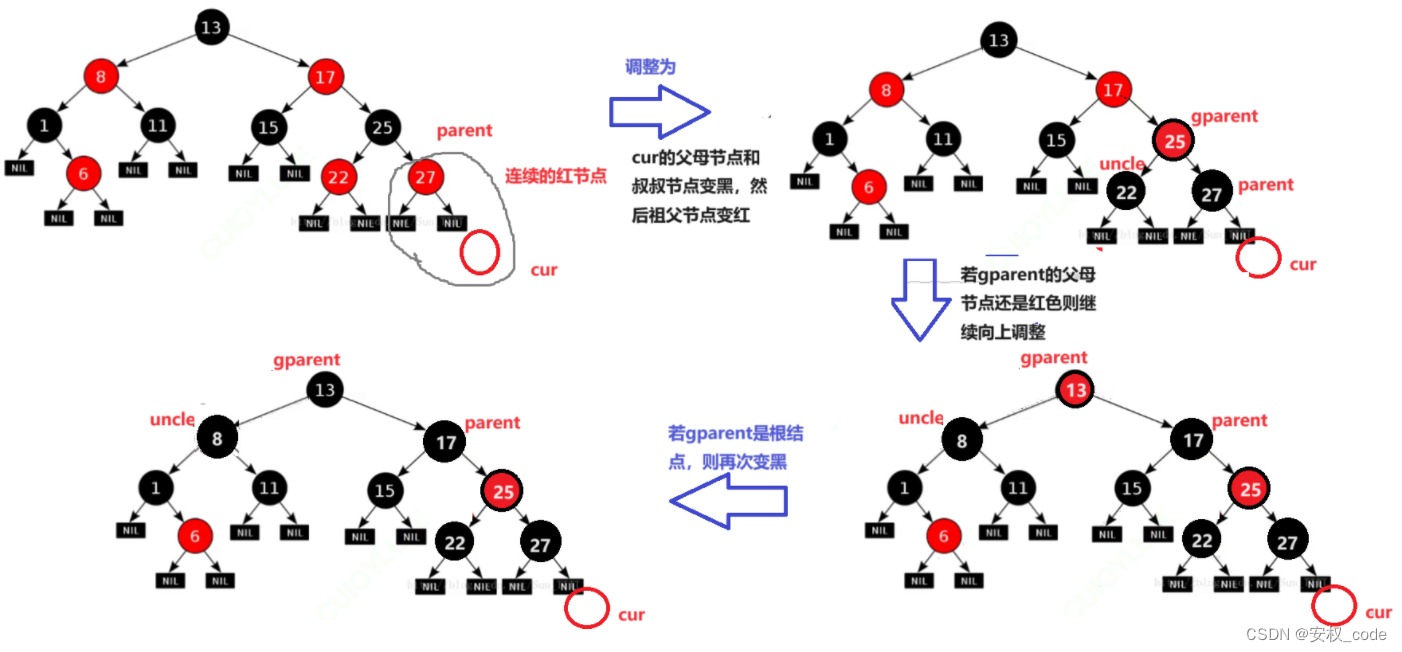
? ? ? ? 最后可以發現，經過一系列的調整后符號紅黑樹的規則。

3.2 情況二

? ? ? ? 情況二又分兩種情況：1、叔叔節點為黑色。2、不存在叔叔節點。

? ? ? ? 1、其他條件和情況一相同，但是叔叔節點是黑色的：

? ? ? ? 從上圖可以發現，情況二多了旋轉的步驟，并且在旋轉之后將parent變黑，gparent變紅，最終結果滿足紅黑樹的規則。

? ? ? ? 2、若不存在叔叔節點：

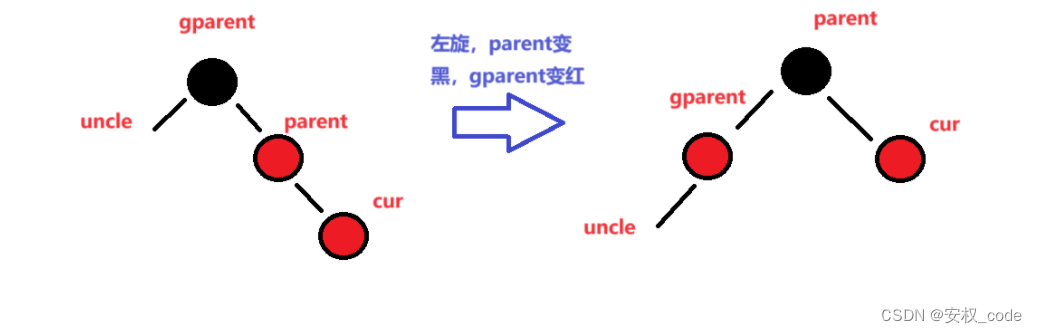
? ? ? ? 綜上所述，情況二可以總結為：旋轉+變色（parent變黑，gparent變紅）。?

3.3 情況三?

? ? ? ? 情況三即以上情況的插入點不一樣，以上情況的插入節點都是插入在“邊緣處”，通俗來講就是左子樹插入的節點都是作為左孩子插入的，而右子樹插入的節點都是作為右孩子插入的，但是實際中總會出現在右子樹中插入的節點是以左孩子的形式插入的（如下圖），拿上述情況二的第二種情況舉例，若插入的cur在parent的左邊，那么以上的處理方法顯然不能解決問題，具體操作圖如下：

4、紅黑樹的實現

? ? ? ? 紅黑樹的實現代碼如下：

#define _CRT_SECURE_NO_WARNINGS 1#include<iostream>
using namespace std;enum Colour//定義一個枚舉
{RED,BLACK,
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;//指向左孩子RBTreeNode<K, V>* _right;//指向右孩子RBTreeNode<K, V>* _parent;//指向父母節點pair<K, V> _kv;//記錄數據Colour _col;//若是AVL樹這里記載的是平衡因子，紅黑樹是顏色RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED)//默認插入的節點是紅色{}
};template<class K, class V>
class RBTree//紅黑樹類
{typedef RBTreeNode<K, V> Node;
public:~RBTree(){_Destroy(_root);_root = nullptr;}
public:bool Insert(const pair<K, V>& kv)//插入函數{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//第一次插入的根結點手動置黑return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//當parent為紅色則違法規則，需要調整while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (grandfather->_left == parent)//父母在祖父的左邊{Node* uncle = grandfather->_right;// 情況1：叔叔節點存在且為紅，叔叔和父母進行變色處理，并繼續往上處理if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 繼續往上調整cur = grandfather;parent = cur->_parent;}else // 情況2：叔叔不存在/叔叔存在且為黑，旋轉+變色{//父母在祖父的左邊，而cur在父母的左邊，說明是“邊緣”情況if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//對應所述的情況三，需要旋轉兩次，并且cur變成了根結點{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else // 父母在祖父的右邊{Node* uncle = grandfather->_left;// 情況1：u存在且為紅，變色處理，并繼續往上處理if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 繼續往上調整cur = grandfather;parent = cur->_parent;}else // 情況2：叔叔不存在/叔叔存在且為黑，旋轉+變色{//以下邏輯同上思路，只不過邏輯相反if (cur == parent->_right){RotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;//根結點始終為黑return true;}void InOrder(){_InOrder(_root);}bool IsRedB()//檢查紅黑樹{if (_root && _root->_col == RED){cout << "根節點顏色是紅色" << endl;return false;}int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)++benchmark;cur = cur->_left;}// 連續紅色節點return _Check(_root, 0, benchmark);}int Height(){return _Height(_root);}private:void _Destroy(Node* root)//釋放空間{if (root == nullptr){return;}_Destroy(root->_left);_Destroy(root->_right);delete root;}int _Height(Node* root){if (root == NULL)return 0;int leftH = _Height(root->_left);int rightH = _Height(root->_right);return leftH > rightH ? leftH + 1 : rightH + 1;}bool _Check(Node* root, int blackNum, int benchmark)//紅黑樹的驗證{if (root == nullptr)//走到空，就判斷黑色節點數量是否一樣{if (benchmark != blackNum){cout << "某條路徑黑色節點的數量不相等" << endl;return false;}return true;}if (root->_col == BLACK)//重新記錄每條路徑下的黑色節點{++blackNum;}if (root->_col == RED&& root->_parent&& root->_parent->_col == RED)//連續紅色節點也會報錯{cout << "存在連續的紅色節點" << endl;return false;}//每次遞歸都把黑色節點數量傳給下一個棧幀return _Check(root->_left, blackNum, benchmark)&& _Check(root->_right, blackNum, benchmark);}void _InOrder(Node* root)//中序遍歷打印{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}void RotateL(Node* parent)//左旋{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppnode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppnode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}}void RotateR(Node* parent)//右旋{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppnode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}}private:Node* _root = nullptr;
};int main()
{int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };RBTree<int, int> t1;for (auto e : a){t1.Insert(make_pair(e, e));}t1.InOrder();//j檢查打印出來的數據是否有序cout << endl << t1.IsRedB() << endl;return 0;
}

? ? ? ? ?運行結果：

? ? ? ? 從上面代碼可以看出，檢驗一棵樹是否為紅黑樹，從以下幾個方面進行判斷：函數IsRedB的作用是判斷根結點是否為黑色，然后隨便遍歷一條路徑，記錄該路徑下黑色節點的數量（規則5）。?

? ? ? ? 接著把記錄下來的黑色節點數量傳給函數_check，并且讓_check函數把所有路徑下的黑色節點記錄下來，一一的去跟之前記錄好的數據進行對比，若有不相等的情況說明該樹不是紅黑樹，另外_check函數內還進行了紅色節點是否連續的判斷（規則3）。

結語

? ? ? ? 以上就是關于紅黑樹的講解，紅黑樹的重點還是在于了解紅黑樹的調整邏輯，理清叔叔節點和父母節點他們的位置關系，最核心的還是叔叔節點，他的存在與否，是紅色還是黑色都影響最終的調整規律。最后希望本文可以給你帶來更多的收獲，如果本文對你起到了幫助，希望可以動動小指頭幫忙點贊👍+關注😎+收藏👌！如果有遺漏或者有誤的地方歡迎大家在評論區補充，謝謝大家！！