搭建之前的基礎與思考
構建模型的基本思想:
構建深度學習的過程:產生idea,將idea轉化成code,最后進行experiment,之后根據結果修改idea,繼續idea–>code–>experiment的循環,直到最終訓練到表現不錯的深度學習網絡模型。
BP網絡的搭建
BPNN v-0.1
目標:搭建一個有學習能力的BP神經網絡。
目標完成情況:
●局限:只能計算固定大小的數據尺寸
●局限:只有一層,即為感知機或單層神經網絡
有一定了解的可以直接看到代碼,代碼注釋有思路。
idea
●神經元(單層感知機):接收n維列向量x(特征維度為n),輸出y的估計。
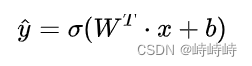
多組輸入x,可以按列堆疊形成矩陣。
●激活函數:Sigmoid、ReLU等
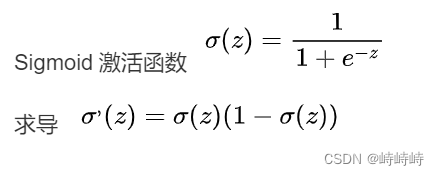
●損失函數:量化模型預測值與真實值的偏差,模型訓練的目的是讓Loss盡可能小。
例如: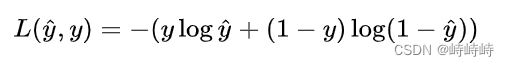
成本函數就是所有訓練樣本損失函數的平均。
●反向傳播時的復合求導
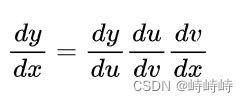
反向傳播時只需要計算每一層的導數,最后乘積即可。
整體復盤以及數據流向圖
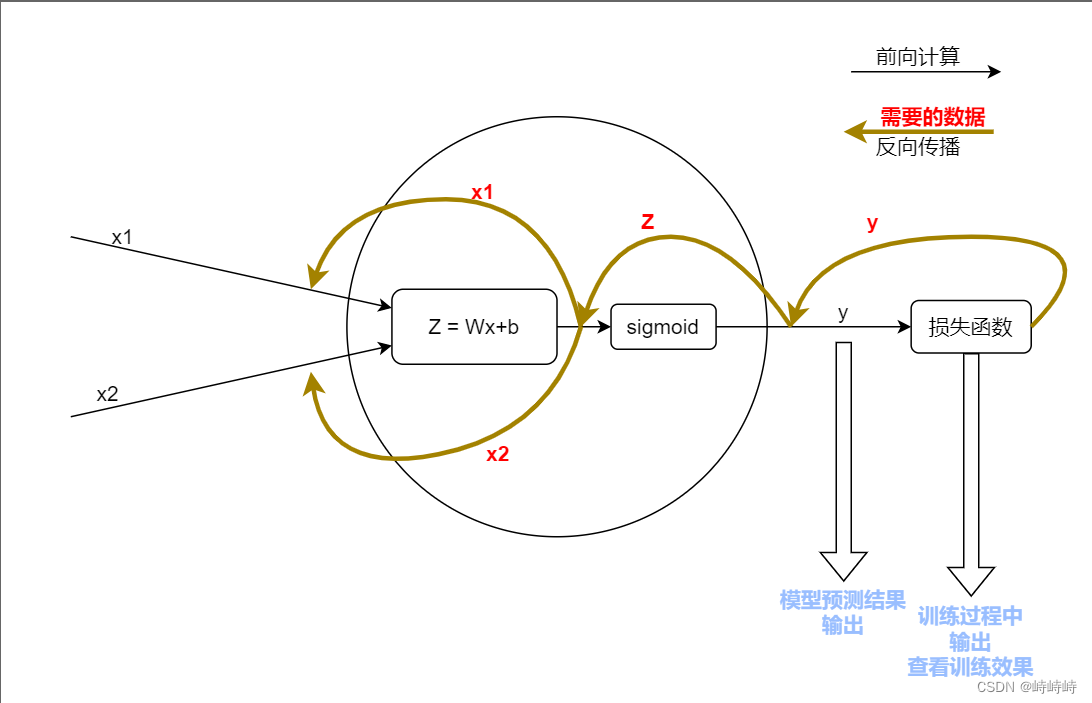
code
根據面向對象編程思想,有兩種實現思路,以神經元為最小類或以神經網絡為最小類。
這里為了有更清晰的層次選擇以神經元為最小類。
自己早數據,假設數據是學生的身高體重,根據此二者預測學生性別。
# Define dataset,已經經過預處理,保留特征
data = np.array([[-2, -1], # Alice[25, 6], # Bob[17, 4], # Charlie[-15, -6], # Diana
])
all_y_trues = np.array([1, # Alice0, # Bob0, # Charlie1, # Diana
])
代碼:
import numpy as np# 激活函數與激活函數的求導
def sigmoid(x):return 1/(1 + np.exp(-x))
def d_sigomid(x):return sigmoid(x) * (1 - sigmoid(x))# 神經元
class Neuron:'''-神經元基本屬性包括權重和偏置量-神經元方法前向計算和反向傳遞-神經元默認接收二維的輸入'''#初始化,針對特定尺寸的數據集def __init__(self):self.weights = np.random.normal(size=(1, 2))self.bias = np.random.normal()#前向計算過程集成化,用于訓練完成后一步輸出預測值def feedforward(self, inputs):Z = np.dot(self.weights, inputs) + self.biasreturn sigmoid(Z)#訓練函數def train_epoch(self, x_data, true_value):'''-迭代目的是更新權重參數和偏置參數,為了得到梯度需要知道導數為了計算導數需要知道前向計算過程中的一些值。訓練時按照這個思路去計算需要的值,再更新權重就可以。'''#準備工作learn_rate = 0.1epochs = 100for epoch in range(epoch):for x, y_true in zip(x_data, ture_value):#前向計算z = np.dot(self.weight, inputs) + self.biasy = sigmoid(z)#損失函數采用平方差計算,求導較為容易#l = (y - true_value) ** 2 #只有需要查看效果的輪次才計算輸出#一般只需要知道l關于y的導數即可,并不需要計算l的值#反向傳播d_L_d_y = -2 * (y_true - y)d_y_d_z = d_sigmod(z)d_z_d_w1 = x1 d_z_d_w2 = x2 #實際計算可以合并很多步驟,這里分開寫為了使過程更清晰dw1 = d_L_d_y * d_y_d_z * d_z_d_w1dw2 = d_L_d_y * d_y_d_z * d_z_d_w2db = d_L_d_y * d_y_d_z#體現了反向計算的復合過程#更新self.w[0] -= learn_rate * dw1self.w[1] -= learn_rate * dw2self.b -= learn_rate * dbif epoch % 10 == 0:if epoch % 10 == 0:y_preds = np.apply_along_axis(self.feedforward, 1, data)loss = ((y_preds - y_true) ** 2).mean()print("Epoch %d loss %.3f" % (epoch, loss))BPNN = Neuron()
BPNN.train(data, all_y_trues)
experiment
記錄1
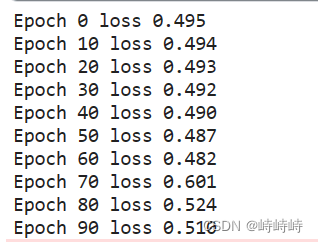

嘗試調參,沒有效果
嘗試輸出一些中間值,發現預測結果是沒問題的,只是loss的計算有問題
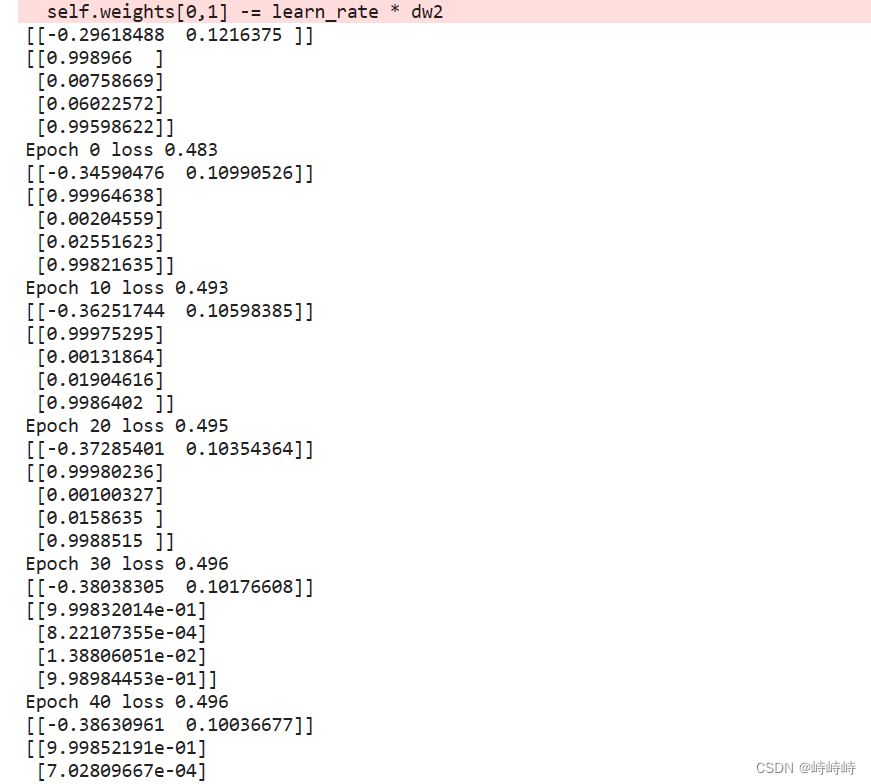
預測值是二維的列,真實值是一維的行,np廣播相減直接出來一個4*4的矩陣。做減法時加一個轉置就OK
記錄2
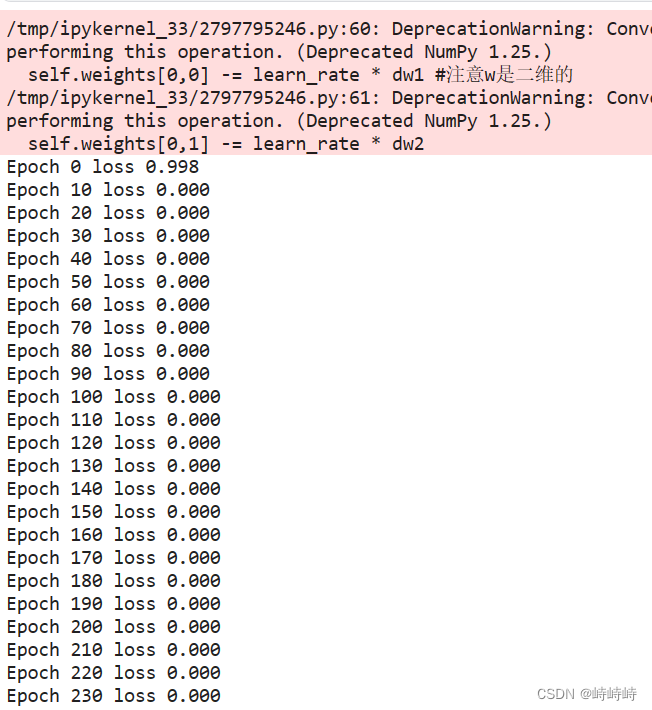
原因很明顯,問題過于簡單且沒有噪音。
增加了一些數據并加入少量噪音。
能明顯看到loss的下降過程,說明實驗成功。
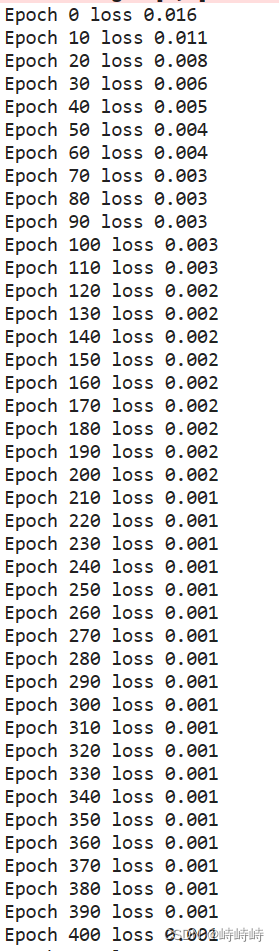
BPNN v-0.2向量化




)













)

