455 分發餅干

---------------🎈🎈題目鏈接🎈🎈-------------------

局部最優推全局最優：盡量用大餅干去滿足大胃口的小朋友

class Solution {public int findContentChildren(int[] g, int[] s) {// 貪心// 局部最優推全局最優：盡量用大餅干去滿足大胃口的小朋友if(s.length == 0) return 0;int result = 0;Arrays.sort(g);Arrays.sort(s);// 遍歷小孩胃口g[i]int start = s.length - 1;for(int i = g.length-1; i >=0; i--){if(start >= 0 && g[i] <= s[start]){result++;start--;}}return result;}
}  

時間復雜度：

對兩個數組進行排序的時間復雜度為 O(n log n)，其中 n 分別為小孩胃口數組 g 和餅干數組 s 的長度。
在最壞情況下，遍歷兩個數組的時間復雜度為 O(n)，其中 n 是小孩胃口數組 g 的長度。
因此，總的時間復雜度為 O(n log n)。

空間復雜度：

除了輸入數組 g 和 s 外，額外使用了常量空間進行迭代和計算。
因此，總的空間復雜度為 O(1)。

---

376. 擺動序列【規律很多】

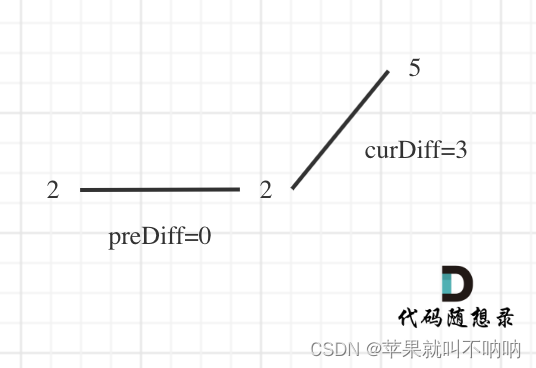
一正一負 找到一個峰值：(pre>=0 && cur<0) || (pre<=0 && cur>0)。result++，遇到波動點就更新pre的值為cur
設定開頭pre = 0：即原本是2-5，模擬為2-2-5 這樣可以保證計算到開頭的節點也算波動點。
設定開頭cur = 0 ，但是隨后循環中就賦值了 cur = nums[i+1] - nums[i]

思想：注意考慮一個坡度留首尾兩個點、平坡、首尾

class Solution {public int wiggleMaxLength(int[] nums) {
// 貪心  一個坡度上只留首位兩個點
// 考慮平坡的時候// 考慮單調有平坡 : 左右留一個就行 pre>=0 && cur<0 || pre<=0 && cur>0// 考慮上下中間有平坡 ：只需要在 坡度擺動變化的時候，更新 pre 就行，這樣 pre 在 單調區間有平坡的時候 就不會發生變化，造成我們的誤判
// 考慮首尾元素 首尾元素都要計算坡度 尾部直接result本身就為1，首部假定開頭pre=0int result = 1;int pre = 0; // 前一段默認先為0 后面遇到波動點的時候賦值為curint cur = 0;for(int i = 0; i < nums.length-1; i++){cur = nums[i+1] - nums[i];  // 后一段if((pre>=0 && cur<0) || (pre<=0 && cur>0)){  // 一正一負就找到一個峰值result++;pre = cur;  // 即出現波動點才給pre賦值為cur，就可以避免單調中平坡的影響} }return result;}
}

53. 最大子數組和【好思想】

題目鏈接

思想：遍歷nums，當前“連續和”為負數的時候立刻放棄，從下一個元素重新計算“連續和”

思想！！！：
如果一部分加和為負數，那么后面再加一個無論什么元素都相當于是減，那么就沒必要了
那么就遍歷nums，遇到和為負數就重新開始計算加和，
沒遇到的時候：如果加和結果大于result就給result賦值 最后返回result
注意這里用了int result = Integer.MIN_VALUE; 保證了若數組都為負數，result記錄的就是最大的負數。

class Solution {public int maxSubArray(int[] nums) {// 貪心算法，// 如果一部分加和為負數，那么后面再加一個無論什么元素都相當于是減，那么就沒必要了// 那么就遍歷nums，遇到和為負數就重新開始計算加和，沒遇到的時候如果加和結果大于result就給result賦值，// 最后返回resultint result = Integer.MIN_VALUE; // 這個很重要 可以保證如果全為負數的時候可以正常輸出int sum = 0;for(int i = 0; i < nums.length; i++){sum = sum+nums[i];if(sum > result) {  result = sum;}if(sum < 0){ // 如果加和小于零那就重新開始 因為后面再加沒必要了sum = 0;}    }return result; // 最后返回的result就是最大的}
}

---