粉刷房子

思路：

1.經驗+題目要求

dp[i][0] 表示：粉刷到 i 位置的時候，最后一個位置粉刷上紅色，此時的最小花費。
dp[i][1] 表示：粉刷到 i 位置的時候，最后一個位置粉刷上藍色，此時的最小花費。
dp[i][2] 表示：粉刷到 i 位置的時候，最后一個位置粉刷上綠色，此時的最小花費。

2.狀態轉移方程

因為相鄰兩個房子顏色不能相同，所以我們粉刷下一個位置只需要 找出上一個位置粉刷另外兩種顏色最小花費即可。
比如： i 位置是紅色，那么 i -1 只能是藍和綠 ，找出min(dp[i-1][1] , dp[i-1][2]);

3.
有 i -1 ，建表多建一行/一列，要求最小花費，初始化為0即可不影響填表

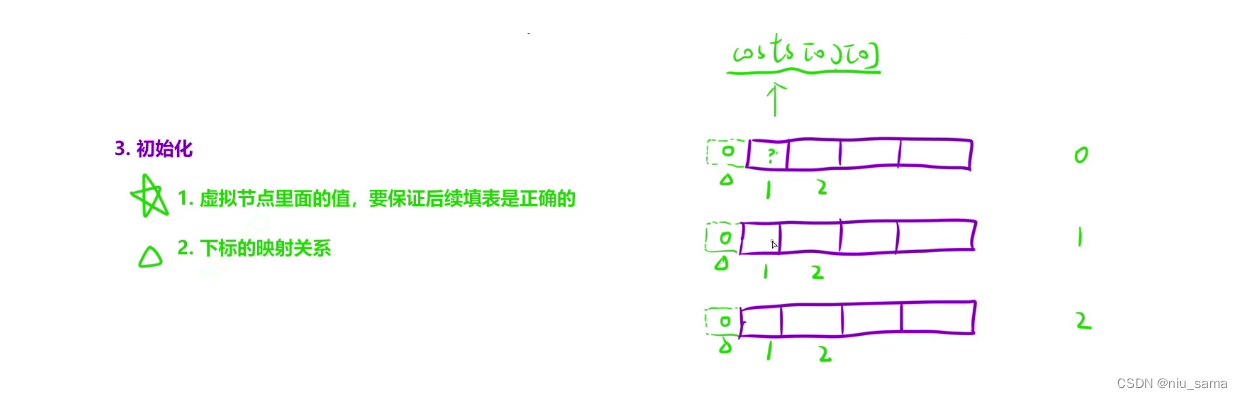
4 .
從左往右填表，一次填三個表

class Solution {
public:int minCost(vector<vector<int>>& costs) {int n = costs.size();vector<vector<int>> dp(n+1,vector<int>(3));for(int i = 1; i<=n; i++){dp[i][0] = min(dp[i-1][1],dp[i-1][2]) +costs[i-1][0];dp[i][1] = min(dp[i-1][0],dp[i-1][2]) +costs[i-1][1];dp[i][2] = min(dp[i-1][0],dp[i-1][1]) +costs[i-1][2];}return min(min(dp[n][0],dp[n][1]),dp[n][2]);}
};

買賣股票的最佳時機含冷凍期

思路：

1.經驗+題目要求

粉刷房子用顏色來表示的表，買賣股票可以用狀態表示。

dp[i][0] 表示：第 i 天結束以后，處于" 買入 " 狀態，此時的最大利潤。
dp[i][1] 表示：第 i 天結束以后，處于" 可交易 " 狀態，此時的最大利潤。
dp[i][2] 表示：第 i 天結束以后，處于" 冷凍期 " 狀態，此時的最大利潤。

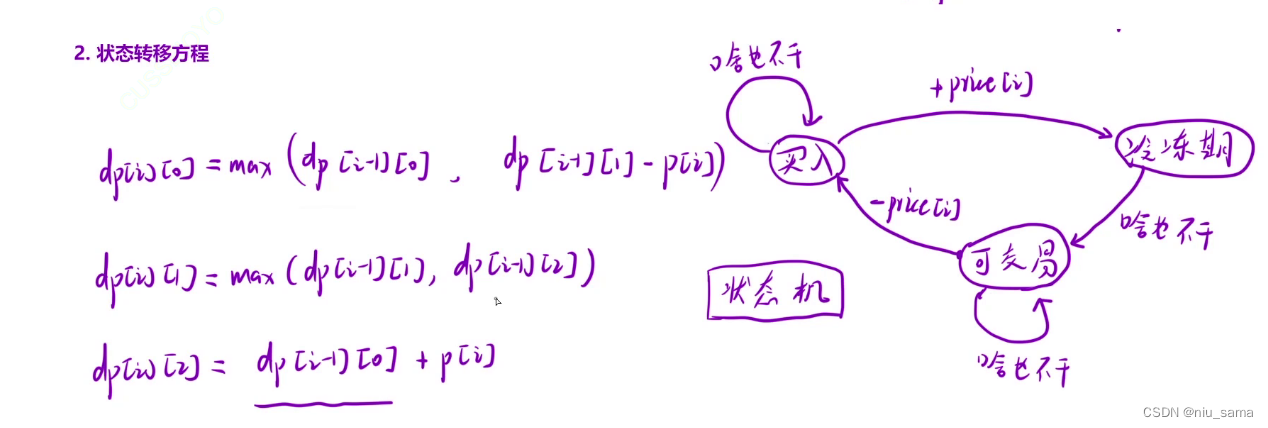
2.狀態轉移方程

每一個狀態都可以由 另一個狀態 轉變成：買入 可以 從買入，可交易轉換成。
例如： 買入 狀態可以 當天啥也不干還是買入，也可以從可交易狀態到買入，找出這兩個狀態的最大值即可。

3. 初始化

只有買入狀態的初始化，因為買入了所以為-p[0];

dp[0][0] = -p[0] , dp[0][1] = 0 , dp[0][2] = 0;

4.從左往右填寫，一次填寫三個表

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n+1,vector<int>(3));dp[0][0] = -prices[0];for(int i = 1; i<n; i++){dp[i][0] = max(dp[i-1][0],dp[i-1][1] - prices[i]);dp[i][1] = max(dp[i-1][1],dp[i-1][2]);dp[i][2] = dp[i-1][0] + prices[i];}return max(max(dp[n-1][0],dp[n-1][1]),dp[n-1][2]);}
};

買賣股票的最佳時機含手續費

思路：

1.經驗+題目要求

粉刷房子用顏色來表示的表，買賣股票可以用狀態表示。

f[i] 表示：第 i 天結束之后，處于"買入" 狀態，此時的最大利潤
g[i] 表示：第 i 天結束之后，處于"賣出" 狀態，此時的最大利潤

注意手續費的位置，手續費的位置在從買入到賣出狀態轉換的位置上。

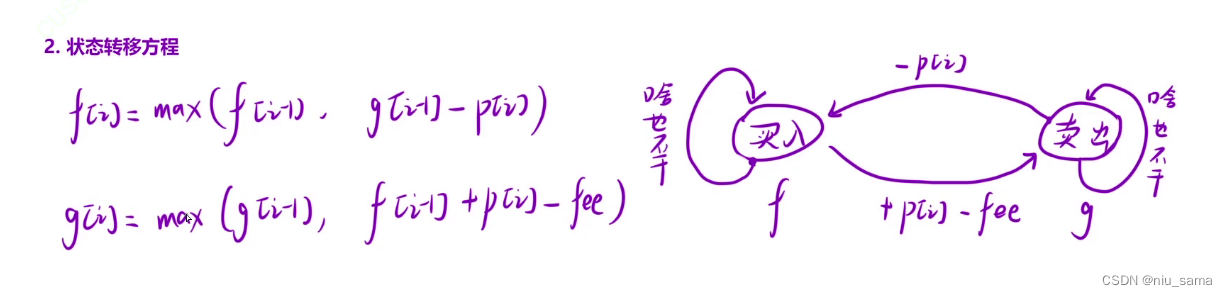
4.從左往右填寫，兩個表一起填

class Solution {
public:int maxProfit(vector<int>& prices, int fee) {int n = prices.size();vector<int> f(n);auto g = f;f[0] = -prices[0];for(int i = 1; i<n; i++){f[i] = max(f[i-1],g[i-1]- prices[i] );g[i] = max(g[i-1],f[i-1] + prices[i] -fee);}return max(f[n-1],g[n-1]);}
};

買賣股票的最佳時機 III

思路：

1.經驗+題目要求

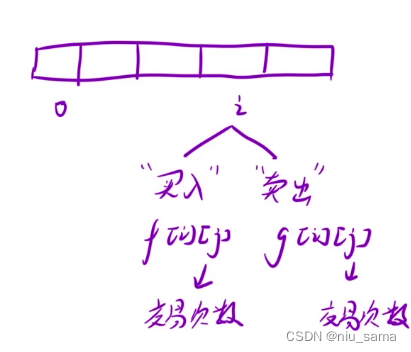
f[i][j] 表示：第 i 天結束之后，完成了 j 次交易，此時處于" 買入 " 狀態下的最大利潤
g[i][j] 表示：第 i 天結束之后，完成了 j 次交易，此時處于" 賣出 " 狀態下的最大利潤

狀態之間的轉換表達的狀態轉移方程和上面那幾道題一樣，但是，在判斷 g[i][j] 的時候，需要注意j-1，j-1需要額外判斷，
if(j-1) >=0 才能是 max狀態轉移方程，當j == 0時候，g[i][j] = g[i-1][j];

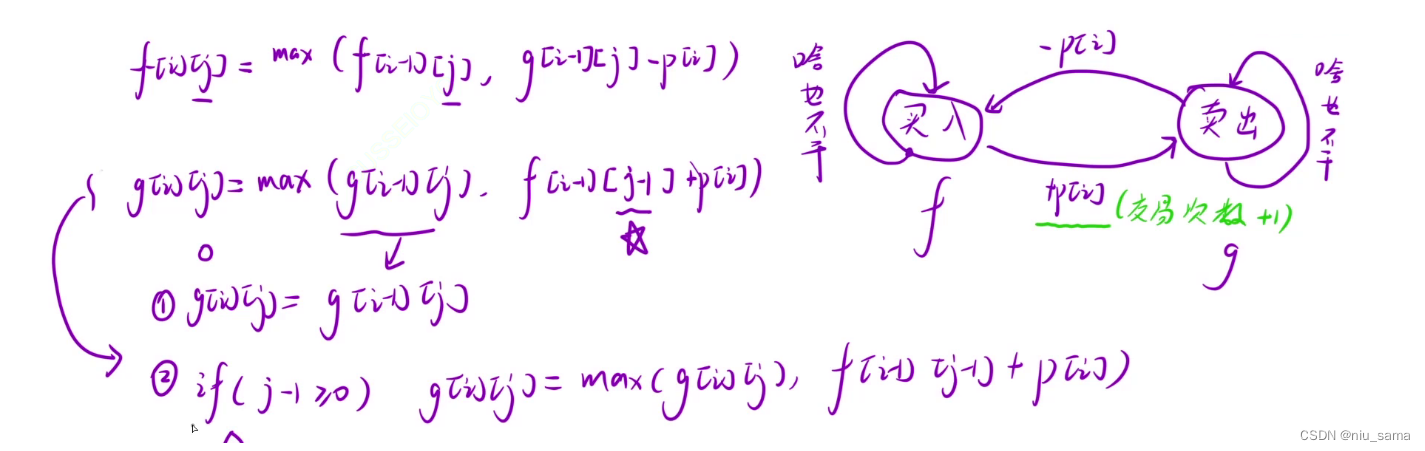
為了不影響max操作的比較，在第0天的時候，給第1和2次交易設為負無窮，但是又因為 上面 有g[i-1][j] - p[i] , 如果設為
INT_MIN ，就會超出范圍，所以設為 -0x3f3f3f3f 。

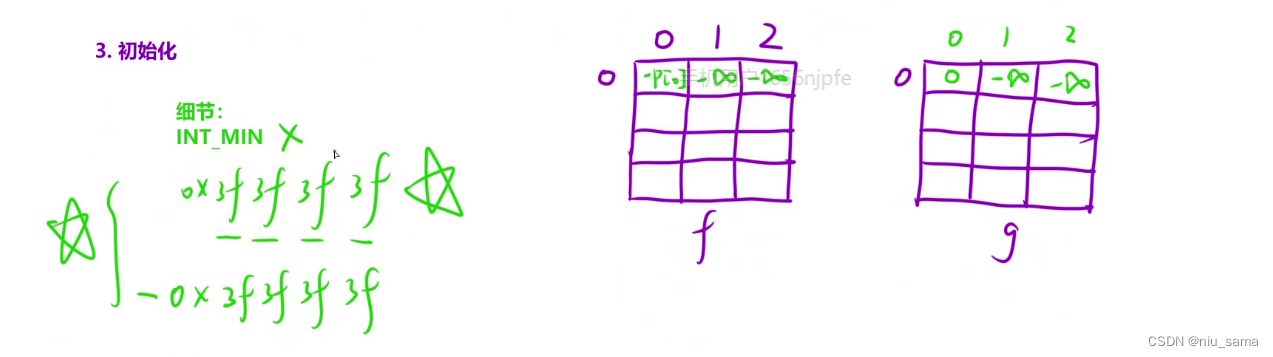
4.從上往下填寫每一行，兩個表一起填寫。

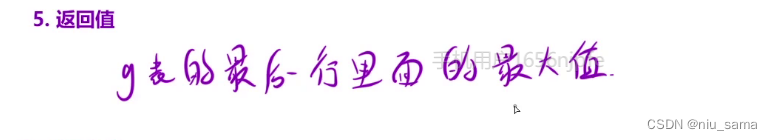
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> f(n,vector<int>(3));auto g = f;//f表初始化f[0][0] = -prices[0];for(int i = 1; i<3; i++){f[0][i] = -0x3f3f3f3f; //不能用INT_MIN,因為再+-都會超出極限g[0][i] = -0x3f3f3f3f;}//填表for(int i = 1; i<n; i++){for(int j = 0; j<3; j++){f[i][j] = max(f[i-1][j],g[i-1][j] - prices[i]);if(j-1 >=0)g[i][j] = max(g[i-1][j],f[i-1][j-1]+prices[i]);elseg[i][j] = g[i-1][j];}}int ret = 0;for(int i = 0; i<3; i++){ret = max(ret,g[n-1][i]);}return ret;}
};

買賣股票的最佳時機 IV

同 買賣股票的最佳時機 III，就留給練習上一題了。

class Solution {
public:int maxProfit(int k, vector<int>& prices) {int n = prices.size();vector<vector<int>> f(n,vector<int>(k+1));auto g = f;f[0][0] = -prices[0];for(int i = 1; i<k+1; i++){f[0][i] = -0x3f3f3f3f;g[0][i] = -0x3f3f3f3f;}for(int i = 1; i<n; i++){for(int j = 0; j<k+1; j++){f[i][j] = max(f[i-1][j],g[i-1][j] -prices[i]);if(j-1 >= 0)g[i][j] = max(g[i-1][j],f[i-1][j-1]+prices[i]);elseg[i][j] = g[i-1][j];}}int ret = 0;for(int i = 0; i<k+1; i++){ret = max(ret,g[n-1][i]);}return ret;}
};