●139.單詞拆分?

物品：wordDict里面的單詞；背包容量：s.size()。

1.dp[j]含義。dp[j]=true表示字符串前j個可以拆分成字典中的單詞。dp[s.size()] 就是最后的結果，整個字符串能（true）不能（false）拆分成字典中的單詞。

2.遞推公式。如leetcode，依次從l、le、lee、……、leetcode這8個字符串來檢查是否能拆分成字典中的單詞，最后返回 dp[s.size()] 這是外循環。然后對于每個字符串strj的檢查，如果這個單詞中有某個位置k為true（代表0到k這個位置可以拆分）且從k+1到這個單詞的結束位置j的子串（strj字符串剩下的子串）在wordDict里面，就說明這個字符串strj從0到j都能拆分，所以dp[j]更新為true，檢查這個位置k就得從字符串strj的開始到結尾了，取不取j都可以，這就是內循環。

所以這樣理解的話也確定了循環順序，外循環是背包（j從1到s.size()），內循環也是也是背包（i從0到 j-1），就跟以前做的題不太一樣。

3.初始化。dp[0]應該初始化為true，否則逐個判斷后面的元素不會得到true的值，其他的一開始就應該是false，然后后面再挨個更新，看是否換成false。

4.遍歷順序。根據之前的推理兩層循環都是背包，物品集合只是在循環里面做條件使用的。

5.打印。

代碼如下。

j=0初始為true，其他的初始為false，

class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {//物品：wordDict。//背包容量：svector<bool> dp(s.size()+1,false);  dp[0]=true;unordered_set<string> wordSet(wordDict.begin(),wordDict.end());for(int j=1;j<=s.size();++j){for(int i=0;i<j;++i){string sub=s.substr(i,j-i);if(wordSet.find(sub)!=wordSet.end() && dp[i]){dp[j]=true;}}}return dp[s.size()];}
};

●?關于多重背包，你該了解這些！?

多重背包問題：有N種物品和一個容量為V 的背包。第i種物品最多有Mi件可用，每件耗費的空間是Ci ，價值是Wi 。求解將哪些物品裝入背包可使這些物品的耗費的空間 總和不超過背包容量，且價值總和最大。

每件物品的最多Mi件可用，其實可以把Mi展開，就變成了01背包問題。

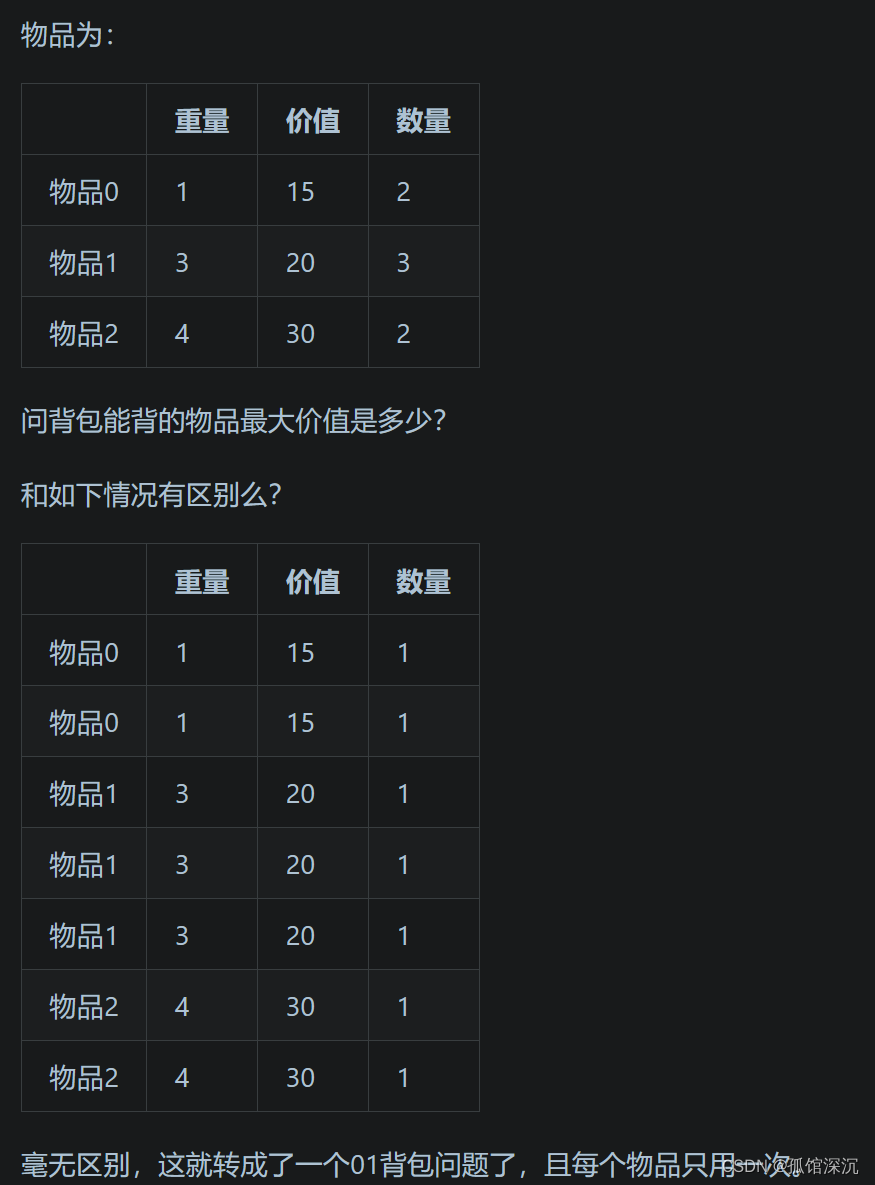
所以最直接的方法就是在重量數組和價值數組里面都把這些展開了的加入進去，物品0增加為2個……但是會超時。主要消耗在vector的動態底層擴容上。

 for (int i = 0; i < n; i++) {while (nums[i] > 1) { // 物品數量不是一的，都展開weight.push_back(weight[i]);value.push_back(value[i]);nums[i]--;}}

還有方法就是不改變這兩個數組，我們知道純01背包問題可以先物品，也可以先背包，然后考慮物品i放不放入兩種情況，01背包放入就只會放入一個，所以就一個遞推語句；但是多重背包可以放1個、……nums[i]個，所以每個物品i得有nums[i]個遞推。so解決純多重背包問題，要從純01背包問題的遞推代碼：

dp[j]=max(dp[j-weight[i]]+value[i],dp[j]]

改為：

for(int k=1;k<=nums[i];++k){if(j>=k*weight[i]){dp[j]=max(dp[j-k*weight[i]]+k*value[i],dp[j]);}
}

即每個物品，都考慮不放和放k個多種情況。

代碼如下：

#include<vector>
#include<iostream>
using namespace std;
void maxValue(){int begweight,N;cin >> begweight >> N;vector<int> dp(begweight+1,0);vector<int> nums(begweight+1);vector<int> weight(N);vector<int> value(N);for (int i = 0; i < N; i++) cin >> weight[i];for (int i = 0; i < N; i++) cin >> value[i];for (int i = 0; i < N; i++) cin >> nums[i];for(int i=0;i<N;++i){//先物品for(int j=begweight;j>=weight[i];--j){for(int k=1;k<=nums[i];++k){if(j>=k*weight[i])dp[j]=max(dp[j-k*weight[i]]+k*value[i],dp[j]);}}}cout<<dp[begweight];
}int main(){maxValue();return 0;
}

注意，在隨想錄中說：多重背包在面試中基本不會出現，力扣上也沒有對應的題目，大家對多重背包的掌握程度知道它是一種01背包，并能在01背包的基礎上寫出對應代碼就可以了。

●背包問題總結篇！?